Средства информационных и коммуникационных технологий. Логические функции и схемы – основа элементной базы компьютера

1.

3. Средства информационных
и коммуникационных
технологий

2.

3.3 Логические функции и
схемы – основа элементной
базы компьютера

3.

В жизни мы часто, сами того не замечая, используем логические
зависимости в самых разных ситуациях. Например, мы говорим:
«чтобы приготовить это блюдо, мне необходимо обязательно иметь
мясо, соус, соль и зелень» (перефразируя, можно сказать, что нужны
«И мясо, И соус, И соль, И зелень»). При этом подразумевается, что
отсутствие даже чего-либо одного из перечисленного не даст
возможности приготовить именно это блюдо. Другой пример:
направляясь в магазин, вы знаете, что можете доехать до него ИЛИ
на трамвае, ИЛИ на автобусе, ИЛИ на троллейбусе. В принципе, все
равно, на чем ехать, не устраивает только одна ситуация, при
которой не будет ни трамвая, ни автобуса, ни троллейбуса. Еще
пример: собираясь с друзьями в поход, вы предполагаете «надену
любую обувь, только НЕ эти кроссовки, поскольку они неудобны».

4.

А еще мы часто увязываем наступление или ненаступление каких
то событий в более сложные логические формы. Например, «я пойду
гулять, если успею выполнить домашние задания и если на улице не
будет дождя», «чтобы добраться до стадиона, нужно сначала ехать
на метро, а потом на автобусе или троллейбусе», «если в выходной
будет морозец, то я пойду с ребятами кататься на лыжах, иначе (т.е.
если будет слякоть) останусь дома и займусь компьютером».
Здесь мы привели простые, бытовые, но тем не менее, логические
зависимости. Несложно сообразить, что при обработке информации
такие зависимости возникают сплошь и рядом.

5.

Привычная алгебра оперирует числами, а алгебра логики –
событиями. Алгебру логики иначе называют булевой (в честь ее
создателя английского математика Джорджа Буля) или алгеброй
высказываний.
Любая формальная математическая система в общем случае
состоит из следующих основных множеств:
операндов (данных для обработки, или, иными словами,
информации);
операций (операторов или действий над информацией);
постулатов (законов, правил, теорем, аксиом, формул, по которым
осуществляется процесс обработки информации).

6.

Этому правилу подчиняется и алгебра логики. Рассмотрим
двузначный вариант алгебры логики, которая в качестве множества
элементов содержит два элемента «0» и «1». Будем называть их
константами алгебры логики, и, чтобы не путать с двоичными
цифрами, говорить о логическом «0» и логической «1». По причине
использования этих двух констант алгебру логики еще называют
переключательной алгеброй, поскольку типовой переключатель имеет
два фиксированных положения.
Условимся, что если некоторое событие А произошло, то это
записывается как А=1, а если оно не произошло, то А=0. В любом
случае
А = 0, если А ≠ 1; А = 1, если А ≠ 0.
Для обозначения событий или булевых переменных, используем
буквы латинского алфавита. Таким образом, мы определили множество
элементов алгебры логики.

7.

Рассмотрим наиболее распространенные логические операции.
Логическое умножение (конъюнкция) или операция И.
Давайте сначала попробуем разобраться, что называется «на
пальцах». Представьте себе елочную гирлянду из 10 лампочек, которые
включены последовательно. Если хотя бы одна лампочка перегорит,
то ток прекратится и гирлянда гореть не будет. Следовательно,
событие А (гирлянда горит) наступит тогда и только тогда, когда
произойдут события В1, В2, В3, ..., В10, где соответственно В1 –
исправность первой лампочки, В2 – второй и т.д. Сколько может быть
комбинаций различных состояний? Каждый элемент (лампочка)
может иметь два состояния (исправна – неисправна), а всего таких
элементов 10, следовательно, количество комбинаций определим как
210 = 1024.

8.

Иными словами, из 1024 комбинаций событий «исправна –
неисправна лампочка» только при одной комбинации, когда все
лампочки исправны, т.е. В1 = 1, В2 = 1, В3 = 1, ..., В10= 1, произойдет
событие А, т.е. А = 1, – гирлянда будет гореть. Во всех остальных
1023 случаях, если хотя бы одно из событий В1, В2, В3, ..., В10, не
наступит, т.е. будет равным 0, гирлянда гореть не будет, – событие
А не наступит, т.е. А = 0.
Пример. Урок информатики (событие S) состоится, если
произойдет событие А (пришла группа) и произойдет событие В
(пришел преподаватель). Очевидно, что S – это событие-функция,
наступление которого зависит от наступления событий А и В (событияаргументы). Сколько может быть комбинаций значений событий
аргументов и, соответственно, значений события-функции? Конечно,
четыре (см. таблицу).

9.

А
0 (класс не пришел)
0 (класс не пришел)
1 (класс пришел)
1 (класс пришел)
В
0 (преподаватель не пришел)
1(преподаватель пришел)
0 (преподаватель не пришел)
1(преподаватель пришел)
S
0 (урок не состоялся)
0 (урок не состоялся)
0 (урок не состоялся)
1 (урок состоялся)
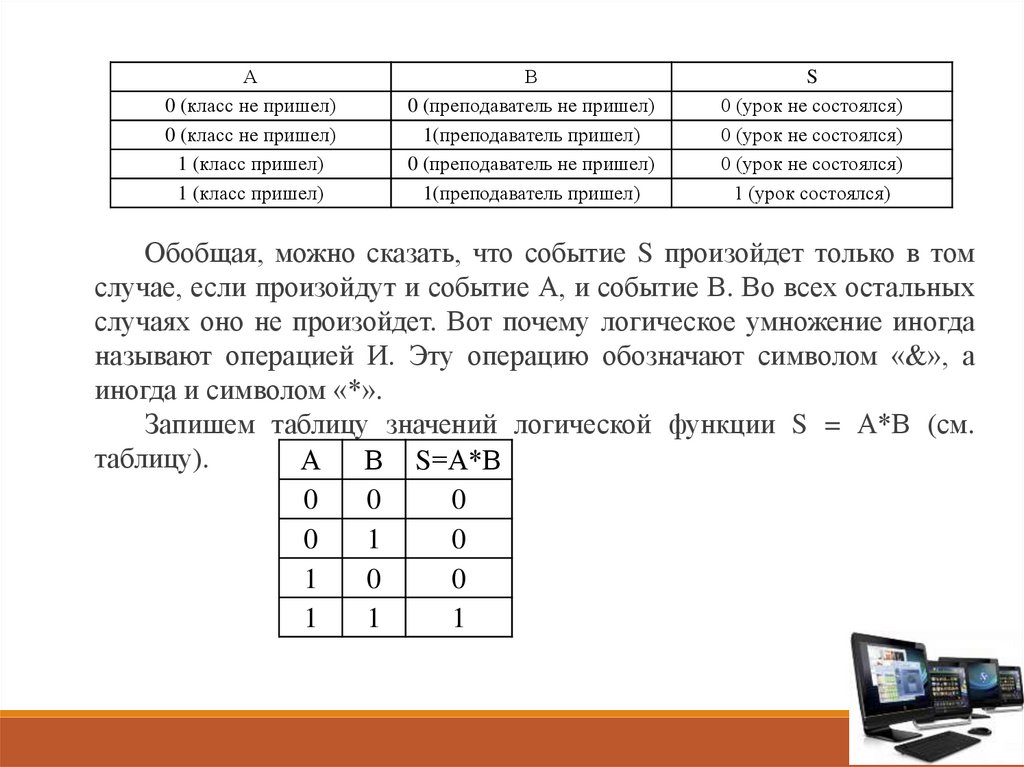
Обобщая, можно сказать, что событие S произойдет только в том
случае, если произойдут и событие А, и событие В. Во всех остальных
случаях оно не произойдет. Вот почему логическое умножение иногда
называют операцией И. Эту операцию обозначают символом «&», а
иногда и символом «*».
Запишем таблицу значений логической функции S = А*В (см.
таблицу).
А
В S=А*В
0
0
0
0
1
0
1
0
0
1
1
1

10.

Если мы рассмотрим логическое выражение А = В* С * D * Е * F,
то общее количество комбинаций значений логических операндов В, С,
D, Е, F будет равно 32, но только в одном случае, когда все они будут
равны 1, значение логической функции А будет 1, во всех остальных 31
случаях А = 0.
В конъюнктивных формах значение логической функции равно 1
только в одном случае – когда все логические операнды равны 1, во всех
остальных случаях значение логической функции равно 0. Эта
закономерность очень пригодится нам при упрощении сложных
логических выражений. Стоит убедиться, что один из операндов
конъюнктивной формы равен 0, и дальше можно не считать, а быть
уверенным, что и значение логической функции равно 0.

11.

Логическое сложение (дизъюнкция) или операция ИЛИ.
Рассмотрим пример. В вашей комнате висит светильник,
состоящий из трех лампочек, каждая из которых может включаться
отдельно. Когда произойдет событие S – в комнате горит свет?
Очевидно, тогда, когда будет гореть или одна лампочка, или любые
две, или все три. И только в одном случае из восьми (23= 8) событие S
не наступит – когда ни одна из лампочек гореть не будет.
Пример. Прогноз погоды, говорит: «Завтра возможны осадки».
Когда это событие будет истинным? Очевидно, что тогда, когда будет
идти снег или дождь или снег с дождем. И только в одном случае эго
событие не произойдет – когда ни снега, ни дождя, ни снега с дождем
не будет. Обозначим событие «выпадение осадков» как S, дождь – как
А, снег – как В. Комбинаций аргументов может быть четыре (22 = 4).
Событие S произойдет, если произойдет или событие А, или событие
В, или они оба. И только в одном случае событие S не произойдет
– когда не произойдет ни одно из событий аргументов
(см. таблицу).

12.

А
0 (дождь не идет)
0 (дождь не идет)
1 (дождь идет)
1 (дождь идет)
В
0 (снег не идет)
1(снег идет)
0 (снег не идет)
1(снег идет)
S
0 (осадков нет)
1 (осадки есть)
1 (осадки есть)
1 (осадки есть)
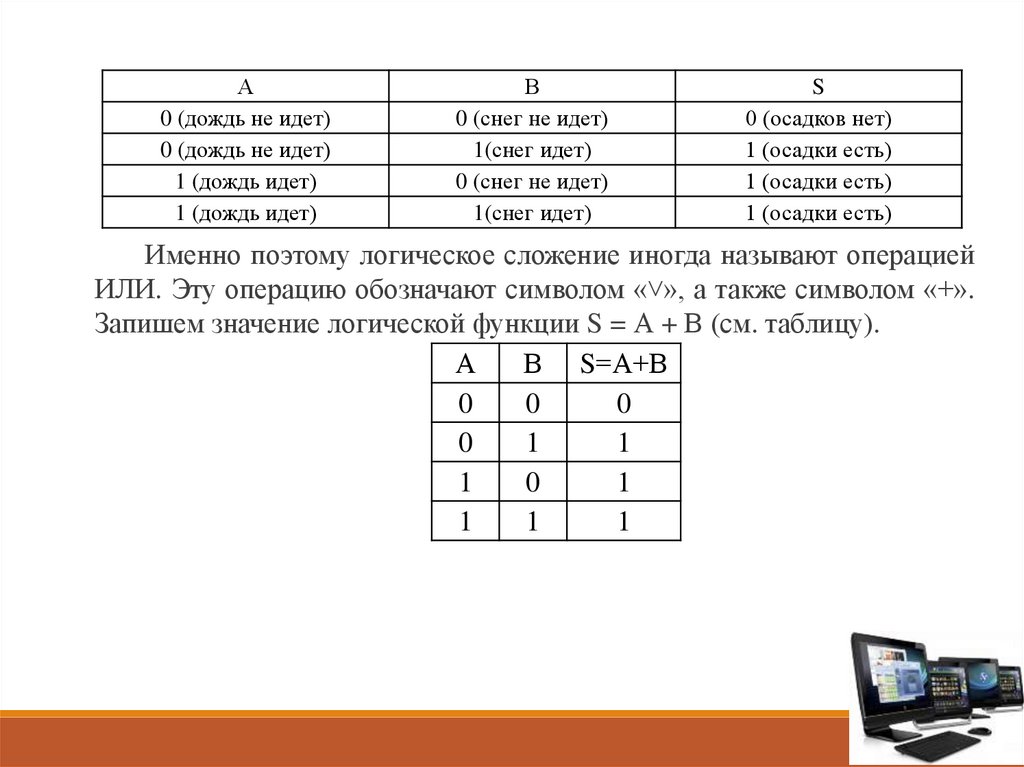
Именно поэтому логическое сложение иногда называют операцией
ИЛИ. Эту операцию обозначают символом «˅», а также символом «+».
Запишем значение логической функции S = А + В (см. таблицу).
А
В S=А+В
0
0
0
0
1
1
1
0
1
1
1
1

13.

Если же мы рассмотрим более сложную дизъюнктивную форму,
например: А = В + C + D + Е + F + G, то сразу определим, что
количество комбинаций значений логических операндов В, С, D, Е, F, G
будет равно 64, так как каждый операнд может иметь два значения,
а всего таких операндов шесть, причем в 63 случаях значение функции
будет равно 1 и только в одном 0. Попробуем обобщить.
В дизъюнктивных формах значение логической функции равно 0
только в одном случае – когда все логические операнды равны 0, во
всех остальных случаях значение логической функции равно 1. Эта
закономерность очень полезна при упрощении сложных логических
выражений. Действительно, стоит убедиться, что один из операндов
дизъюнктивной формы равен 1, как вывод очевиден – значение
логической функции равно 1.

14.

Логическое отрицание (инверсия) или операция НЕ. Смысл этой
функции заключается в том, что если значение логической переменной
есть А = 1, то значение ее отрицания есть А = 0, и наоборот (см.
таблицу).
А Ā
0 1
1 0
Логические схемы составляют основу построения многих
технических систем обработки информации, в том числе, конечно, и
компьютеров. Нас они будут интересовать как «черный ящик», т.е. нам
важно знать, что логические схемы получают на входе, и что – на
«выходе». Логические схемы выполняются, как правило, из диодов и
(или) транзисторов и их работа описывается алгеброй логики.

15.

На рисунке представлена логическая схема И (логическое
сложение, конъюнкция).
Схема имеет входы А и В и выход S. На вход подаются сигналы,
соответствующие значениям аргументов. Например, если А = 1, то на
входе А есть сигнал, если же В = 0, то на входе В сигнала нет.
Сигнал – это некое физическое воздействие на вход схемы. В
реальных схемах это, как правило, воздействие электрическим током
(напряжением). Очевидно, что приведенная логическая схема реализует
операцию S=А*В и будет работать в соответствии с приведенной ранее
таблицей значений, т. е. сигнал на выходе S будет только в том случае,
когда будут сигналы на входе А и на входе В, в остальных трех случаях
сигнала на выходе не будет, т. е. S = 0.

16.

Рассмотрим логическую схему ИЛИ (логическое сложение,
дизъюнкцию).
Схема имеет входы А и В и выход S. На вход подаются сигналы,
соответствующие значениям аргументов. Например, если А = 1, то на
входе А есть сигнал, если же В = 0, то на входе В сигнала нет.
Приведенная логическая схема реализует операцию S = А + В, она
будет работать в соответствии с приведенной ранее таблицей, т.е.
сигнал на выходе S будет тогда, когда на одном из входов А и В или же
на обоих будет сигнал. Когда же на входах не будет сигнала, его не
будет и на выходе S.

17.

Рассмотрим на примере логическую схему НЕ – это специальная
схема, которую будем называть схемой НЕ или инвертором.
Эта схема работает так, что если на входе есть сигнал, то на выходе
– нет, и наоборот, если сигнала нет на входе, то на выходе он есть.