Основы молекулярной физики. Лекция 7

1.

ОСНОВЫ МОЛЕКУЛЯРНОЙ ФИЗИКИ
1. Основные представления молекулярнокинетической теории и модель идеального
газа.
2. Изопроцессы и уравнение КлапейронаМенделеева.
3. Постоянная Больцмана, связь давления с
концентрацией и температурой.
4. Основное уравнение молекулярнокинетической теории. Среднеквадратичная
скорость.
1

2.

Статистический и термодинамический методы исследования
Молекулярная физика и термодинамика — изучают
макроскопические процессы в телах, связанные с огромным
числом содержащихся в них атомов и молекул. Для
исследования этих процессов применяют
два различных и дополняющих друг друга метода:
- статистический (молекулярно-кинетический)
- термодинамический.
Молекулярно-кинетические представления о строении и
свойствах вещества:
все тела состоят из молекул и атомов, находящихся в
непрерывном хаотическом движении.

3.

Процессы, изучаемые молекулярной физикой и
термодинамикой, являются результатом совокупного
действия огромного числа молекул.
(Число Лошмидта NL = 2,68· 1025 м-3 - это число
молекул, содержащихся в 1 м3 газа при нормальных
условиях)
Законы поведения огромного числа молекул, являясь
статистическими закономерностями, изучаются с
помощью статистического метода.
Макроскопические системы –
объекты с размерами от 10−7 м (100 нм) до 1012 м
3

4.

Свойства макроскопической системы определяются
свойствами частиц системы,
особенностями их движения,
усредненными значениями динамических характеристик
этих частиц (скорости, энергии и др.)
(агрегатные состояния вещества: Газ – Жидкость – Твердое тело)
Термодинамика — изучает общие свойства макроскопических
систем, находящихся в состоянии термодинамического
равновесия, и процессы перехода между этими состояниями
Термодинамическая система — совокупность макроскопических тел, которые взаимодействуют и обмениваются энергией
как между собой, так и с другими телами (внешней средой).
4

5.

Термодинамический метод. Задача — определение состояния
термодинамической системы.
Состояние системы задается термодинамическими
параметрами (параметрами состояния) —
совокупностью физических величин, характеризующих свойства
термодинамической системы.
Параметры состояния термодинамической системы температура Т,
давление р,
объем V
Задача молекулярной физики – установить связь между
микропараметрами и макропараметрами (p, V, T) системы.
5

6. Давление

p = F/S; S – площадь, на которую
действует сила F.
[p] = 1Н/1м2 = 1 Па (Паскаль)
S
Давление – скалярная величина,
численно равная силе, действующей на
единицу площади поверхности
Закон Паскаля: Давление передается
газом или жидкостью одинаково по всем
направлениям
6

7.

Температура — физическая величина, характеризующая
состояние термодинамического равновесия
макроскопической системы.
Две температурные шкалы
• термодинамическая - Кельвины (К);
• международная практическая - градусы Цельсия (°С).
Международная практическая шкала
(шкала Цельсия) - 2 реперные точки:
температура замерзания воды 0°С
температура кипения воды 100 °С
при давлении 1,013· 105 Па
(нормальное атмосферное давление)
7

8.

Термодинамическая температурная шкала определяется по
одной реперной точке:
тройная точка воды (температура, при которой лед, вода и
насыщенный пар при давлении 609 Па находятся в
термодинамическом равновесии).
Температура этой точки по термодинамической шкале равна
273,16 К (точно). 1 градус Цельсия равен 1 кельвину.
В термодинамической шкале температура замерзания воды
равна 273,15 К (при том же давлении, что и в Международной
практической шкале);
термодинамическая температура T и температура t по
Международной практической шкале связаны соотношением
T = 273,15 + t
Температура Т = 0 К называется нулем кельвин. Анализ
различных процессов показывает, что 0 К недостижим,
хотя приближение к нему сколь угодно близко возможно.
8

9.

Идеальный газ
В молекулярно-кинетической теории пользуются моделью
идеального газа:
1) собственный объем молекул газа пренебрежимо мал по
сравнению с объемом сосуда (молекулы – материальные
точки, не имеющие размера, но обладающие массой m);
2) между молекулами газа отсутствуют силы взаимодействия
(силы отталкивания или притяжения на расстоянии);
3) столкновения молекул газа между собой и со стенками
сосуда абсолютно упругие.
Наиболее близко свойствам идеального газа соответствуют
разреженные газы
9

10.

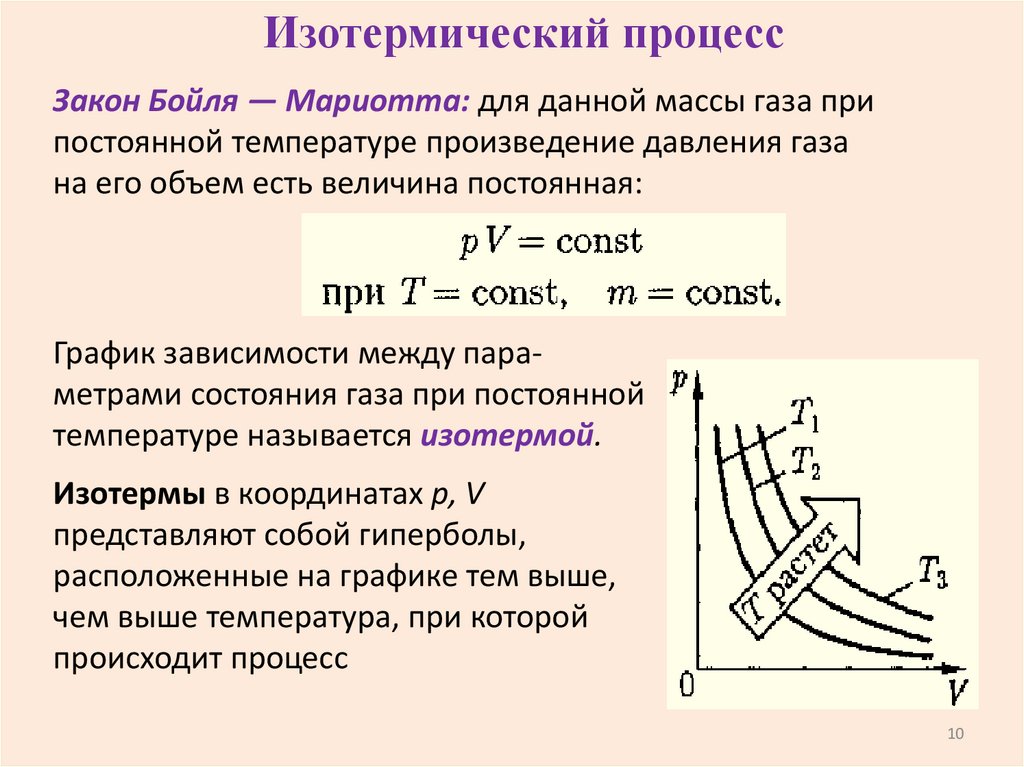
Изотермический процесс
Закон Бойля — Мариотта: для данной массы газа при
постоянной температуре произведение давления газа
на его объем есть величина постоянная:
График зависимости между параметрами состояния газа при постоянной
температуре называется изотермой.
Изотермы в координатах р, V
представляют собой гиперболы,
расположенные на графике тем выше,
чем выше температура, при которой
происходит процесс
10

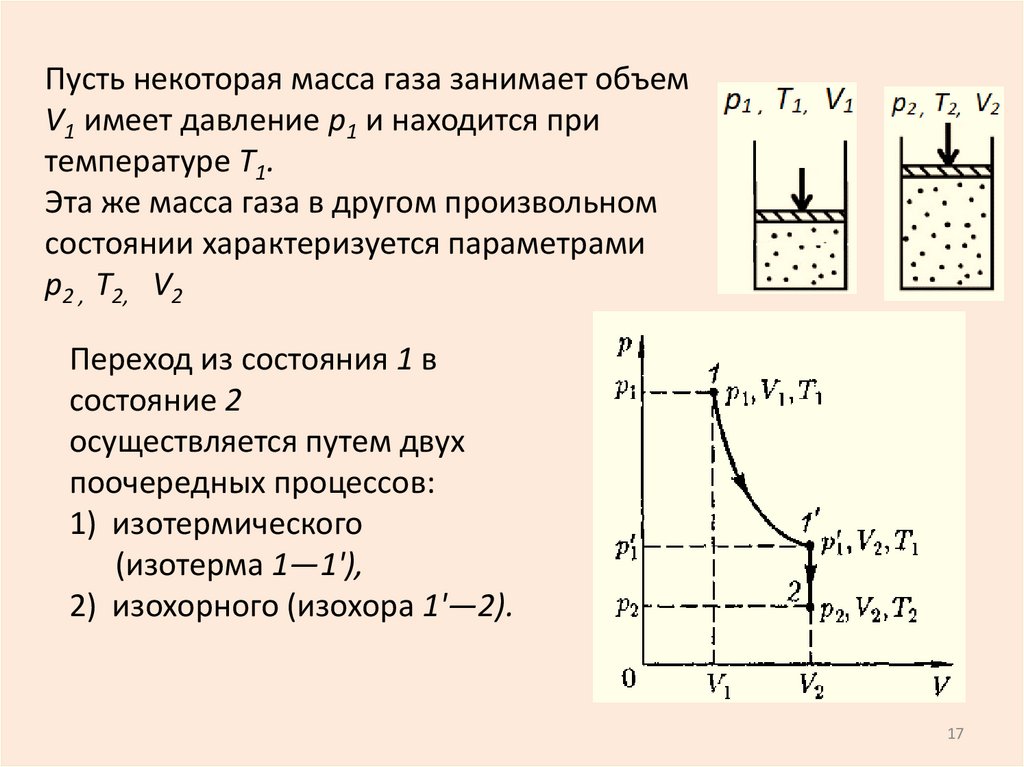
11.

Изобарный процесс
Закон Гей-Люссака: объем данной массы газа при постоянном
давлении изменяется линейно с температурой:
Процесс, протекающий при постоянном
давлении, называется изобарным. На
диаграмме в координатах V, t этот
процесс изображается прямой,
называемой изобарой
t — температура по шкале Цельсия,
Vo —объем при 0°С, коэффициент
α = 1/273,15 К- 1
11

12.

Изохорный процесс
Закон Шарля: давление данной массы газа при постоянном
объеме изменяется линейно с температурой
Процесс, протекающий при
постоянном объеме,
называется изохорным. На
диаграмме в координатах р, t он
изображается прямой, называемой
изохорой.
t — температура по шкале
Цельсия, рo— давление при 0°С,
коэффициент α = 1/273,15 К- 1
12

13.

α = 1/273,15
1+ αt = αT
T = 273,15 + t
Закон Гей-Люссака
Закон Шарля
V = Vo(1+ αt) = VoαT
p = рo(1+ αt) = рoαT