Дисперсионный анализ. Лекция 8

1. Лекция № 8. Дисперсионный анализ

2. Основные определения дисперсионного анализа

Дисперсионный анализ – это метод комплексной оценки сравниваемых средних нескольких
генеральных совокупностей.
Пусть изучается влияние некоторого фактора (одного или нескольких) на параметр-отклик.
Изучаемый фактор называется контролируемым фактором и разбивается на несколько градаций. Тогда
каждой градации контролируемого фактора будет соответствовать своя генеральная совокупность.
Ставится задача комплексного сравнения средних полученных генеральных совокупностей без
использования их попарного сравнения.
Сущность дисперсионного анализа состоит в разложении дисперсии параметра-отклика на
составляющие:
дисперсию вследствие влияния контролируемых факторов;
дисперсию, вызываемую действием неконтролируемых, случайных факторов и ошибками
измерений.
По доле дисперсии, обусловленной контролируемыми факторами, определяется степень и
значимость влияния факторов на параметр-отклик.
В зависимости от количества контролируемых факторов различают одно- двух- и
многофакторный дисперсионный анализ. Каждый контролируемый фактор может фиксироваться на двух,
трех и более градациях. Моделируемый параметр-отклик оценивается количественно по интервальной
или порядковой шкале для каждого сочетания градаций факторов.
Правильное применение дисперсионного анализа требует, чтобы изучаемые генеральные
совокупности имели нормальное или близкое к нормальному распределению, при этом дисперсии
сравниваемых групп не должны сильно различаться.

3. Однофакторный дисперсионный анализ

Процедура дисперсионного анализа однофакторных комплексов
состоит из следующих шагов:
1.
Группируют экспериментальные данные в виде таблицы, где
каждый столбец (или строка) соответствует градации контролируемого
фактора.
2.
Вводят обозначения:
N – общее число наблюдений,
a – число градаций контролируемого фактора,
ni – число наблюдений в градации i, i=1, …, a,
xi – значение параметра отклика, i=1, …, N.
3.
Рассчитывают девиаты
где Dy – общая, DA – межгрупповая, De – внутригрупповая девиаты.

4. Продолжение…

4.
5.
Определяют степени свободы:
ky=N-1 для общего варьирования,
kA=a-1 для факториального варьирования,
ke=N-a для остаточной дисперсии.
Определяют дисперсии:
Sy2 = Dy/ky, SA2 = DA/kA, Se2 = De/ke,
где Sy2 – общая, SA2 – межгрупповая, Se2 – внутригрупповая дисперсии.
6.
Вычисляют отношение межгрупповой дисперсии к внутригрупповой,
которое служит критерием оценки влияния регулируемых в эксперименте
факторов на параметр-отклик, т.е.
Fф=SA2/ Se2.
7.
Нулевая гипотеза исходит из предположения, что различия между
групповыми средними вызваны случайными факторами. Нулевая гипотеза
отвергается, если Fф>Fst для принятого уровня значимости и числа степеней
свободы kA и ke.

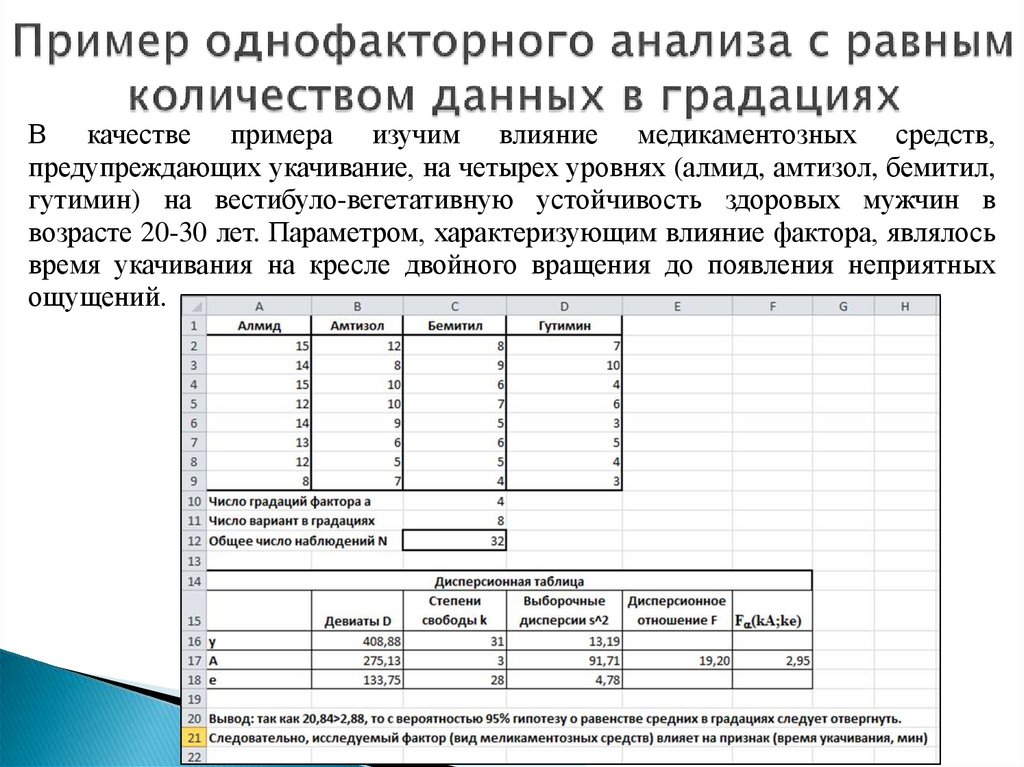
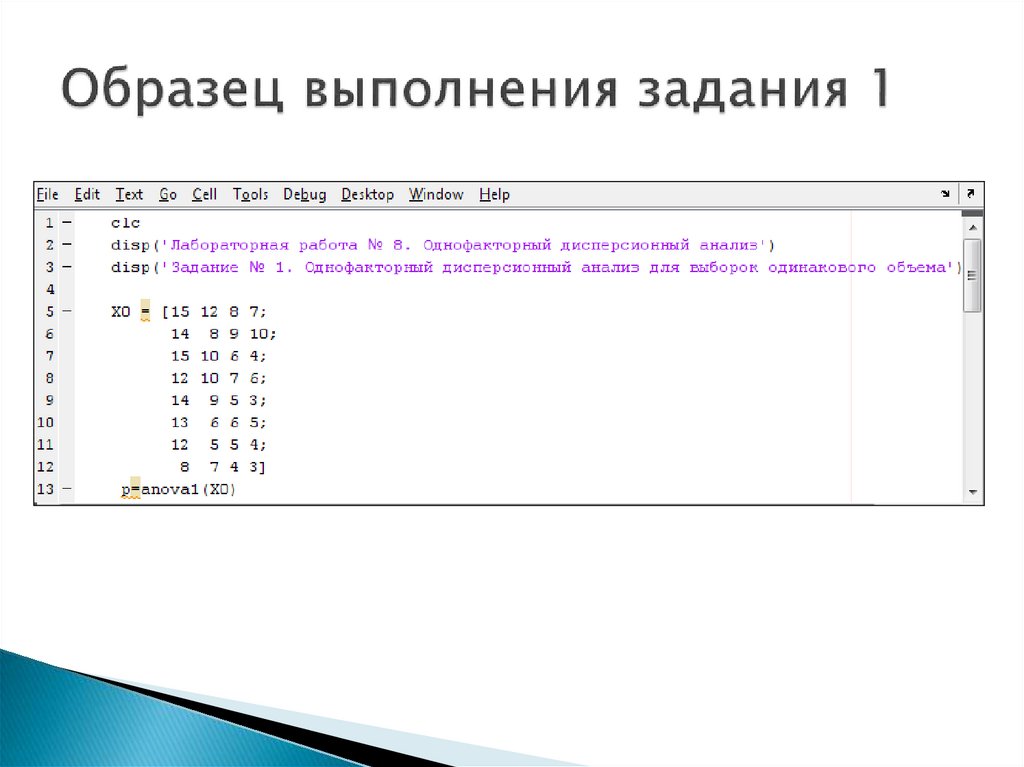
5. Пример однофакторного анализа с равным количеством данных в градациях

В качестве примера изучим влияние медикаментозных средств,
предупреждающих укачивание, на четырех уровнях (алмид, амтизол, бемитил,
гутимин) на вестибуло-вегетативную устойчивость здоровых мужчин в
возрасте 20-30 лет. Параметром, характеризующим влияние фактора, являлось
время укачивания на кресле двойного вращения до появления неприятных
ощущений.

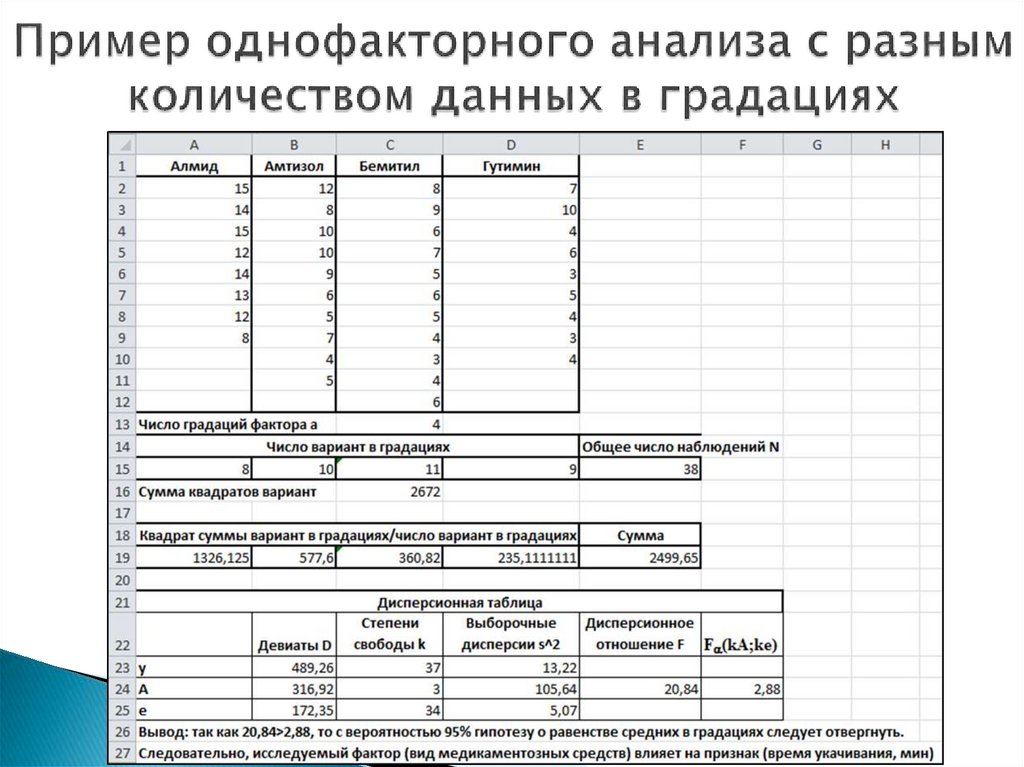
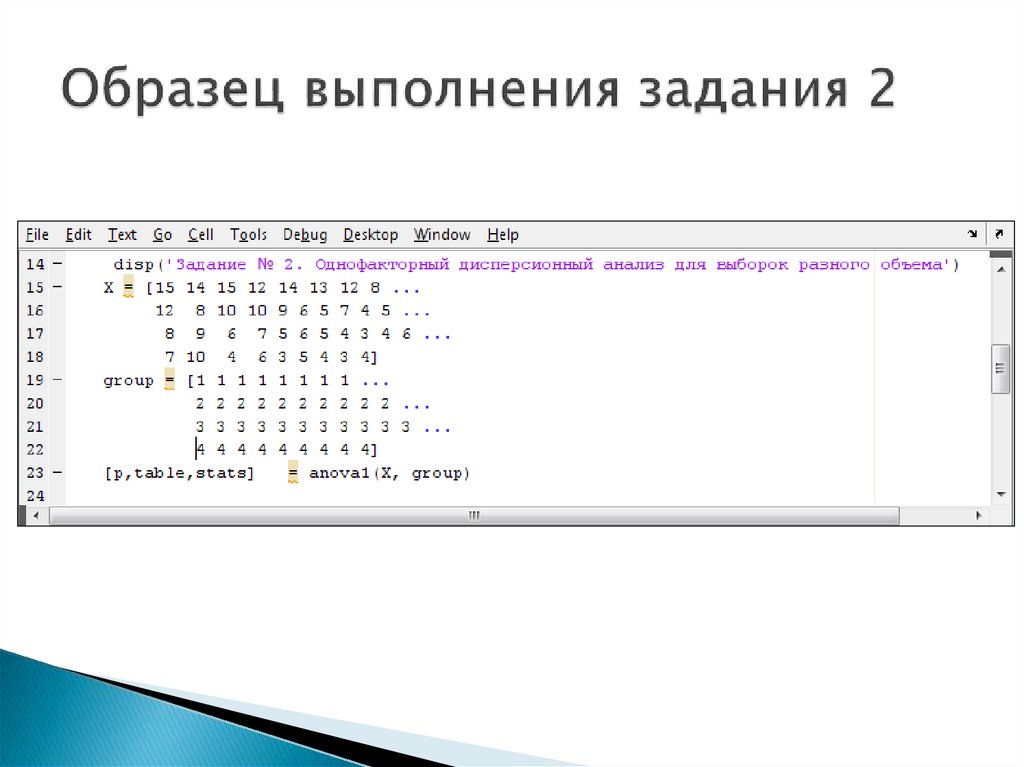
6. Пример однофакторного анализа с разным количеством данных в градациях

7. Функции MATLAB для выполнения заданий

o
o
o
o
o
anova1()
Варианты функции:
p=anova1(X)
p=anova1(X,group)
p=anova1(X,group,'displayopt')
[p,table]=anova1(...)
[p,table,stats]=anova1(...)

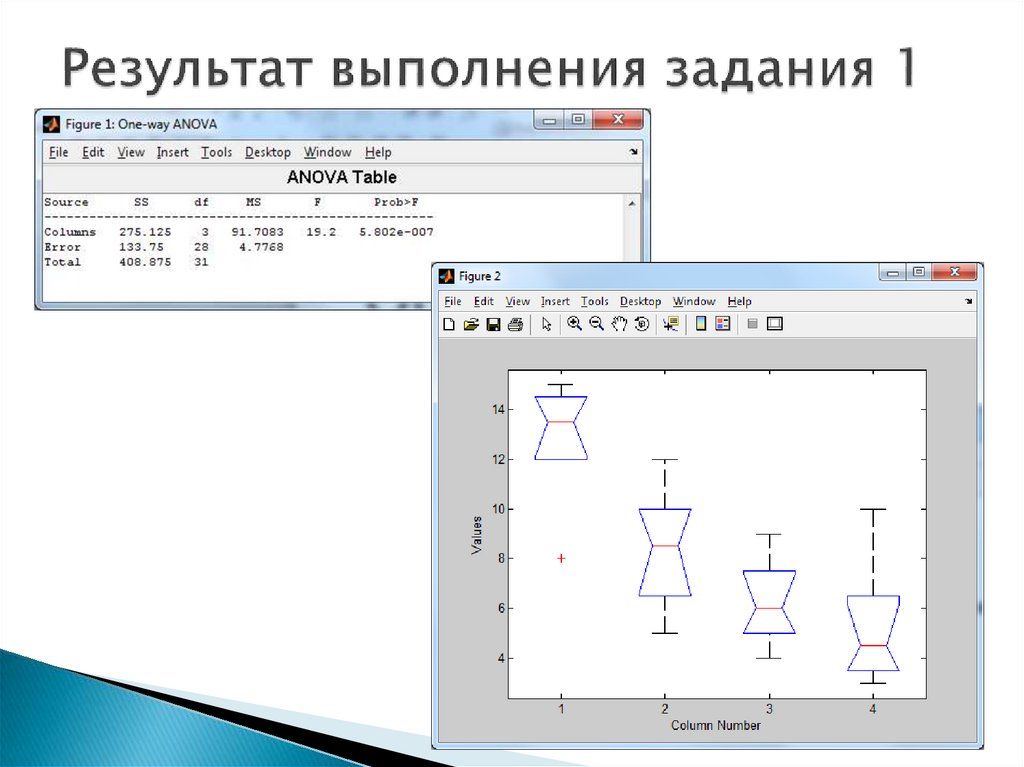
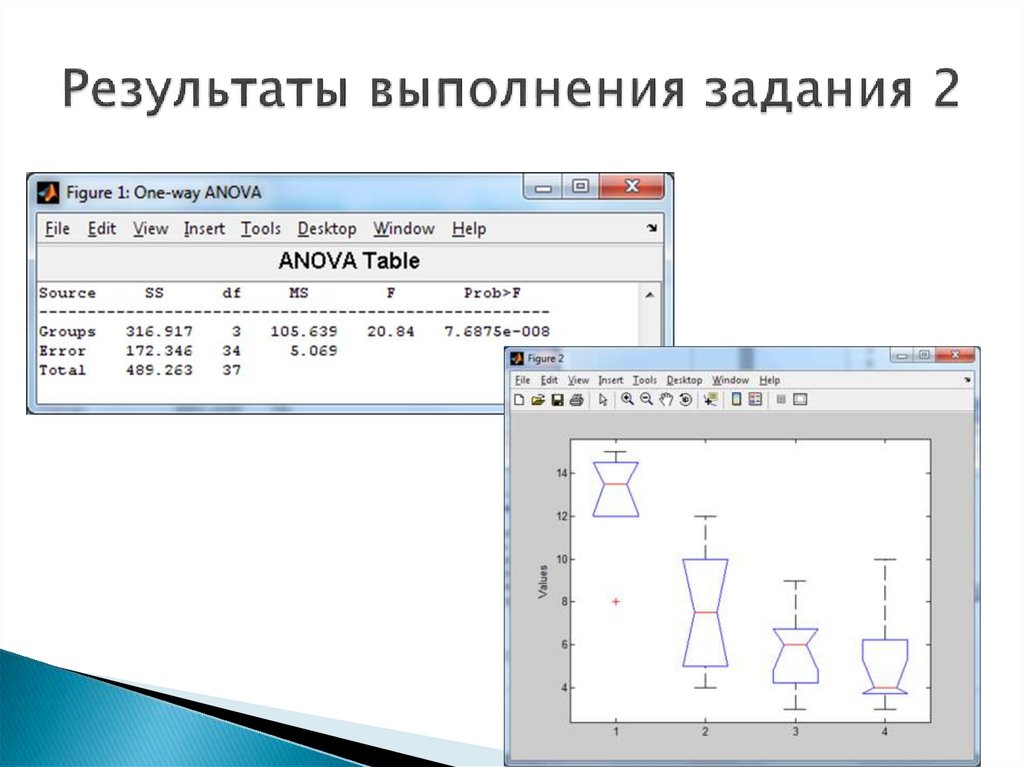
8. Результаты расчета функции anova1()

Результаты расчета отображаются в двух графических окнах:
в первое окно выводится таблица с результатами однофакторного
дисперсионного анализа,
во второе – диаграмма размаха для средних арифметических по заданным
выборкам.
Таблица с результатами содержит:
вид дисперсии (Source):
◦
внутригрупповая (Columns),
◦
межгрупповая (Error),
◦
общая (Total);
сумму квадратов разностей (SS) между средним арифметическим и
значениями выборки по каждому виду дисперсии;
число степеней свободы по каждому виду дисперсии (df);
среднее значение суммы квадратов разностей (MS) по каждому виду
дисперсии, определяемое как отношение SS/df;
значение статистики Фишера (F статистики) для MS;
значение уровня значимости p для рассчитанного значения статистики F.

9. Входной аргумент group

p = anova1(X, group)

10. Другие варианты функции

p=anova1(X,group,'displayopt')
'displayopt'='on', 'displayopt'='off'.
Значение по умолчанию 'displayopt'='on'.
[p,table]=anova1(...)
[p,table,stats]=anova1(...)
Структура данных stats передается
multcompare как входной аргумент.
функции

11. Функция multcompare()

c = multcompare(stats)
Функция
предназначена
проверки
параметрических гипотез при парном сравнении
средних арифметических или других оценок на
основе информации в структуре данных stats.
Выходным параметром является матрица с
результатами проверки параметрических гипотез.
Также
функция
позволяет
построить
интерактивный график по результатам проверки
множества параметрических гипотез.

12. Функция multcompare()

Для попарного сравнения средних используется функция
multcompare()
Варианты функции:
o c = multcompare(stats)
o c = multcompare(stats,alpha)
o c = multcompare(stats,alpha,'displayopt')
o c = multcompare(stats,alpha,'displayopt','ctype')
o c = multcompare(stats,alpha,'displayopt','ctype','estimate')
o c = multcompare(stats,alpha,'displayopt','ctype','estimate',dim)
o [c,m] = multcompare(...)
o [c,m,h] = multcompare(...)

13. Выходной параметр c

Выходной параметр с представляет результаты множественного
сравнения в виде матрицы из 5 столбцов. Строка матрицы с
соответствуют результатам проверки одной параметрической гипотезы.
Таким образом, каждая строка с соответствует одной паре выборок.
Первые два значения в строке с показывают номера сравниваемых
выборок, третий - величину разности средних арифметических
сравниваемых выборок, четвертый и пятый столбцы - 95%
доверительный интервал полученной разности средних арифметических.
Например, если строка с содержит следующие значения:
2.0000 5.0000 1.9442 8.2206 14.4971,
то полученные значения показывают, что сравниваются средние
арифметические значения 2 и 5 выборок, величина их разности равна
1.9442, 95% доверительный интервал полученной разности средних
арифметических составил [1.9442, 14.4971]. Поскольку в доверительный
интервал не попало нулевое значение, следовательно разность средних
арифметических 2 и 5 выборок значима, т.е. средние арифметические
выборок статистически значимо отличаются друг от друга, для aкр=0,05.

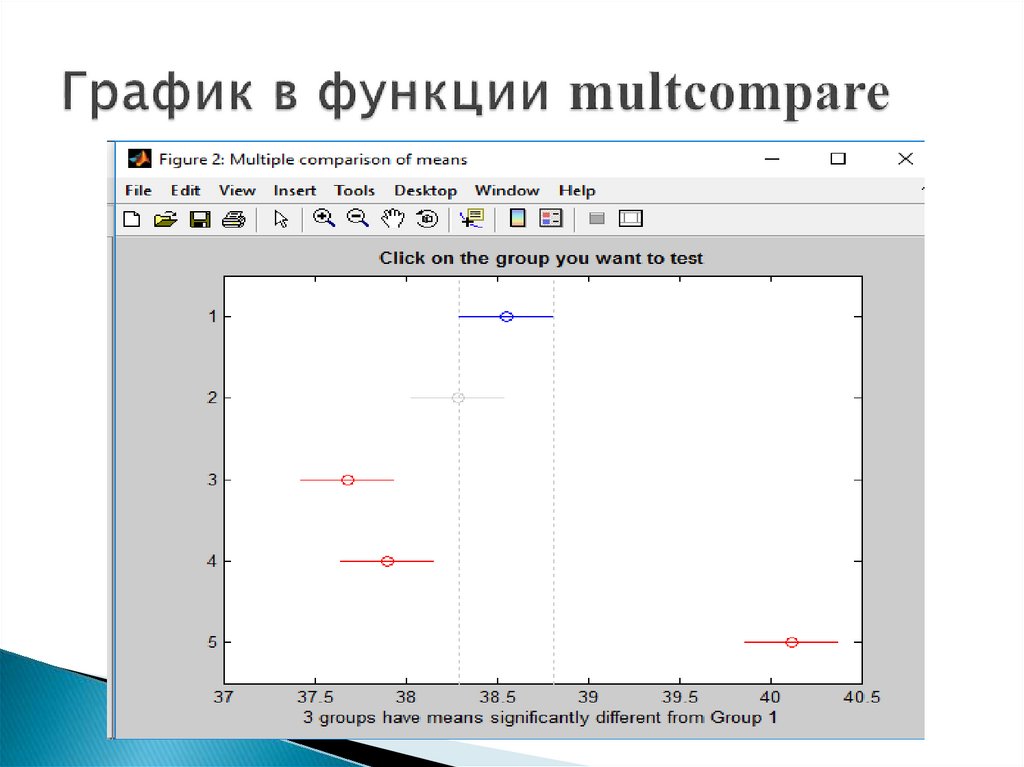
14. График в функции multcompare

15. Задания к лабораторной работе

Задание 1
Выполнить однофакторный дисперсионный анализ для
выборок, имеющих равное количество значений; провести
попарное сравнение средних.
Задание 2
Выполнить однофакторный дисперсионный анализ для
выборок, имеющих различное количество значений; провести
попарное сравнение средних.
Задание 3
Выполнить
однофакторный
дисперсионный
анализ
генеральной совокупности, имеющей равное и разное
количество значений, на языке программирования.