Similar presentations:
Однородные тригонометрические уравнения
1. Однородные тригонометрические уравнения
2.
a sin x + b cos x = 0— однородное
тригонометрическое уравнение
первой степени
(а≠0, b≠0)
a sin2 x + b sin x cos x + c cos2 x = 0
— однородное
тригонометричеcкое уравнение
второй степени
3. Алгоритм решения однородного тригонометрического уравнения первой степени
a sin x + b cos x = 0sin x
cos x
0
a
b
cos x
cos x cos x
a tg x + b = 0
b
tg x
a
Разделим обе части почленно на cos x
≠ 0 (если cos x = 0, то и sin x = 0, что
противоречит основному
тригонометрическому тождеству)
(то есть значения x,
при которых cos x = 0, не являются
корнями данного уравнения)
4. Алгоритм решения полного однородного тригонометрического уравнения второй степени (т.е. если а ≠ 0, b ≠ 0, с ≠ 0)
a sin2 x + b sin x cos x + c cos2 x = 0sin 2 x
sin x cos x
cos 2 x
0
a
b
c
2
2
cos x
cos x cos x
cos x cos 2 x
a tg2x + b tg x + c = 0
Разделим обе части почленно на
cos2 x ≠ 0 (если cos x = 0, то и
sin x = 0, что противоречит
основному
тригонометрическому
тождеству)
(то есть значения x,
при которых cos x = 0, не
являются корнями данного
уравнения)
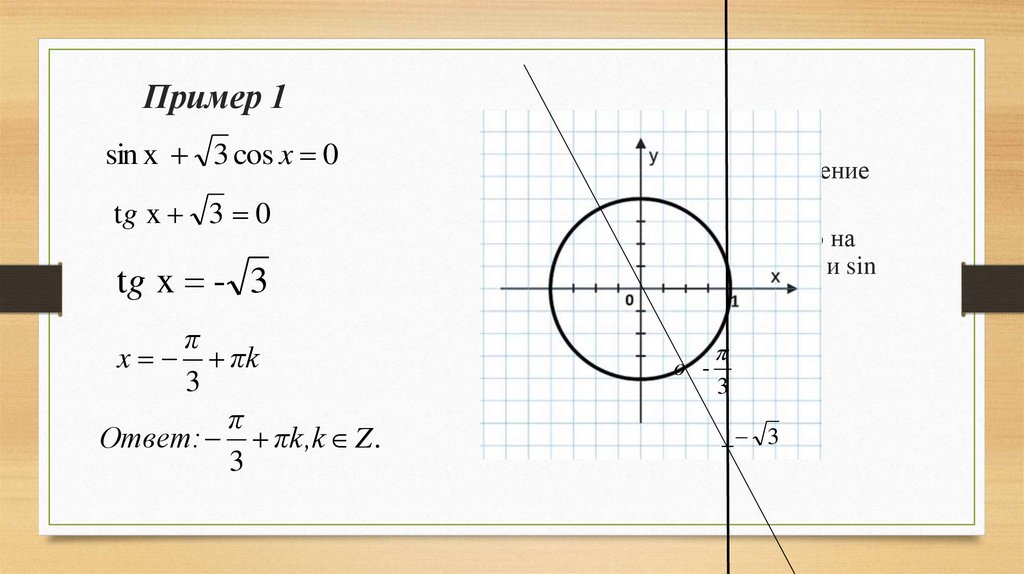
5. Пример 1
sin x 3 cos x 0tg x 3 0
tg x - 3
π
x πk
3
π
Ответ: πk,k Z .
3
— однородное
тригонометрическое уравнение
первой степени
Разделим обе части почленно на
cos x ≠ 0 (если cos x = 0, то и sin
x = 0, что противоречит
основному
тригонометрическому
тождеству) о - 3
_ 3
6. Пример 2
sin2 x+ sin x cos x = 0
sin x (sin x + cos x) = 0
sin x = 0 или sin x + cos x = 0
x = πk
tg x = -1
π
x πk
4
π
Ответ: k , πk,k Z.
4
— неполное однородное
тригонометрическое уравнение второй
степени
— однородное тригонометрическое
уравнение первой степени
Разделим обе части почленно на cos x ≠ 0
(если cos x = 0, то и sin x = 0, что
противоречит основному
тригонометрическому тождеству)
7. Пример 3
— полное однородноеsin2x + 2 sin x cos x – 3cos2 x = 0
тригонометрическое уравнение
2
tg x + 2 tg x – 3 = 0
второй степени
Пусть t = tg x
Разделим обе части почленно на
2
t + 2t – 3 = 0
cos2 x ≠ 0 (если cos x = 0, то и
sin x = 0, что противоречит
D = 16, t1 = – 3, t2 = 1
основному
Вернёмся к переменной x:
тригонометрическому
tg x = -3
или tg x = 1
тождеству)
π
x = - arctg 3 + πk
x πk
4
π
Ответ: arctg 3 πk, πk,k Z .
4
8. Пример 4
5sin2x - 14 sin x cos x – 3cos2 x = 25sin2x - 14 sin x cos x – 3cos2x - 2cos2x -2sin2x = 0
3sin2x - 14 sin x cos x – 5cos2x = 0 — полное однородное тригонометрическое
уравнение второй степени
3tg2x - 14 tg x – 5 = 0
2x≠0
Разделим
обе
части
почленно
на
cos
Пусть t = tg x
(если cos x = 0, то и sin x = 0, что
2
3t - 14t – 5 = 0
противоречит основному
тригонометрическому тождеству)
D = 256, t1 = – 1/3, t2 = 5
Вернёмся к переменной x:
tg x = -1/3
или
tg x = 5
x = - arctg 1/3 + πk
x = arctg 5 + πk
Ответ: - arctg 1/3 + πk, arctg 5 + πk, k€Z.







 mathematics
mathematics








