Одномерные распределения. Лекция 2

1. Лекция № 2. Одномерные распределения

2. Дискретные распределения

Биноминальное распределение
Случайная величина X называется распределенной по
биномиальному закону с параметрами N>0, p (0,1) если ее
возможные значения равны 0, 1, 2,…, N, а соответствующие
вероятности определяются формулой
Распределение Пуассона
Случайная величина X называется распределенной по закону
Пуассона с параметром a>0, если ее возможные значения
равны 0, 1, 2,…, а соответствующие вероятности
определяются формулой

3. Непрерывные распределения

Равномерное распределение на отрезке R(a,b)
Случайная величина непрерывного типа X
называется распределенной равномерно на отрезке
[a,b], если ее плотность распределения вероятностей
постоянна на данном отрезке:
Функция распределения определяется формулой:

4. Непрерывные распределения

Экспоненциальное распределение Ex(a)
Случайная величина непрерывного типа X
называется распределенной по показательному
(экспоненциальному) закону с параметром a>0, если
ее плотность распределения вероятностей задается
формулой
Функция распределения определяется формулой

5. Непрерывные распределения

Нормальное распределение N(a,s)
Нормальное распределение N(a,s) – одно из самых
распространенных в статистической практике.
Нормальное распределение с параметрами a=0 и s=1
называется стандартным.
Плотность вероятности для N(0,1) и N(a,s) задается
соответственно формулами:

6. Непрерывные распределения

Функция распределения для N(0,1) и N(a,s) задается
соответственно :
Вероятность того, что случайная величина X,
имеющая нормальное распределение
N(a,s),
попадает в интервал (x1, x2) определяется формулой

7. Непрерывные распределения

Распределение 2
Распределением 2 с k степенями свободы называется
распределение случайной величины 2(k), равной сумме
квадратов k независимых нормально распределенных по
закону N(0,1) случайных величин Ui, i=1, 2, …, k, т.е.
распределение случайной величины
2(k)=U12+U22+…+Uk2.
Плотность вероятности для 2(k) определяется
формулой
x 0
0,
k 2
x
f 2 x
,
1
2
2
e , x 0
2k / 2 Г k / 2 x
где Г(a) – гамма-функция Эйлера

8. Непрерывные распределения

Распределение Стьюдента
Распределением Стьюдента с k степенями свободы
называется распределение случайной величины T(k), равной
отношению двух независимых случайных величин U и
.
т.е.
где U имеет нормальное распределение N(0,1).
Распределение Стьюдента с k степенями свободы имеет
плотность вероятности fT(x):

9. Непрерывные распределения

Распределение Фишера
Распределением Фишера с k1 и k2 степенями свободы
называется распределение случайной величины F(k1,k2),
равной отношению двух независимых случайных величин
2(k1)/k1 и 2(k2)/k2, т.е
Распределение Фишера с k1 и k2 степенями свободы имеет
плотность вероятности fF(x):

10. Квантиль распределения

Квантилью
порядка
p
распределения
случайной величины X непрерывного типа
называется число tp, удовлетворяющее неравенству
P{X<tp}=p (т. е. квантиль – это значение, которое
заданная случайная величина не превышает с
фиксированной вероятностью). Если FX(x) –
функция распределения случайной величины X, то
квантиль tp находится из уравнения FX(tp)=p.

11. Дискретные распределения в MATLAB

Имена функций для расчета плотностей вероятности оканчиваются
буквами pdf (probability density function)¸ а для расчета функций
распределения – буквами cdf (cumulative distribution function).
Приведем некоторые из этих функций:
y=binopdf(k,N,p) – возвращает значение вероятности биномиального
распределения с числом испытаний N и вероятностью успеха p для
числа успехов k.
y=binocdf(k,N,p) – возвращает значение функции распределения
биномиального распределения с числом испытаний N и
вероятностью успеха p для числа успехов k.
y=poisspdf(x,a) – возвращает значение вероятности распределения
Пуассона с параметром a в точке x.
y=poisscdf(x,a) – возвращает значение функции распределения для
распределения Пуассона с параметром a в точке x.

12. Непрерывные распределения в MATLAB

y=chi2pdf(x,k) – возвращает значение плотности вероятности
распределения хи-квадрат с k степенями свободы в точке x.
y=chi2сdf(x,k) – возвращает значение функции распределения
для распределения хи-квадрат с k степенями свободы в точке x.
y=exppdf(x,a) – возвращает значение плотности вероятности
экспоненциального распределения с параметром a в точке x.
y=expсdf(x, a) – возвращает значение функции распределения
экспоненциального распределения с параметром a в точке x.
y=fpdf(x,k1,k2) – возвращает значение плотности вероятности
распределения Фишера с k1, k2 степенями свободы в точке x.
y=fсdf(x, k1,k2) – возвращает значение функции распределения
распределения Фишера с k1, k2 степенями свободы в точке x.

13. Непрерывные распределения в MATLAB

y=normpdf(x,a,sigma) – возвращает значение плотности вероятности нормального
распределения с параметрами a, sigma в точке x, a – математическое ожидание,
sigma – среднее квадратическое отклонение.
y=normсdf(x,a,sigma) – возвращает значение функции распределения
нормального распределения с параметрами a, sigma в точке x, a – математическое
ожидание, sigma – среднее квадратическое отклонение.
y=tpdf(x,k) – возвращает значение плотности вероятности распределения
Стьюдента с k степенями свободы в точке x.
y=tсdf(x,k) – возвращает значение функции распределения для распределения
Стьюдента с k степенями свободы в точке x.
y=unifpdf(x,a,b) – возвращает значение плотности вероятности равномерного в
промежутке (a,b) распределения в точке x.
y=unifсdf(x,a,b) – возвращает значение функции распределения равномерного
распределения в промежутке (a,b) распределения в точке x.

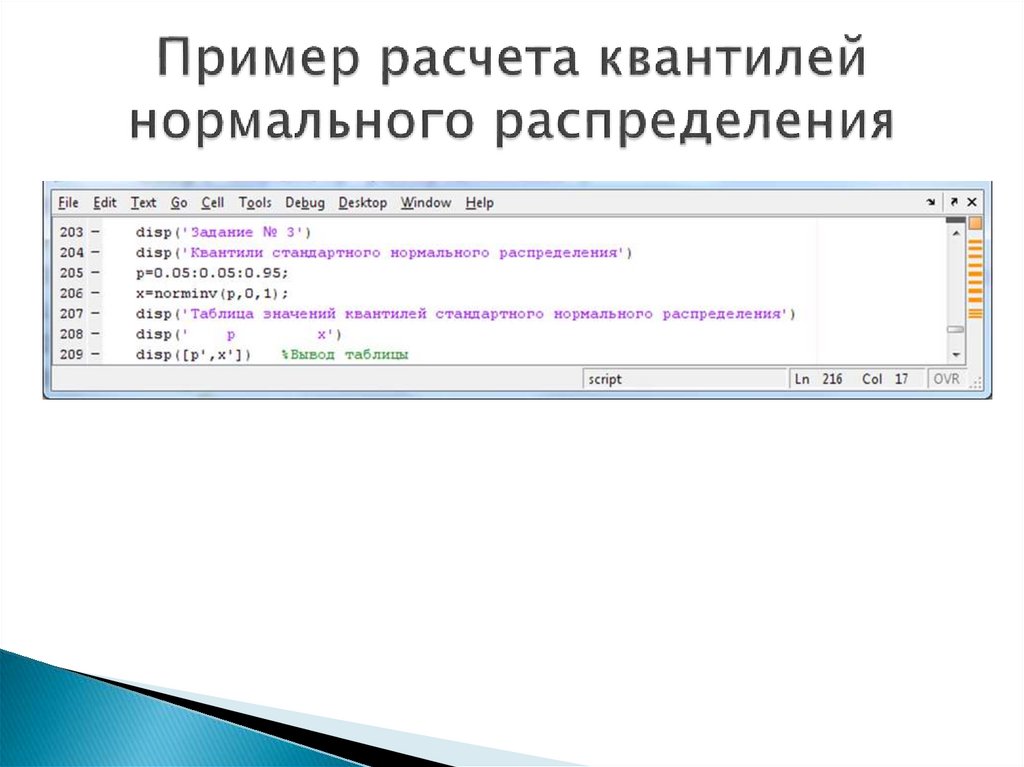
14. Квантили распределений в MATLAB

Для нахождения квантилей распределений можно использовать
следующие функции:
x=norminv(p,a,sigma) – возвращает значение аргумента функции
нормального распределения с математическим ожиданием a и
средним квадратичным отклонением sigma по значениям
вероятности p.
x=chi2inv(p,k) – возвращает значение аргумента функции
распределения хи-квадрат с k степенями свободы по значениям
вероятности p.
x=tinv(p,k) возвращает значение аргумента функции распределения
Стьюдента с k степенями свободы по значениям вероятности p.
x=finv(p,k1,k2)
возвращает
значение
аргумента
функции
распределения Фишера с k1, k2 степенями свободы по значениям
вероятности p.