Основы математической статистики в метрологии. Часть 2

1. ОСНОВЫ МАТЕМАТИЧЕСКОЙ СТАТИСТИКИ В МЕТРОЛОГИИ ЧАСТЬ 2 А.Я. Карпенко

15.06.2021
1

2. Основные законы распределения вероятностей непрерывной случайной величины

Равномерный закон распределения
0, x a
1
f ( x)
,a x b
b a
0, x b
(b - a)
D(x)
12
15.06.2021
2
a b
M(x)
2
2

3. Задание

Выведите формулы для вычисления
дисперсии и математического
ожидания равномерного закона
распределения.
Для этого используйте определение
этих характеристик.
15.06.2021
3

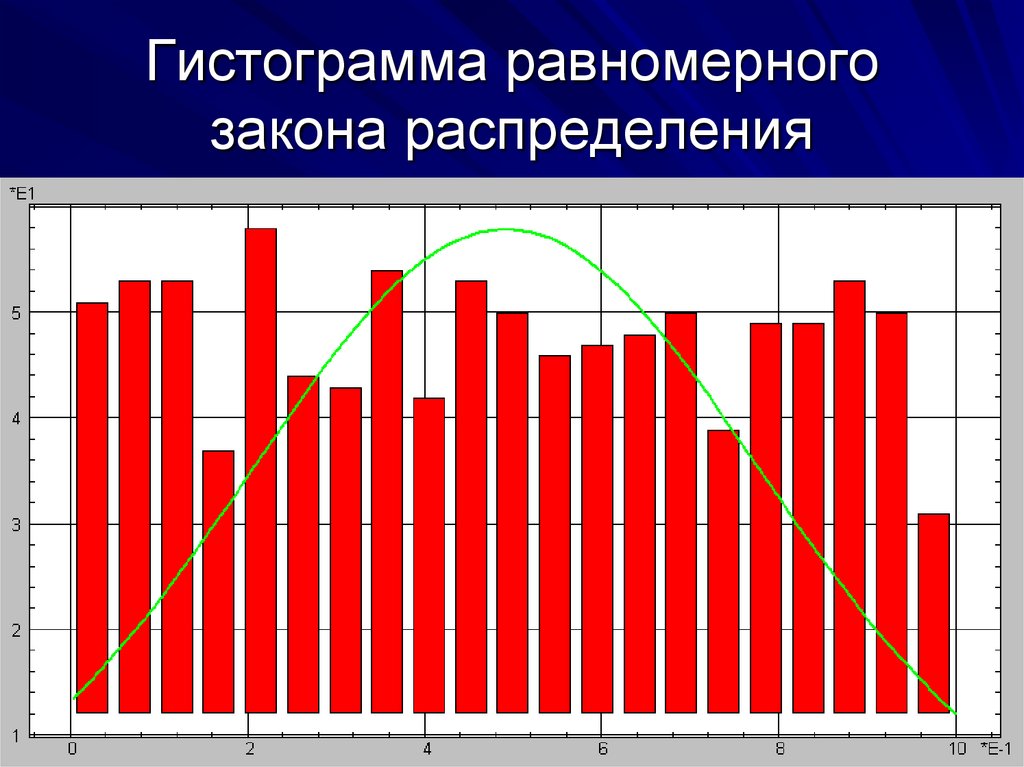
4. Гистограмма равномерного закона распределения

15.06.2021
4

5. Примеры равномерного закона распределения

Погрешности прямых измерений
Погрешность округления.
Случайная составляющая погрешности
дискретного прибора при
незначительном разбросе измерений
(1-3 дискрета)
15.06.2021
5

6. Пример из ГОСТ 8.207

Оценку суммарного СКО результата измерения вычисляют
s
2
m
i
i 1
3
~
s ( A)
2
(b - a)
4
D( )
12
12
3
2
15.06.2021
2
2
6

7. Нормальный закон распределения

(x m
f ( x)
1
x 2
e
x
)
2
x2
2
N(mx,σx)
15.06.2021
7

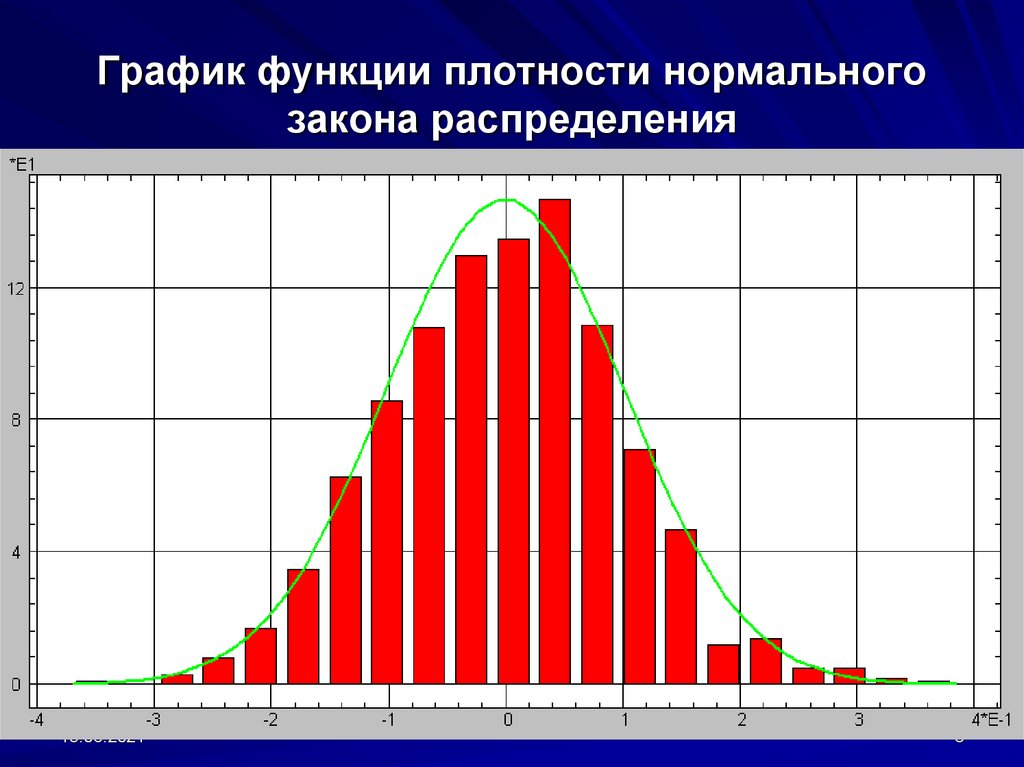
8. График функции плотности нормального закона распределения

15.06.2021
8

9. Нормированная случайная величина

x mx
U
x
Задание:
Доказать, что для нормированной
случайной величины
M(u) = 0
2(u) = 1
15.06.2021
9

10. Вопрос

Пусть три случайные величины X,Y,Z имеют
нормальное распределение с известными
математическими ожиданиями и
дисперсиями (предположим, имеются три
измерительных канала температуры):
M(X)=50, D(X)=0,3 ,
M(Y)=70, D(Y)=0,5,
M(Z)=90, D(Z)=0,7
Постройте функции плотности
распределения f(x), f(y), f(z).
Постройте для них нормированные функции
плотности распределения.
15.06.2021
10

11. Распределение 2

Распределение 2
Пусть Z1, Z2 ... Z
независимые
нормированные случайные величины N(0,
1).
M(Z)=0, D(Z)=1
U
ν
i 1
2
Zi
- есть хи-квадрат ( 2 ) распределение с
параметром . Этот параметр
называется числом степеней свободы.
15.06.2021
11

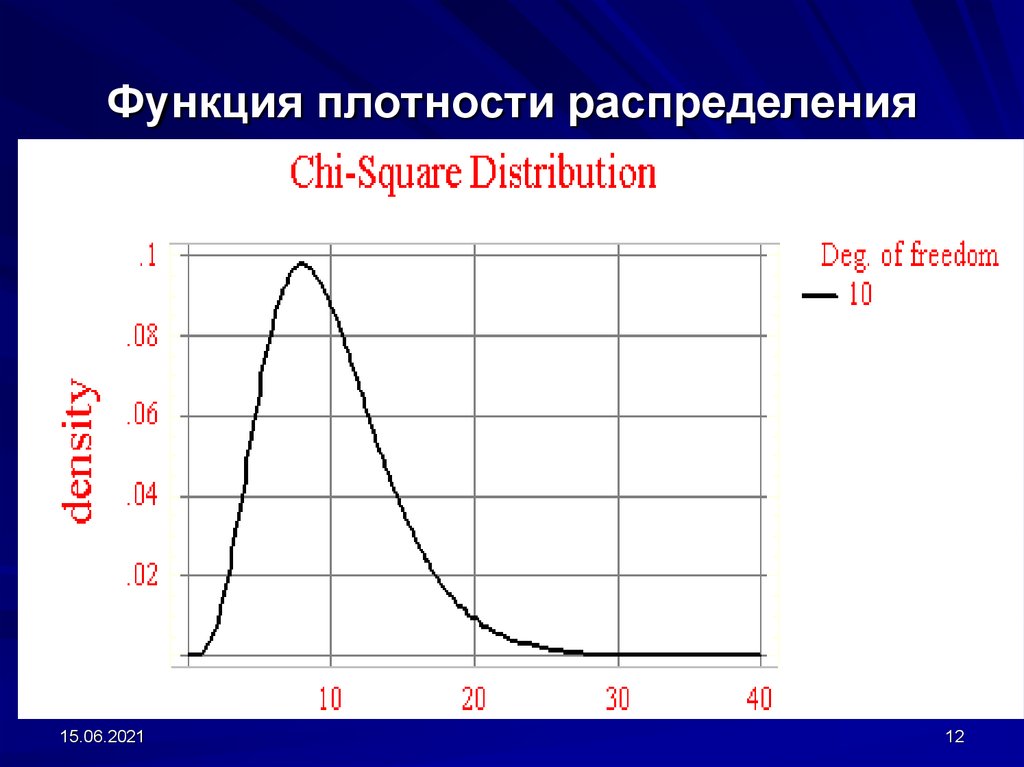
12. Функция плотности распределения

15.06.2021
12

13. Пример распределения 2

Пример распределения 2
Оценка дисперсии по выборке
S x2 ˆ x2
S x2
2
x
1 n
2
(
x
m
)
ˆx
i
n 1 i 1
1
( xi x ) 2
n 1
x2
В дальнейшем будем
использовать эту статистику
15.06.2021
(n 1) S x2
2
x
( xi x ) 2
(n 1) S
x2
2
x
2
x
13

14. Распределение Стъюдента

Z → N(0,1), V → 2( )
Z,V – независимые
Z
t
V
M(t)=0
D(t)= / -2
случайная величина t (t-статистика) ,
- распределение Стъюдента
15.06.2021
14

15. Функция плотности распределения

15.06.2021
15

16. Пример

x x
В чем отличие
x
и
x x
Sx
x x
t
x x
S
2
x
x
(n 1) S
(n 1)
2
x
2
x
Z
V
(n 1)
Вопрос :
Приведите примеры использования распределения
Стъюдента в Ваших практических задачах.
15.06.2021
16

17. Распределение Фишера

Если U, V – независимые случайные величины,
U – имеет 2( 1) с 1 степенями свободы,
V - имеет 2( 2) с 2 степенями свободы
U
F
1
V
имеет распределение Фишера
с 1 и
2 степенями свободы
2
15.06.2021
17

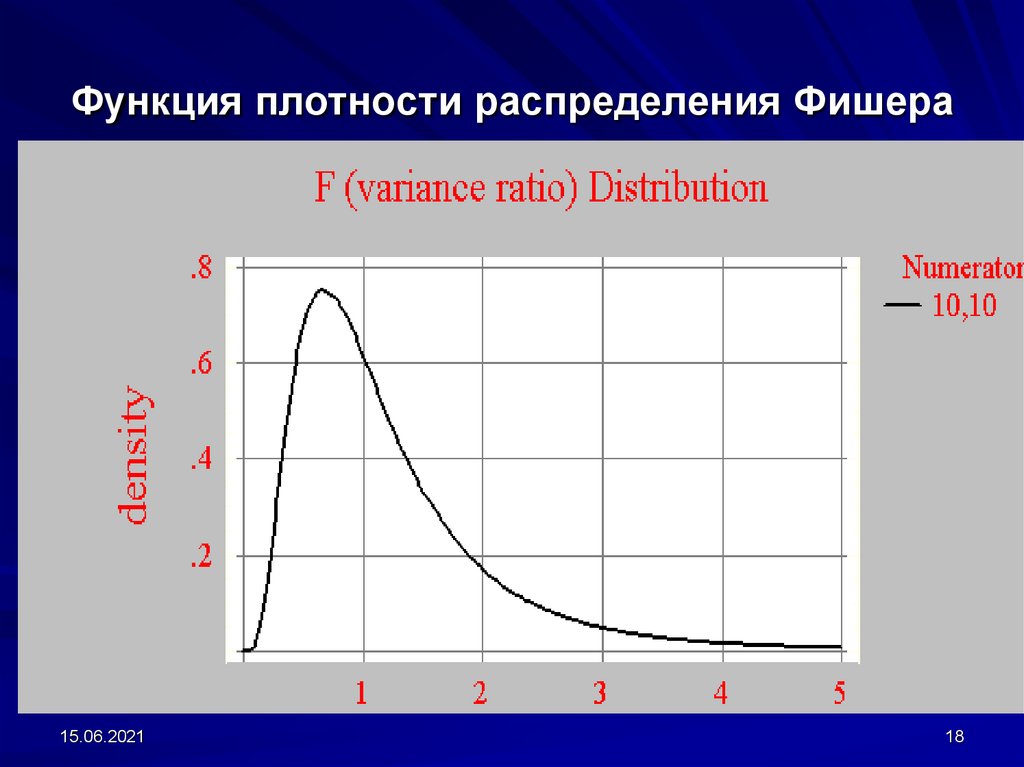
18. Функция плотности распределения Фишера

15.06.2021
18

19. Пример

Проверяется гипотеза о равенстве дисперсий двух выборок
X: x1, x2, ..., xn
Y: y1, y2, ..., ym
Отношение двух выборочных нормированных дисперсий есть
распределение Фишера с n-1 и m-1 степенями свободы.
(n 1) S x2
U
x2 x2 (n 1)
n 1
F 2
V
Sy
(m 1) S y2
y2 y2 (m 1) m 1
S x2
Вопрос: Приведите примеры использования распределения Фишера в Ваших
практических задачах.
15.06.2021
19

20. Что такое выборка?

Выборкой называют
последовательность независимых
одинаково распределенных случайных
величин.
- случайная величина
x1, x2, …, xn – выборка
15.06.2021
20

21. Показатели описательной статистики

Показатели положения (относительно среднего)
среднее арифметическое
1 n
X mˆ x xi
n i 1
среднее геометрическое
x G n x1 x 2 ... x n
медиана P(x M) = P(x M) = 1/2
мода - положение max
15.06.2021
21

22. Показатели рассеяния

Дисперсия
n
1
2
2
ˆ
S x D( x)
( xi mˆ x )
n 1 i 1
Стандартное отклонение
Размах
S x ˆ x Dˆ ( x)
xmax – xmin
Межквартальный размах – 50% выборки
15.06.2021
22

23. Показатели формы

Асимметрия
Эксцесс
Моменты
15.06.2021
M[ M ( )]3
3
/
2
[D( )]
4
M[ M( )]
[D( )]2
μ3
As 3
σ
μ4
Ek 4
σ
k M [( X M ( X )) ]
k
23

24. Квантиль

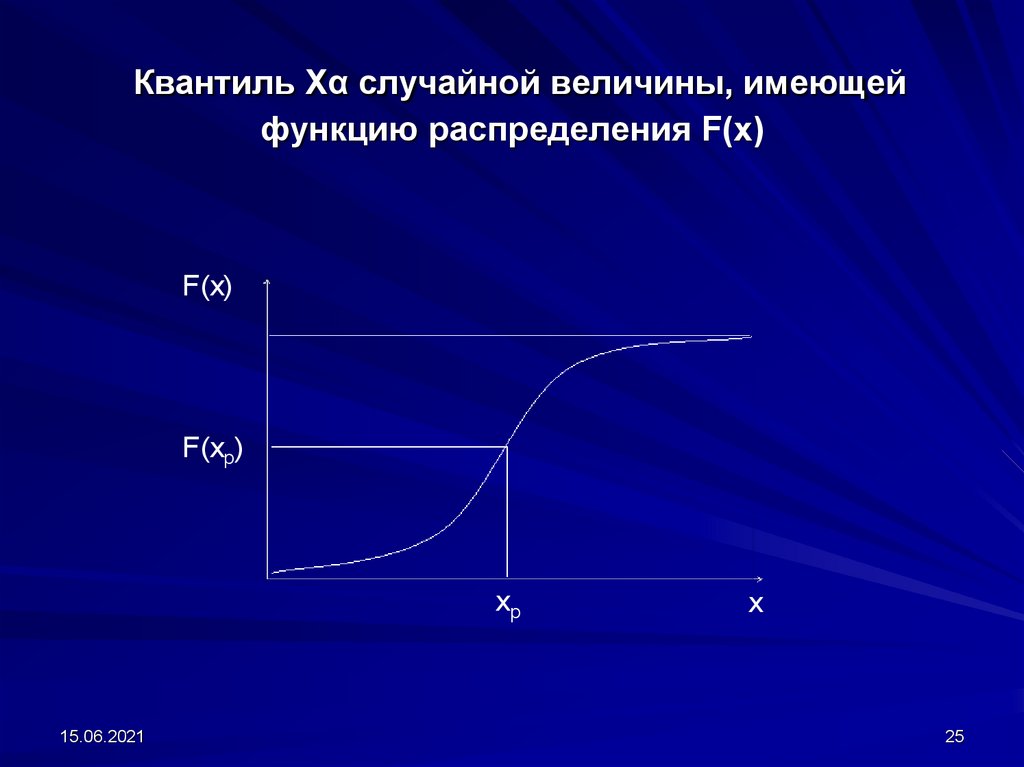
Квантилью уровня α (или α – квантилью) непрерывной
случайной величины ξ , имеющей непрерывную функцию
распределения F(x), называется значение Xα для которого
P (ξ< Xα) = α
Часто встречающиеся в практике квантили.
Медиана - квантиль, соответствующая значению α =0,5
Верхняя квартиль – квантиль, соответствующий значению
α =0,75
Нижняя квартиль – квантиль, соответствующий значению
α =0,25
Децили – квантили уровней 0,1; 0,2; ... , 0,9.
15.06.2021
24

25. Квантиль Xα случайной величины, имеющей функцию распределения F(x)

F(x)
F(xp)
xp
15.06.2021
x
25

26. Примеры решения прямой задачи в EXCEL

Для нормального закона распределения,
=НОРМСТРАСП(1.96) = 0.975002
=НОРМСТРАСП(-1.96) = 0.024998
Для распределения Стъюдента
=СТЬЮДРАСП(1.96;100;1) = 0.026389
=СТЬЮДРАСП(1.96;200;1) = 0.025692
1.96 – заданное значение X,
100,200 – число степеней свободы,
1 - односторонний интервал
15.06.2021
26

27. Примеры решения обратной задачи в EXCEL

Для нормального закона распределения по заданной
вероятности найдем квантиль
=НОРМСТОБР(0.025) = -1.96
=НОРМСТОБР(0.975) = 1.96
Решение обратной задачи для распределения Стъюдента
=СТЬЮДРАСПОБР(0.05;500) = 1.96472
Соответствует Р= 0.975
=СТЬЮДРАСПОБР(0.01;500) = 2.585698
Соответствует Р= 0.995
15.06.2021
27

28.

Спасибо
за
Внимание !!!
15.06.2021
28

29.

Предела
для СОВЕРШЕНСТВА нет
!!!
15.06.2021
29