Измерения в геометрии

1. Измерения в геометрии

2.

Часть пространства, занимаемого геометрическим телом , называется
объемом этого тела
Любая фигура на плоскости
имеет свою площадь
Любое тело в пространстве
обладает объемом
S – это положительная величина,
численное значение которой обладает
следующими свойствами:
V – это положительная величина,
численное значение которой обладает
следующими свойствами:
Равные фигуры имеют равные
площади
Равные тела имеют равные объемы
Если фигура, составлена из нескольких
фигур, то её площадь равна сумме
площадей этих фигур
Если тело разбито на части, то
объем равен сумме объемов этих
частей
В качестве единицы измерения
площади обычно берут квадрат со
стороной равной единице измерения
отрезков
Объем куба, ребро которого равно
единице длины, равен единице

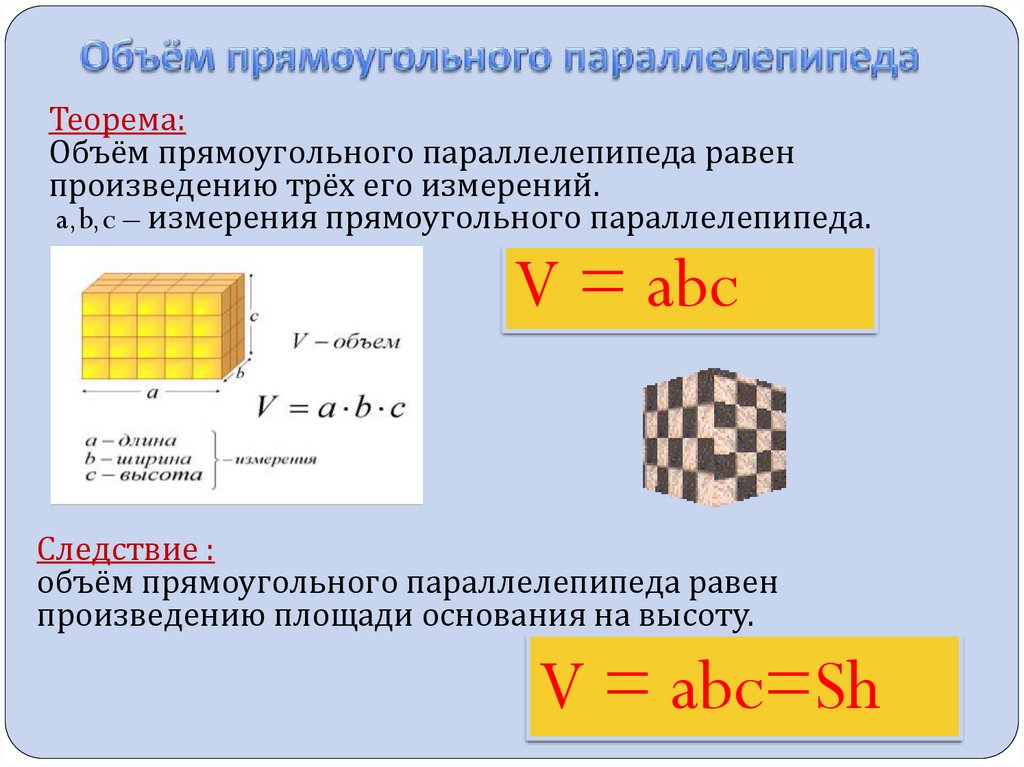
3. Объём прямоугольного параллелепипеда

Теорема:
Объём прямоугольного параллелепипеда равен
произведению трёх его измерений.
a,b,c – измерения прямоугольного параллелепипеда.
V = abc
Следствие :
объём прямоугольного параллелепипеда равен
произведению площади основания на высоту.
V = abc=Sh

4. Найдите объем тела

б)6120см3
а) 160дм3
В)186дм3

5. Задача №4

Кирпич размером 25 Х 12 Х 6,5 см
имеет массу 3,51 кг.
Найдите его плотность.
Задача №4
Дано:
Параллелепипед
длина a =AB =25 см;
ширина b=BC=12 см;
высота c=CC1=6,5 см
масса 3,51 кг
Найти: p плотность
Решение:
m
V
1. Формула плотности
2. Формула объема параллелепипеда
V abc
3. Плотность кирпича вычислим по формуле
3,51êã
(25 12 6,5)ñì
3
3510 ã
1950ñì 3
1,8
m
abc
ã
ñì 3
Îòâåò : 1,8
ã
ñì 3

6. Задача №5

Требуется установить резервуар для воды емкостью
10 м3 на прямоугольной площадке размером 2,5 Х
1,75 м, служащей для него дном. Найдите высоту
резервуара.
Задача №5
Дано:
Параллелепипед
объем V=10м3;
длина a =AB =2,5 м
ширина b=BC=1,75 м;
Найти: высоту c=CC1
Решение:
1. Формула объема параллелепипеда
V abc
2. Из формулы объема выразим высоту с=СС1
10 ì 3
ñ
(2,5 1,75) ì
2
10 ì 3
4,375 ì
2
V
c
ab
ì
2,3
ì
3
2
2,3 ì
Îòâåò : 2,3 ì

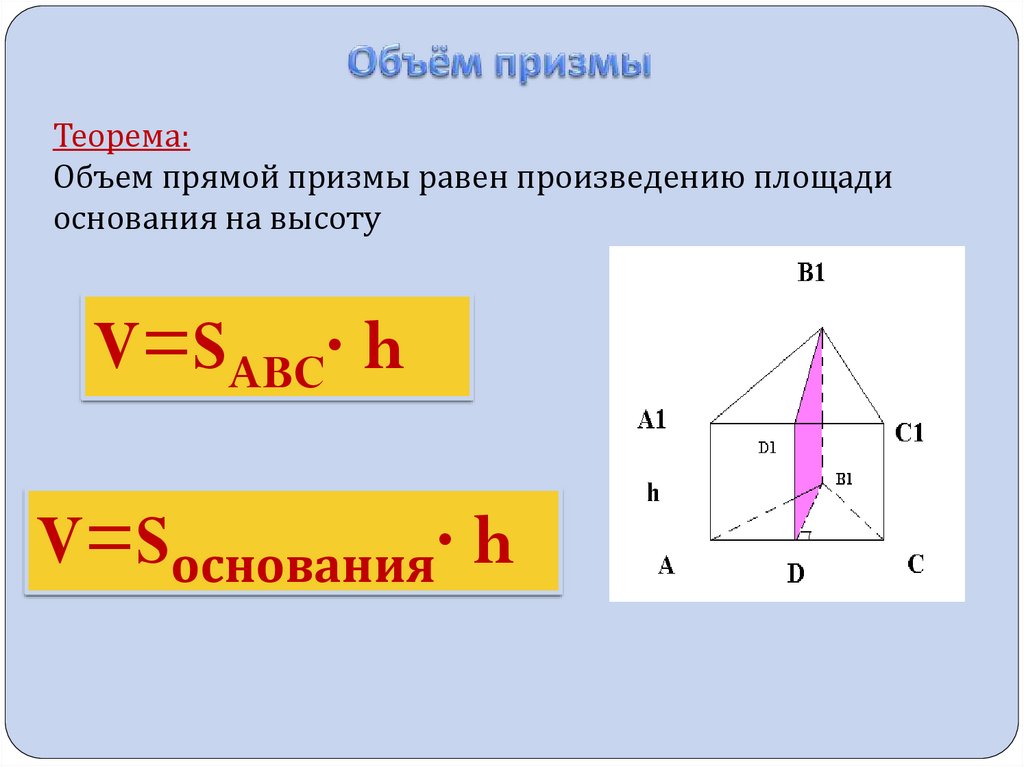
7.

Теорема:
Объем прямой призмы равен произведению площади
основания на высоту
V=SABC∙ h
V=Sоснования∙ h

8. Задача №8

Диагональ правильной четырехугольной
призмы равна 3,5 см, а диагональ боковой
грани 2,5 см. Найдите объем призмы.
Задача №8
Дано:
Четырехугольная призма
AC1= 3,5см – диагональ призмы;
DC1 =2,5см – диагональ грани
Найти: V – объем призмы
Решение:
1. Формула объема призмы
V Sосн. h
Sосн = AD*DC, h=CC1
2. Т.к. призма правильная все углы по 900,стороны основания равны
3. Рассмотрим треугольник AC1D. По т. Пифагора найдем AD
AD AC1 DC1
2
2
3,52 2,52
6 (см)
4. Рассмотрим треугольник DC1C. По т. Пифагора найдем C1C
2
2
2
2
2
СС1 DC1 DC 2 DC AD СС1 DC1 AD 2,5 ( 6 ) 6,25 6 0,25 0,5(см)
5. Найдем
S ABCD AD DC 6 6 36 6(см 2 )
6. Найдем объема призмы по формуле
V Sосн. h 6см 2 0,5см 3см 3
Ответ : 3см 3

9. Задача №9

Боковые ребра наклонной треугольной призмы
равны 15 м, а расстояния между содержащими
их параллельными прямыми 26 м, 25 м и 17 м.
Найдите объем призмы.
Задача №9
Дано:
Треугольная призма
AВ= 26м;BC=25м; AC=17м
AA1=h=15м
Найти: V – объем призмы
Решение:
1. Формула объема призмы
V Sîñí . h
2. По формуле Герона найдем площадь основания
3. Найдем периметр треугольника ABC
4. Тогда
S p( p AB)( p BC )( p AC)
68
26 25 17
34 ì
p
2
2
S 34(34 26)(34 25)(34 17) 41616
5. Найдем объем призмы по формуле
204ì
2
V Sîñí . h 204 ì 2 15 ì 3060ì
Îòâåò : 3060 ì
3
3

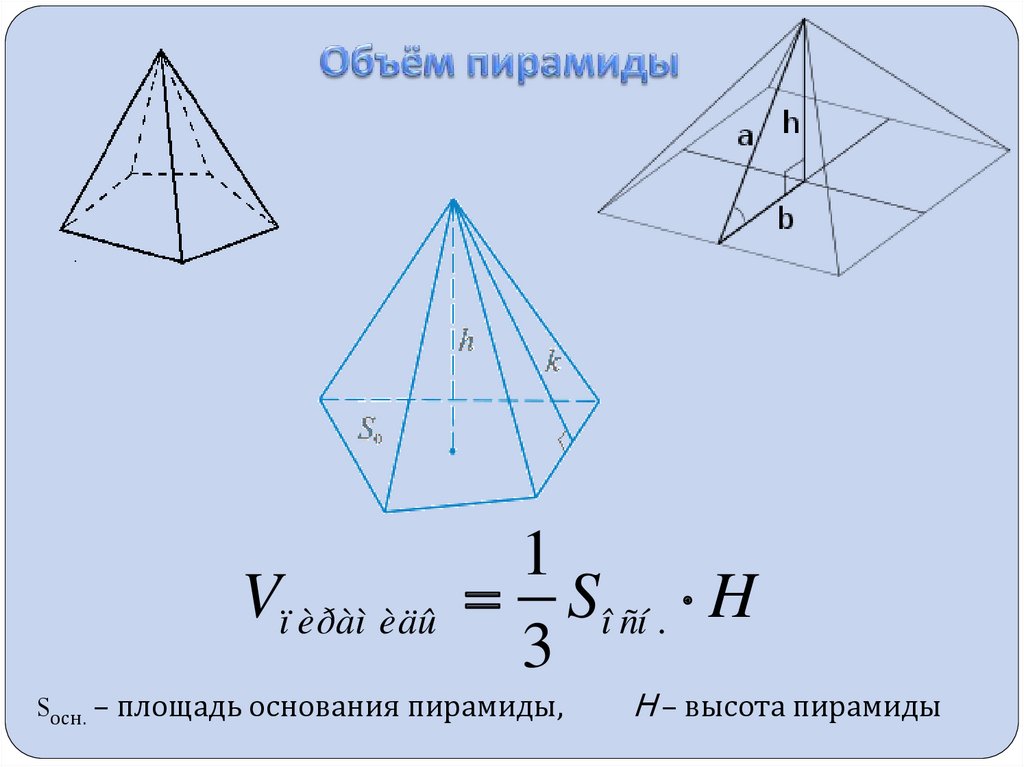
10.

Vï èðàì èäû
1
Sî ñí . H
3
Sосн. – площадь основания пирамиды,
H – высота пирамиды

11. Задача №12

Основание пирамиды - прямоугольник со
сторонами 9 м и 12 м; все боковые ребра равны
12,5 м. Найдите объем пирамиды.
Дано:
Прямоугольная пирамида
AВ= 9м;BC=12м; AS=12,5м
Найти:
V – объем пирамиды
S
В
А
С
O
D
1. Формула объема пирамиды
2. Найдем площадь основания
Решение:
1
V S осн. h высота пирамиды SO
3
Sосн AB BC 9 м 12 м 108 м 2
3. Найдем диагональ AC из треуг. ABC
4. Найдем SO из треуг. AOS
Задача №12
AC AB2 BC 2 92 122 225 15( м)
SO SA2 AO2 12,52 7,52 100 10
3
1
1
2
1080
м
3
V S осн. h 108 м 10 м
360
м
3
3
3
Ответ : 360 м 3

12. Задача №13

Основание пирамиды- равнобедренный треугольник
со сторонами 6 см, 6 см и 8 см. Все боковые ребра
равны 9 см. Найдите объем пирамиды.
S
A
O
Дано:
Треугольная пирамида
AВ= 6м;BC=6м; AC=8м; AS=9м
Найти:
V – объем пирамиды
B
Решение:
C
1
S îñí
1. Формула объема пирамиды V
3
Задача №13
.
h
2. По формуле Герона найдем площадь основания S p( p AB)( p BC )( p AC)
6 6 8 20
3. Найдем периметр треугольника ABC
10 ì
p
4. Тогда
S 10(10 6)(10 6)(10 8)
5. Найдем АО, радиус окружности R
320
324
5
1
3
)
2
SO
AS R
2
2
9
9
5
2
324
5
1
S îñí . h
3
320 324 1
1
20736 144 48(ñì 3 )
5
3
3
7. Найдем объем пирамиды по формуле V
1
3
2
320 ( ì
AB BC AC
6 6 8
36
36
9
4 S ABC
4 320
80
4 5
5
6. Найдем высоту пирамиды SO из треуг. ASO
2
2