Великая и могучая теорема Пифагора

1. Великая и могучая теорема Пифагора

МУНИЦИПАЛЬНОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ
«СРЕДНЯЯ ОБЩЕОБРАЗОВАТЕЛЬНАЯ ШКОЛА № 27 Г. ЙОШКАР - ОЛЫ»
ВЕЛИКАЯ И МОГУЧАЯ
ТЕОРЕМА ПИФАГОРА
***
АВТОР:
Руководитель:
учитель алгебры и геометрии
Воробьева Елена Александровна

2.

Актуальность теоремы Пифагора.
Теорема Пифагора в геометрии важна не меньше, чем
таблица умножения в арифметике. Решение многих
геометрических задач (как в планиметрии, так и в
стереометрии), сводится к рассмотрению
прямоугольных треугольников и применению этой
замечательной теоремы. Так же большинство задач по
нахождению сторон прямоугольных треугольников
сводится к использованию этой теоремы.Я решил, что
этот материал будет интересен учащимся 8-9 классов,
при изучении темы. Помимо исторических сведений в
проект вошли доказательства теоремы Пифагора.

3.

Цель работы:
1)Изучение истории появления и развития теоремы Пифагора.
2)Изучение исторических сведений по использованию теоремы
Пифагора.
3)Рассмотрение различных видов доказательств теоремы
Пифагора.
Задачи:
1)Собрать материал о Пифагоре Самосском.
2)Узнать интересный факт о теореме Пифагора.
3) Собрать материал по различным видам доказательств
теоремы Пифагора.
4) Проанализировать и обработать собранную информацию.
5) Сделать презентацию.
6)Оформить материал.

4.

Пифагор – древнегреческий философидеалист, математик, основатель
пифагореизма, политический,
религиозный деятель. Его родиной
был остров Самос (отсюда и прозвище
- Самосский), где он появился на свет
приблизительно в 580 г. до н. э. Его
отцом был резчик по драгоценным
камням. Согласно древним
источникам, Пифагор с рождения
отличался удивительной красотой;
когда стал взрослым, носил длинную
бороду и диадему из золота. Его
одаренность также проявилась в
раннем возрасте.
Образование у Пифагора было очень хорошим, юношу обучало много
наставников, среди которых были Ферекид Сиросский и Гермодамант.

5.

В современном мире
Пифагор считается
великим математиком и
космологом древности,
однако ранние
свидетельства до III в. до
н. э. не упоминают о таких
его заслугах. Как пишет
Ямвлих про пифагорейцев:
«У них также был
замечательный обычай
приписывать всё
Пифагору и нисколько не
присваивать себе славы
первооткрывателей,
кроме, может быть,
нескольких случаев».

6.

Античные авторы нашей эры
отдают Пифагору авторство
известной теоремы: квадрат
гипотенузы прямоугольного
треугольника равняется сумме
квадратов катетов. Такое
мнение основывается на
сведениях Аполлодораисчислителя .

7.

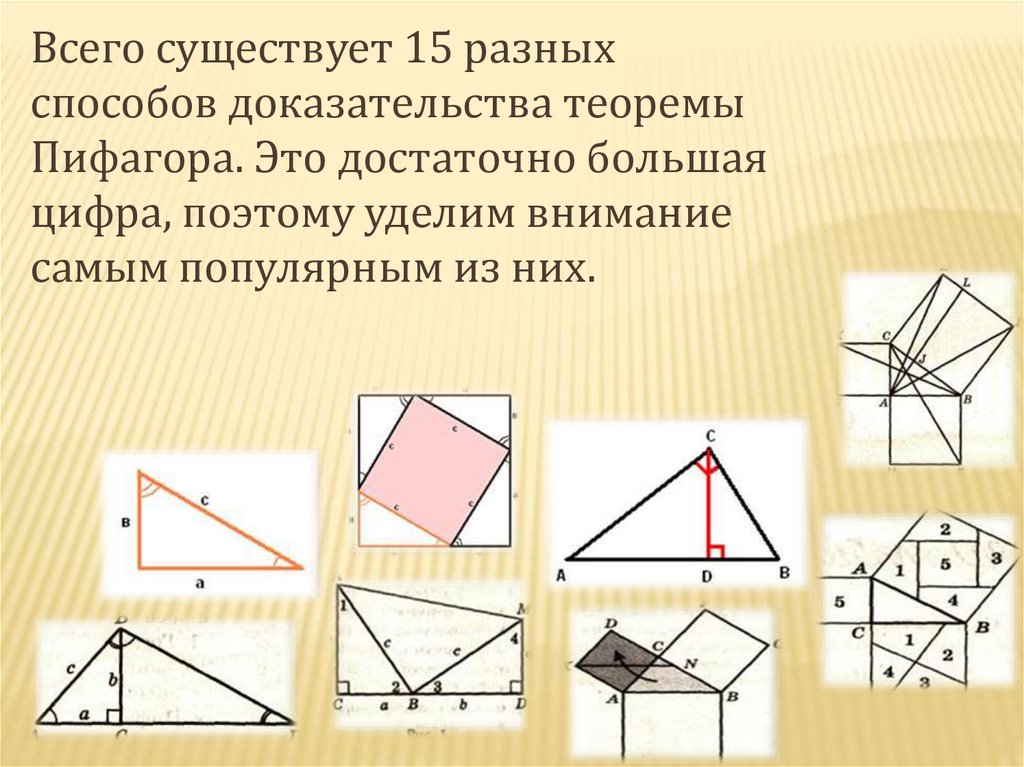
Всего существует 15 разных
способов доказательства теоремы
Пифагора. Это достаточно большая
цифра, поэтому уделим внимание
самым популярным из них.

8.

Способ 1
Рассмотрим прямоугольный
треугольник с катетами а, в и
гипотенузой с (рис.1, а).
Докажем, что с²=а²+в².
(рис.1, а)
Доказательство:
Достроим треугольник до квадрата со стороной а + в так, как показано на
рис. 1, б. Площадь S этого квадрата равна (а + в)² . С другой стороны, этот
квадрат составлен из четырех равных прямоугольных треугольников,
площадь каждого из которых равна ½ав , и квадрата со стороной с, поэтому
S= 4 * ½ав + с² =2ав + с².
Таким образом,
(а + в)² = 2ав + с²,
откуда
с²=а²+в².
Теорема доказана.
(рис.1, б)

9.

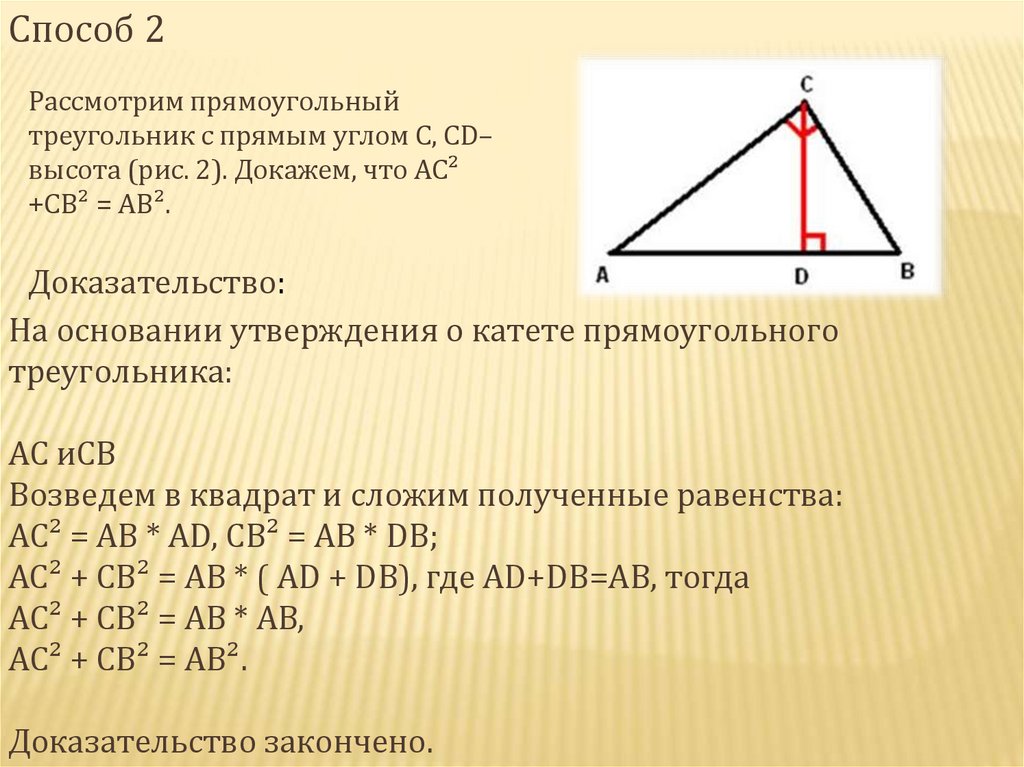
Способ 2
Рассмотрим прямоугольный
треугольник с прямым углом С, СD–
высота (рис. 2). Докажем, что АС²
+СВ² = АВ².
Доказательство:
На основании утверждения о катете прямоугольного
треугольника:
АС иСВ
Возведем в квадрат и сложим полученные равенства:
АС² = АВ * АD, СВ² = АВ * DВ;
АС² + СВ² = АВ * ( АD + DВ), где АD+DB=AB, тогда
АС² + СВ² = АВ * АВ,
АС² + СВ² = АВ².
Доказательство закончено.

10.

3 способ
Здесь: треугольник ABC с прямым углом С; отрезок BF
перпендикулярен СВ и равен ему, отрезок BE перпендикулярен
АВ и равен ему, отрезок AD перпендикулярен АС и равен ему;
точки F, С, D принадлежат одной прямой; четырехугольники
ADFB и АСВЕ равновелики, так как ABF = ЕСВ; треугольники
ADF и АСЕ равновелики; отнимем от обоих равновеликих
четырехугольников общий для них треугольник
ABC, получим:
с2 = а2 + b2.
Доказательство закончено.

11.

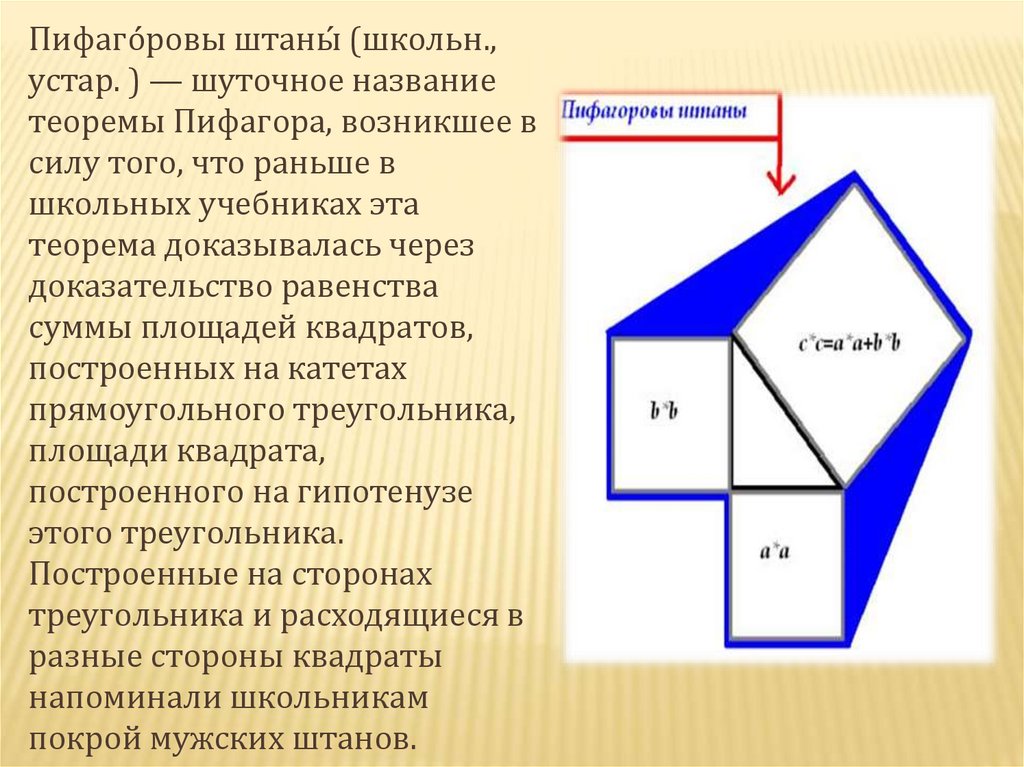
Пифаго́ ровы штаны́ (школьн.,
устар. ) — шуточное название
теоремы Пифагора, возникшее в
силу того, что раньше в
школьных учебниках эта
теорема доказывалась через
доказательство равенства
суммы площадей квадратов,
построенных на катетах
прямоугольного треугольника,
площади квадрата,
построенного на гипотенузе
этого треугольника.
Построенные на сторонах
треугольника и расходящиеся в
разные стороны квадраты
напоминали школьникам
покрой мужских штанов.

12.

Где чаще всего встречается применение теоремы Пифагора?
1)Кто в современном мире не пользуется сотовым телефоном? Каждый
абонент мобильной связи заинтересован в ее качестве. А качество в свою
очередь зависит от высоты антенны мобильного оператора. Чтобы
рассчитать, в каком радиусе можно принимать передачу, применяют
теорему Пифагора.
2)При строительстве домов и коттеджей часто встает вопрос о длине
стропил для крыши, если уже изготовлены балки. Например: в доме
задумано построить двускатную крышу (форма в сечении).
3)В лесной промышленности: для потребностей строительства
бревна распиливают на брус, при этом главная задача – получить как
можно меньше отходов. Наименьшее число отходов будет тогда, когда
брус имеет наибольший объем. Что же должно быть в сечении? Как
видно из решения сечение должно быть квадратным, а теорема
Пифагора и другие рассуждения позволяют сделать такой вывод.

13.

Заключение:
После изучения темы «Подобные треугольники» я
выяснила, что можно применить подобие
треугольников к доказательству теоремы
Пифагора. А именно, я воспользовалась
утверждением о том, что катет прямоугольного
треугольника есть среднее пропорциональное для
гипотенузы и отрезка гипотенузы, заключённого
между катетом и высотой, проведённой из
вершины прямого угла.