Similar presentations:
Свойства решений матричной игры
1.
Свойства решенийматричной игры
Чернова Екатерина Сергеевна,
доцент кафедры прикладной математики,
Кемеровский государственный университет
1
2.
Рассматриваемая матричнаяигра
Г = <U, W, H>
2
3.
ОпределениеСтратегия u1 игрока 1 доминирует
(строго доминирует) над стратегией u2,
если H (u1, w) H (u2,w) (H (u1, w) > H
(u2,w)) для любого w W.
Стратегия w1 игрока 2 доминирует
(строго доминирует) над стратегией w2,
если H (u, w1) H (u, w2) (H (u,w1) < H
(u,w2)) для любого u U.
3
4.
Доминирующие и доминируемыестратегии
Стратегии u1 и w1 называются
доминирующими (строго
доминирующими).
Стратегии u2 и w2 называются
доминируемыми (строго
доминируемыми).
4
5.
Понятие спектраСпектром смешанной стратегии игрока в
матричной игре называется множество всех
его чистых стратегий, вероятность которых
согласно этой стратегии положительна.
5
6.
Свойство 1Если чистая стратегия одного из игроков
содержится в спектре некоторой его
оптимальной стратегии, то выигрыш этого
игрока в ситуации, образованной данной
чистой стратегией и любой оптимальной
стратегией другого игрока, равен значению
матричной игры.
6
7.
Свойство 2Ни одна строго доминируемая чистая
стратегия игрока не содержится в спектре
его оптимальной стратегии.
7
8.
Понятие подыгрыИгра Г = < U , W , H > называется
подыгрой игры Г = < U, W, H >, если U U,
W W, а матрица А игры Г является
подматрицей матрицы А игры Г.
8
9.
Свойство 3Г = < U, W, H > – конечная
антагонистическая игра;
Г = < U \ х , W, H > – подыгра;
х – чистая стратегия игрока 1 в игре Г,
доминируемая некоторой стратегией u ,
спектр которой не содержит х .
9
10.
Свойство 4Г = < U, W, H > – конечная
антагонистическая игра;
Г = < U , W \ y , H > – подыгра;
y – чистая стратегия игрока 2 в игре Г,
доминируемая некоторой стратегией w ,
спектр которой не содержит y .
10
11.
Свойство 5Если для чистой стратегии х игрока 1
выполнены условия свойства 3, а для
чистой стратегии y игрока 2 – условия
свойства 4, то всякое решение игры Г = <
U \ х , W \ y , H > является решением игры Г
= < U, W, H >.
11
12.
Свойство 6Тройка (u*, w*, v) является решением игры Г
= < U, W, Н > тогда и только тогда, когда
(u*, w*, kv + а) является решением игры
Г = < U, W, kH + а >, где а – любое
вещественное число, k > 0.
12
13.
Свойство 7 (1-й игрок)u* (u ,..., u ,..., u )
- оптимальная
смешанная стратегия 1-го игрока в
матричной игре с матрицей А и ценой игры v
*
1
*
i
*
m
m
a
ij
i
u v
*
i
(1)
1
j = 1,…,n.
13
14.
Свойство 7 (2-й игрок)w* ( w ,..., w ,..., w ) - оптимальная
*
1
*
j
*
n
смешанная стратегия 2-го игрока в
матричной игре с матрицей А и ценой игры v
n
a
ij
j
w v
*
j
(2)
1
i = 1,…,m.
14
15.
Выводы из свойства 7(u, w) и v – решение матричной игры, если
выполнены (1), (2).
Обратно: найдя неотрицательные решения
(1), (2) совместно с условиями
m
u
i
1
i
1,
n
j
W
j
1,
1
получим решение МИ.
15
16.
Пример 11
2
3
4
1 2C
C
2C 3C
2 3C 3C 2 C 2C
A
3 2C 2C
C
C
4 C
C
C C 2
где С > 0.
16
17.
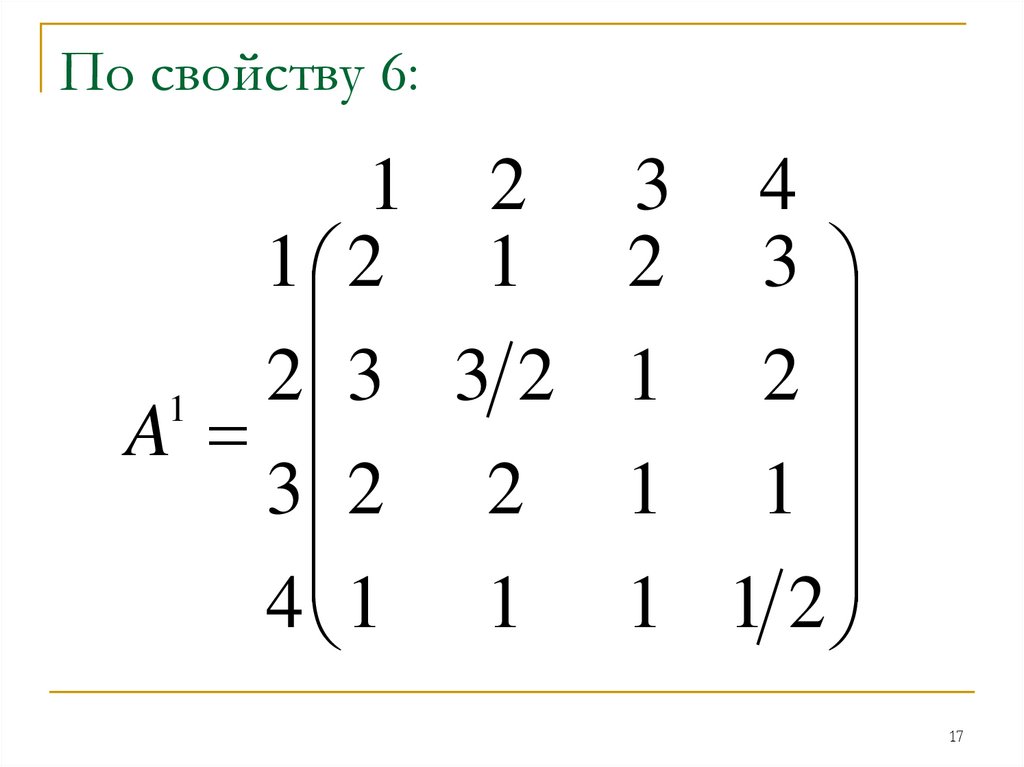
По свойству 6:1 2
1 2 1
2
3
3
2
1
A
3 2 2
4 1 1
3
2
4
3
1 2
1 1
1 1 2
17
18.
2Г
= < U \{4}, W \ {1},
2
1 1
2
A 2 3 2
3 2
1
А >
3 4
2 3
1 2
1 1
18
19.
3Г = <U \ {4,2}, W \ {1,4},
2
А>
2 3
1
1
2
3
A
3 2 1
19
20.
Если игрок 1 выбирает с равнымивероятностями стратегии 1 и 3,
ожидаемый выигрыш:
1
1
3
1 2
2
2
2
1
1
3
2 1
2
2
2
20
21.
Если игрок 2 выбирает с равнымивероятностями стратегии 2 и 3,
ожидаемый выигрыш также равен 3/2.
21
22.
Решение игры1 1
u ,0, ,0
2 2
1 1
w 0, , ,0
2 2
3C
v
2
22
23.
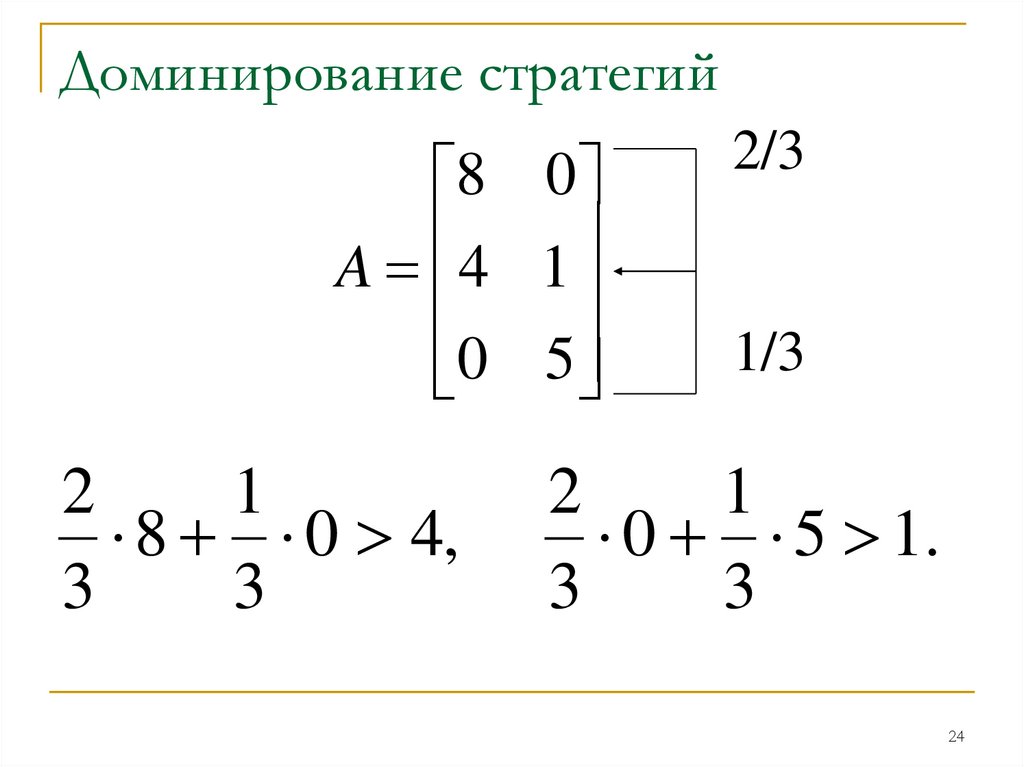
Пример 2Принцип доминирования можно обобщить
на тот случай, когда одна из стратегий
доминируется некоторой выпуклой
линейной комбинацией других стратегий.
8 0
A 4 1
0 5
23
24.
Доминирование стратегий8 0
A 4 1
0 5
2
1
8 0 4,
3
3
2/3
1/3
2
1
0 5 1.
3
3
24
25.
Подыгра исходной игры8 0
A
0
5
25

















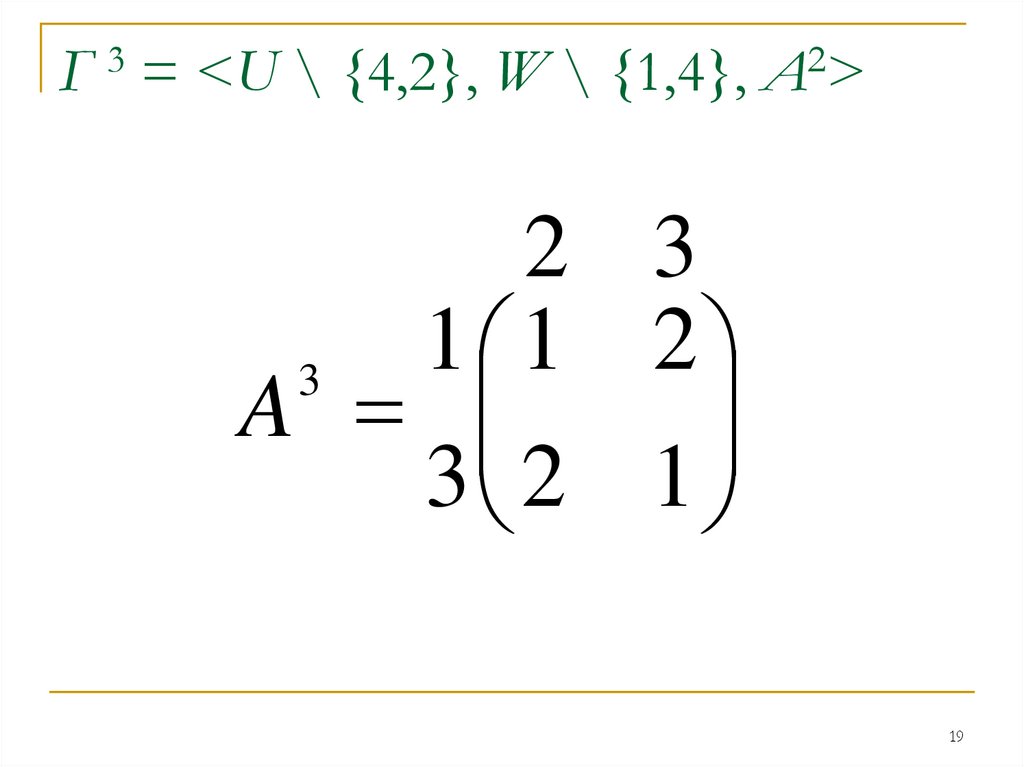





 mathematics
mathematics








