Similar presentations:
Графоаналитический метод решения 2хn игр и mx2 игр
1.
Графоаналитический методрешения 2хn игр и mx2 игр
Чернова Екатерина Сергеевна,
доцент кафедры прикладной математики,
Кемеровский государственный университет
1
2.
Игра 2xnа11 а12 ...а1n
А
а
а
...
a
21 22 2 n
2
3.
Ожидаемый выигрыш 1го игрокапри выборе 2м игроком j-й чистой стратегии:
a1 j u1 a2 j u2 , u (u1 , u2 )
4.
Задача игрока 1состоит в максимизации функции:
g (u ) min (a1 j u1 a2 j u2 )
j 1,..., n
4
5.
Выразим u1 через u2u1 1 u2 ,
g (u2 ) min ((a2 j a1 j )u2 a1 j ),
j 1,..., n
u2 [0,1]
5
6.
Цена игрыmax(g(u2)) дает значение (цену) игры v.
7.
Выводv – минимум n линейных функций одной
переменной u2.
Можно начертить графики этих функций и
затем максимизировать их минимум g(u2)
графическим методом.
7
8.
ПримерB1
С1 2
1
С2 7
2
B2
3
5
B3
11
2
8
9.
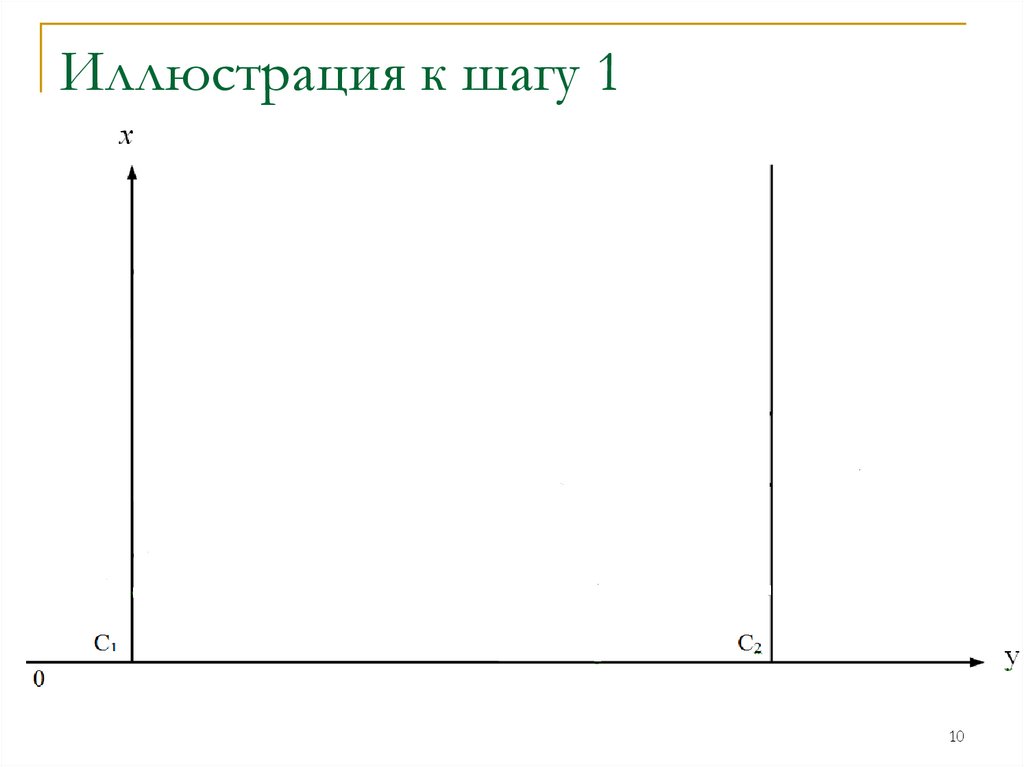
Шаг 1На плоскости хОy введём систему координат
и на оси Ох отложим отрезок единичной
длины С1С2, каждой точке которого поставим
в соответствие некоторую смешанную
стратегию игрока 1 (u, 1 – u).
В точках С1 и С2 восстановим
перпендикуляр.
9
10.
Иллюстрация к шагу 110
11.
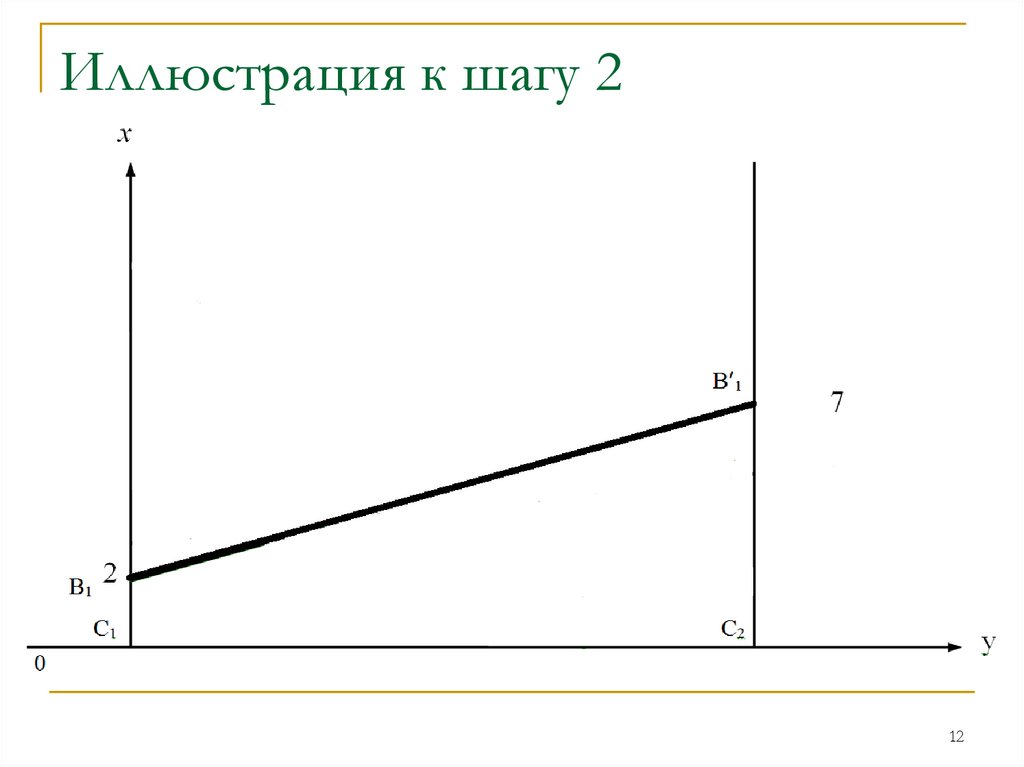
Шаг 2На первом перпендикуляре (он совпадает с
осью Оy) отложим выигрыш игрока 1 при
стратегии С1, а на втором – при стратегии
С2. Соединим между собой полученные
точки.
11
12.
Иллюстрация к шагу 212
13.
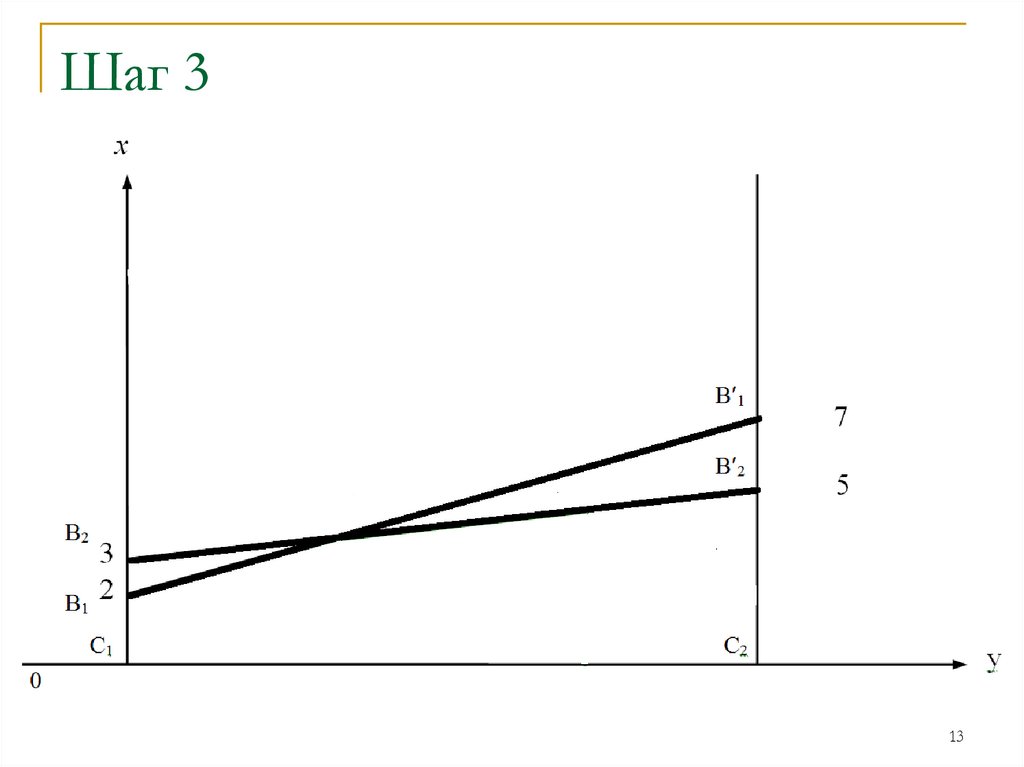
Шаг 313
14.
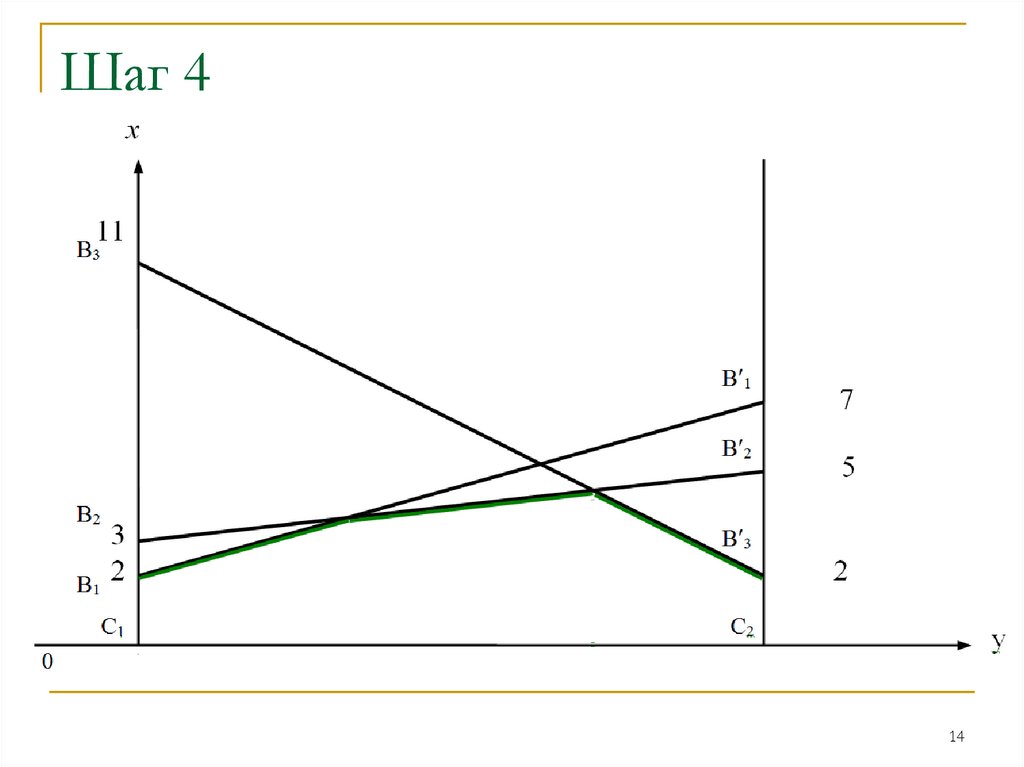
Шаг 414
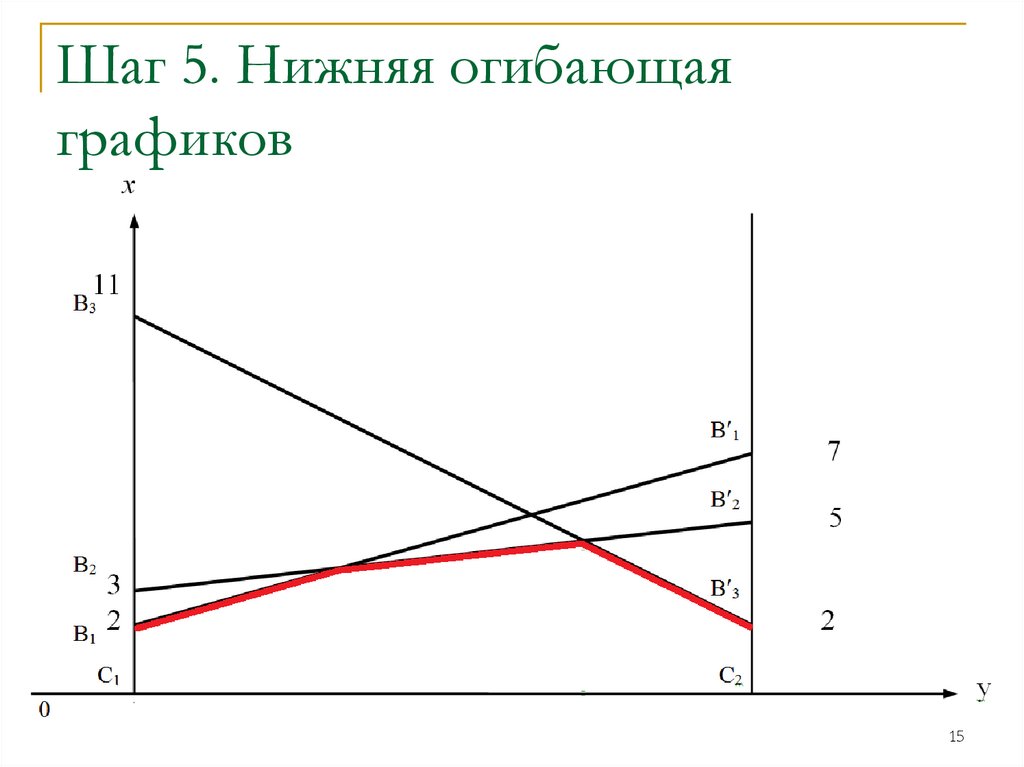
15.
Шаг 5. Нижняя огибающаяграфиков
15
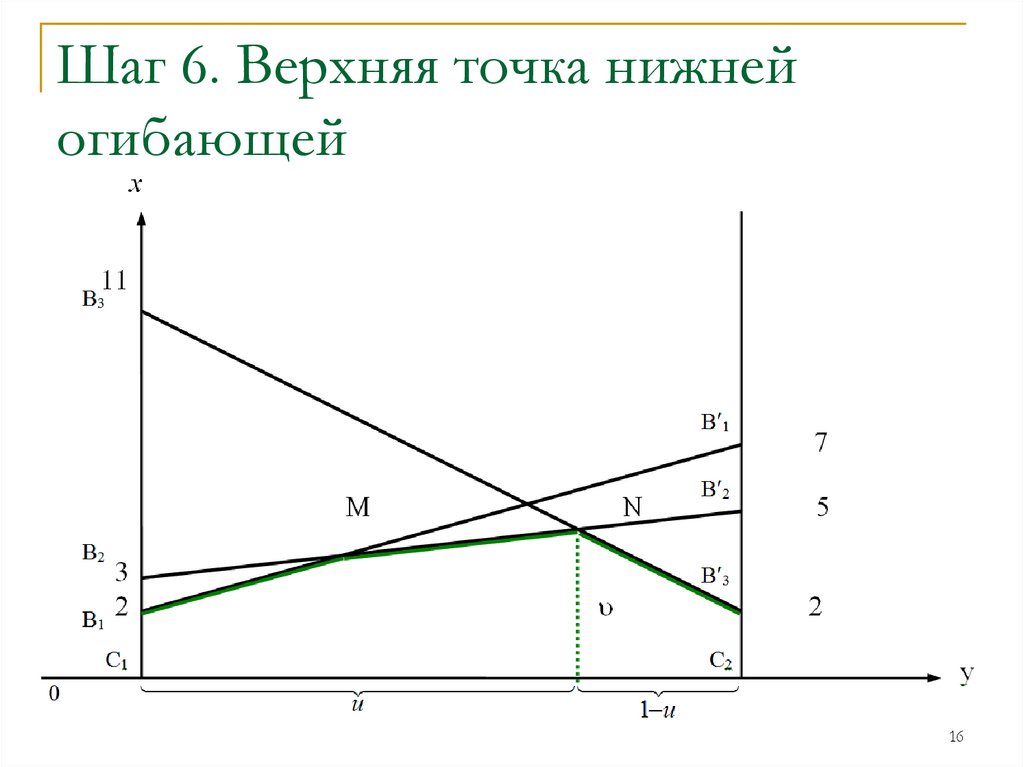
16.
Шаг 6. Верхняя точка нижнейогибающей
16
17.
Шаг 7. Построение подыгры17
18.
Шаг 8. Вычисление оптимальныхсмешанных стратегий в подыгре
u = (3/11, 8/11);
w = (9/11, 2/11);
v = 49/11.
18
19.
Шаг 9. Определение оптимальныхстратегий в исходной игре
u* = (3/11, 8/11);
w* = (0, 9/11, 2/11);
v = 49/11.
19













 mathematics
mathematics








