Similar presentations:
Теория принятия решений. Решение игр MxN
1. ТЕОРИЯ ПРИНЯТИЯ РЕШЕНИЙ
Преподаватель:доцент кафедры ИСУ, к.т.н.
Бушуева Марина Евгеньевна
2. РЕШЕНИЕ АНТАГОНИСТИЧЕСКИХ ИГР m×n
Все элементы матрицы должныбыть больше 0. Если это не так, то ко
всем элементам можно прибавить
такое число L
>0
L r max aij ,
ij
r>1
a11
a 21
A
...
a m1
a12
a 22
...
a m2
При этом цена игры возрастает на L
... a1n
... a 2 n
... ...
... a mn
3.
0P1 применит свою оптимальную стратегию X 0 ( x10 ,..., xm
)
Тогда его выигрыш будет не менее V при любых действиях игрока P2 .
В частности, если игрок P2 . применит свою чистую стратегию Вj, то
выигрыш P1 составит:
Пусть игрок
a x a x ... a x V
0
1j 1
0
2j 2
0
mj m
Поделим это неравенство на V и обозначим
a1 j z1 a 2 j z 2 ... a mj z m 1
j = (1, …, n)
0
i
x
zi
V
(i = 1, …, m)
j = (1, …, n), zi ≥ 0
4.
mдолжно выполняться условие
0
xi
1
i 1
Поделим это выражение на V и в новых обозначениях запишем
1
z1 z2 ... z m
V
Поскольку игрок
P1 стремиться к максимуму V, то целевая функция
будет иметь вид:
m
f ( z1 ,..., z m ) z i min
i 1
5.
Задача (1) – задача линейного программированияРешение задачи (1).
(1)
m
zi min
i 1
m
aij zi 1 ( j 1,n)
i 1
zi 0
Тогда
V
z
0
1
0
xi
m
z
i 1
0
i
0
0
( z1 ,..., zm )
0
zi
m
i 1
0
zi
(i = 1, …, m).
6.
Аналогичные рассуждения можно проделать для игрока P2:Пусть он применяет оптимальную смешанную стратегию Y
а игрок P1– чистую стратегию Аi
0
0
0
( y1 ,..., yn )
(i = 1, …, m).
Тогда проигрыш игрока P2 составит величину не более V:
a y ai 2 y ... ain y V
0
i1 1
0
2
Разделим это неравенство на V
получим
(i = 1, …, m)
0
n
>0
y
0
j
V
a i1 w1 ... a in wn 1
wj
(j = 1, …, n)
(i = 1, …, m),
wj 0
7.
nдолжно выполняться условие
0
yj
1
j 1
Поделим это выражение на V и в новых обозначениях получим:
n
1
wj
V
j 1
Поскольку игрок
V min
P2
стремиться минимизировать проигрыш
n
f ( w1 ,...wn ) w j max
j 1
8.
имеем задачу линейного программирования (2)(2)
n
w j max
j 1
n
a ij w j 1 (j 1, n )
j 1
w 0
j
Тогда
y
0
j
решение задачи (2).
w
0
w
0
j
(j 1,...,n)
n
w
j 1
0
0
( w1 ,..., wn )
0
j
9. ПРИМЕР 14
ЗАДАЧА КОМПЛЕКТАЦИИ ВЫЧИСЛИТЕЛЬНОГО ЦЕНТРАПредполагается организовать ВЦ коллективного пользования, который может
быть оснащен ЭВМ - 4х типов, на обработку будут приниматься данные,
относящиеся к одному из 5 видов задач (календарное планирование,
распределение
ресурсов…)Процесс решения каждой задачи требует
определенного времени, зависящего от типа ЭВМ. Расходы связанные с
деятельностью ВЦ оплачивают заказчики в следующих размерах:
виды задач
1
2
3
4
5
Э
В
М
1
2
3
4
200
300
400
700
400
400
500
300
600
600
600
500
400
500
500
200
700
800
800
100
Определить, какими ЭВМ надо оснащать ВЦ, что бы обеспечить mах прибыль
и какие задачи надо решать, что бы иметь min убытки.
10. Решение
Игрок P1 (организаторы ВЦ) имеет 4 стратегии комплектования ВЦ,Игрок
P2
(пользователи ВЦ) имеет 5 стратегий выбора задач.
В1 В4 В5
А 3 400 500 800
А4 700 200 100
B1
B4
400р+700(1-р)=Z
B5
800p+100(1-p)=Z
400р+700(1-р)= 500р+200(1-р)
5
p
6
*
500р+200(1-р)=Z
5 1
X (0,0, , )
6 6
0
V 450
11.
Пусть игрок Р2 применяет стратегию (q,1-q)Z=400q+500(1-q)
Z=700q+200(1-q)
1
q
2
*
В1 В4
А 3 400 500
А4 700 200
1
1
Y ( ,0,0, ,0)
2
2
0
Таким образом результат означает, что на ВЦ целесообразно
устанавливать машины 3 и 4 типов в соотношении 5:1. Заказчикам
наиболее выгодны задачи 1 и 4 типов в равной степени и тогда доход
будет не менее 450 усл.ед.
12. Запишем данную задачу как задачу линейного программирования
z3 z 4 min400 z3 700 z 4 1
500 z3 200 z 4 1
800 z3 100 z 4 1
zi 0
1
z3
540
1
z4
2700
13.
x0
3
z3
4
z
i 3
V
450 1
x
2700 6
450 5
540 6
0
4
i
1
m
z
i 1
i
1
1
1
2700 540
450
14.
Найдем стратегию игрока P2, решая двойственную задачу:w1 w4 w5 max
400 w1 500 w4 800 w5 1
700 w1 200 w4 100 w5 1
wi 0
1 ~ w1
2 ~ w2
3 ~ w3
z3 ~ 1
z4 ~ 2
(т.к. в пересечении прямых (1) и (2)
0
В прямой задаче 1
2
находится решение)
3 0, значит w1 , w4 - базисные переменные, w5- свободная
Уравнений 2, базисных переменных 2
Значит
1 , 2
- свободные
w5 0, 1 0, 2 0
15.
400w1 500w4 1700w1 200w4 1
w1
1
y1
w1 w4 2
0
1
1
w1
; w4
900
900
y4
0
1
2
1
1
Y ( ,0,0, ,0)
2
2
0
16. ЗАДАЧА. ВОЙНА АРМИЙ.
Две воюющие армии ведут борьбу за два пункта. Первая армиясостоит из 3-х полков, вторая из 2-х. Армия, которая посылает
больше полков в тот или иной город, занимает его и уничтожает все
направленные в этот пункт силы противника, получая 1 очко за
занятый пункт и по 1 очку за каждый уничтоженный полк противника.
Найти оптимальную стратегию для обеих армий.
Р2
(2, 0) (0, 2) (1, 1)
(3, 0)
Р1
(0, 3)
(2, 1)
(1, 2)
3
0
1
-1
0
3
-1
1
1
1
2
2
Р2
(2, 0) (0, 2) (1, 1)
(3, 0)
Р1
(0, 3)
(2, 1)
(1, 2)
5
2
3
1
2
5
1
3
3
3
4
4
17. ДЛЯ ПЕРВОЙ АРМИИ
z1 z 2 z3 z 4 min5 z1 2 z 2 3 z3 z 4 1
2
z
5
z
1
z
3
z
1
1
2
3
4
3 z3 3 z 4 4 z3 4 z 4 1
zi 0
18. ДЛЯ ВТОРОЙ АРМИИ
w1 w2 w3 max5w1 2 w2 3w3 1
2 w1 5w2 3w3 1
3w1 w2 4 w3 1
w1 3w2 4 w3 1
wi 0
1 ~ w1
2 ~ w4
3 ~ w5
z1 ~ 1
z2 ~ 2
z3 ~ 3
z4 ~ 4
19.
bw1
η3
w3
w2
L
η1
η4
η2
y
0
j
1/16
0
w
0
j
n
w
j 1
0
j
3/16
1/16
-5/16 -7/48 -1/16 -5/48
1 1 3
0
Y ( , , )
5 5 5
V
1
16 / 5
n
w
j 1
j
V 16 / 5 2 6 / 5
20. ДЛЯ ПЕРВОЙ АРМИИ
bz1
z4
z2
7/48
L
5/6
ζ1 z3
ζ3
ζ2
1/16
0
xi
0
zi
m
i 1
5/48
-1/6
X
0
0
-3/16 -1/16
7 1
1
(
, ,0, )
15 3
5
0
zi












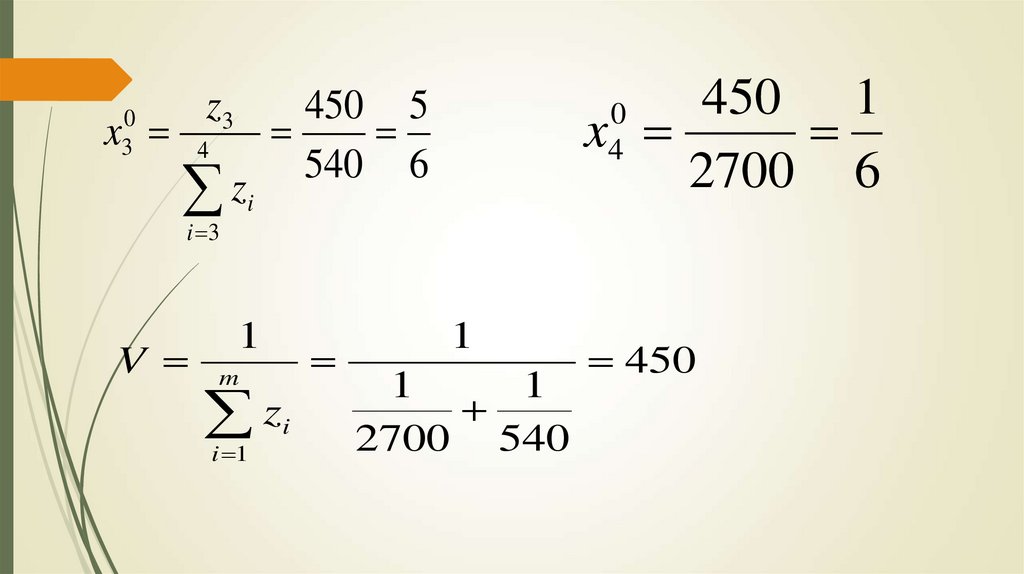







 mathematics
mathematics








