Similar presentations:
Неравенство треугольника
1.
Неравенство треугольника2.
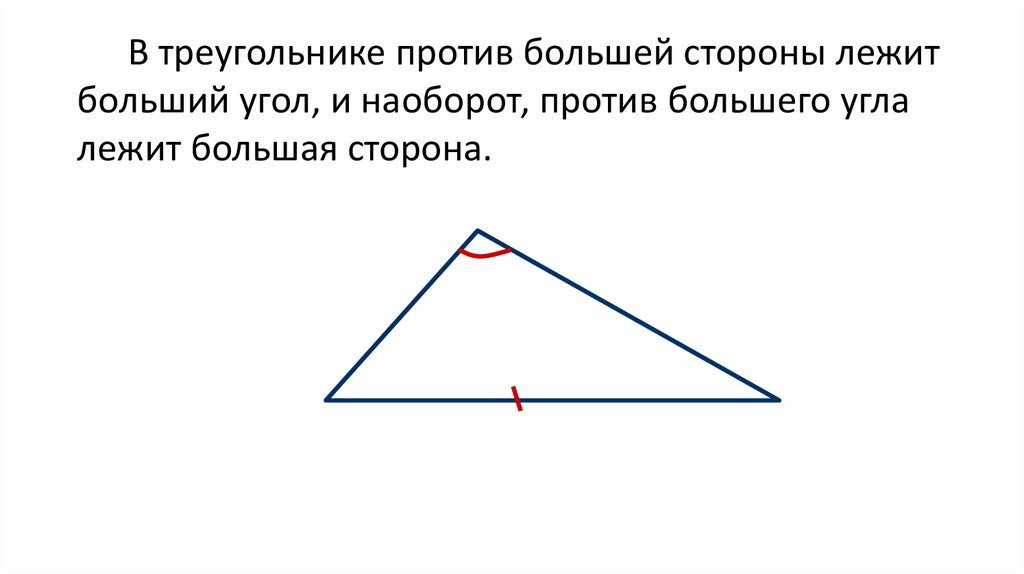
В треугольнике против большей стороны лежитбольший угол, и наоборот, против большего угла
лежит большая сторона.
3.
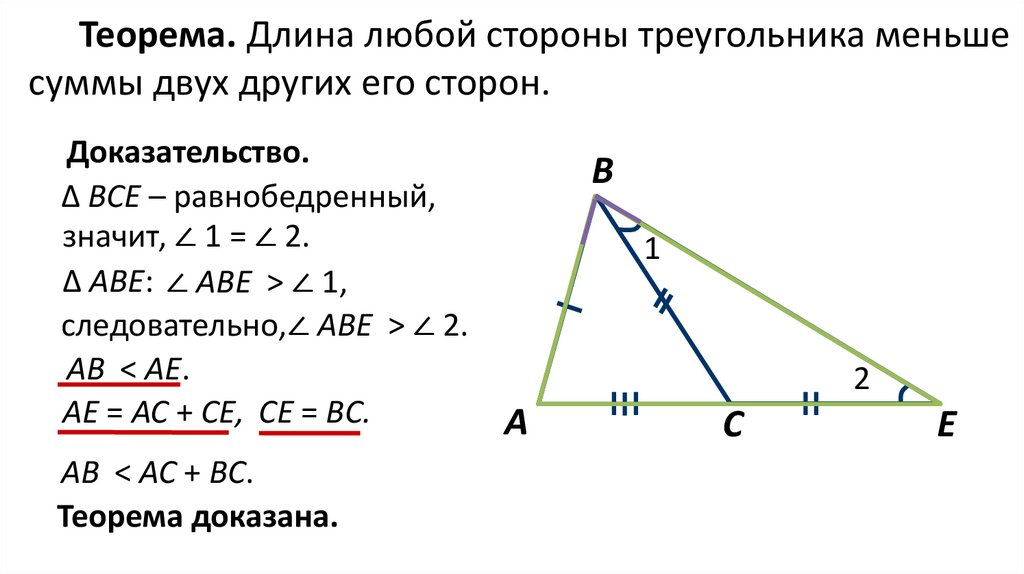
Теорема. Длина любой стороны треугольника меньшесуммы двух других его сторон.
Доказательство.
∆ ВСЕ – равнобедренный,
значит, ∠ 1 = ∠ 2.
∆ АВЕ: ∠ АВЕ > ∠ 1,
следовательно,∠ АВЕ > ∠ 2.
АВ < AE.
AE = AC + CE, CE = BC.
АВ < AC + BС.
Теорема доказана.
В
1
2
А
С
Е
4.
Следствие 1. Для любых трёх точек А, В и С, нележащих на одной прямой, справедливы следующие
неравенства:
АВ < AC + BC,
AC < AB + BC,
BC < AB + AC.
Следствие 2. Длина каждой стороны треугольника
больше разности длин двух других его сторон.
5.
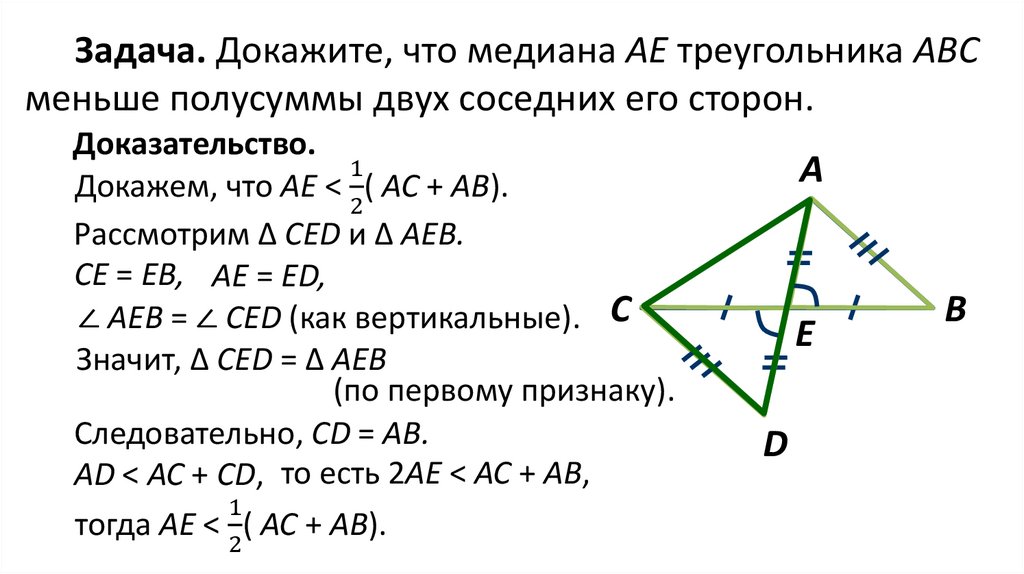
Задача. Докажите, что медиана АЕ треугольника АВСменьше полусуммы двух соседних его сторон.
Доказательство.
1
Докажем, что АЕ < ( АС + АВ).
2
Рассмотрим ∆ СЕD и ∆ АЕВ.
CE = ЕB, АE = ЕD,
∠ AEВ = ∠ CED (как вертикальные). С
Значит, ∆ СЕD = ∆ АЕВ
(по первому признаку).
Следовательно, СD = АВ.
АD < АС + CD, то есть 2АE < АС + AB,
тогда АЕ <
1
(
2
АС + АВ).
А
Е
D
В
6.
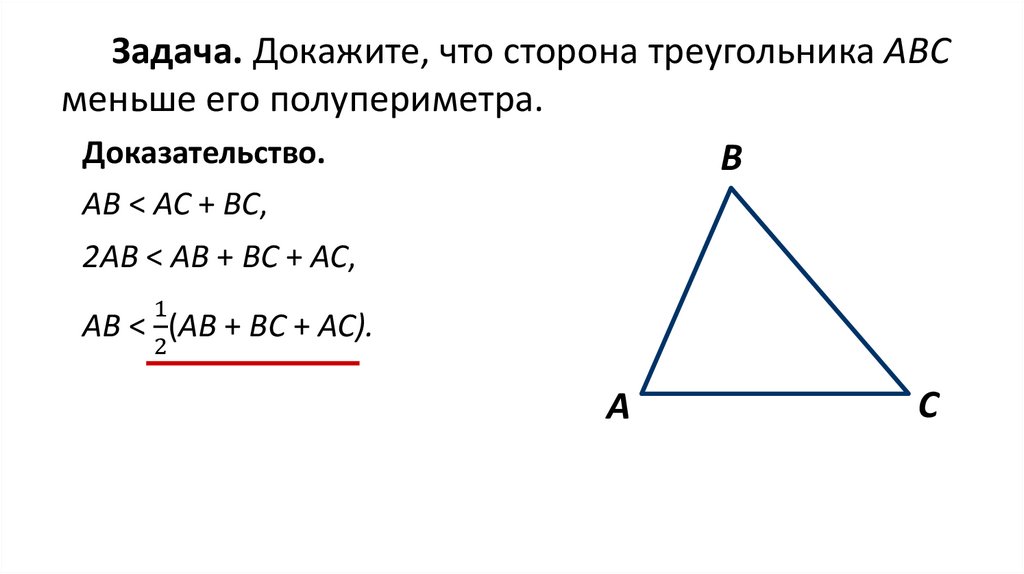
Задача. Докажите, что сторона треугольника АВСменьше его полупериметра.
Доказательство.
В
АВ < АС + ВC,
2АВ < АВ + ВC + АС,
АВ <
1
(АВ +
2
ВC + АС).
А
С


 mathematics
mathematics








