Similar presentations:
Физика колебаний и волн. Квантовая физика. Лекция № 4
1. Физика колебаний и волн. Квантовая физика.
2. Лекция № 4
Интерференция волн.1. Условия интерференции волн.
2. Классические интерференционные опыты.
3. Интерференция сферических
волн.
3. Интерференция волн (от лат. inter – взаимно, между собой и ferio – ударяю, поражаю) – пространственное перераспределение
энергии волн при наложениидвух или нескольких волн.
Интерференция волн – одно из основных
свойств волн любой природы (упругих,
электромагнитных, в т.ч. световых и др.).
Такие характерные волновые явления, как
излучение, распространение и дифракция,
тоже связаны с интерференцией.
4.
Круговая волна наповерхности жидкости,
возбуждаемая точечным
источником (гармонически
колеблющимся шариком).
Интерференция
поверхностных волн от двух
точечных синфазных
источников.
В точках, для которых r2 - r1
= λ (m + ½), поверхность
жидкости не колеблется
(узловые точки (линии))
5.
Расстояние от источника до стенки r кратно целому числуполуволн, исходная круговая волна интерферирует с волной,
отражённой от стенки, поэтому справа от источника на
оси соединяющей фиктивный и реальный источник разность
хода будет кратна целому числу волн, и круговая волна
накладывается в фазе с волной, отражённой от стенки,
увеличивая высоту гребней в интерференционной картине
6.
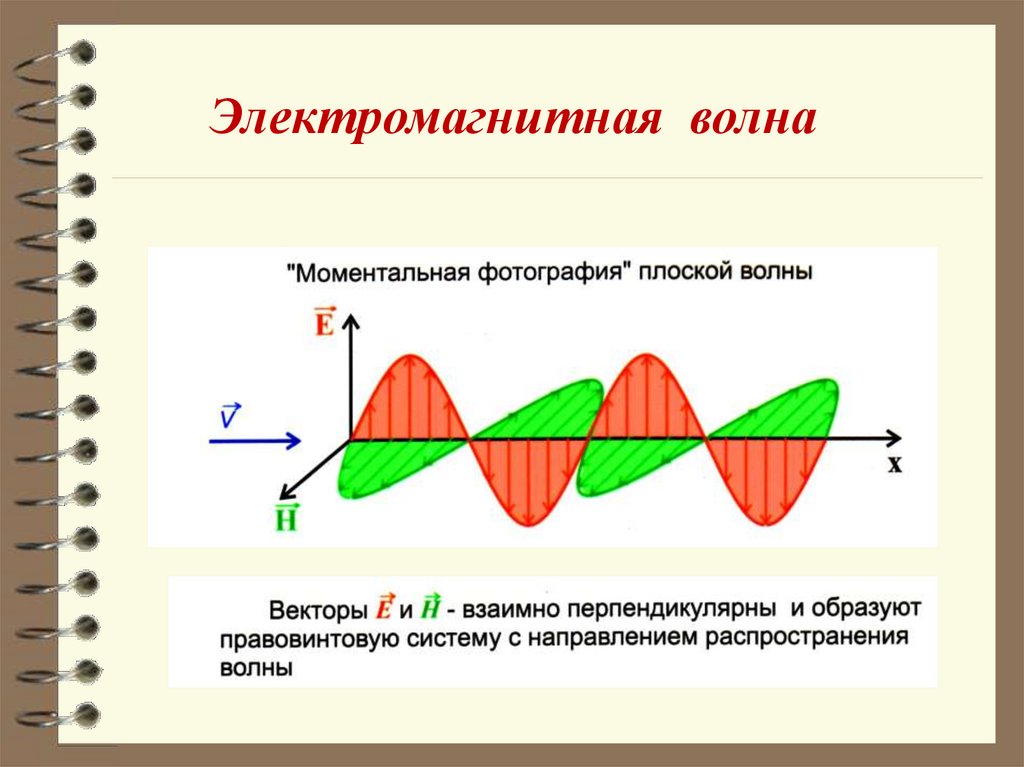
Электромагнитная волна7.
В электромагнитной волне происходят колебанияполей, а не вещества, как в случае волн на воде или в
натянутом шнуре. Электромагнитные волны представляют собой поперечные волны.
8.
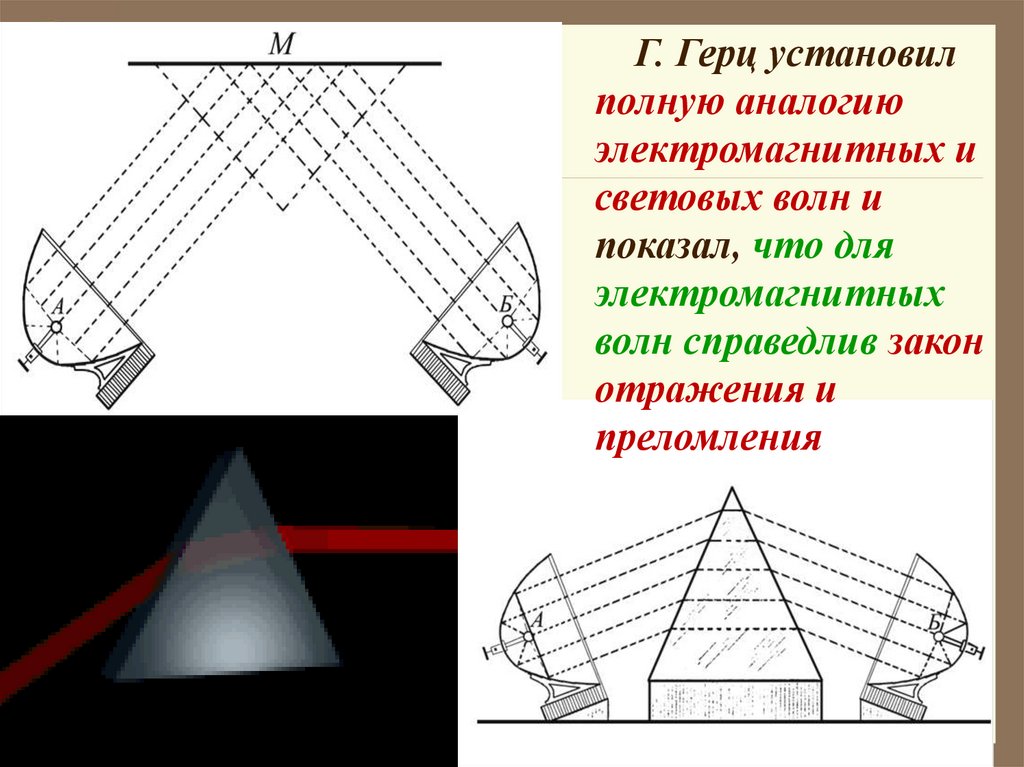
Г. Герц установилполную аналогию
электромагнитных и
световых волн и
показал, что для
электромагнитных
волн справедлив закон
отражения и
преломления
9.
Оптический диапазон длин волнограничен с одной стороны рентгеновскими
лучами, а с другой – микроволновым диапазоном
радиоизлучения. Видимый свет (в вакууме): λ =
[ 400 нм (фиолетовый) − 760 нм (красный)]
9
10.
Интерференциянаблюдается в результате
наложения
когерентных
волн
линейно
поляризованных в одной плоскости. При этом
происходит либо ослабление, либо усиление
интенсивности
света
в
зависимости
от
соотношения фаз складываемых волн.
Условия интерференции света:
1. Когерентность волн , т. е. у этих волн разность
фаз не зависит от времени ( сохраняется за время
наблюдения). Этому условию удовлетворяют
монохроматические электромагнитные волны,
частоты которых одинаковы.
2. Волны должны быть линейно поляризованы в одной
плоскости.
11.
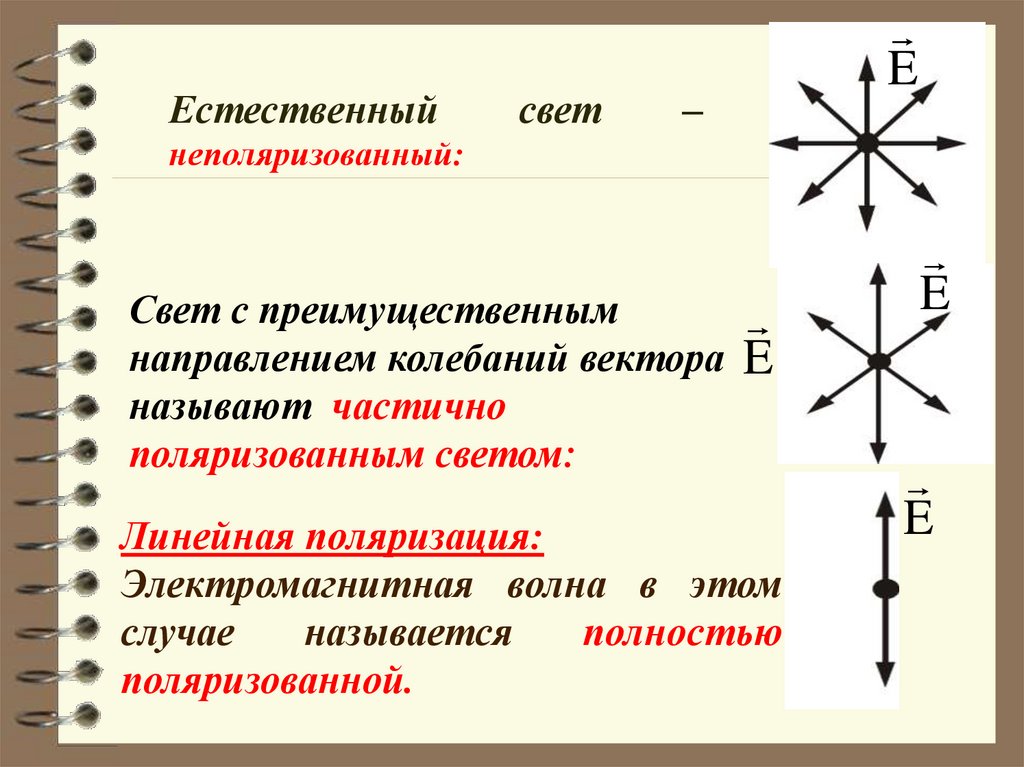
Естественныйсвет
E
–
неполяризованный:
Свет с преимущественным
направлением колебаний вектора
называют частично
поляризованным светом:
E
Линейная поляризация:
Электромагнитная волна в этом
случае
называется
полностью
поляризованной.
E
E
12.
Линейно поляризованная электромагнитная волна иволна круговой поляризации.
13.
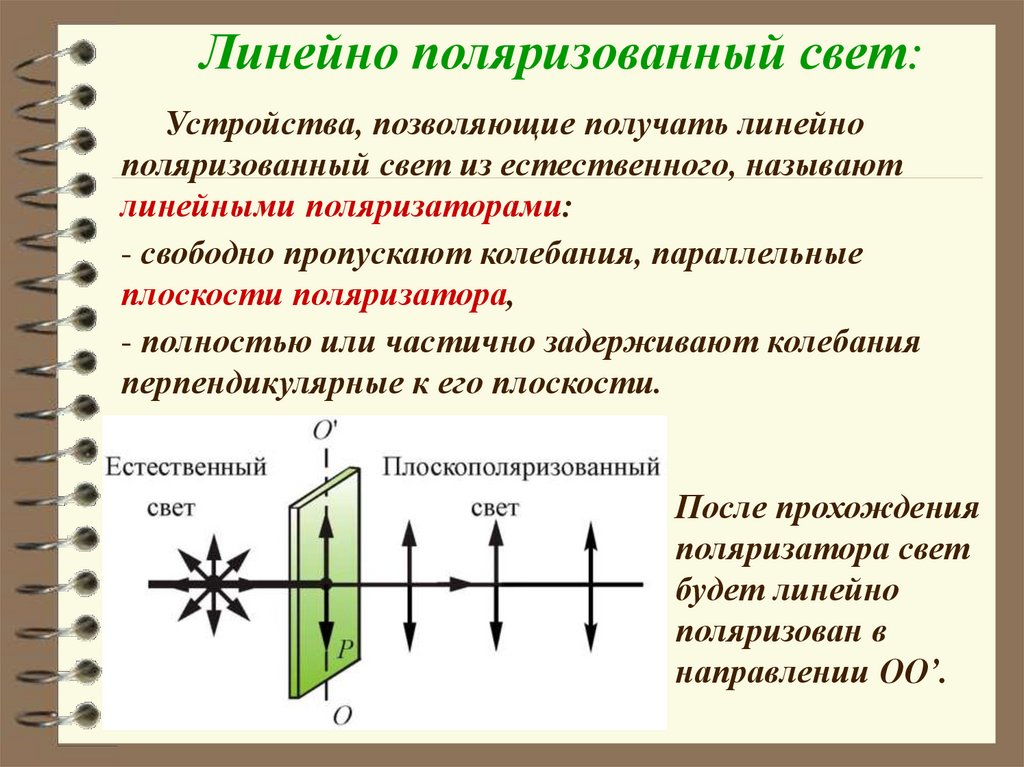
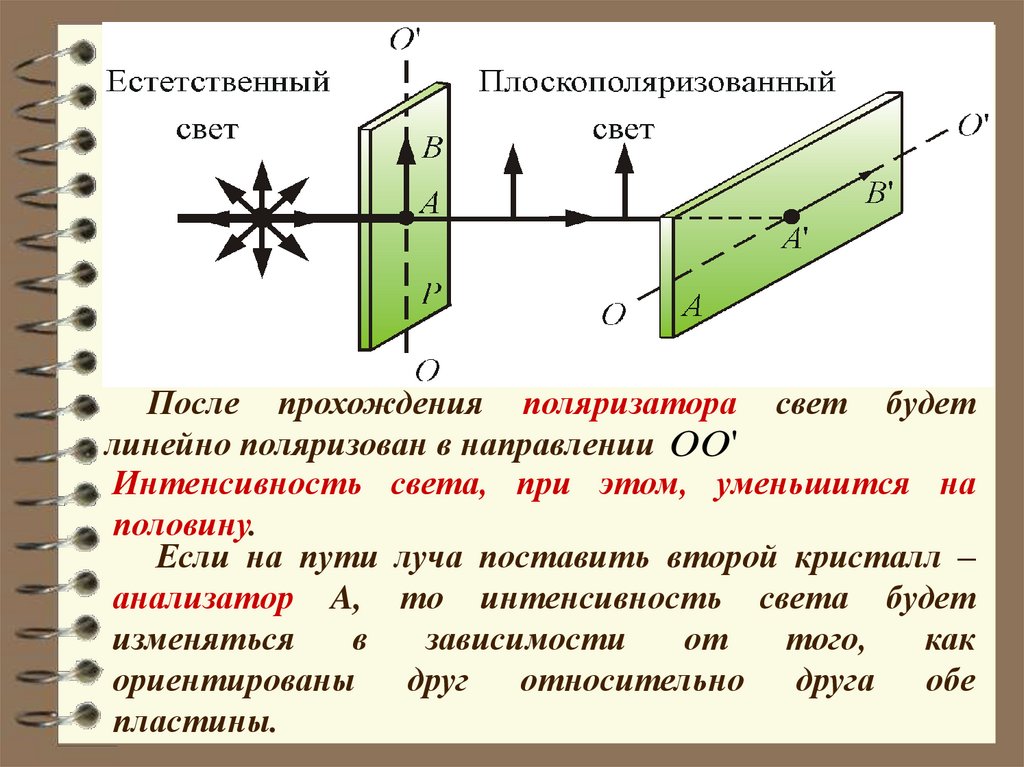
Линейно поляризованный свет:Устройства, позволяющие получать линейно
поляризованный свет из естественного, называют
линейными поляризаторами:
- свободно пропускают колебания, параллельные
плоскости поляризатора,
- полностью или частично задерживают колебания
перпендикулярные к его плоскости.
После прохождения
поляризатора свет
будет линейно
поляризован в
направлении ОО’.
14.
После прохождения поляризатора свет будетлинейно поляризован в направлении OO'
Интенсивность света, при этом, уменьшится на
половину.
Если на пути луча поставить второй кристалл –
анализатор A, то интенсивность света будет
изменяться
в
зависимости
от
того,
как
ориентированы
друг
относительно
друга
обе
пластины.
15.
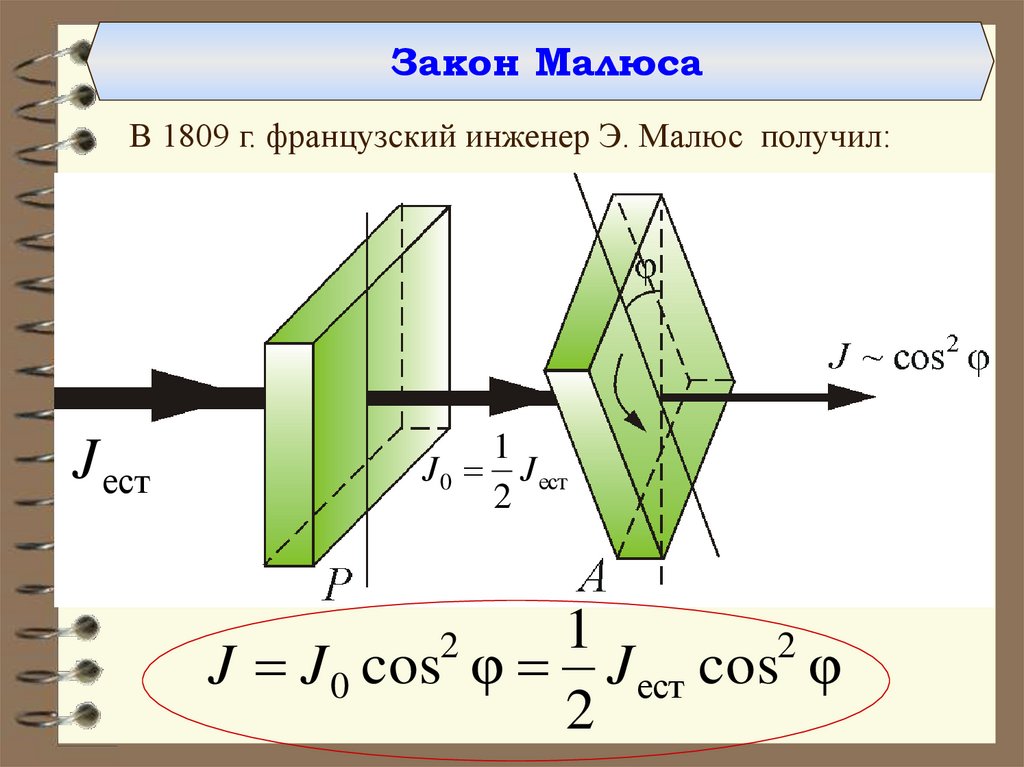
Закон МалюсаВ 1809 г. французский инженер Э. Малюс получил:
J ест
1
J 0 J ест
2
1
2
J J 0 cos φ J ест cos φ
2
2
16.
Прохождение линейно поляризованного света He-Ne лазера черезвращающийся поляроид:
Когда направление выделенной оси поляроида совпадает с
направлением поляризации падающего света, на экране за
поляроидом видно пятно с максимальной интенсивностью.
Когда эти направления перпендикулярны, свет полностью
поглощается поляроидом, и световое пятно на экране отсутствует.
17.
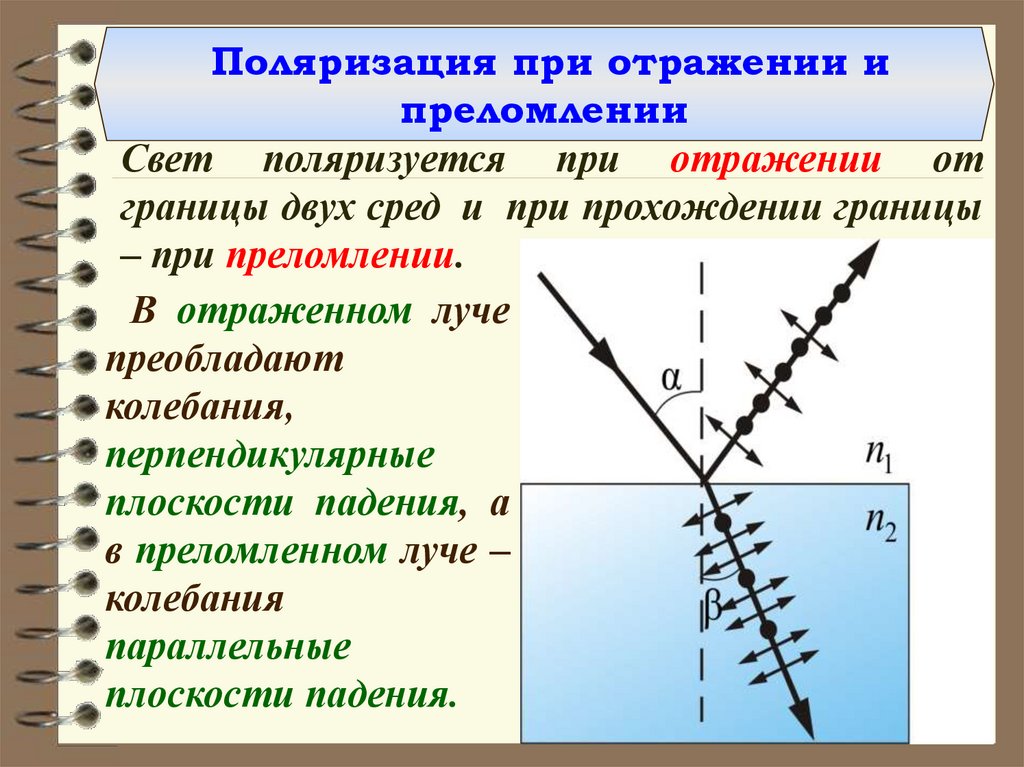
Поляризация при отражении ипреломлении
Свет поляризуется при отражении от
границы двух сред и при прохождении границы
– при преломлении.
В отраженном луче
преобладают
колебания,
перпендикулярные
плоскости падения, а
в преломленном луче –
колебания
параллельные
плоскости падения.
17
18.
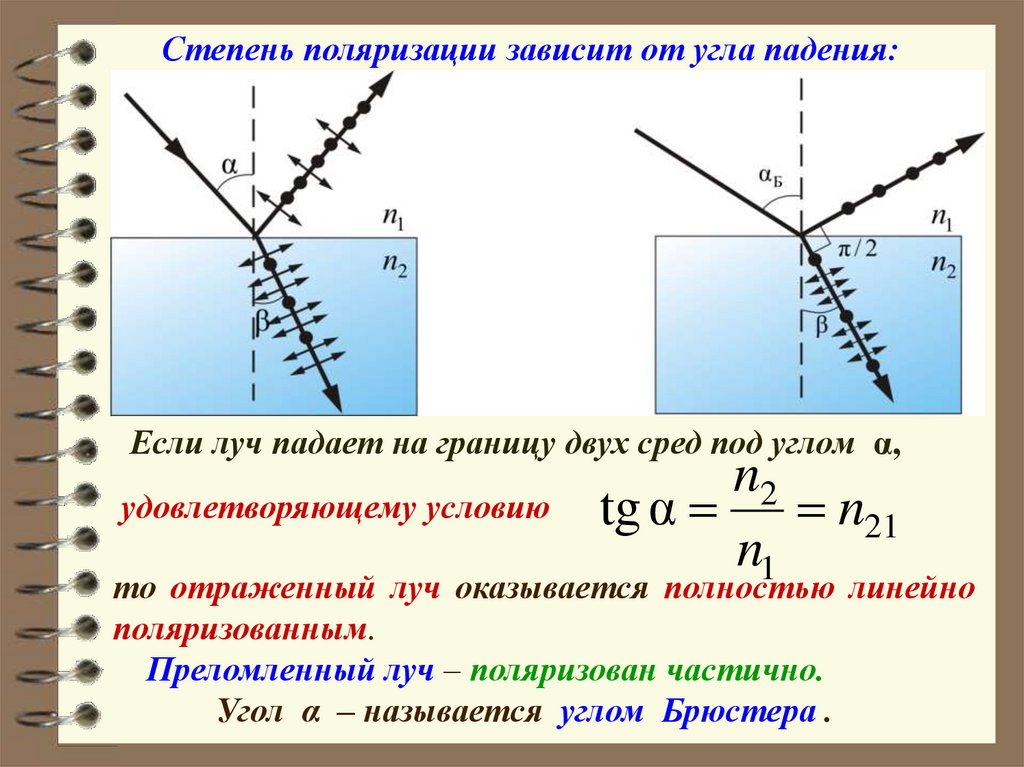
Степень поляризации зависит от угла падения:Если луч падает на границу двух сред под углом α,
n2
удовлетворяющему условию tg α
n21
n1
то отраженный луч оказывается полностью линейно
поляризованным.
Преломленный луч – поляризован частично.
Угол α – называется углом Брюстера .
19.
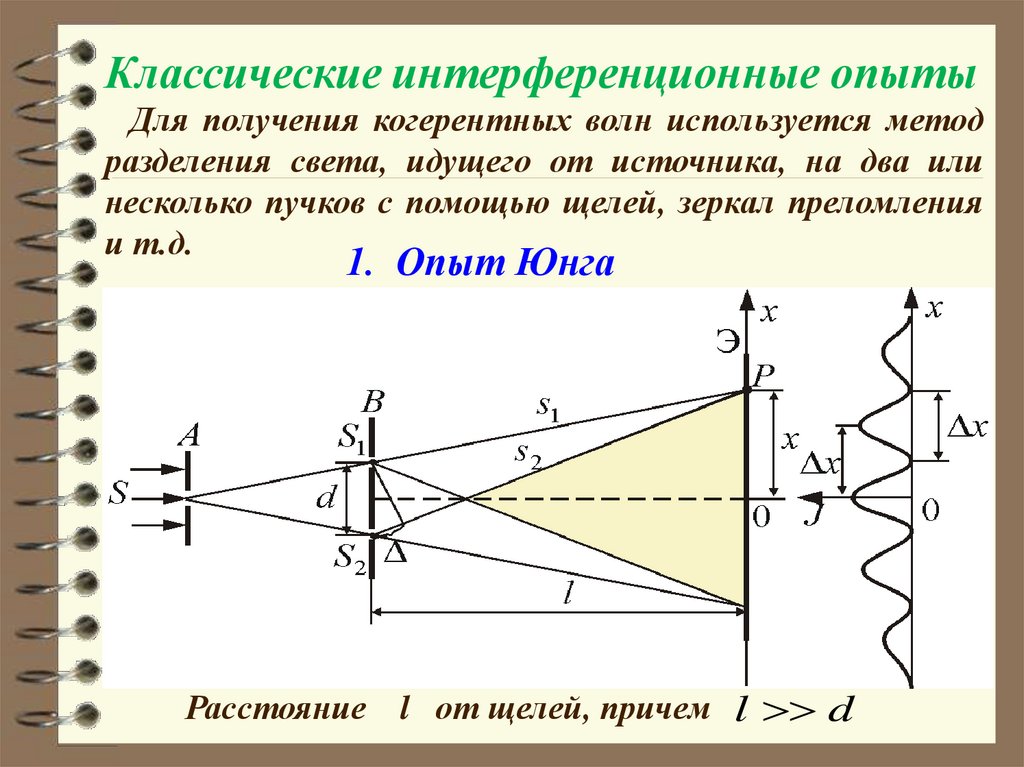
Классические интерференционные опытыДля получения когерентных волн используется метод
разделения света, идущего от источника, на два или
несколько пучков с помощью щелей, зеркал преломления
и т.д.
1. Опыт Юнга
Расстояние
l от щелей, причем l d
20.
Классический интерференционный опыт ЮнгаПараллельный пучок света падает на экран с небольшим
отверстием. Пройдя через отверстие, свет доходит до второго
экрана, в котором проделаны две щели. Когерентные пучки,
излучаемые каждой из щелей, интерферируют на третьем экране.
21.
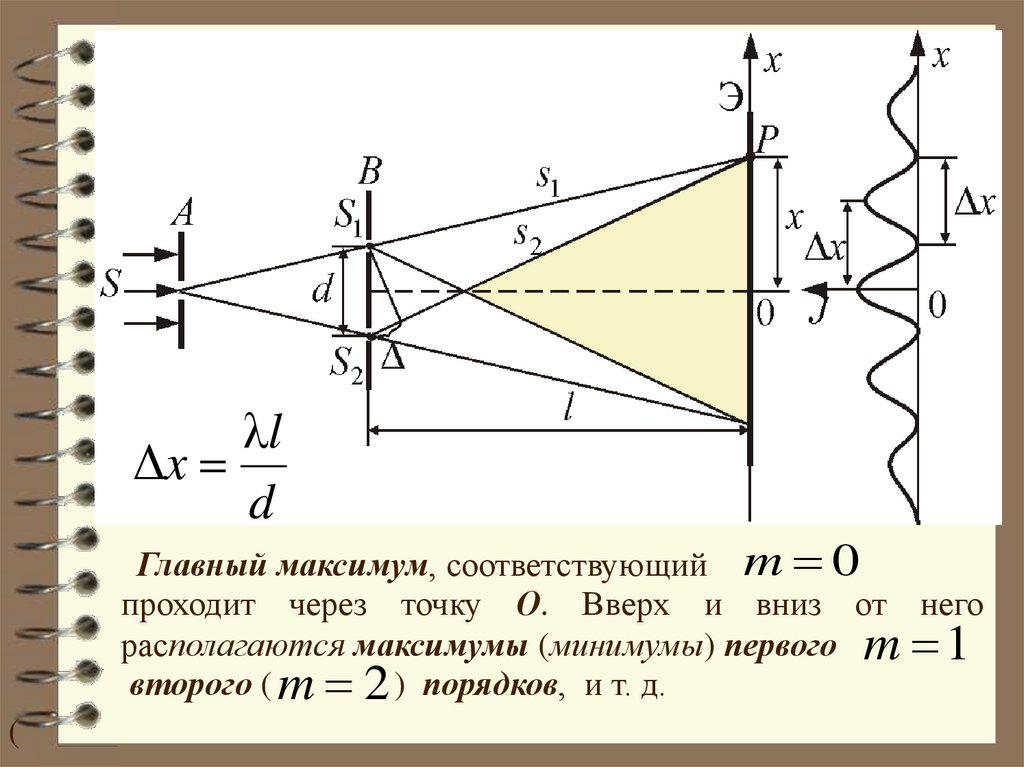
λlΔx
d
Главный максимум, соответствующий m 0
проходит через точку О. Вверх и вниз от него
располагаются максимумы (минимумы) первого m 1
второго ( m 2 ) порядков, и т. д.
(
22.
2223.
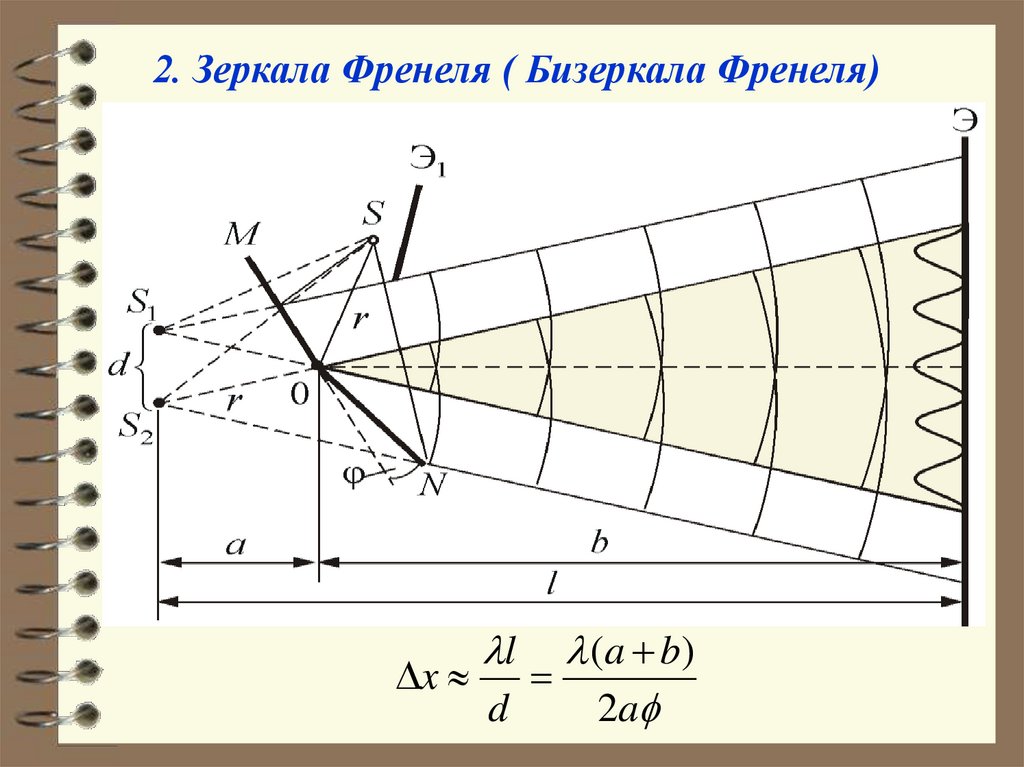
2. Зеркала Френеля ( Бизеркала Френеля)))
l
( a b)
x
d
2a
24.
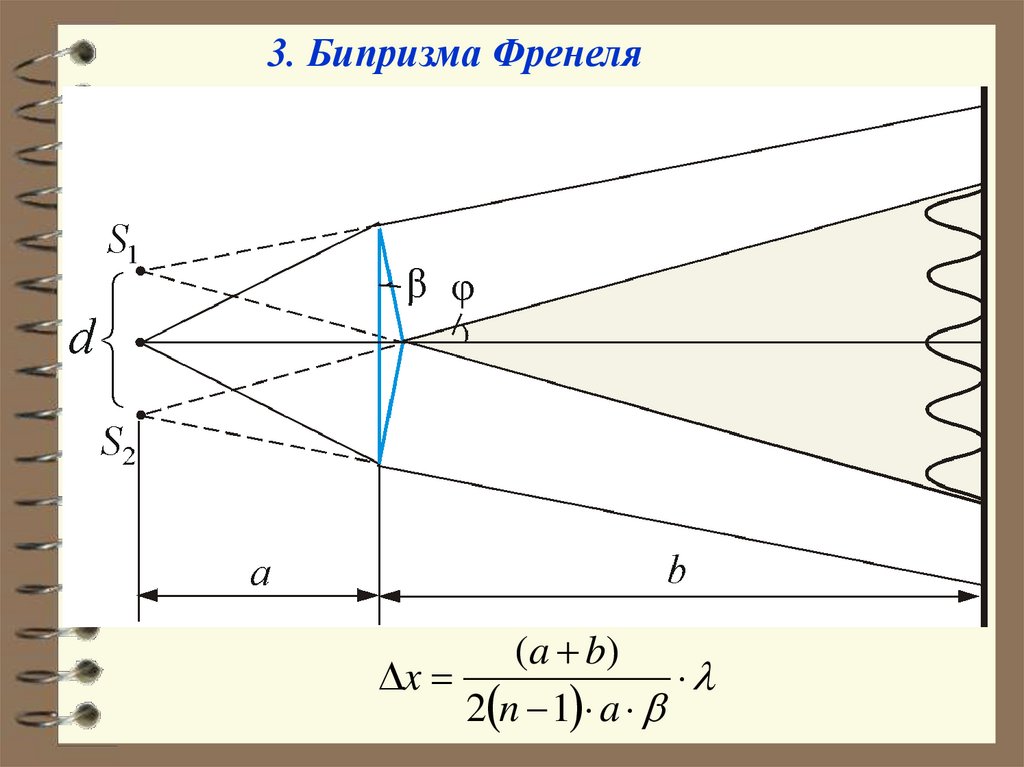
3. Бипризма Френеля( a b)
x
2 n 1 a
25.
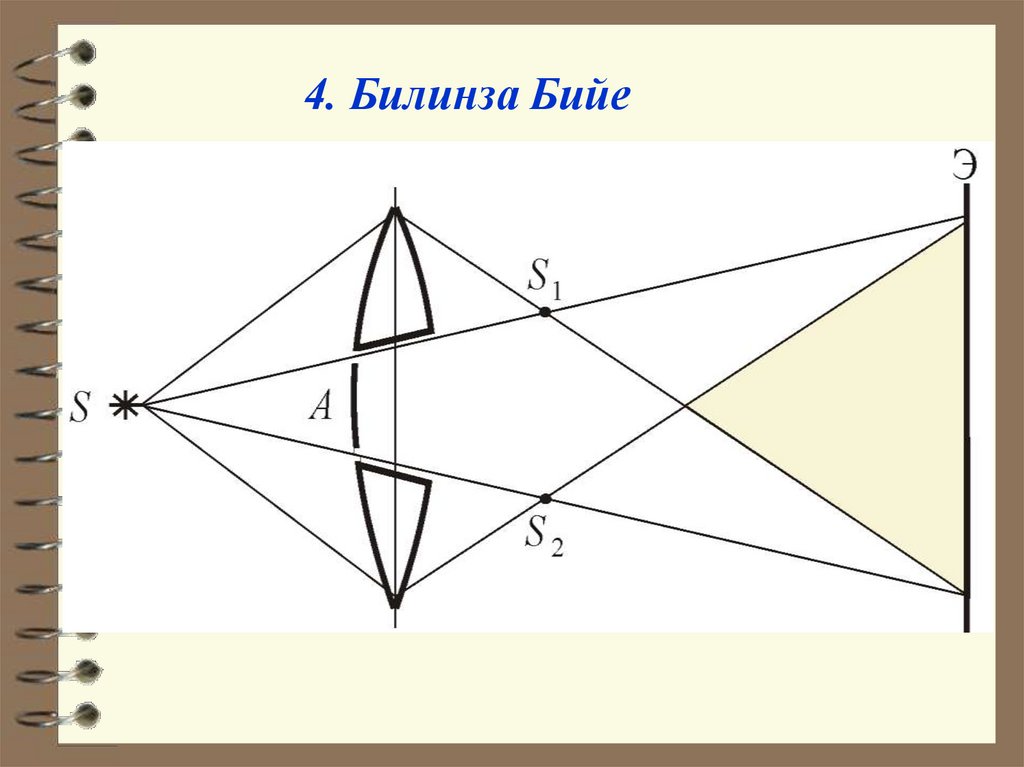
4. Билинза Бийе26.
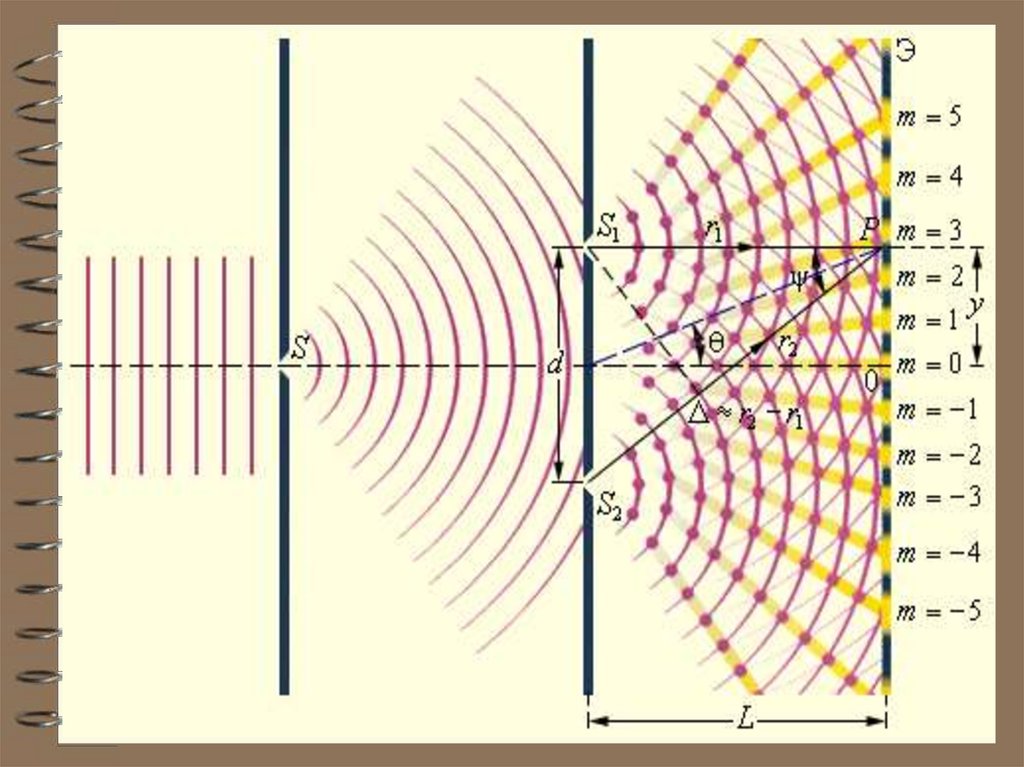
Интерференция двух монохроматических сферических волнПринципиальная схема установок, в которых свет от источника S расщепляется на две когерентные волны с помощью зеркал,
призм, линз и т.п. S1 и S 2 - точечные источники когерентных
волн ( действительные или мнимые).
В
опыте
Юнга
источниками
когерентных
волн
являются
два
отверстия (щели) в
непрозрачном экране,
на которые падает
свет
от
одного
источника.
Расстояние между
отверстиями d не
может
быть
большим
иначе
нарушится условие
когерентности волн.
27.
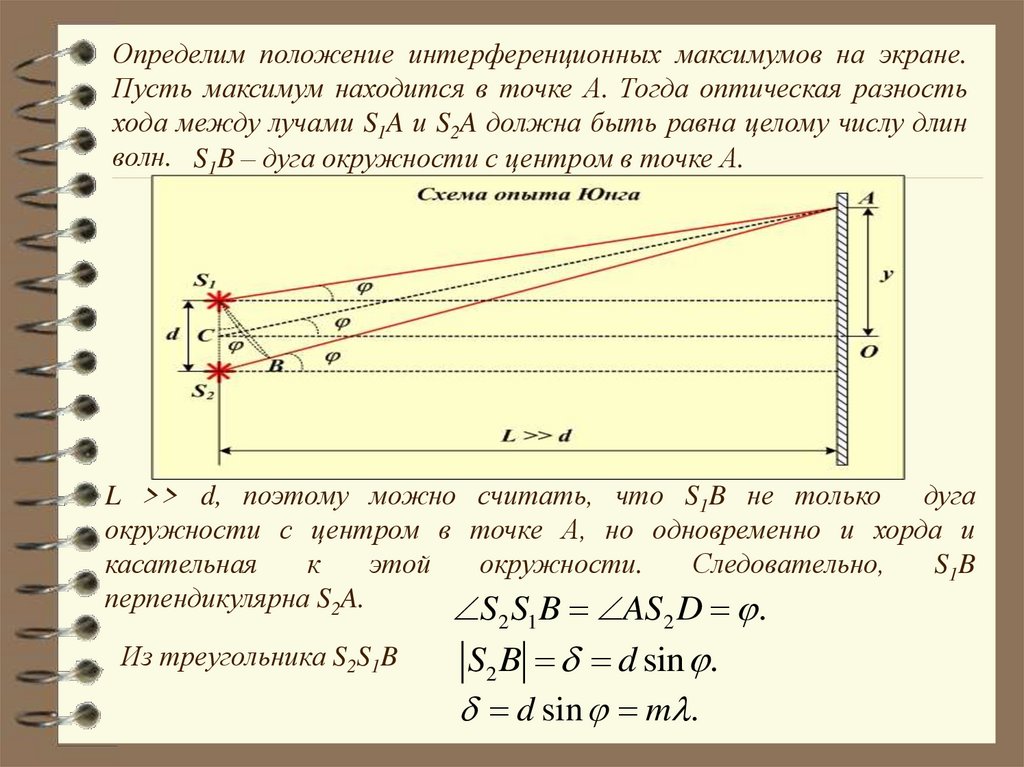
Определим положение интерференционных максимумов на экране.Пусть максимум находится в точке А. Тогда оптическая разность
хода между лучами S1A и S2A должна быть равна целому числу длин
волн. S1B – дуга окружности с центром в точке А.
L >> d, поэтому можно считать, что S1B не только дуга
окружности с центром в точке А, но одновременно и хорда и
касательная
к
этой
окружности.
Следовательно,
S1B
перпендикулярна S2A.
S S B AS D .
2 1
Из треугольника S2S1B
2
S2 B d sin .
d sin m .
28.
Определим положение интерференционных минимумов на экране.Пусть минимум находится в точке А. Тогда оптическая разность
хода между лучами S1A и S2A должна быть равна нечётному числу
длин полуволн.
d sin 2m 1 .
2
Итак, условия
наблюдения
интерференционных
максимумов и
минимумов в опыте
Юнга:
Ì àêñèì óì :
d sin m ,
Ì èí èì óì :
d sin 2m 1 .
2
29.
Интерференция световых волнВолновые свойства света наиболее отчетливо
обнаруживают себя в интерференции и дифракции.
Пусть две волны одинаковой частоты, накладываясь
друг на друга, возбуждают в некоторой точке
пространства колебания одинакового направления:
x1 A1 cos( ωt φ1 )
x2 A2 cos( ωt φ 2 )
30.
Интенсивность световой волны I равна квадратуамплитуды А. Тогда суммарная интенсивность:
I I1 I 2 2 I1I 2 cos( 2 1 )
Последнее слагаемое в этом выражении
2 I1I 2 cos( 2 1 )
-интерференционный член.
В случае когерентных волн
cos( φ 2 φ1 ) const
cos( φ 2 φ1 ) 0 ; I I1 I 2
в максимуме
cos( 2 1 ) 1
I 4I1
cos( φ 2 φ1 ) 0 , интенсивность I I1 I 2
в минимуме
cos( 2 1 ) 1
I 0
31.
Интенсивность результирующей волны от двухточечных источников в точке наблюдения А будет
( при I1 = I2 = I0 ):
I p 2I 0 1 cos k r1 r2 02 01
т.к.
сos k r1 r2 cos k r2 r1
и источники синфазны, то
I p 2 I 0 1 cos kd sin
32.
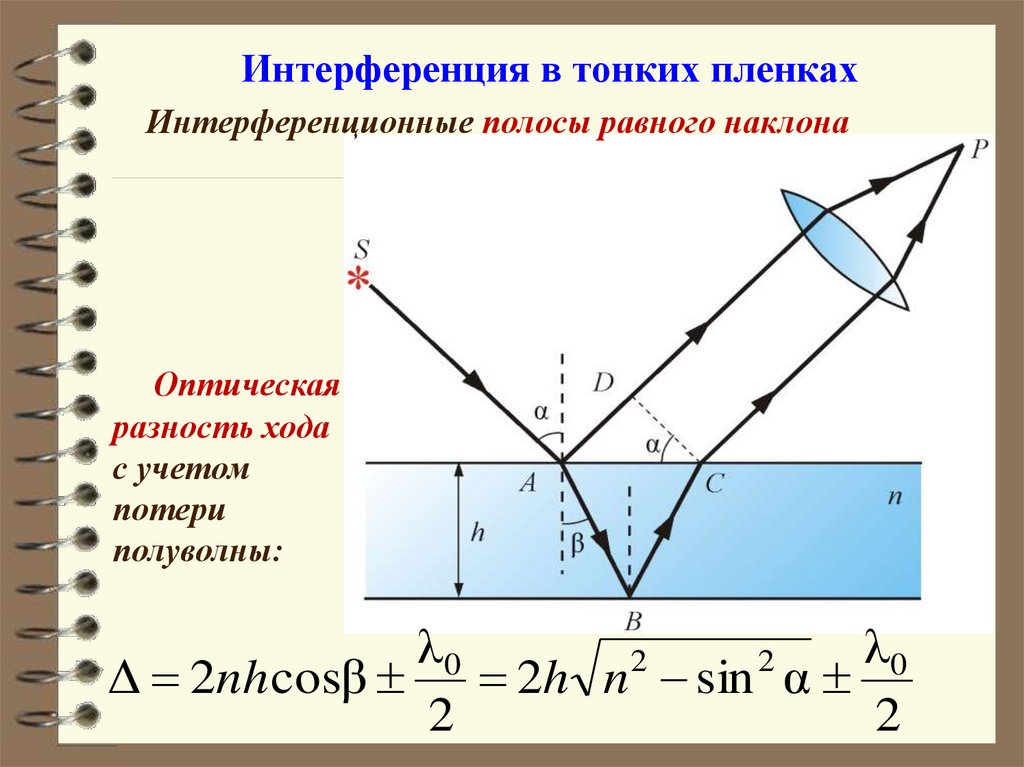
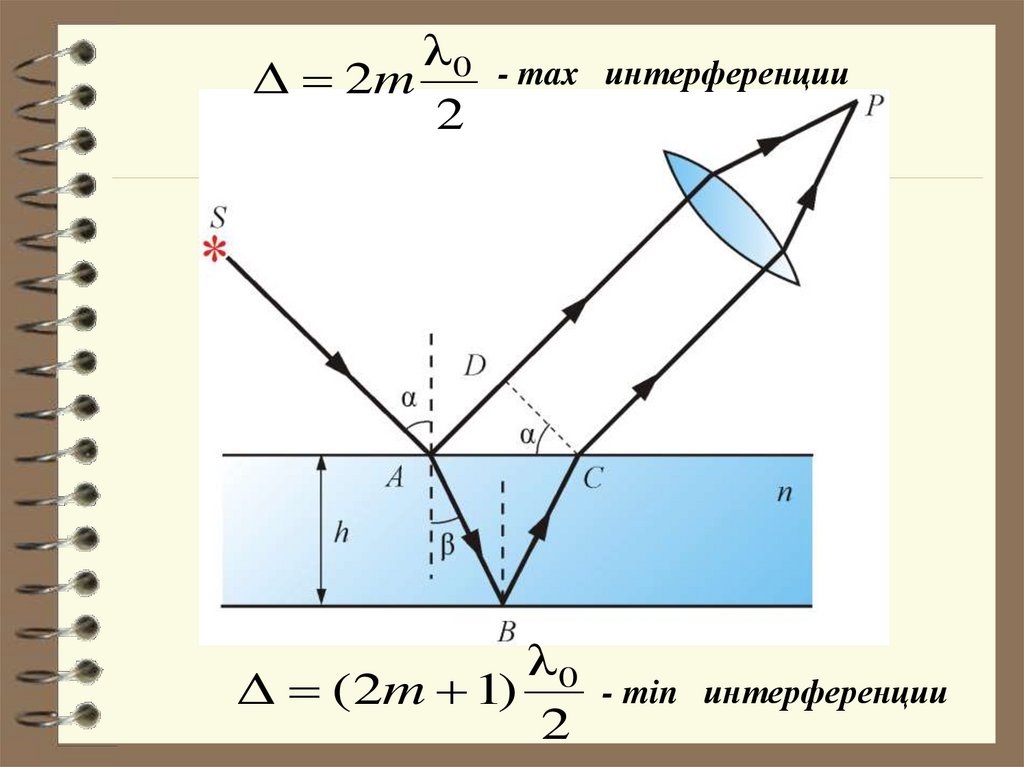
Интерференция в тонких пленкахИнтерференционные полосы равного наклона
Оптическая
разность хода
с учетом
потери
полуволны:
λ0
λ0
2
2
Δ 2nh cosβ
2h n sin α
2
2
33.
λ0Δ 2m
2
- max интерференции
λ0
Δ (2m 1)
2
- min интерференции
34.
Полосы равной толщиныВ белом свете интерференционные полосы, при
отражении от тонких пленок - окрашены. Поэтому
такое явление называют цвета тонких пленок. Его
легко наблюдать на мыльных пузырях, на тонких
пленках масла или бензина, плавающих на
поверхности воды, на пленках окислов, возникающих
на поверхности металлов при закалке, и т.п.
35.
36.
37.
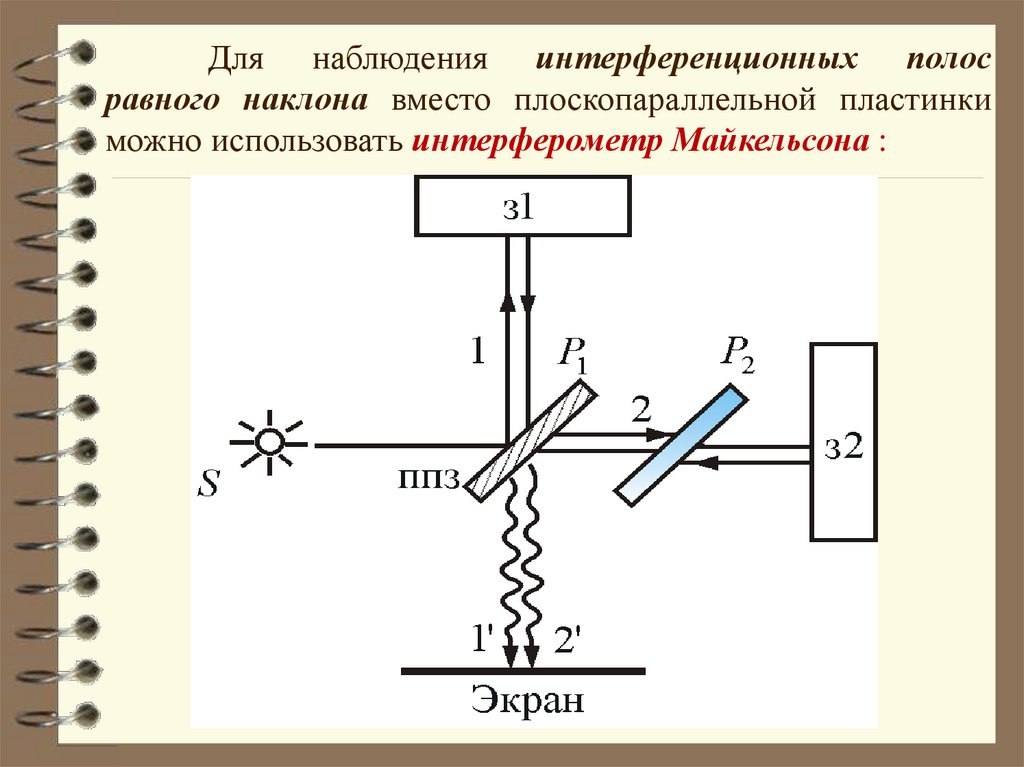
Для наблюдения интерференционных полосравного наклона вместо плоскопараллельной пластинки
можно использовать интерферометр Майкельсона :
38.
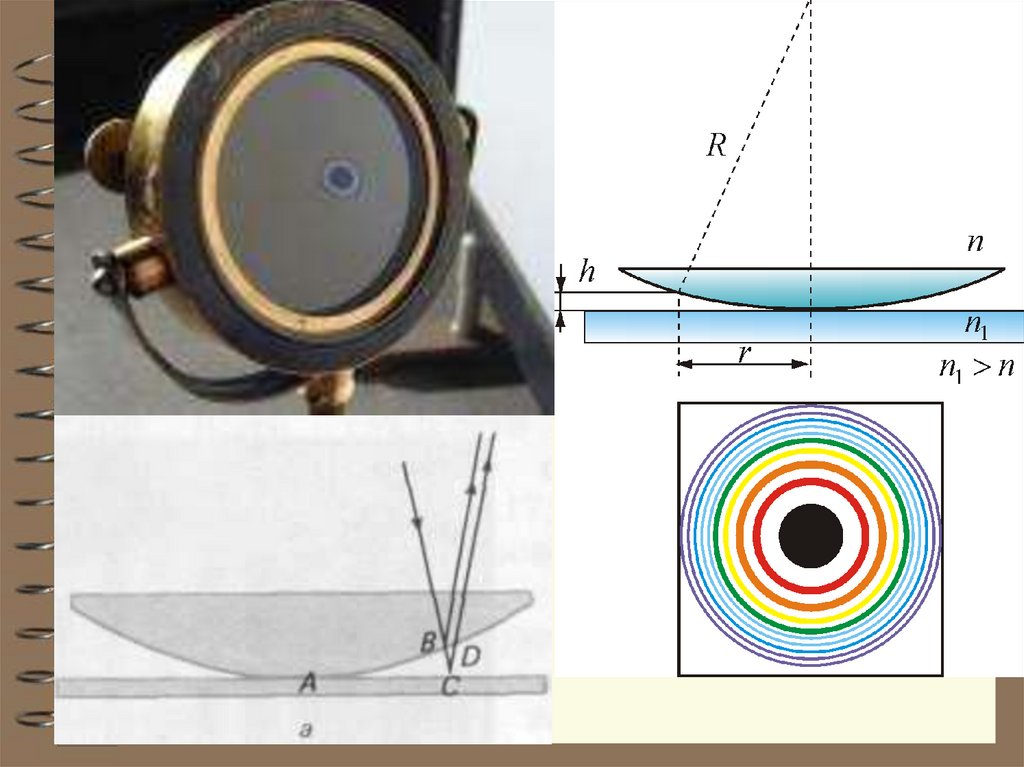
КольцаНьютона
Кольцевые полосы
равной толщины,
наблюдаемые
в
воздушном зазоре
между
соприкасающимися
выпуклой
сферической поверхностью линзы малой
кривизны и плоской поверхностью стекла,
называют кольцами Ньютона.
39.
40. Кольца Ньютона
2r
h R R r
2R
2
2
mλ
h
2
1
rm m λ 0 R
2
- Радиус m-го
светлого кольца
rm mRλ 0
- Радиус m-го темного кольца
41.
Применение интерференции света1. Тот факт, что расположение
интерференционных полос зависит от
длины волны и разности хода лучей,
позволяет по виду интерференционной
картины (или их смещению) проводить
точные измерения расстояний при
известной длине волны или, наоборот,
определять спектр интерферирующих волн
(интерференционная спектроскопия).
42.
2. По интерференционной картине можно выявлять иизмерять неоднородности среды (в т.ч. фазовые), в
которой распространяются волны, или отклонения
формы поверхности от заданной.
43.
3. Явление интерференции волн, рассеянных отнекоторого объекта (или прошедших через
него), с «опорной» волной лежит в основе
голографии (в т.ч. оптической, акустической
или СВЧ-голографии).
44.
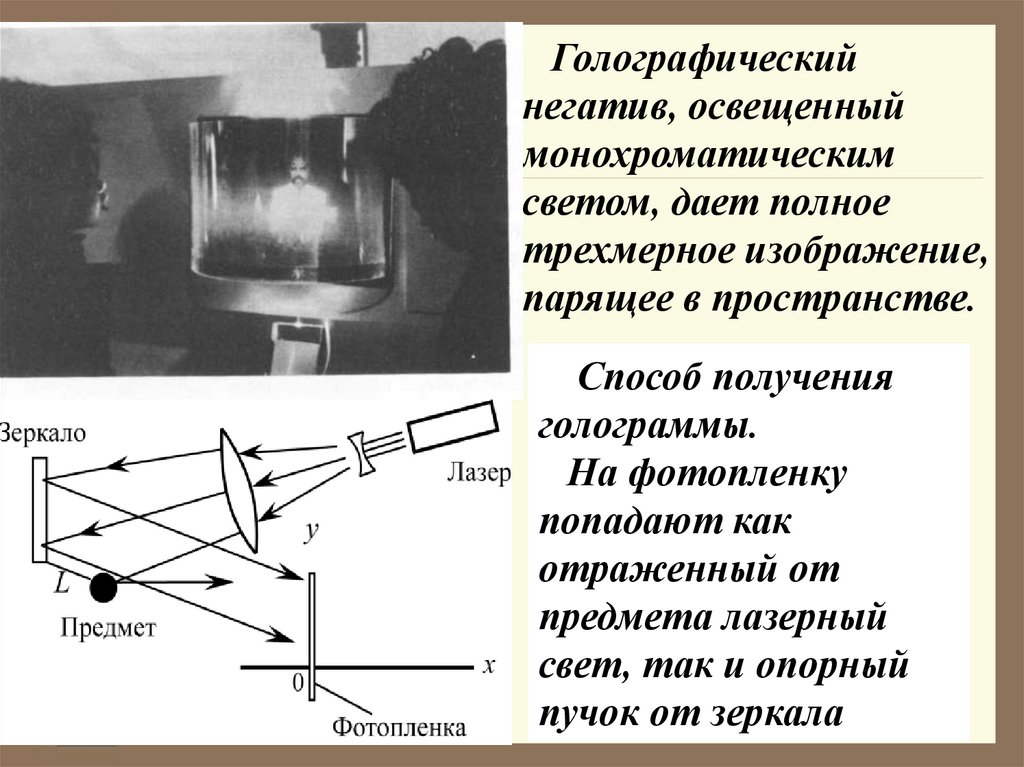
Голографическийнегатив, освещенный
монохроматическим
светом, дает полное
трехмерное изображение,
парящее в пространстве.
Способ получения
голограммы.
На фотопленку
попадают как
отраженный от
предмета лазерный
свет, так и опорный
пучок от зеркала




























 physics
physics








