Решение систем линейных уравнений

1. Тема 4

Решение систем линейных
уравнений.

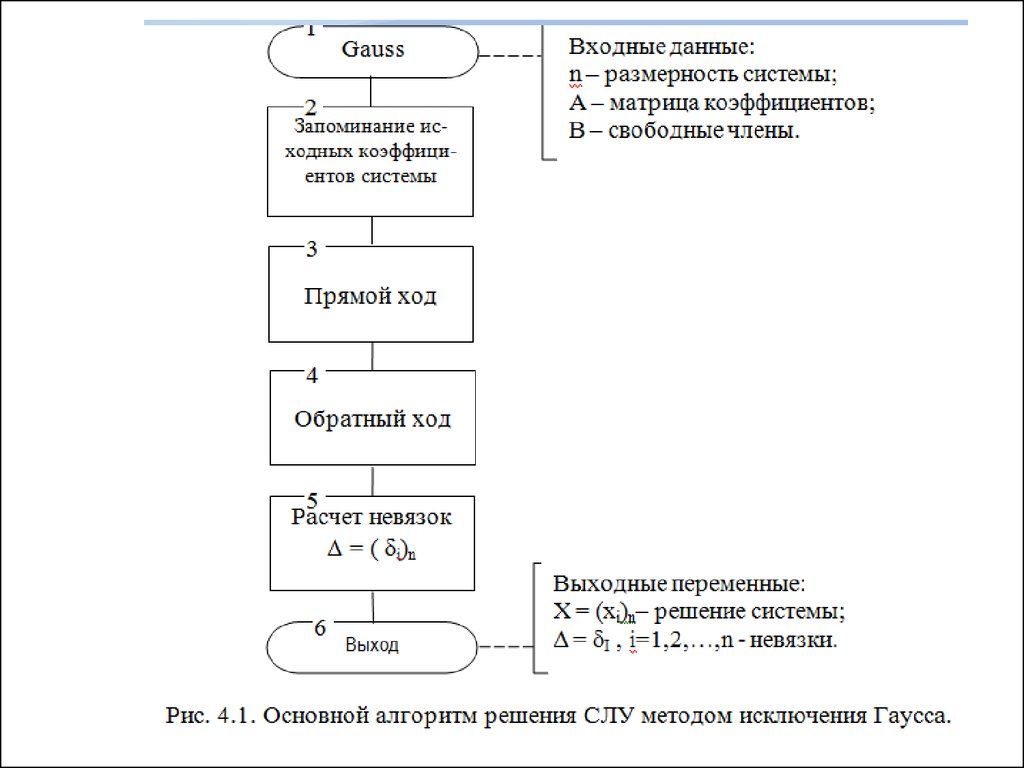
2.

3.

4.

5.

6.

7.

8.

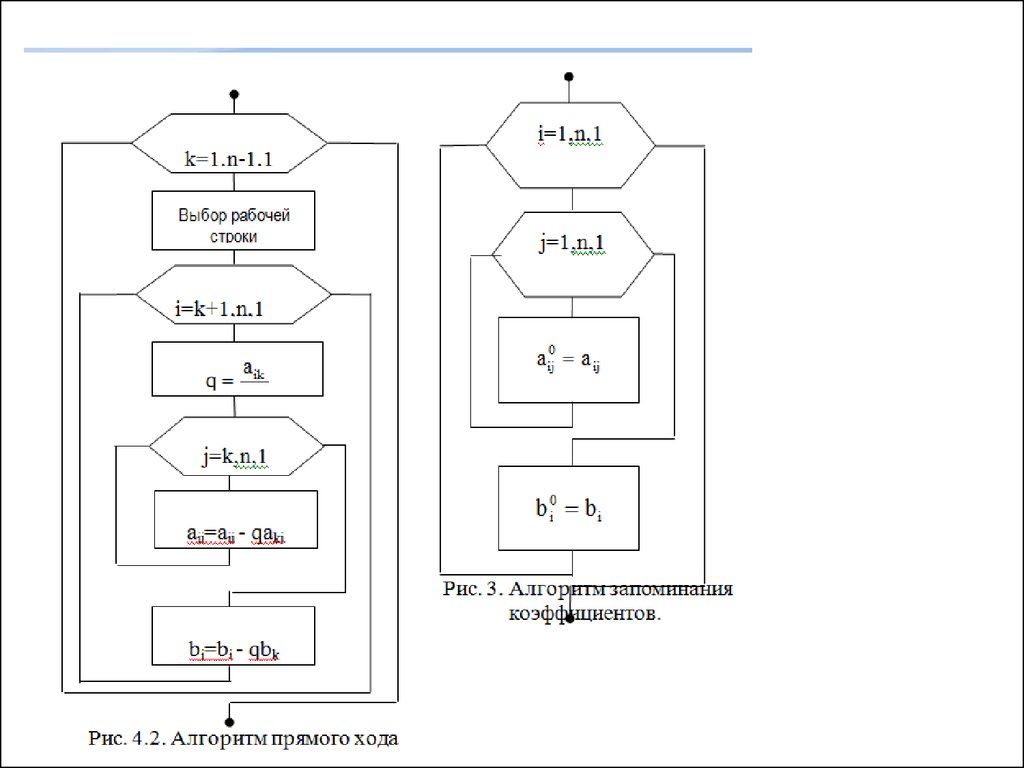
9.

10.

2 1 – 0 – 3 (-1) = 5
Система обращается в тождество, решение
верное.
Формулы Крамера применяться редко, только для
n≤4.

11. 4.2. Метод исключений Гаусса.

12.

13.

14.

15.

16.

17.

18.

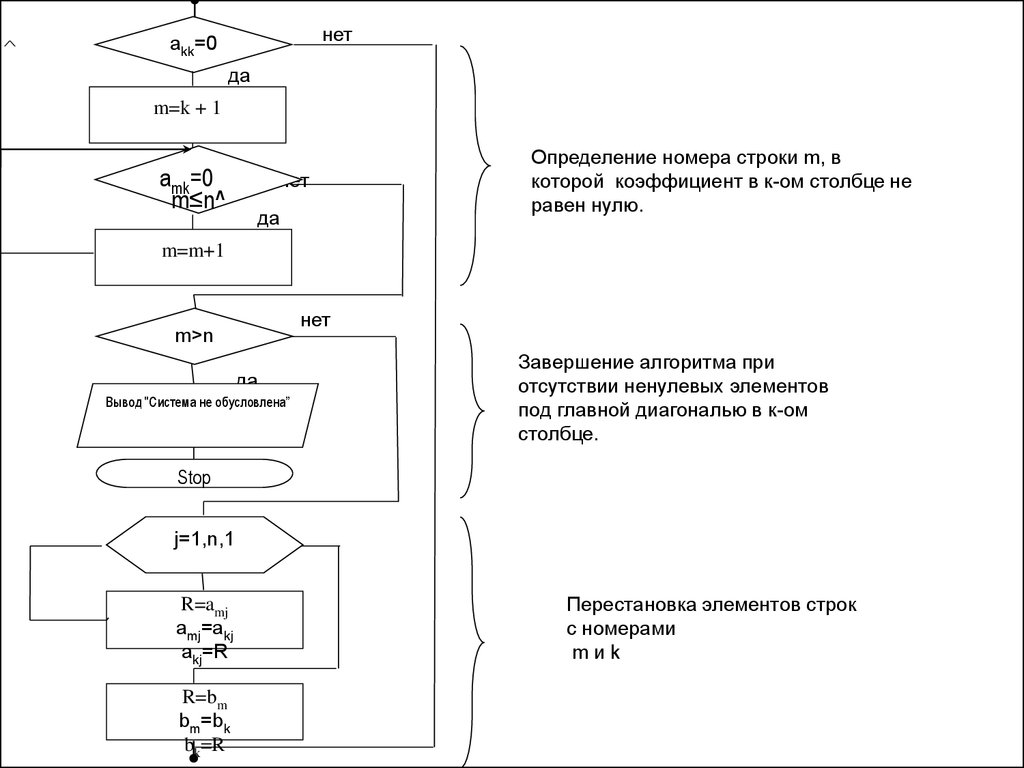
нет
akk=0
да
m=k + 1
amk=0
m≤n^
нет
да
Определение номера строки m, в
которой коэффициент в к-ом столбце не
равен нулю.
m=m+1
нет
m>n
да
Вывод "Система не обусловлена”
Завершение алгоритма при
отсутствии ненулевых элементов
под главной диагональю в к-ом
столбце.
Stop
j=1,n,1
R=amj
amj=akj
akj=R
R=bm
bm=bk
bk=R
Перестановка элементов строк
с номерами
mиk

19.

Рис. 4.5. Алгоритм выбора рабочей строки.

20.

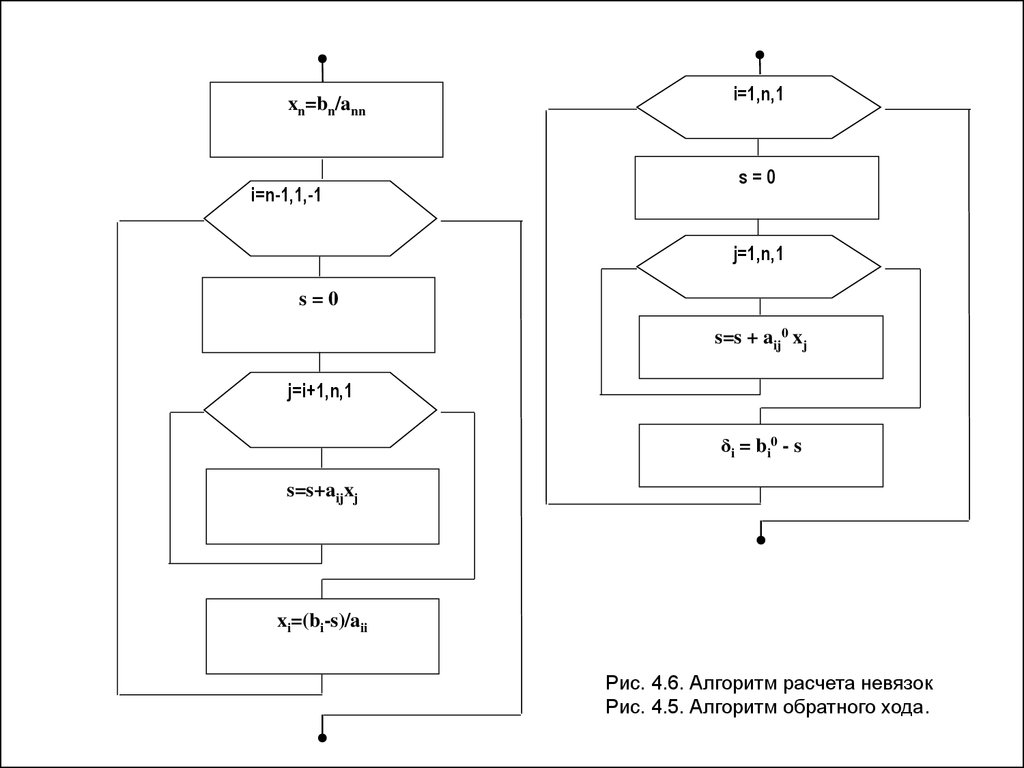
xn=bn/ann
i=n-1,1,-1
i=1,n,1
s=0
j=1,n,1
s=0
s=s + aij0 xj
j=i+1,n,1
δi = bi0 - s
s=s+aijxj
xi=(bi-s)/aii
Рис. 4.6. Алгоритм расчета невязок
Рис. 4.5. Алгоритм обратного хода.

21.

Нужно подчеркнуть, что для вычисления
значения определителя квадратной матрицы
можно использовать алгоритм прямого хода: для
треугольной или диагональной квадратной
матрицы определитель равен произведению
элементов главной диагонали.

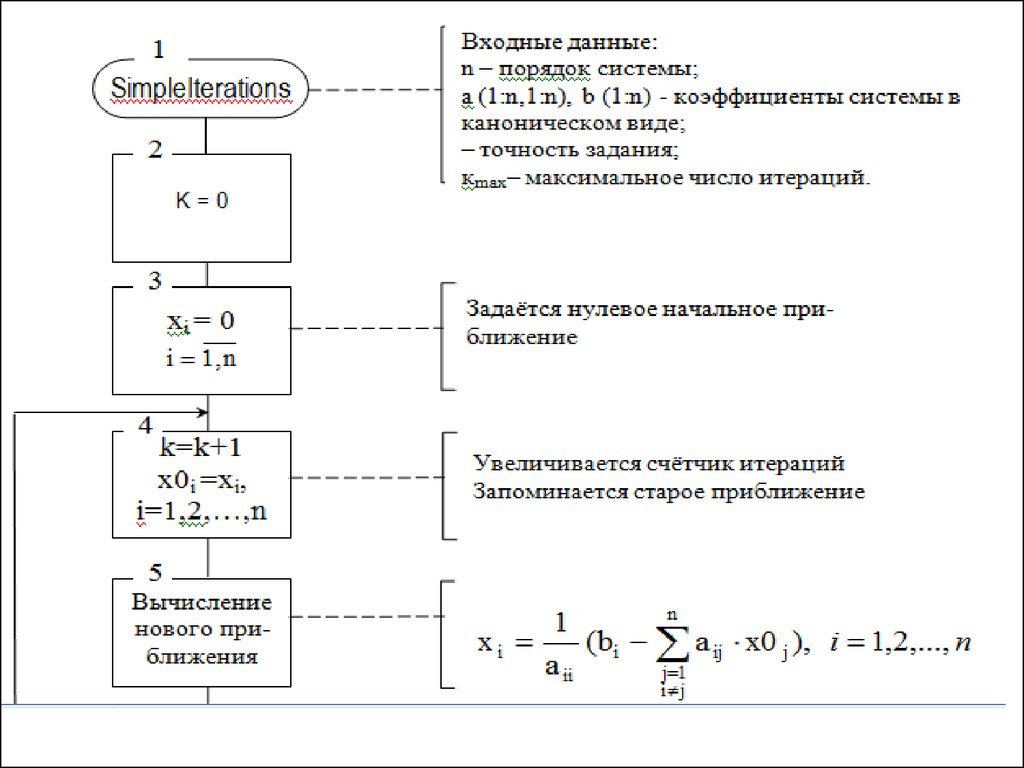
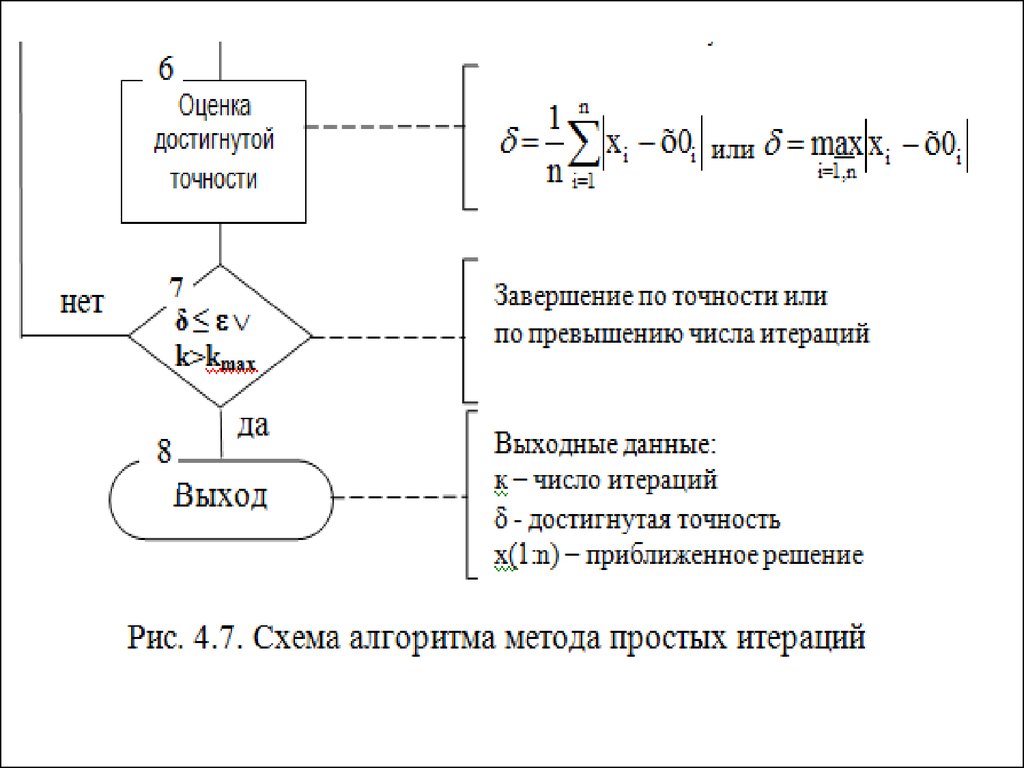
22. 4.3. Метод простых итераций.

23.

24.

25.

26.

27.

28. 4.4 Метод Гаусса-Зейделя  

4.4 Метод Гаусса-Зейделя

29.

30.

Недостаток - не всегда можно обеспечить
сходность итерационного процесса. С
увеличением размерности системы труднее
выполнить линейные преобразования для
обеспечения сходимости.