Возрастание и убывание функций

1.

2.

Если производная дифференцируемой
функции положительна внутри
некоторого промежутка Х, то функция
возрастает на этом промежутке.

3.

Рассмотрим значения х1 и х2, принадлежащие
промежутку Х.
Пусть x2 x1
Для функции f(x) на отрезке [x1;x2] выполняется
теорема Лагранжа:
где
f ( x2 ) f ( x1 ) f ( ) ( x2 x1 )
x1 x2
Т.е. ξ принадлежит промежутку, на котором
производная функции положительна:

4.

f ( ) 0
и правая часть последнего равенства тоже будет
положительна:
f ( ) ( x2 x1 ) 0
Тогда левая часть тоже будет положительна:
f ( x2 ) f ( x1 ) 0
То есть
f ( x2 ) f ( x1 )
Получили, что большему значению аргумента
соответствует большее значение функции.
Это означает, что функция возрастает.

5.

Если производная дифференцируемой
функции отрицательна внутри
некоторого промежутка Х, то она
убывает на этом промежутке.

6.

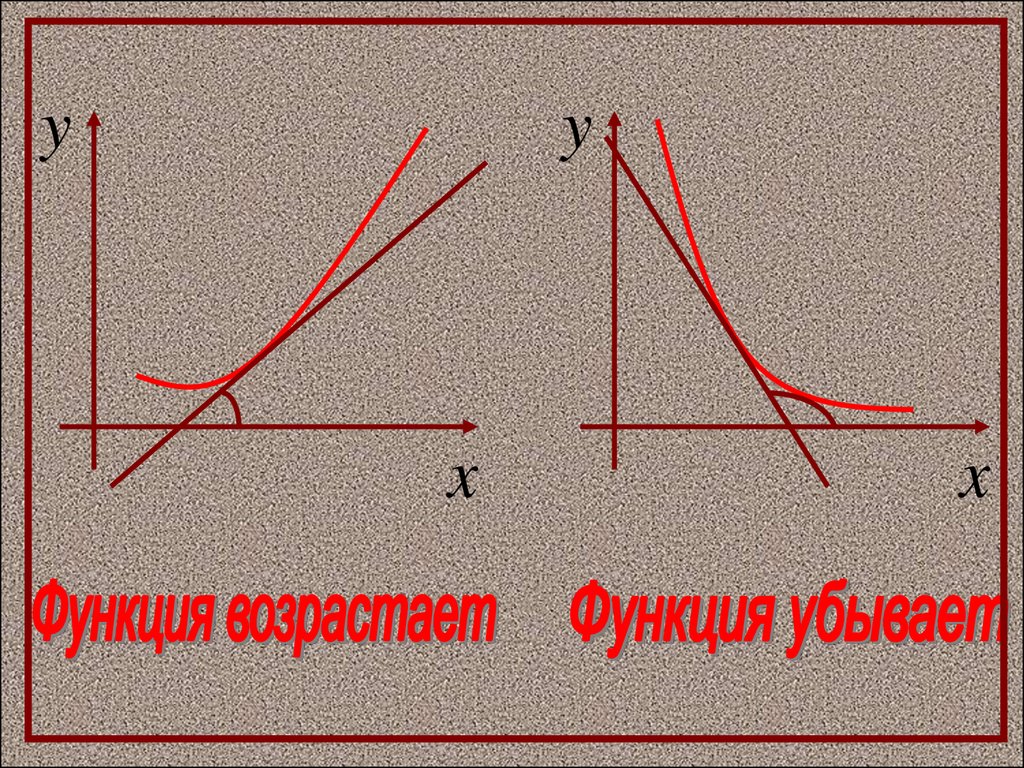
Если касательные к кривой на некотором
промежутке направлены под острыми
углами к оси х, то функция возрастает.
если они направлены под тупыми углами,
то функция убывает.

7.

y
y
x
x

8.

Найти интервалы монотонности
функции
y x 4x 3
2

9.

Найдем производную этой функции:
y ( x 4x 3) 2x 4
2
Исследуем знак этой производной:
y 2 x 4 0 при
x 2
y 2 x 4 0
x 2
при
Следовательно, функция будет возрастать на
промежутке ( 2 ; )
Функция будет убывать на промежутке
( ; 2)