Применение нескольких способов разложения на множители

1.

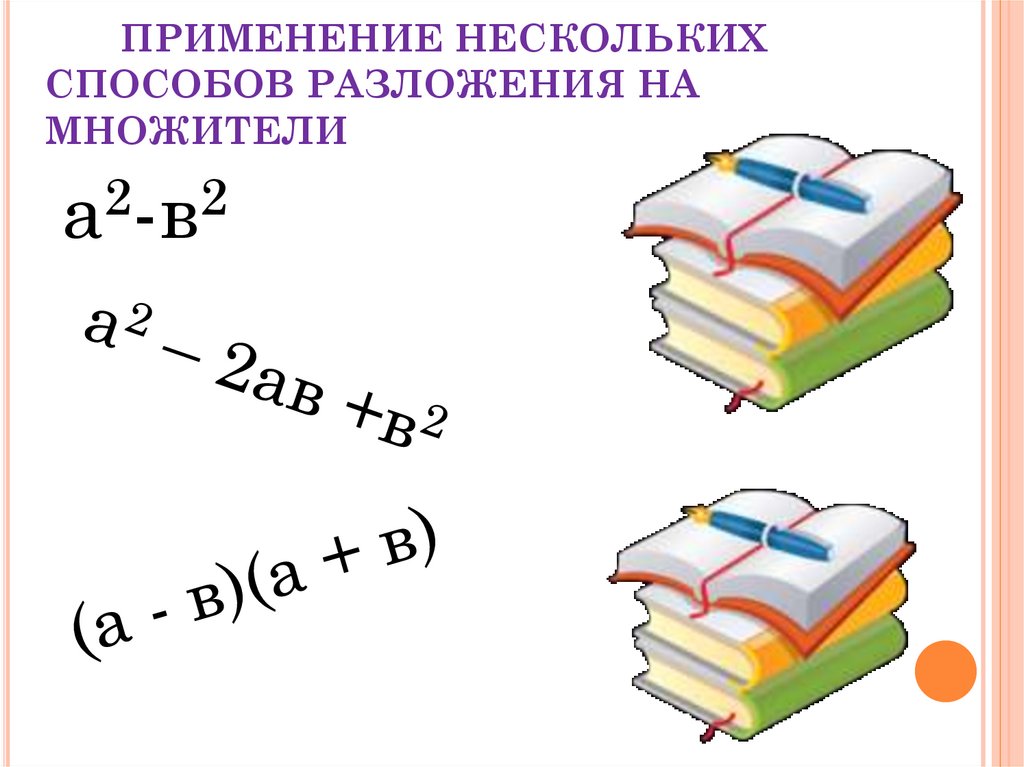
ПРИМЕНЕНИЕ НЕСКОЛЬКИХ
СПОСОБОВ РАЗЛОЖЕНИЯ НА
МНОЖИТЕЛИ
2
2
а -в

2.

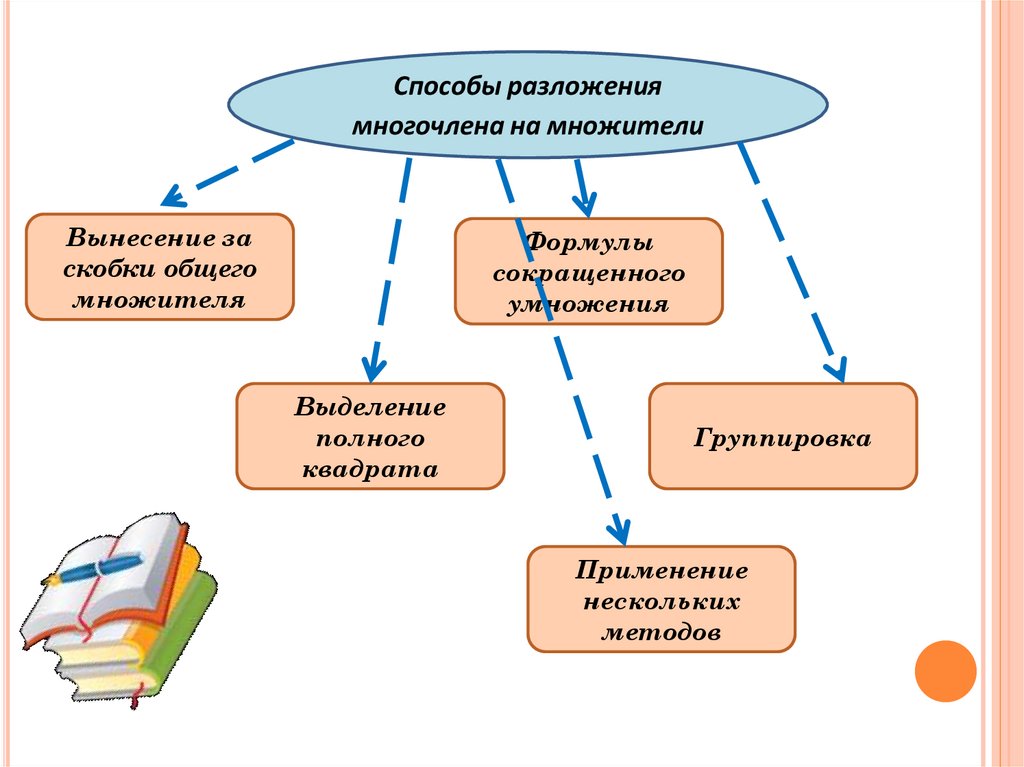
Способы разложения
многочлена на множители
Вынесение за
скобки общего
множителя
Формулы
сокращенного
умножения
Выделение
полного
квадрата
Группировка
Применение
нескольких
методов

3.

ВЫНЕСЕНИЕ ОБЩЕГО
МНОЖИТЕЛЯ ЗА СКОБКУ
а) Найти общий множитель,
б) Каждый член многочлена разделить на этот
множитель
Пример: 24х2у4-16х8у6+8х6у5= 8х2у4(3-2х6у2+х4у)
а) общий множитель: 8х2у4
б) разделим каждое слагаемое на 8х2у4

4.

СПОСОБ ГРУППИРОВКИ:
а) Сгруппировать слагаемые так, чтобы в
каждой группе был общий множитель
б) Вынести этот общий множитель за скобку
так, чтобы в каждой группе был общий
множитель многочлен
в) Вынести за скобку общий множитель –
многочлен
ПРИМЕР:
17а2в – 5ав2+34ав – 10в2=
(17а2в+34ав) - (5ав2+10в2)=
17ав(а+2) – 5в2(а+2)=
(а+2)(17ав-5в2)=в(а+2)(17а-5в)

5.

ФОРМУЛЫ СОКРАЩЁННОГО УМНОЖЕНИЯ
а) Разность квадратов: а2-в2= (а - в)(а + в)
б) Квадрат разности: а2 – 2ав +в2 = (а - в)2
в) Квадрат суммы: а2 + 2ав + в2=(а + в)2

6.

ФОРМУЛЫ СОКРАЩЁННОГО УМНОЖЕНИЯ
а) Разность квадратов: а2-в2= (а - в)(а + в)
б) Квадрат разности: а2 – 2ав +в2 = (а - в)2
в) Квадрат суммы: а2 + 2ав + в2=(а + в)2
Примеры:
16х4 – 0,25у8 =

7.

ФОРМУЛЫ СОКРАЩЁННОГО УМНОЖЕНИЯ
а) Разность квадратов: а2-в2= (а - в)(а + в)
б) Квадрат разности: а2 – 2ав +в2 = (а - в)2
в) Квадрат суммы: а2 + 2ав + в2=(а + в)2
Примеры:
16х4 – 0,25у8 = (4х2 – 0,5у4)(4х2+0,5у4)

8.

ФОРМУЛЫ СОКРАЩЁННОГО УМНОЖЕНИЯ
а) Разность квадратов: а2-в2= (а - в)(а + в)
б) Квадрат разности: а2 – 2ав +в2 = (а - в)2
в) Квадрат суммы: а2 + 2ав + в2=(а + в)2
Примеры:
16х4 – 0,25у8 = (4х2 – 0,5у4)(4х2+0,5у4)
0,36х2 – 2,4ху + 16у2 =

9.

ФОРМУЛЫ СОКРАЩЁННОГО УМНОЖЕНИЯ
а) Разность квадратов: а2-в2= (а - в)(а + в)
б) Квадрат разности: а2 – 2ав +в2 = (а - в)2
в) Квадрат суммы: а2 + 2ав + в2=(а + в)2
Примеры:
16х4 – 0,25у8 = (4х2 – 0,5у4)(4х2+0,5у4)
0,36х2 – 2,4ху + 16у2 = (0,6х – 4у)2 = (0,6х-4у)(0,6х- 4у)

10.

ФОРМУЛЫ СОКРАЩЁННОГО УМНОЖЕНИЯ
а) Разность квадратов: а2-в2= (а - в)(а + в)
б) Квадрат разности: а2 – 2ав +в2 = (а - в)2
в) Квадрат суммы: а2 + 2ав + в2=(а + в)2
Примеры:
16х4 – 0,25у8 = (4х2 – 0,5у4)(4х2+0,5у4)
0,36х2 – 2,4ху + 16у2 = (0,6х – 4у)2 = (0,6х-4у)(0,6х- 4у)
1,44а4 + 2,4а2 +1 =

11.

ФОРМУЛЫ СОКРАЩЁННОГО УМНОЖЕНИЯ
а) Разность квадратов: а2-в2= (а - в)(а + в)
б) Квадрат разности: а2 – 2ав +в2 = (а - в)2
в) Квадрат суммы: а2 + 2ав + в2=(а + в)2
Примеры:
16х4 – 0,25у8 = (4х2 – 0,5у4)(4х2+0,5у4)
0,36х2 – 2,4ху + 16у2 = (0,6х – 4у)2 = (0,6х-4у)(0,6х- 4у)
1,44а4 + 2,4а2 +1 = (1,2а2+1)2 = (1,2а2+1)(1,2а2 +1)

12.

РАЗЛОЖИТЕ НА МНОЖИТЕЛИ
МНОГОЧЛЕН: 5А2 - 20
Вынесем общий множитель за скобку, получим: 5(а2-4)
Что заметили?

13.

РАЗЛОЖИТЕ НА МНОЖИТЕЛИ
МНОГОЧЛЕН: 5А2 - 20
Вынесем общий множитель за скобку, получим: 5(а2-4)
Что заметили?
Многочлен в скобке можно разложить по формуле
разности квадратов 5а2 – 20 = 5(а2 -4) = 5(а - 2)(а + 2)
Какие способы разложения многочлена на множители
вы использовали?

14.

РАЗЛОЖИТЕ НА МНОЖИТЕЛИ
МНОГОЧЛЕН: 5А2 - 20
Вынесем общий множитель за скобку, получим: 5(а2-4)
Что заметили?
Многочлен в скобке можно разложить по формуле
разности квадратов 5а2 – 20 = 5(а2 -4) = 5(а - 2)(а + 2)
Какие способы разложения многочлена на множители
вы использовали? (вынесение общего множителя за
скобки; формула разности квадратов двух выражений).
Чем больше множителей
получиться, тем лучше!

15.

РАЗЛОЖИТЕ МНОГОЧЛЕН НА
МНОЖИТЕЛИ
18х2+12х+2

16.

РАЗЛОЖИТЕ МНОГОЧЛЕН НА
МНОЖИТЕЛИ
18х2+12х+2
Вынесем общий множитель за скобку
2(9х2+6х+1)

17.

РАЗЛОЖИТЕ МНОГОЧЛЕН НА
МНОЖИТЕЛИ
18х2+12х+2
Вынесем общий множитель за скобку
2(9х2+6х+1)
2) Применим формулу квадрата суммы
2(3х+1)2

18.

РАЗЛОЖИТЕ МНОГОЧЛЕН НА
МНОЖИТЕЛИ
18х2+12х+2
Вынесем общий множитель за скобку
2(9х2+6х+1)
2) Применим формулу квадрата суммы
2(3х+1)2
18х2+12х+2=2(9х2+6х+1)=2(3х+1)2=
=2(3х+1)(3х +1)

19.

РАЗЛОЖИТЕ МНОГОЧЛЕН НА
МНОЖИТЕЛИ:
9с2-6ху+у2+12х-4у
Какие
способы разложения многочлена
на множители нужно использовать?

20.

РАЗЛОЖИТЕ МНОГОЧЛЕН НА
МНОЖИТЕЛИ:
9с2-6ху+у2+12х-4у
Какие
способы разложения многочлена
на множители нужно использовать?
Способ группировки
(9х2-6ху+у2)+(12х-4у)= (3х-у)2+4(3х-у)=
=(3х-у)(3х-у+4)

21.

РАЗЛОЖИТЕ МНОГОЧЛЕН НА
МНОЖИТЕЛИ:
4-а2-2а(4-а2)+а2(4-а2)=

22.

РАЗЛОЖИТЕ МНОГОЧЛЕН НА
МНОЖИТЕЛИ:
4-а2-2а(4-а2)+а2(4-а2)=
=1(4-а2)-2а(4-а2)+а2(4-а2) =

23.

РАЗЛОЖИТЕ МНОГОЧЛЕН НА
МНОЖИТЕЛИ:
4-а2-2а(4-а2)+а2(4-а2)=
=1(4-а2)-2а(4-а2)+а2(4-а2) =
=(4-а2)(1-2а+а2)=( 22-а2)(1-а)2 =

24.

РАЗЛОЖИТЕ МНОГОЧЛЕН НА
МНОЖИТЕЛИ:
4-а2-2а(4-а2)+а2(4-а2)=
=1(4-а2)-2а(4-а2)+а2(4-а2) =
=(4-а2)(1-2а+а2)=( 22-а2)(1-а)2 =
=(2 - а)(2 + а) )(1-а)2

25.

ДЛЯ УПРОЩЕНИЯ ВЫРАЖЕНИЙ И
ВЫЧИСЛЕНИЙ МОЖНО ИСПОЛЬЗОВАТЬ
1)Вынесение общего множителя за скобку;
2) Формулы квадрата суммы, квадрата
разности, разности квадратов;
3) Способ группировки;
4) Одновременно два или три способа
разложения.

26.

ДОМАШНЕЕ ЗАДАНИЕ
§ 19, № 708, № 710, № 712.