Similar presentations:
Применение нескольких способов разложения многочленов на множители
1.
7 А класс2.
Три пути ведут к познанию:путь размышления –
это путь самый благородный,
путь подражания –
это путь самый легкий
и путь опыта –
это путь самый горький.
Конфуций
3. Убедимся в том, что разложение на множители –действие полезное.
Убедимся в том, что разложение на множители –действие полезное.
1.Решить уравнение 2х2+х –6 =0. Воспользуемся разложением многочлена
на множители: х2-6х +5= х2-х-5х+5= (х2-х)+(-5х+5)=х(х-1)-5(х-1)=(х-1)(х-5),
х-1=0 или х-5=0
х1 = 1 , х2 = 5.
2. Найти значение числового выражения 532-472.
612-392
Самое эффективное решение – дважды воспользоваться формулой
разности квадратов:
532-472 = (53-47)(53+47) = 6•100 = 6 = 3
612-392 (61-39)(61+39) 22•100 22 11
Разложение на множители позволило сократить дробь. Позднее мы
оценим это и при выполнении действий с алгебраическими дробями.
3. Доказать, что для любого n N выражение n3+3n2+2n делится без
остатка на 6.
4. Соединить линиями соответствующие части определения.
Представлениемногочлена в виде
суммы двух или
нескольких многочленов.
Разложение
многочлена
на множители - это
Представление
многочлена в виде
произведения двух или
нескольких одночленов.
Представление
многочлена в виде
произведения двух или
нескольких многочленов.
5.
Способы разложения многочленана множители:
вынесение
общего
множителя за скобки
способ группировки
формулы
сокращенного
умножения
6. Восстановить порядок выполнения действий при разложении многочлена на множители способом группировки.
1Чтобы
разложить
многочлен на
множители
способом
группировки,
нужно
2
вынести
в каждой группе общий
множитель в виде
многочлена за скобки
группировать его члены
так, чтобы слагаемые
в каждой группе имели
общий множитель
3
вынести
в каждой группе общий
множитель в виде
одночлена за скобки
7. Отметить верные выражения
a)b)
c)
d)
e)
a2 + b2 - 2ab = (a-b)2
m2 + 2mn - n2 = (m-n)2
2pt – p2 – t2 = (p-t)2
(3a-5)(3a+5)=9a2 – 25
(a5-b5)(a5+b5)=a25-b25
8. Дополнить выражение одночленом так, чтобы полученный трехчлен можно было представить в виде квадрата суммы или квадрата
разности:a2+12a + …
4x2 - … + 25y2
m2 + 5m + …
b4 – 6b2c + …
1/4x4 + … + y6
m12 + n6 + …
36
20xy
25/4
9c2
x2y3
2m6n3
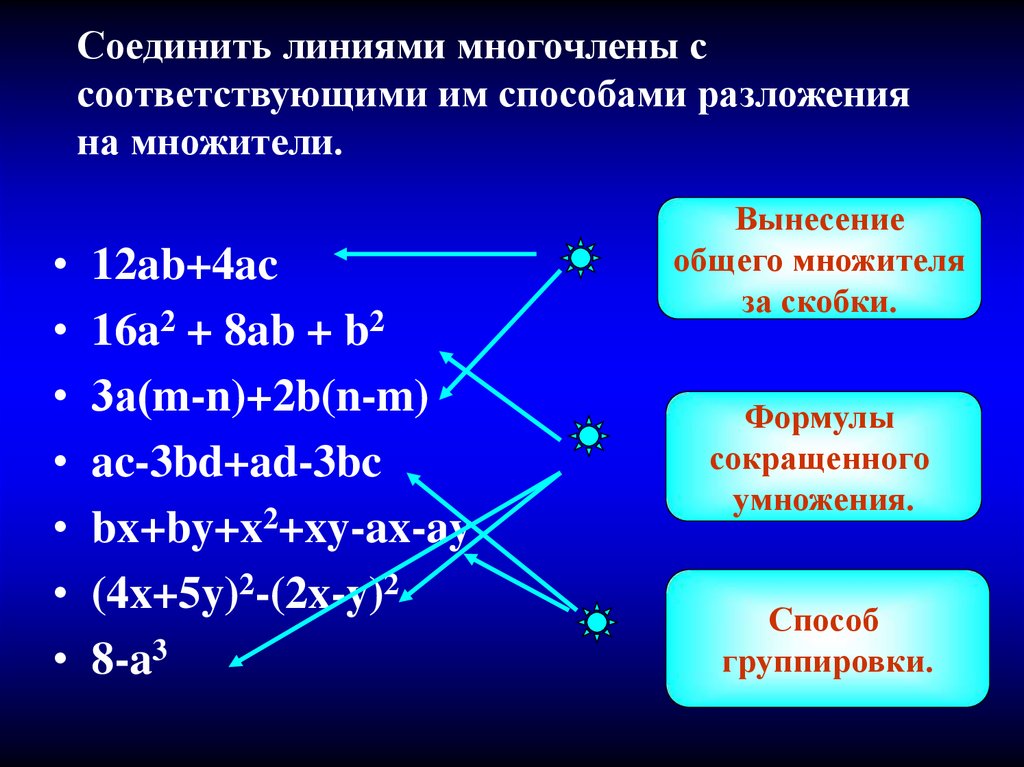
9. Соединить линиями многочлены с соответствующими им способами разложения на множители.
12ab+4ac
16a2 + 8ab + b2
3а(m-n)+2b(n-m)
ac-3bd+ad-3bc
bx+by+x2+xy-ax-ay
(4x+5y)2-(2x-y)2
8-a3
Вынесение
общего множителя
за скобки.
Формулы
сокращенного
умножения.
Способ
группировки.
10. При разложении многочлена на множители полезно соблюдать следующий порядок:
12
3
• вынести общий множитель за
скобки (если он есть);
• попробовать разложить многочлен
на множители по формулам
сокращенного умножения;
• попытаться применить способ
группировки (если предыдущие
способы не привели к цели).
11.
Разложение намножители
Пояснения
12a3 – 3a = 3a(4a2 – 1)= Выношу общий
множитель 3а за
= 3a(2a-1)(2a+1)
скобки.
Раскладываю
(4а2-1) на множители
по формуле разности
квадратов.
12. Завершить разложение на множители:
1.7а2 – 28=7(а2 – 4)=2.- 2b2 + 18= -2(b2 - 9)=
3.3а2 + 6а + 3= 3(а2 +2а +1)=
4.- х2 +4х - 4= - (х2 - 4х +4)=
5.с2 - b2 + 8с +8b =(с2 - b2) +
+(8с+8b)=(с – b)(с + b) +8(с + b)=
1. 7(а – 2)(а +2)
2. - 2(b – 3)(b + 3)
3. 3(а +1)2
4. - (х – 2)2
5. (с + b)(с – b + 8)
Найти числовое значение выражения
а2 + b2 + 2ab + 17, если a + b = 4.
33
13. Разложить на множители:
1.2.
3.
4.
5.
6.
ах2 – ау2
у 6 – у4
4а2b – 8аb +4b
- 10х2 +40ах – 40а2
х2 – 2ху +у2 – 6х +6у
4а2 +4аb + b2 +12а +6b
1.
2.
3.
4.
5.
6.
а(х – у)(х +у)
(у3 – у2)(у3 + у2)
4b(а – 1)2
- 10(х – 2а)2
(х – у)(х – у – 6)
(2а + b) (2а + b +6)
1. Вынести общий множитель за скобки
(если он есть).
2. Попробовать разложить многочлен на
множители по формулам сокращенного
умножения.
3. Применить способ группировки (если
предыдущие способы не привели к цели).
14. Проверь себя
Разложите на множители, используя различные способы:• 5а3 – 125аb2
5а(а - 5b)(а + 5b) 5а(а2 - 25 b2)
5а(а - 5b)2
• 63аb3 – 7а2b
7а2b2(9b – 1)
аb(63 b2 – 7а)
7аb(9b2 – а)
• 3а2 + 6а + 3
3(а +1)(а – 1)
3(а + 1)2
(3а + 1)2
• а2 - b2 + 6а +6b
(а + b)(а – b + 6)
( а – b)2 (а2 - b2) + (6а + 6b)
• 6х2 – 12х + 6
(3х – 3)2
6(х – 1)2
(х – 1)(х + 6)
15.
Молодец!16.
Попробуйеще раз!















 mathematics
mathematics








