Задачи линейного программирования и их решение в современных вычислительных средах. Лекция №12. Продолжение

1.

Задачи линейного
программирования и их решение в
современных вычислительных
средах
Лекция №12. Продолжение

2.

Инструменты решения задач ЛП
Excel: Поиск
решения
Matlab: функция
linprog
Mathcad: блок
Given и функции
нахождения
оптимума

3.

Решение задачи ЛП в средах Matlab и
Mathcad
Для решения задачи ЛП в средах Matlab и
Mathcad целевую функцию и ограничения
удобнее записать в матричном виде.
Далее мы рассмотрим запись в матричном
виде для двух типов задач ЛП.

4.

Целевая функция задачи ЛП
C=С(x1, x2, …, xn)=c1x1+c2x2+….+cnxn
n
Или:
С cjxj
j 1
:
.
n – число переменных модели.
ЦФ в векторном виде:
C=C(x)=cт x,
где т – транспонирование,
- матричное произведение.
Или:
C= C(x)= c x,
где - скалярное
произведение векторов
с1
x1
с2
x2
с , x .
...
...
с
x
n
n

5.

Пример 1. Стандартная (нормальная)
форма задачи ЛП
1. ЦФ => максимум.
Ограничения–линейные неравенства (≤) + условие
положительности всех переменных:
a1,1 x1 a1, 2 x2 ... a1, n xn b1
...
am ,1 x1 am , 2 x2 ... am , n xn bm
x j 0, j 1,2,..., n
Или в сокращенной записи:
n
ai , j x j bi
,
j 1
x j 0
i=1, 2, …, m,
J=1, 2, …, n.

6.

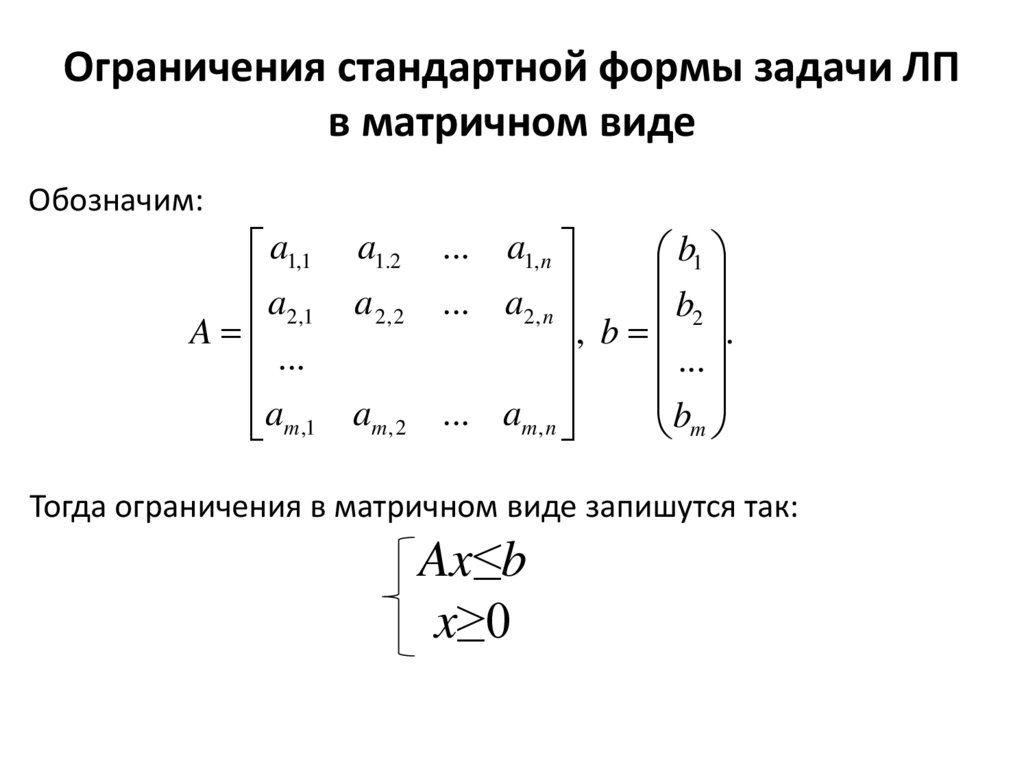
Ограничения стандартной формы задачи ЛП
в матричном виде
Обозначим:
a1,1 a1.2 ... a1, n
b1
a
a 2, 2 ... a2, n
b2
2 ,1
A
, b .
...
...
b
a
a
...
a
m,2
m, n
m
m ,1
Тогда ограничения в матричном виде запишутся так:
Ax≤b
x≥0

7.

Пример 2. Транспортная задача
На n станциях отправления A1, …, An имеется,
соответственно, a1, …, an единиц некоторого груза. Этот груз
следует доставить в m пунктов назначения B1, …, Bm, и в
каждый из них должно быть завезено, соответственно, b1, …,
bm единиц этого груза. Стоимость перевозки одной единицы
груза из пункта Ai в пункт Bk равна ci,k. Составить такой
план перевозок, чтобы суммарная стоимость перевозок была
минимальной.
Считать, что количество всего груза на двух пунктах
отправления равно потребности в грузе на всех трех пунктах
назначения, то есть:
a1 + … + an = b1 + … + bm.

8.

Пример 2. Транспортная задача
Расположим исходные данные этой задачи в виде таблицы:
Пункт
Пункт назначения Запас груза
отправления B
… Bm
1
A1
с1,1
… с1, m
a1
…
…
…
…
…
An
сn,1
… сn,m
an
Потребность b1
… bm
в грузе

9.

Пример 2. Транспортная задача
Обозначим: xi,k – количество перевезенного груза из пункта
Ai в пункт Bk . Тогда ЦФ (которую нужно минимизировать)
равна:
2
3
C ci , k xi , k
i 1 k 1
Ограничения:
3
x
k 1
i,k
2
x
i 1
i,k
ai , i 1,2
bk , k 1,2,3
xi , k 0, i 1,2; k 1,2,3

10.

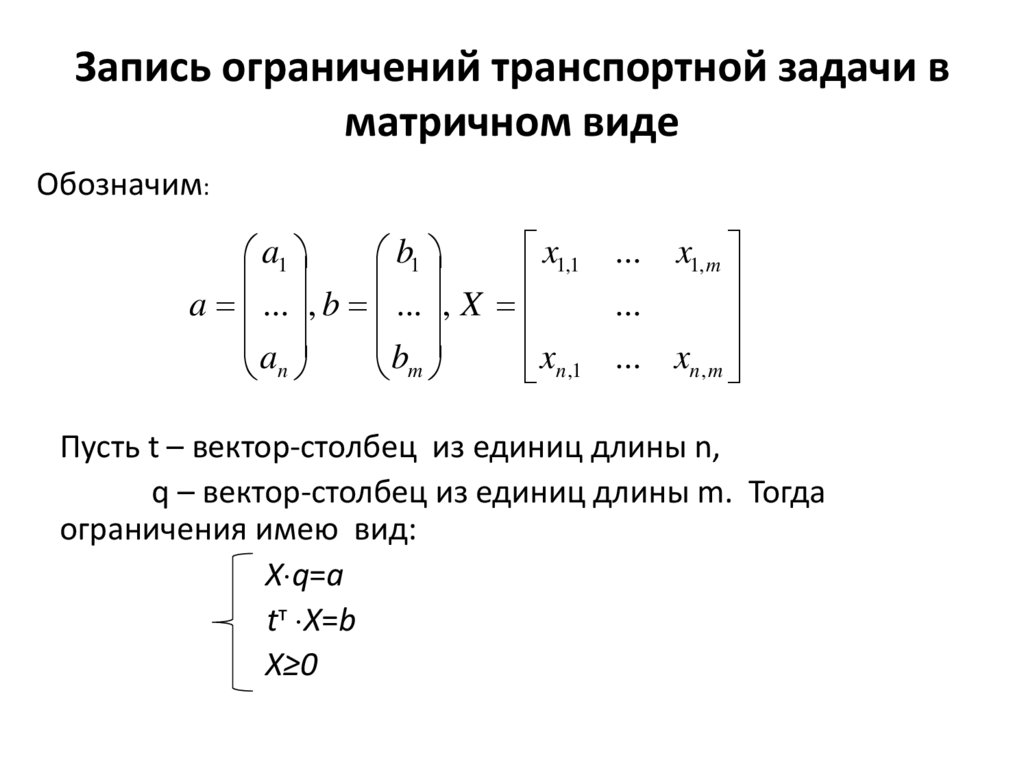
Запись ограничений транспортной задачи в
матричном виде
Обозначим:
x1,1 ... x1, m
a1
b1
a ... , b ... , X
...
a
b
xn ,1 ... xn , m
n
m
Пусть t – вектор-столбец из единиц длины n,
q – вектор-столбец из единиц длины m. Тогда
ограничения имею вид:
X q=a
tт X=b
X≥0

11.

Решение задачи ЛП (на примере стандартной
формы) в среде Mathcad
• Задание параметров задачи – присваиванием или вводом:
a1,1 a1.2 ... a1, n
b1
a
a 2, 2 ... a2, n
b2
2 ,1
A :
, b : .
...
...
b
a
a
...
a
m,2
m, n
m
m ,1
• Задание начального приближения: x:=0.
• Запись ЦФ: C(x):= c x
• Given
Ограничения: Ax≤b
x≥0
• Result:=Maximize(C,x) оптимальное решение задачи ЛП
См. https://gigabaza.ru/doc/80570.html и ЛР11.

12.

Ограничение целочисленности х в среде Mathcad
Для некоторых версий MathCAD существует пакет расширения SOEP
(Solving and Optimization Extension Pack), в котором имеется
возможность уточнить тип результата - просто в завершающих
функциях блока Given последним параметром ставится строка,
указывающая тип переменной в системе уравнений. Местоположение
целой переменной обозначается
I, бинарной - В, и т.д.:
f(x1,x2)=5*x2-3*x1
Given
2x1+3x2≤5 x1≥0 x2≥0
Minimize (f,x1,x2,"II")
В базовой комплектации MathCAD нет инструментов для установления
целочисленных ограничений.
НО можно самостоятельно разработать такой алгоритм!
См., например, http://blog.kislenko.net/show.php?id=974

13.

Решение задачи ЛП в среде Matlab – функция
linprog
x = linprog(C,A,b) решает min cт x таким образом,
что A x ≤ b.
x = linprog(C,A,b,Aeq,beq) включает ограничения
равенства Aeq x = beq. Установите A = [] и b = [] если
никакие неравенства не существуют.
x = linprog(f,A,b,Aeq,beq,lb,ub) задает набор нижних
и верхних границ на переменных проекта, x, так, чтобы
решением всегда был в области значений lb ≤ x ≤ ub.
Установите Aeq = [] и beq = [] если никакие равенства
не существуют.
Функция linprog принадлежит пакету Optimization Toolbox,
который требует дополнительной установки.