Similar presentations:
Задачи линейного программирования
1.
Задачи линейногопрограммирования
2.
Линейное программированиеЛинейное программирование – это область
математики, в которой изучаются методы
исследования
и
отыскания
экстремальных
значений некоторой линейной функции, на
аргументы
которой
наложены
линейные
ограничения.
Такая линейная функция называется целевой, а
набор
количественных
соотношений
между
переменными,
выражающих
определенные
требования экономической задачи в виде
уравнений или неравенств, называется системой
ограничений.
Слово программирование введено в связи с тем, что
неизвестные переменные обычно определяют
программу или план работы некоторого субъекта.
3.
Математическая модель задачи оптимизации ЗЛП этосовокупность
соотношений,
содержащих
целевую
функцию и ограничения на ее аргументы записывается в
общем виде так:
F ( x) c1x1 c2 x2 ... c j x j ... cn xn m a x(min)
при ограничениях
a11 x1 a12 x2 ... a1 j x j ... a1n xn b1 ,
a12 x2 a22 x2 ... a2 j x j ... a2 n xn b2 ,
...............................................................,
.
ai1 x1 ai 2 x2 ... aij x j ... ain xn bi ,
..............................................................,
am1 x1 am 2 x2 ... amj x j ... amn xn bm
x j 0, i 1, m, j 1, n.
x j - неизвестные,
aij , bi , c j - заданные постоянные величины
Ограничения могут быть заданы уравнениями.
4.
В краткой записи ЗЛП имеет вид:n
F ( x) c j x j max(min)
j 1
n
a x b ,
j 1
ij
j
i
при ограничениях
x j 0, i 1, m, j 1, n.
Экстремум целевой функции ищется на допустимом
множестве решений, определяемом системой ограничений,
причем все или некоторые неравенства
в системе
ограничений могут быть записаны в виде уравнений.
5.
Для составления математической моделиЗЛП необходимо :
1. обозначить переменные;
2. составить целевую функцию;
3. записать систему ограничений в соответствии с
целью задачи;
4. записать систему ограничений с учетом
имеющихся в условии задачи показателей.
Если все ограничения задачи заданы
уравнениями, то модель такого вида
называется канонической.
Если хоть одно из ограничений дано
неравенством, то модель неканоническая.
6.
7.
8.
Пример.Записать в форме основной задачи ЛП задачу: найти
максимум функции
F 3x1 2 x2 5x4 x5
при условиях
2 x1 x3 x4 x5 2,
x x 2 x x 3,
1 3
4
5
2 x2 x3 x4 2 x5 6,
x1
x4 5 x5 8,
x1 , x2 , x3 , x4 , x5 0.
9.
Геометрическое решение задачлинейного программирования






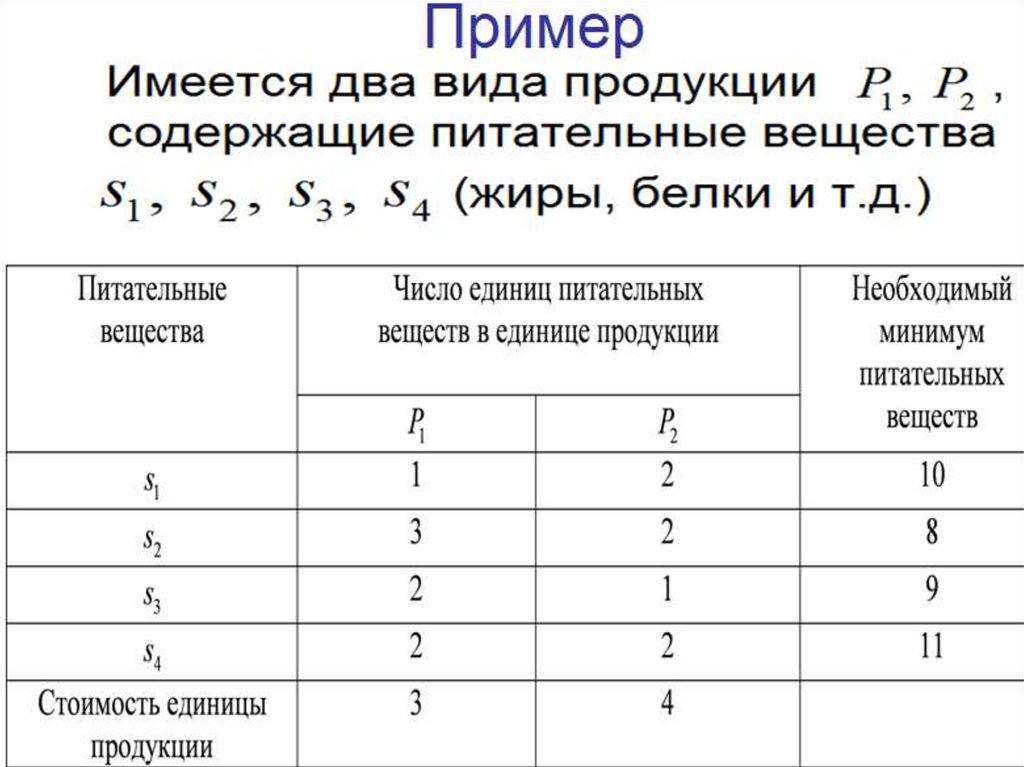



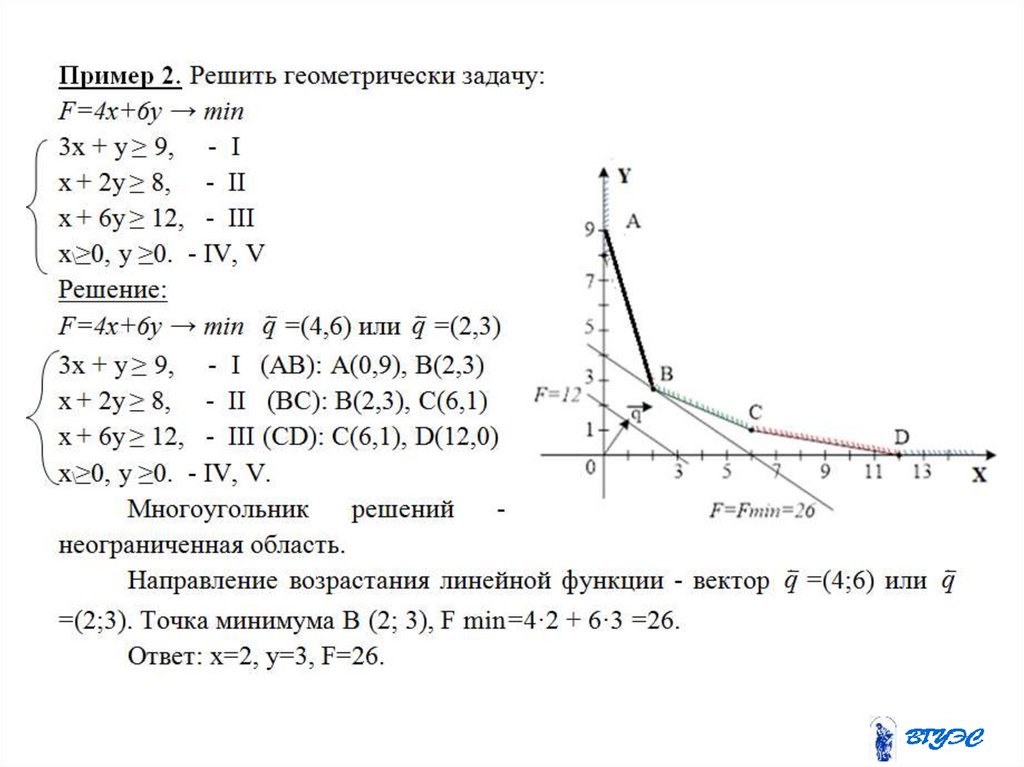
 mathematics
mathematics








