Линейное программирование. Задачи

1. ИСПОЛЬЗОВАНИЕ ПАКЕТА Microsoft EXCEL ПРИ ОБРАБОТКЕ РЕЗУЛЬТАТОВ, ПОЛУЧЕННЫХ В ХОДЕ ВЫПОЛНЕНИЯ ИССЛЕДОВАТЕЛЬСКОЙ РАБОТЫ

2. Этапы принятия решения

Сбор информации о состоянии
объекта
Определение цели управления
(критерия оптимальности)
Выработка решения
Выдача управляющей информации
2

3. Общая задача оптимизации

3

4. Общая задача оптимизации

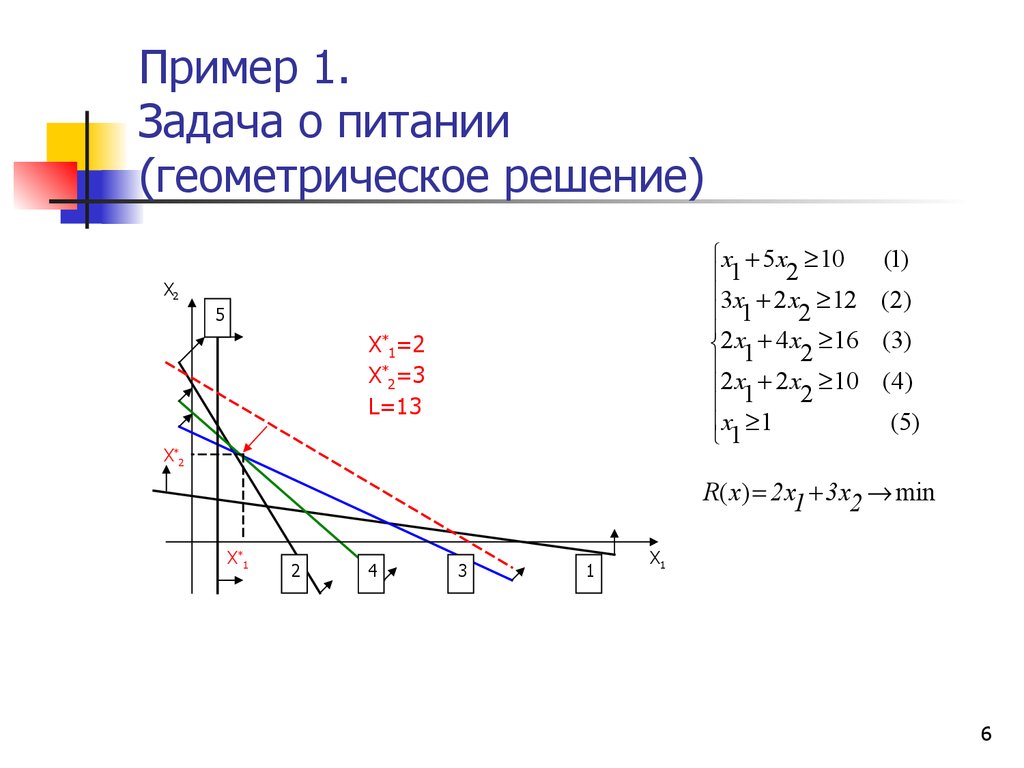
4

5. Пример 1. Задача о питании

5

6. Пример 1. Задача о питании (геометрическое решение)

x 5 x 10
2
1
3x 2 x 12
1
2
2 x1 4 x2 16
2 x 2 x 10
2
1
x 1
1
X2
5
X*1=2
X*2=3
L=13
X*2
(1)
(2)
(3)
(4)
(5)
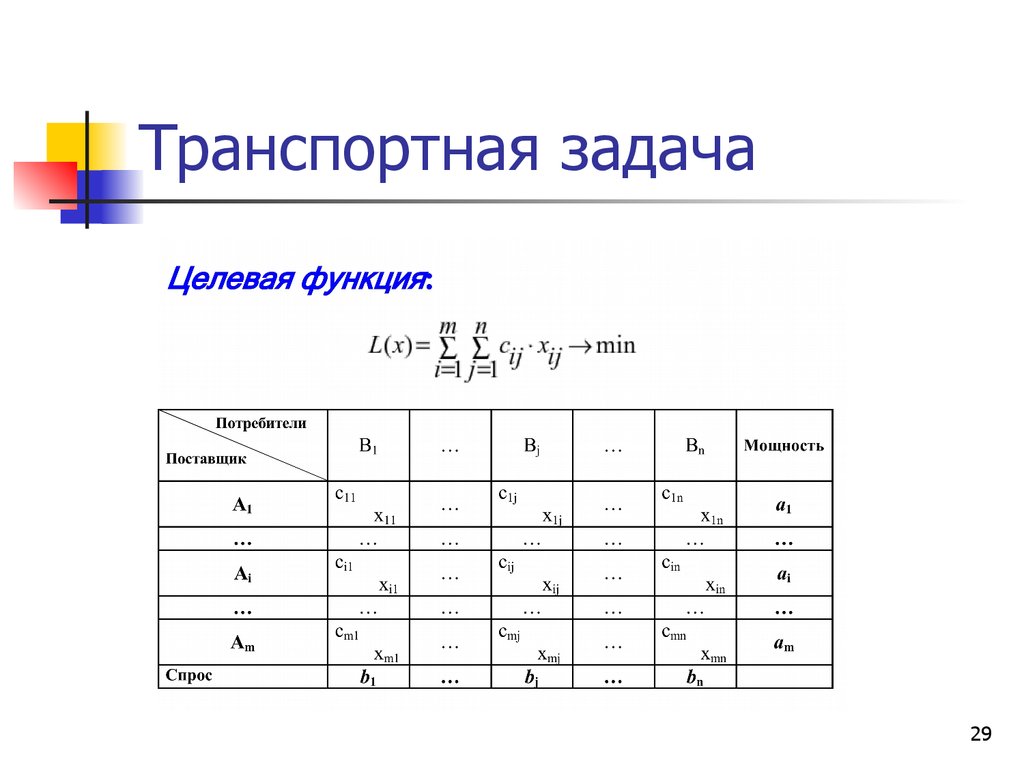
R( x) 2 x1 3 x2 min
X*1
2
4
3
1
X1
6

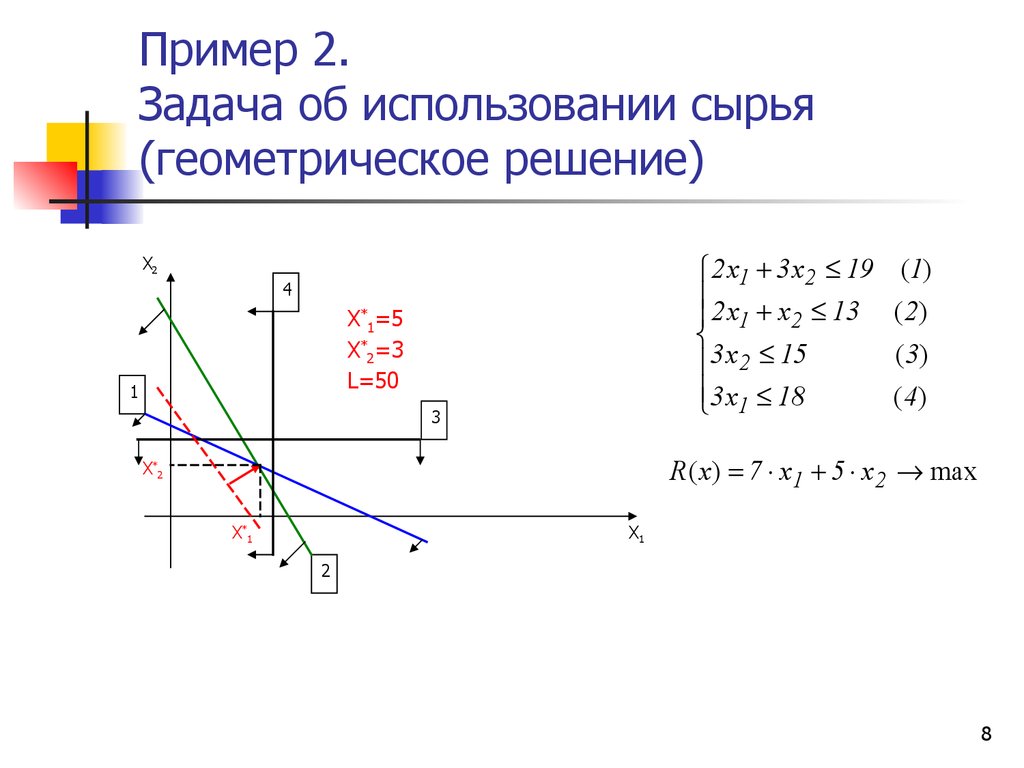
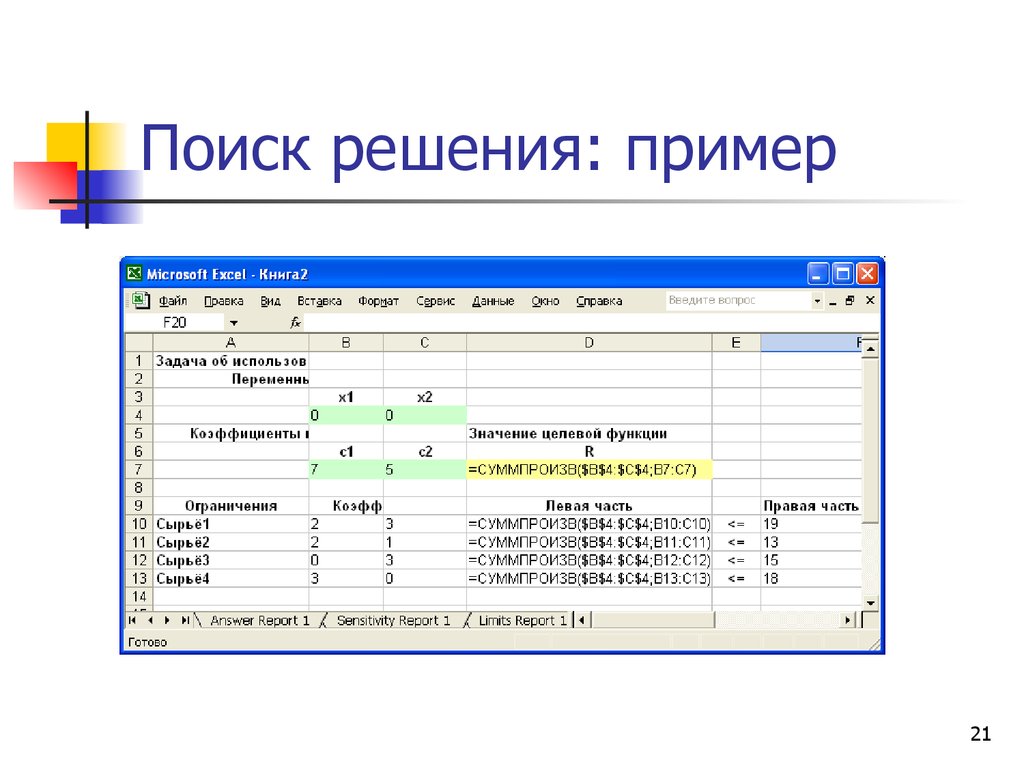
7. Пример 2. Задача об использовании сырья

7

8. Пример 2. Задача об использовании сырья (геометрическое решение)

2 x1 3 x2 19
2 x x 13
1 2
3 x2 15
3 x1 18
X2
4
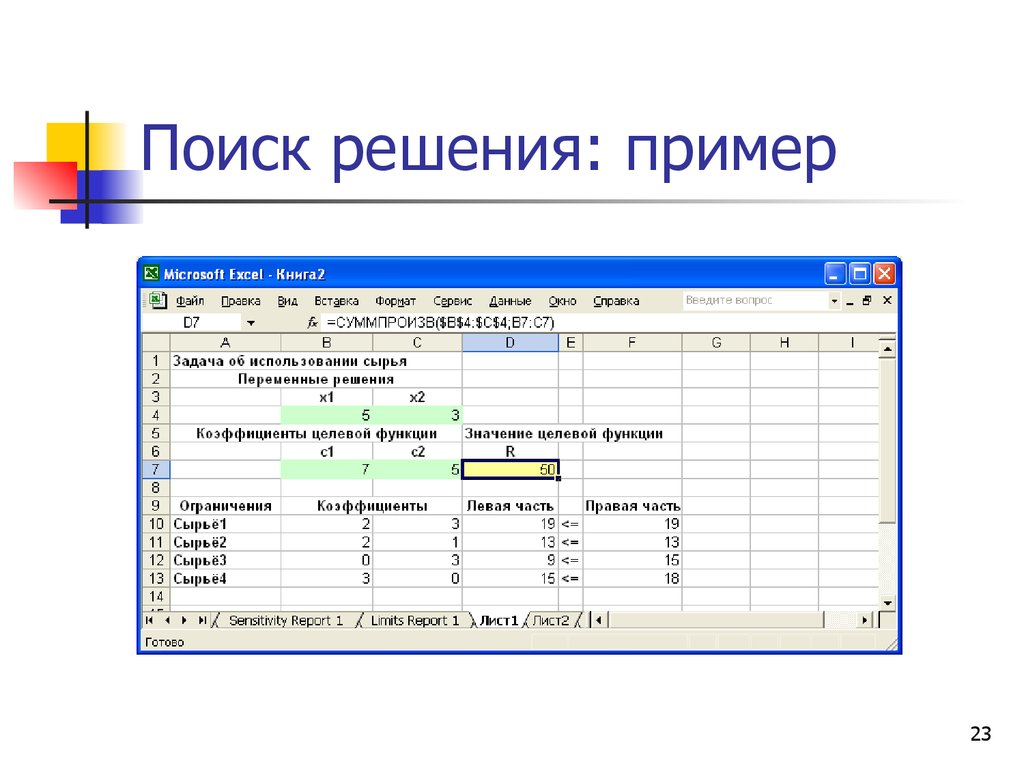
X*1=5
X*2=3
L=50
1
3
(1)
( 2)
( 3)
(4 )
R( x) 7 x1 5 x 2 max
X*2
X*1
X1
2
8

9. Симплекс-метод: шаг 1

Целевая
функция
R 7 x1 5 x2 max
Система ограничений
2 x1 3 x2 19
2 x x 13
1
2
3 x 2 15
3 x1 18
Условие
x1 , x 2 0
Целевая функция
R1 7 x1 5 x 2 min
Система ограничений
2 x1 3 x 2 x3 19
2 x x x 13
1
2
4
3 x 2 x5 15
3 x1 x6 18
Условие
x1 , x 2 , x3 , x4 , x5 , x6 0
9

10. Симплекс-метод: шаг 2

1-е базисное решение: свободные неизвестные
x3
x
4
x5
x6
x1 , x 2
19 2 x1 3 x 2
13 2 x1 x 2
15 3 x 2
R1 7 x1 5 x2
18 3 x1
x1 0, x 2 0, x3 19, x4 13, x5 15, x6 18
R1 7 x1 5 x 2 0
10

11. Симплекс-метод: шаг 2

Преобразование системы ограничений:
x2 переводится в базис, x5 - в свободные
x2
x
3
x4
x
6
1
5 x5
3
1
19 2 x1 3 5 x5 4 2 x1 x5
3
1
1
13 2 x1 5 x5 8 2 x1 x5
3
3
18 3 x1
1
5
R1 7 x1 5 5 x5 25 7 x1 x5
3
3
11

12. Симплекс-метод: шаг 2

2- е базисное решение: свободные неизвестные
x2
x3
x
4
x
6
1
5 x5
3
4 2 x1 x5
1
8 2 x1 x5
3
18 3 x1
x1 , x5
5
R1 25 7 x1 x5
3
x1 0, x 2 5, x3 19, x4 13, x5 0, x6 18
5
R1 25 7 x1 x5 25
3
12

13. Симплекс-метод: шаг 2

3 - е базисное решение: свободные неизвестные
1
1
x1 2 2 x3 2 x5
x 5 1 x
5
7
11
2
3
R
39
x
x5
1
3
2
6
2
x 4 x x
3
5
4
3
3
3
x6 12 x3 x5
2
2
x3 , x5
x1 2, x 2 5, x3 0, x4 4, x5 5, x6 12
R1 39
13

14. Симплекс-метод: шаг 2

4 - е базисное решение: свободные неизвестные
x1
x
2
x
5
x6
1
3
5 x3 x4
4
4
1
1
3 x3 x4
2
2
3
3
6 x3 x4
2
2
3
9
3 x3 x4
4
4
x3 , x4
3
11
R1 50 x3 x4
4
4
14

15. Симплекс-метод: шаг 2

4 - е базисное решение (оптимальное)
x1 5, x 2 3, x3 0, x4 0, x5 6 , x6 3
3
11
R1 50 x3 x4 50
4
4
Коэффициенты при
x3 , x4 положительны
15

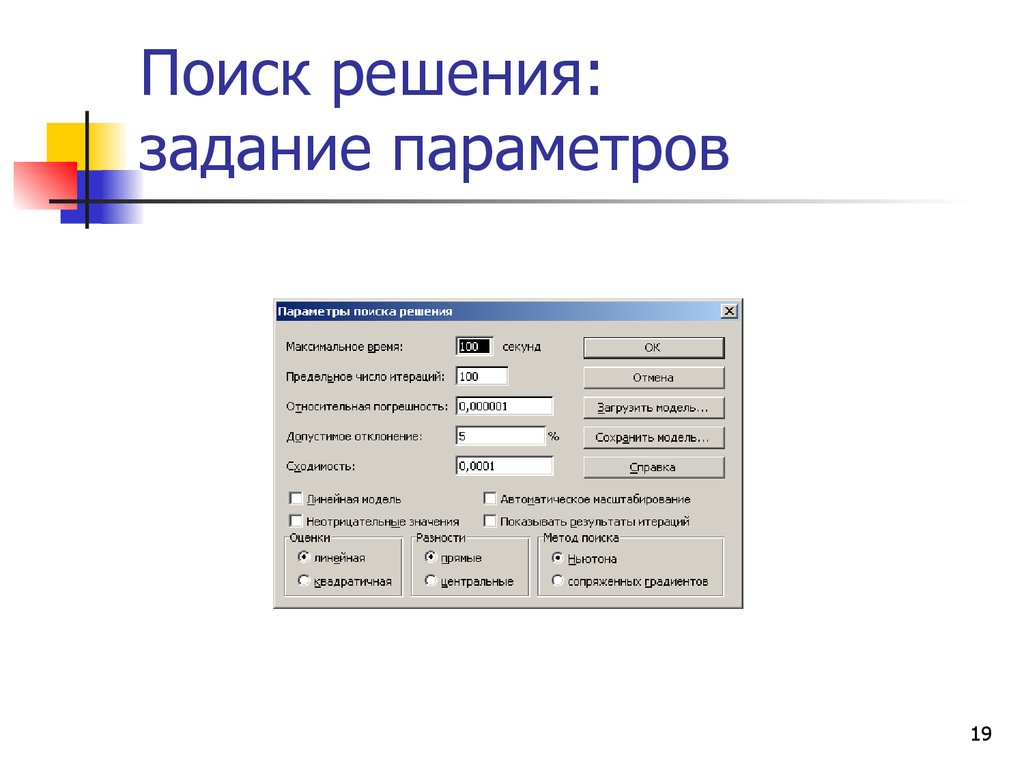
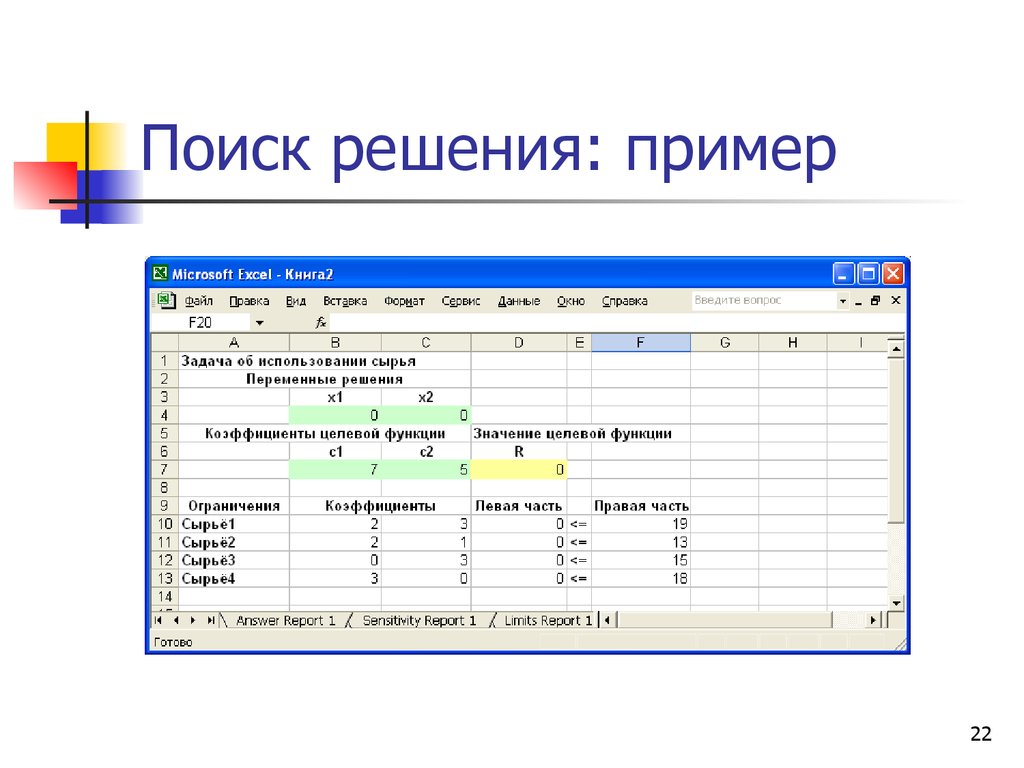
16. Поиск решения: этапы

Подготовить рабочий лист
Выполнить команду СЕРВИС-Поиск
решения (Данные-Поиск решения)
Установить целевую ячейку
Задать изменяемые ячейки
Добавить ограничения
Установить параметры
Выполнить
16

17. Поиск решения: установка целевой ячейки, изменяемых ячеек и ограничений

Диапазон, в котором
располагаются
неизвестные
величины, влияющие
на целевую функцию
Ссылка на ячейку с
целевой функцией
Список
ограничений
17

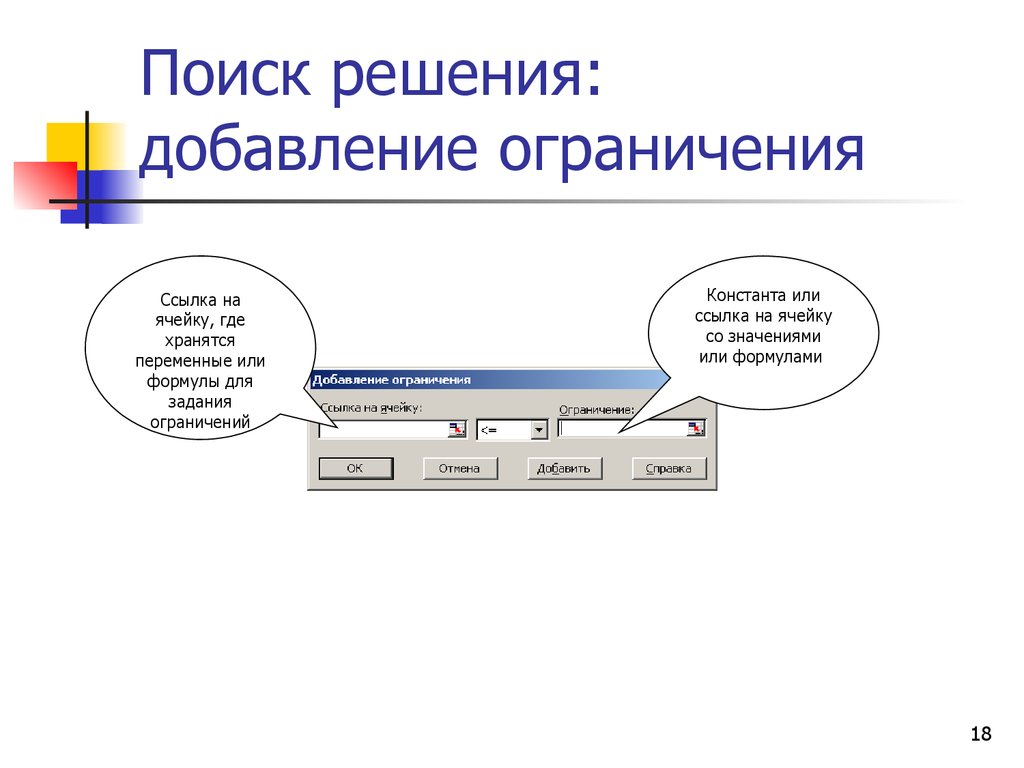
18. Поиск решения: добавление ограничения

Ссылка на
ячейку, где
хранятся
переменные или
формулы для
задания
ограничений
Константа или
ссылка на ячейку
со значениями
или формулами
18

19. Поиск решения: задание параметров

19

20. Поиск решения: подготовка рабочего листа

20

21. Поиск решения: пример

21

22. Поиск решения: пример

22

23. Поиск решения: пример

23

24. Задача ассортиментной оптимизации

24

25. Задача ассортиментной оптимизации

25

26. Задача рецептурной оптимизации

26

27. Задача рецептурной оптимизации

27

28. Транспортная задача

28

29. Транспортная задача

29

30. Транспортная задача

30