Числовая окружность. Формулы

1.

2.

Окружность
P
М
N
A
О
А
O
C
D

3.

Деление на части
1)на 2 части
2)на 4 части
С
3)на 8 частей
С
R
В
А
В
А
K
В
A
AА
M
D
4)на 12 частей
С
O
D
5)на 6 частей
Z
P
O
Z
F
B
A
G
B
A
T
E
H
D
E
N
H

4.

Градусы и радианы
1 рад ≈ 57°
π ≈ 3,14
π(рад) =180°
R
π
0

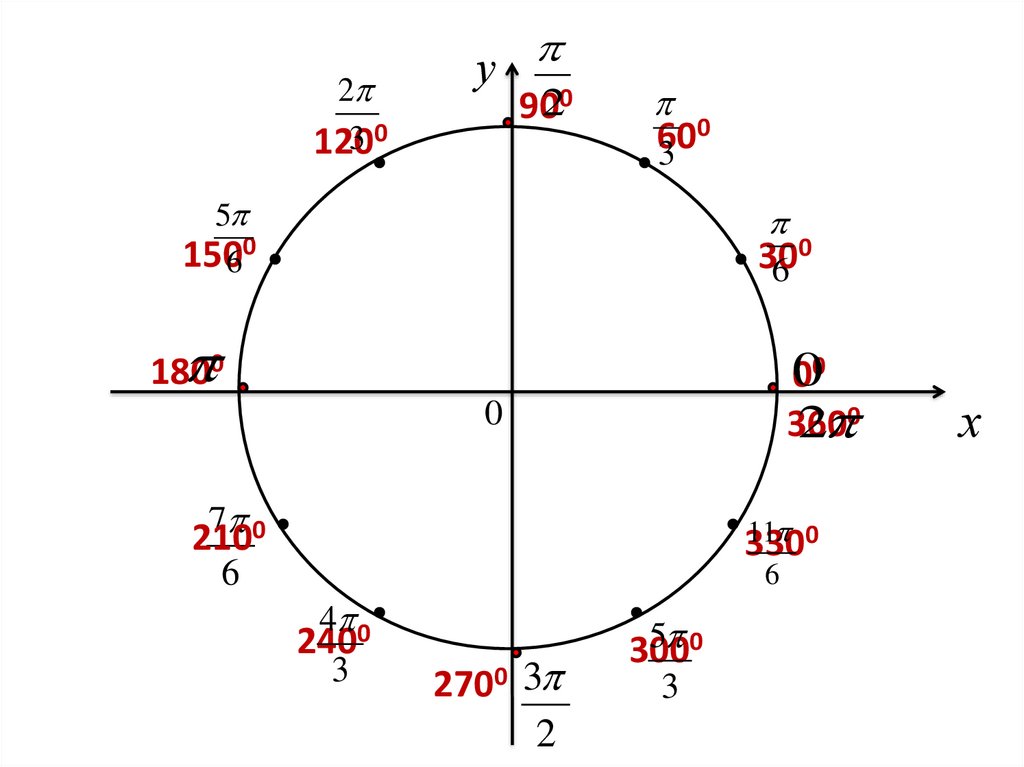
5.

2
30
120
у
9020
0
60
3
5
15060
0
30
6
0
180
0
00
360
2 0
0
7 0
210
6
11 0
330
6
4 0
240
3
2700 3
2
5 0
300
3
х

6.

у
9020
3 0
135
4
0
45
4
0
180
0
00
360
2 0
0
7 0
315
5 0
225
4
4
2700 3
2
х

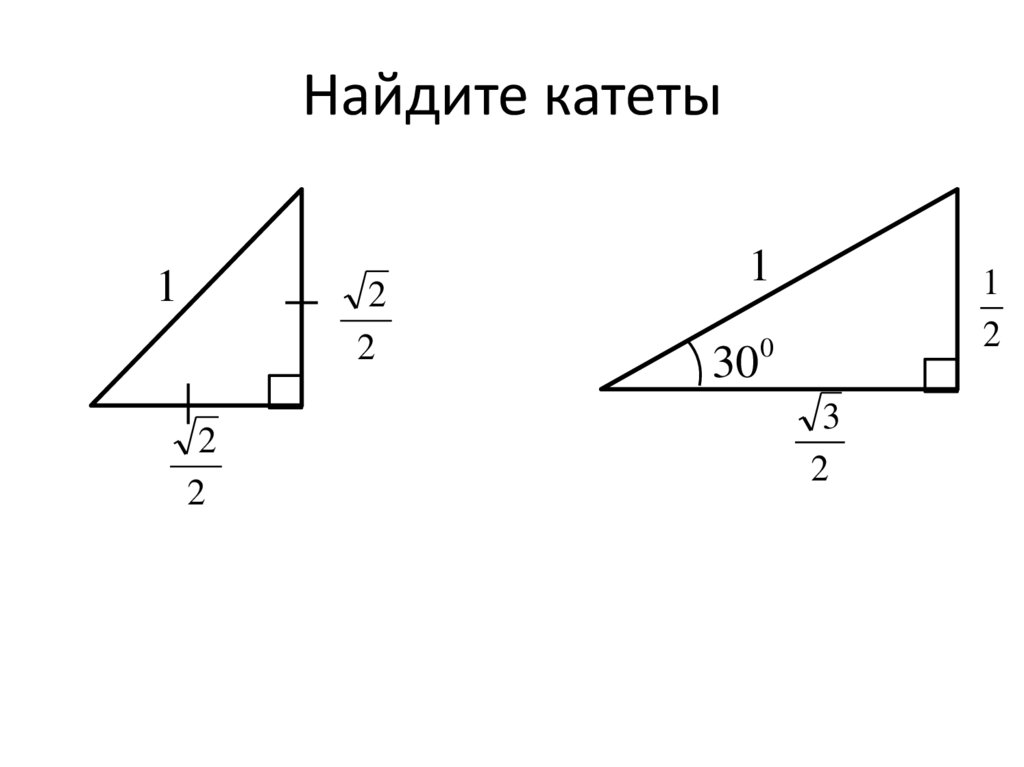
7.

Найдите катеты
1
2
2
2
2
1
30
1
2
0
3
2

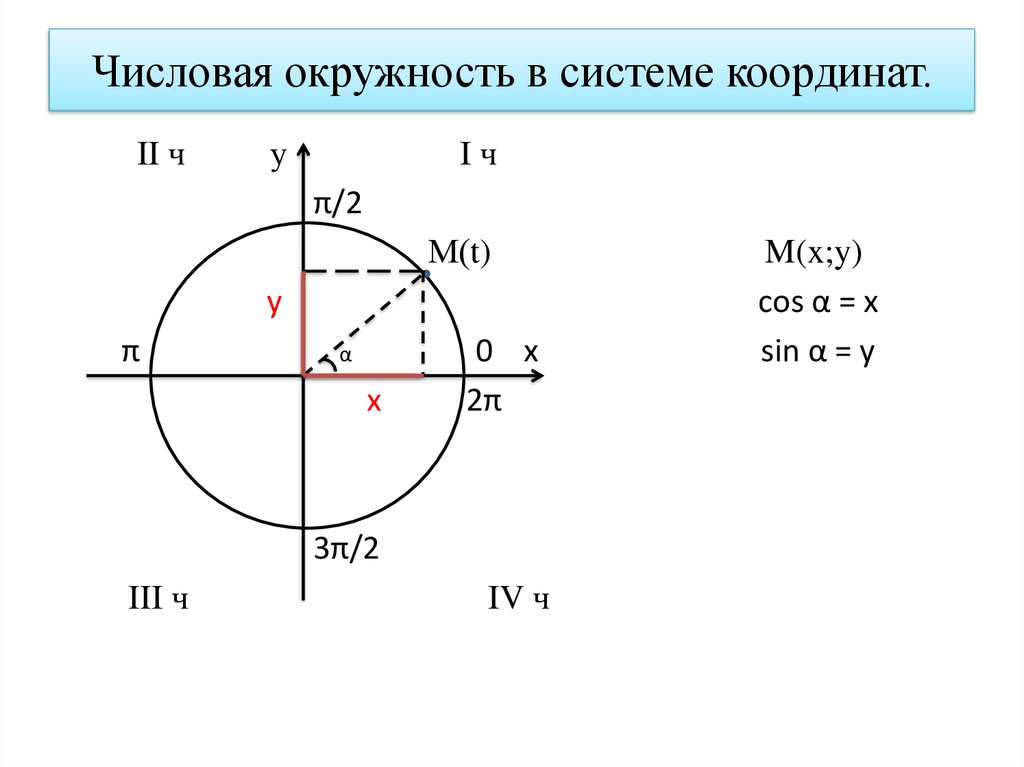
8.

Числовая окружность в системе координат.
II ч
у
Iч
π/2
М(t)
у
π
α
х
0 х
2π
3π/2
III ч
IV ч
M(x;y)
cos α = x
sin α = y

9.

Координаты и углы
у
3
135°
90°
2
1
2
120°3
3
2
4
2
2
5
150°
6
180°
360°
45°
4
30°
6
1
2
1 0
0°
-1
1
3 2
2
2
2
7
210°
6
5
225°
4
4
240°
3
1
2
0
2
2
0
360
2
3
2
1
2
11
330°
2
2
3
2 -1
270° 3
2
7
4
315°
5300°
3
6
х

10.

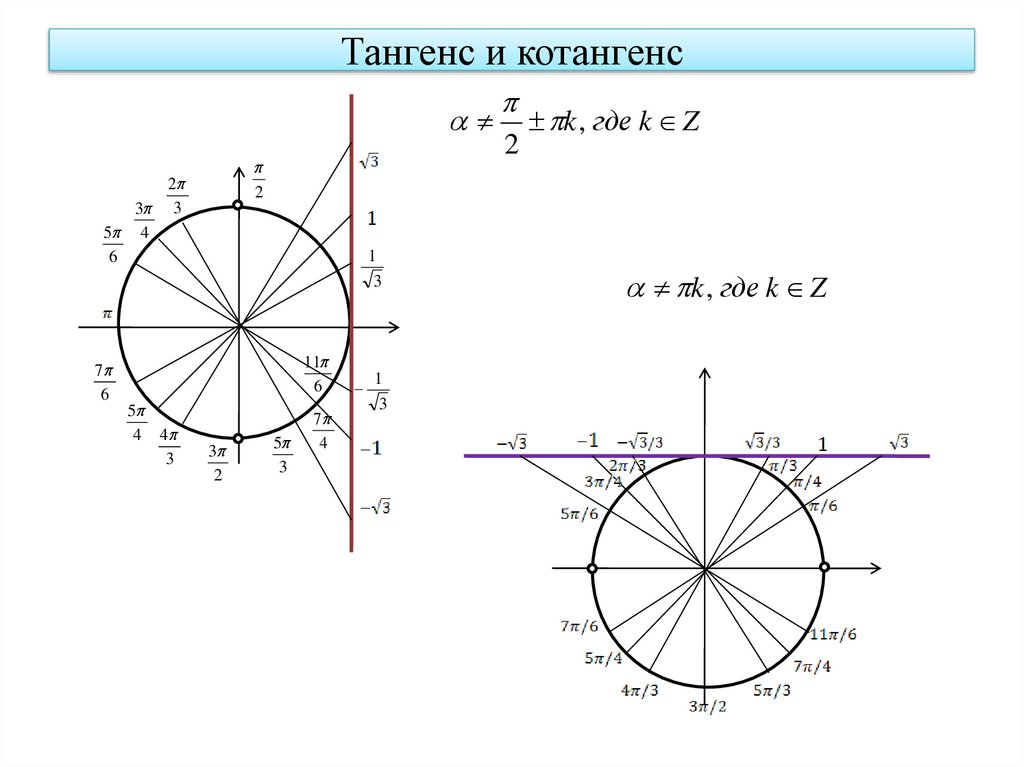
11.

Тангенс и котангенс
2
2
3 3
5 4
6
7
6
1
3
11
6
5
4 4
3
3
2
5
3
7
4
1
3
2
k , где k Z
k , где k Z

12.

Устная работа
то
точка
Координаты
Р1
2 2
;
2 2
Р2
1 3
;
2 2
Четверть
град
I
0
45
рад
4
cos α
2
2
sin α
2
2
tg α
1

13.

Упражнения
1. Запишите множество чисел, соответствующее
точкам:
2
2 k
3
k
6

14.

Упражнения
1. Запишите множество чисел, соответствующее
точкам:
5
6
2 k
3
2 k, k Z,
6
5
2 k, k Z.
6

15.

у
π/2
М(t)
M(x;y)
у
π
0
α
х
3π/2
2π
х
cos α = x
sin α = y

16.

Основные тригонометрические тождества
у
π/2
М(t)
M(x;y)
cos α = x
sin α = y
у
π
α
х
0 х
2π
х у 1
2
3π/2
2
2
cos 2 sin 2 1

17.

Основные тригонометрические тождества
tg
sin
cos
сtg
tg сtg 1
cos
sin

18.

Знаки косинуса.
II ч
у
III ч
Iч
+
+α
cos( ) cos
0
+
-α
IV ч

19.

Знаки синуса.
II ч
у
+
III ч
Iч
+
0
-
+α
sin ( ) sin
-α
IV ч

20.

Знаки тангенса и котангенса.
II ч
у
Iч
- + +α
0
+
III ч
-
-α
IV ч
tg ( ) tg
сtg ( ) сtg

21.

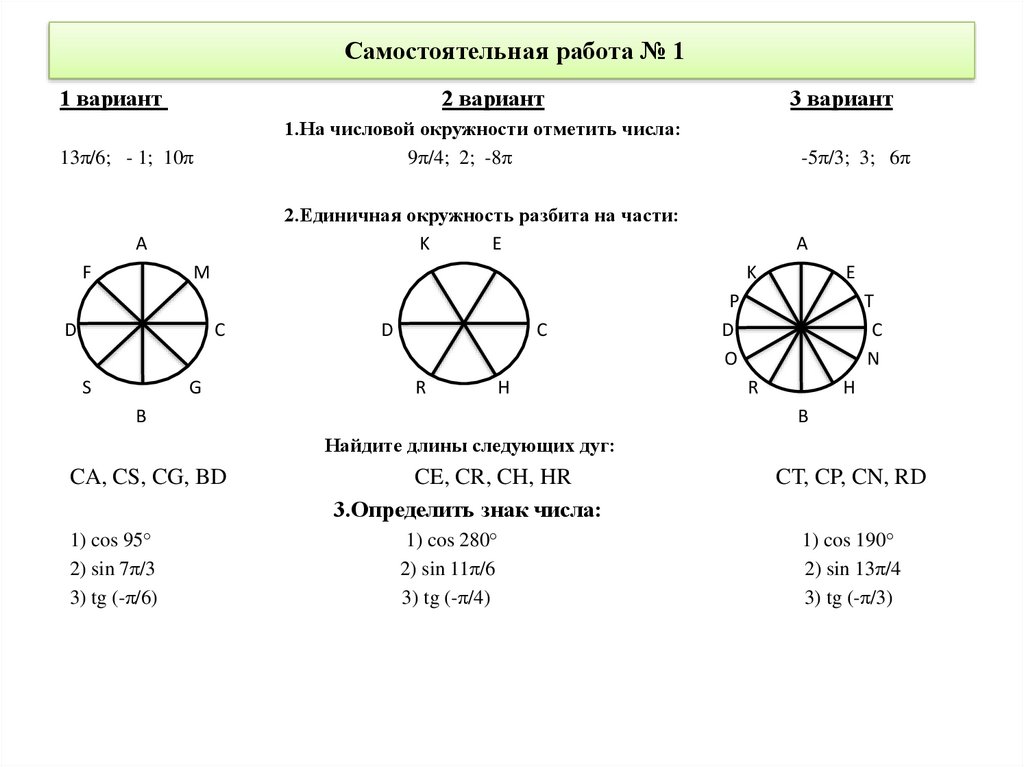
Самостоятельная работа № 1
1 вариант
2 вариант
13π/6; - 1; 10π
A
F
3 вариант
1.На числовой окружности отметить числа:
9π/4; 2; -8π
-5π/3; 3; 6π
2.Единичная окружность разбита на части:
K
E
A
M
D
K
C
S
G
D
C
R
H
B
E
P
D
O
T
C
N
R
H
B
Найдите длины следующих дуг:
CA, CS, CG, BD
1) cos 95°
2) sin 7π/3
3) tg (-π/6)
CE, CR, CH, HR
3.Определить знак числа:
1) cos 280°
2) sin 11π/6
3) tg (-π/4)
CT, CP, CN, RD
1) cos 190°
2) sin 13π/4
3) tg (-π/3)

22.

Синус и косинус. Тангенс и котангенс.

23.

Проверочная работа.

24.

Основные тригонометрические тождества
cos sin 1
2
2
sin 2 1 cos 2
cos 2 1 sin 2
1
1 tg
cos 2
2
1
ctg 1
sin 2
2

25.

26.

27.

1)
2)
3)
4
4)

28.

Простейшие тригонометрические уравнения

29.

Домашнее задание :

30.

31.

32.

33.

34.

д)

35.

36.

Формулы сложения
sin(x + y)= sinx·cosy + siny·cosx
cos(x + y)= cosx·cosy - sinx·siny
sin(x – y)= sinx·cosy - siny·cosx
cos(x – y)= cosx·cosy + sinx·siny
tg x y

37.

Формулы двойного и половинного аргумента
sin2x = 2 sinx·cosx
cos2x = cos²x - sin²x
cos2x = 1 – 2sin²x
cos2x = 2cos²x - 1
1 cos 2 x
tg x
1 cos 2 x
2

38.

Формулы приведения
y
π/2+t
π/2
π/2-t
1). Определить четверть
π–t
2π+t
π
0 x
π+t
2π-t
3π/2-t
3π/2
3π/2+t
2).Определить знак функции в четверти
3). ОХ – не меняем функцию;
ОУ – меняем функцию.

39.

Преобразование сумм тригонометрических функций в произведение
- вспомогательный угол