Геометрические построения

1. ГЕОМЕТРИЧЕСКИЕ ПОСТРОЕНИЯ

2.

Графический способ решения
геометрических задач на
плоскости
при помощи чертежных
инструментов
2

3.

Деление
отрезка на равные части;
Деление
угла на равные части;
Нахождение
Деление
центра дуги;
окружностей на равные
части;
Орнамент
3

4.

Дан отрезок АВ, который
нужно поделить на две
равные части.
4

5.

Из концов отрезка А и В
циркулем проводят две дуги
окружности радиусом R,
несколько большим половины
отрезка, до взаимного
пересечения в точках а и в.
5

6.

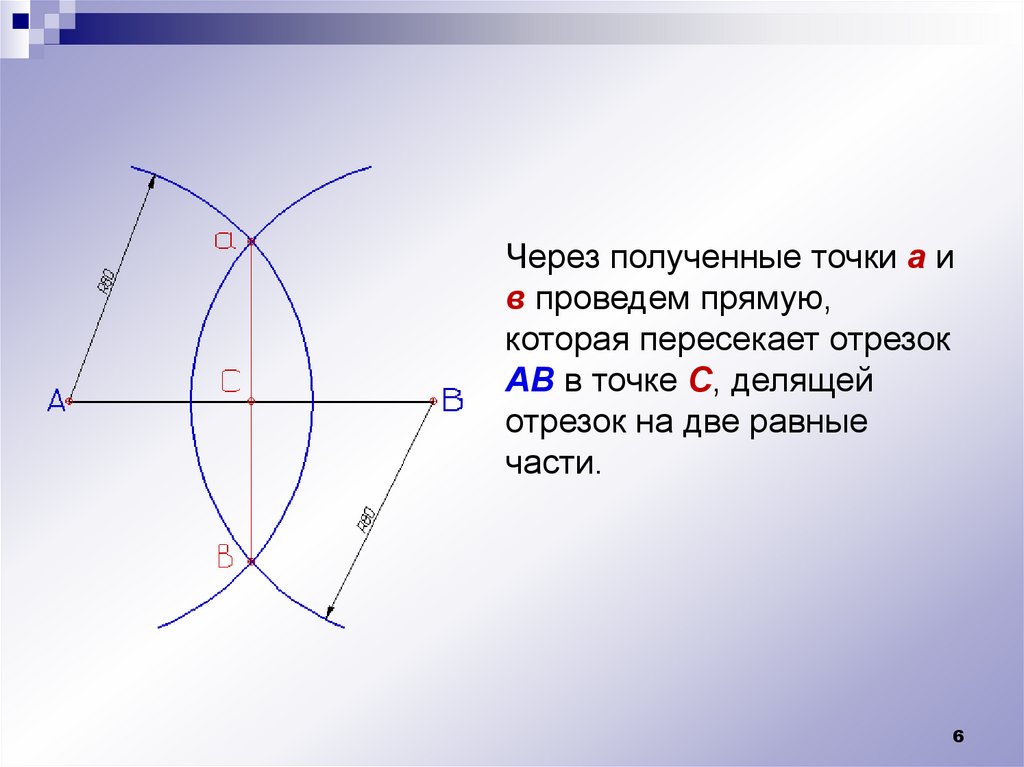
Через полученные точки а и
в проведем прямую,
которая пересекает отрезок
АВ в точке С, делящей
отрезок на две равные
части.
6

7.

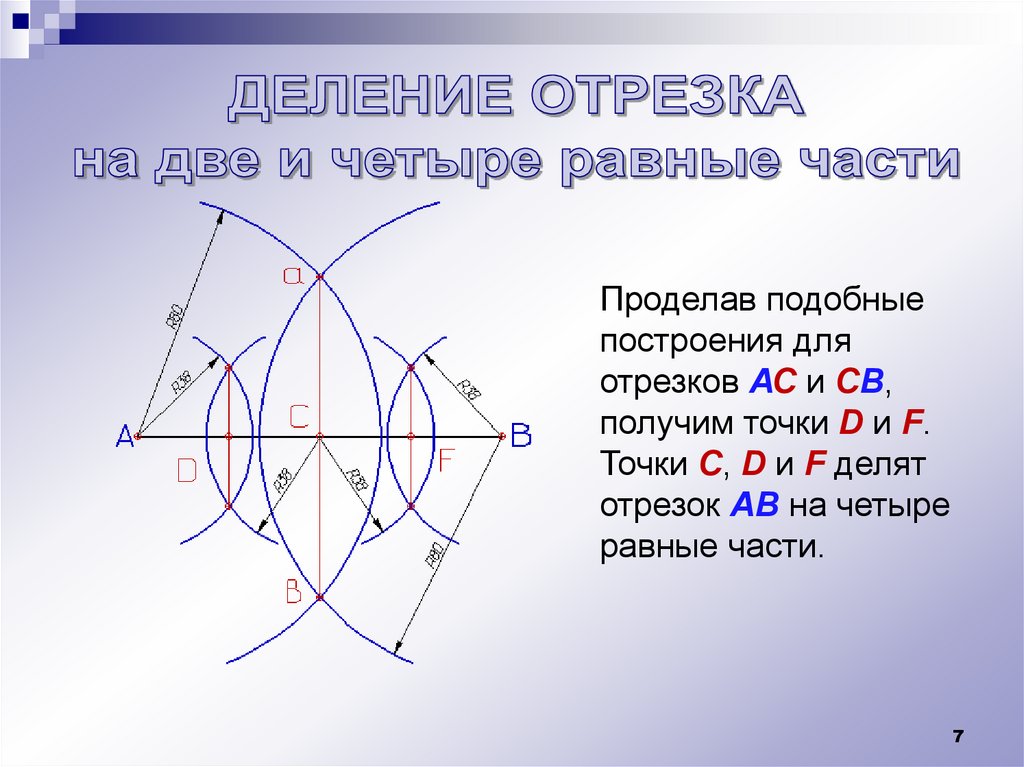
Проделав подобные
построения для
отрезков АС и СВ,
получим точки D и F.
Точки С, D и F делят
отрезок АВ на четыре
равные части.
7

8.

А
1'
1
2'
3'
4'
В
2
3
4
С
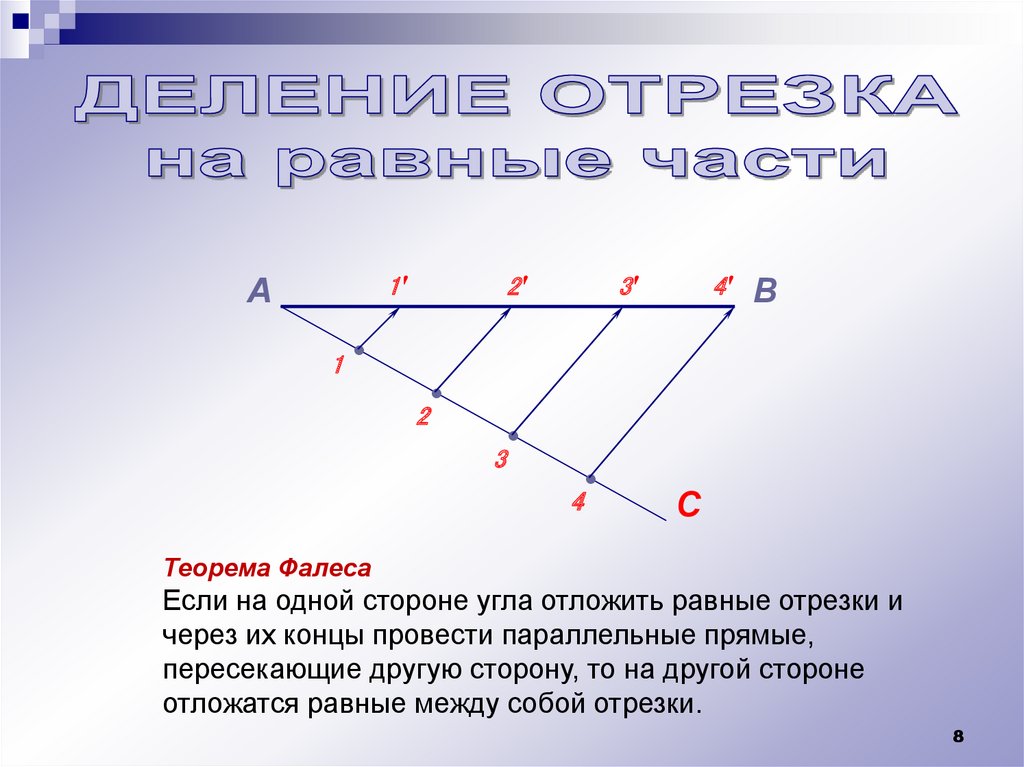
Теорема Фалеса
Если на одной стороне угла отложить равные отрезки и
через их концы провести параллельные прямые,
пересекающие другую сторону, то на другой стороне
отложатся равные между собой отрезки.
8

9.

Дан угол АВС, который
необходимо разделить на две
равные части.
Для того чтобы разделить
угол АВС пополам нужно
провести биссектрису из
вершины угла.
9

10.

Построение биссектрисы
выполняется в следующей
последовательности:
Из вершины угла проводят
дугу окружности
произвольного радиуса r
до пересечения со
сторонами угла в точках D
и F;
10

11.

Из полученных точек
проводят две дуги
радиусом R, величина
которого больше половины
длины дуги DF, до
взаимного пересечения в
точке К;
Прямая проходящая через
вершину В и точку К биссектриса данного угла
т.е. делит угол на две
равные части.
11

12.

Дан угол АВС, который необходимо
разделить на три равные части.
12

13.

Деление прямого угла
АВС на три равные части
выполняется в
следующей
последовательности:
Из вершины угла
проводят дугу окружности
произвольного радиуса R
до пересечения со
сторонами угла в точках
D и F;
13

14.

Из полученных точек проводят
две дуги тем же радиусом
R, до взаимного пересечения
с дугой DF в точках К и М;
Точки К и М соединяют с
вершиной А прямыми,
которые разделят угол АВС на
три равные части.
14

15.

Дана дуга окружности.
Необходимо найти центр
и радиус окружности .
15

16.

Нахождение положения
центра и величины радиуса
данной дуги окружности
выполняется в следующей
последовательности:
1. На дуге
произвольно выбирают три
точки A, В и С;
16

17.

2. Соединяют выбранные
точки отрезками (хордами);
К отрезкам АВ и ВС через их
середины восстанавливают
перпендикуляры;
17

18.

К отрезкам АВ и ВС через их
середины восстанавливают
перпендикуляры;
18

19.

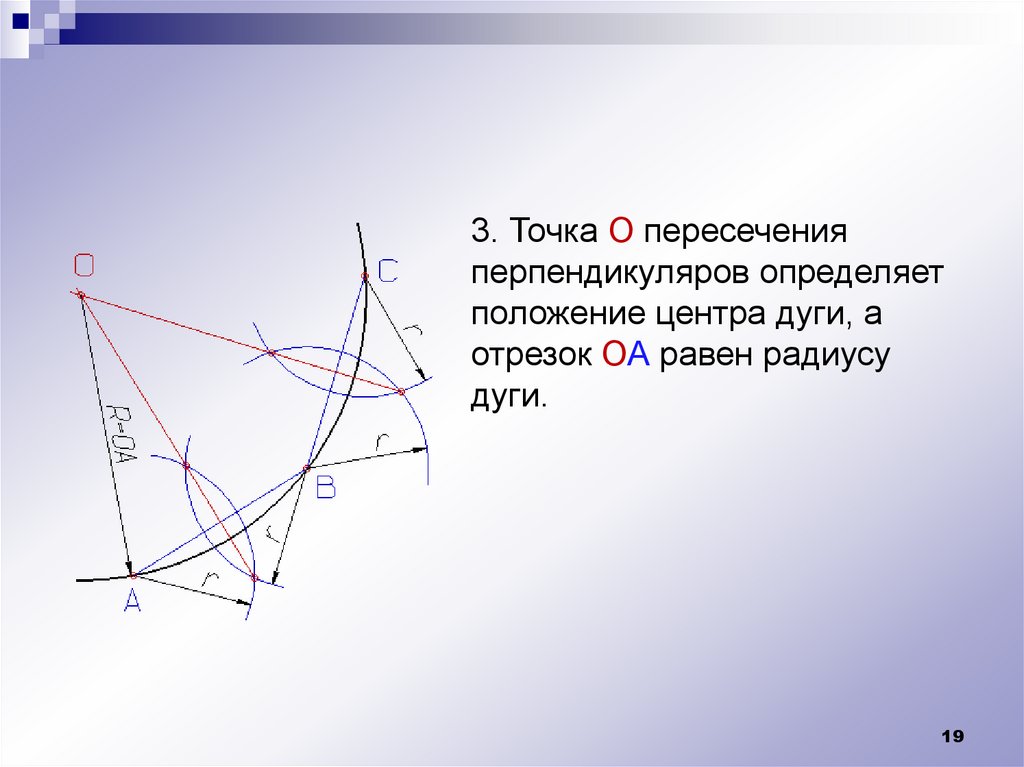
3. Точка О пересечения
перпендикуляров определяет
положение центра дуги, а
отрезок ОА равен радиусу
дуги.
19

20.

2
2
5
6
1
3
О
1
8
4
3
•7
4
20

21.

21

22.

2
2
7
1
3
5
6
4
8
1
3
5
6
4
22

23.

23

24.

24

25.

а
5
2
6
10
9
3
1
с
в
11
12
7
4
8
d
25

26.

26

27.

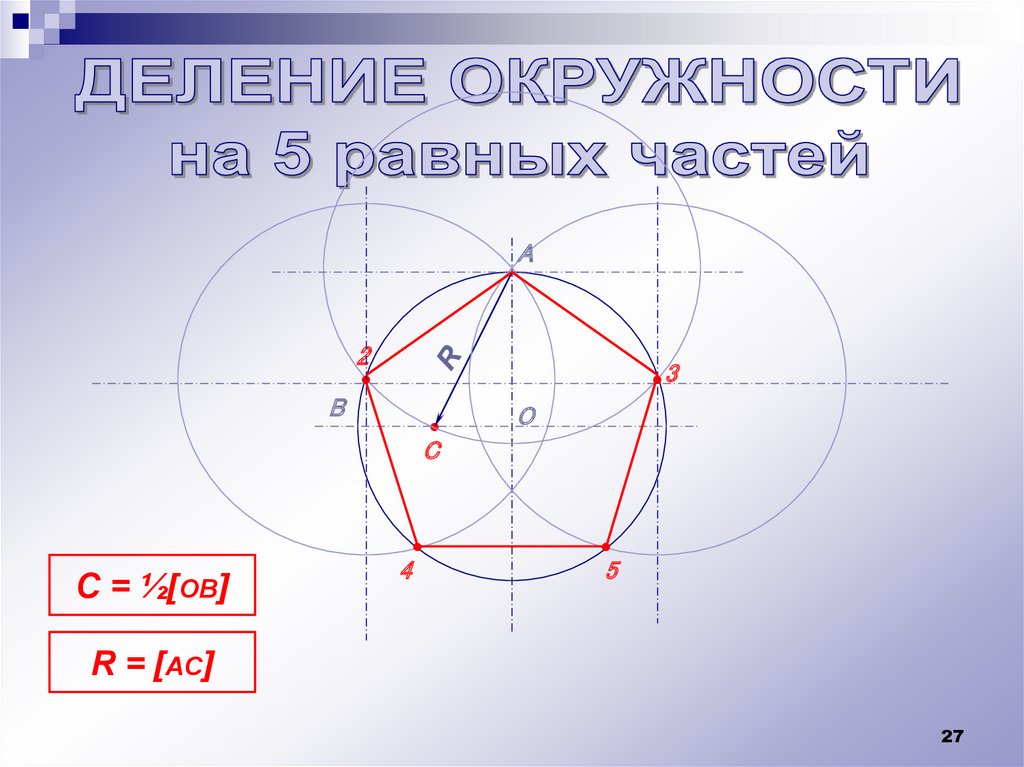
A
2
B
•3
O
C
C = ½[OB]
4
5
R = [AC]
27

28.

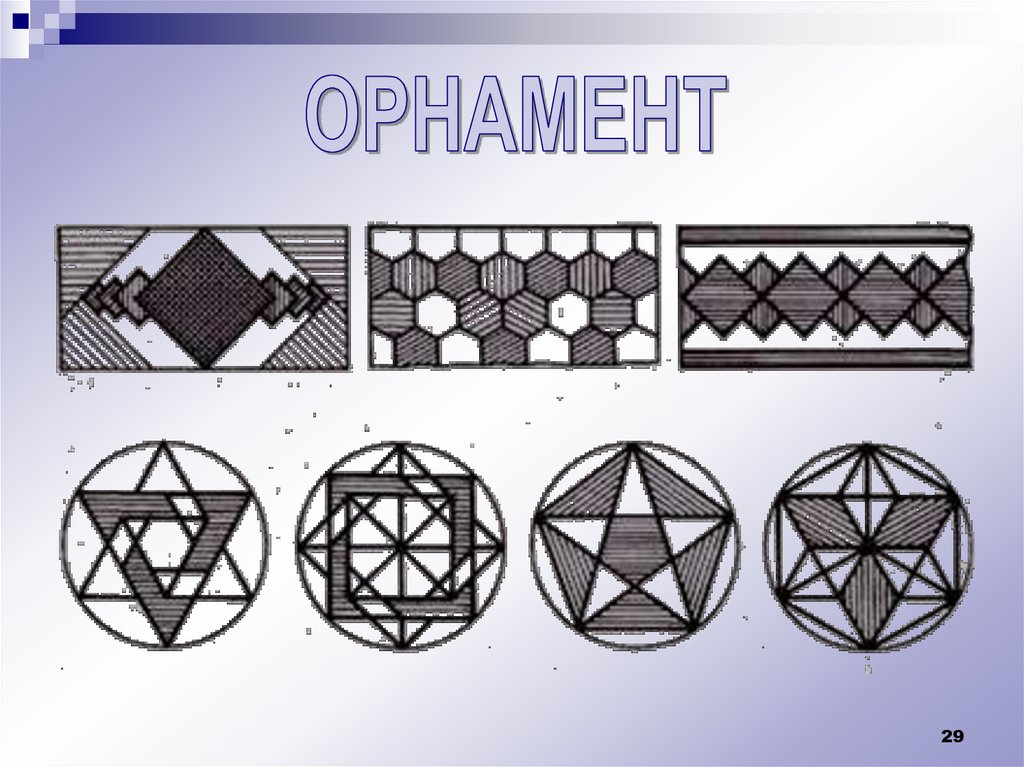
28

29.

29

30.

Читать Т.А. Астахова, К.А. Вольхин
«Геометрические основы построения
чертежа» на сайте кафедры
2. Вычертить в рабочей тетради
орнамент, состоящий
из простейших
геометрических фигур
1.
30