Similar presentations:
Комплексные числа
1. Комплексные числа
2. Основные понятия
Комплексным числомвыражение вида
z
называется
z i
– действительные числа,
где
и
а i – мнимая единица.
i 1
2
3.
Два комплексных числаz1 1 i 1
z2 2 i 2
называются равными ( z1 z 2 ) тогда и
только тогда, когда
1 2
1 2
Комплексное число z1 1
равно 0 тогда и только тогда, когда
1 0,
1 0
i 1
4.
Понятия «больше» и «меньше» длякомплексных чисел не определяются.
Два комплексных числа
z i , z i
называются сопряженными.
Справедливо равенство
z z
2
2
5. Извлечение корней из комплексных чисел
Корнем n-ой степени из комплексногочисла z называется комплексное число w,
удовлетворяющее равенству
w z
n
Т.е.
n
z w , если w z
n
6. Пример
1. Вычислить 42. Решить уравнение
3. Решить уравнение
x 25 0
2
x 2x 5 0
2
Решение. 1.
4
4 i 2i
2
7.
2.x 25 0 x 25
x 25 5i
2
2
x 2x 5 0
2
D ( 2) 4 5 16
2 16 2 4i
x1
1 2i
2
2
2 16
x2
1 2i
2
3.
2
8. Тема: ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
§1. Дифференциальныеуравнения первого порядка
9. Дифференциальные уравнения первого порядка
F ( x, y, y' ) 0Уравнение
связывающее независимую переменную x,
искомую функцию y и ее производную y’,
называется
дифференциальным уравнением первого
порядка
(ДУ первого порядка).
10.
Если дифференциальное уравнениеможно записать в виде y ' f ( x, y )
то говорят, что оно разрешимо относительно
производной.
Это уравнение можно записать в виде
dy
так как y '
dx
dy f ( x, y)dx
или, в более общем виде
P( x, y)dx Q( x, y)dy 0
11. Решение дифференциального уравнения
Решением(или
интегралом)
дифференциального уравнения первого
порядка называется любая функция y (x),
которая при подстановке в уравнение
обращает его в тождество.
График функции в этом случае
называется интегральной кривой.
Процесс нахождения решений данного
дифференциального уравнения называется
интегрированием этого уравнения.
12. Задача Коши
Задачаотыскания
решения
дифференциального
уравнения,
удовлетворяющего заданному начальному
условию y ( x 0 ) y 0 , называется задачей
Коши.
Задача Коши:
y' f ( x, y)
y ( x0 ) y 0
13. Общее решение ДУ
Общим решением дифференциальногоуравнения F ( x, y, y' ) 0
называется такая функция y ( x, C )
где – C произвольная постоянная, что при
любом конкретном
C
она является
решением дифференциального уравнения;
для любого допустимого начального условия
y ( x 0 ) y 0 найдется такое C C 0 , что
( x0 , C0 ) y 0
14.
Если общее решение записать в виде( x, y, C ) 0
то это соотношение называется общим
интегралом
дифференциального
уравнения.
Частным решением
дифференциального уравнения первого
порядка называется функция y ( x, C 0 )
которая получается из общего решения при
конкретном значении C.
15. Дифференциальные уравнения с разделяющимися переменными
Уравнение видаP1 ( x )Q1 ( y )dx P2 ( x )Q2 ( y )dy 0 (1)
Где P1 ( x ) P2 ( x ) Q1 ( y ) Q2 ( y )
–
заданные
функции,
называется
дифференциальным
уравнением
с
разделяющимися переменными.
16.
Если Q1 ( y ) 0 P2 ( x) 0то, разделив уравнение (1) на P2 ( x)Q1 ( y )
получим уравнение
P1 ( x )
Q2 ( y )
dx
dy 0
(2)
P2 ( x )
Q1 ( y )
которое называется дифференциальным
уравнением
с
разделенными
переменными (коэффициент при dx есть
функция переменной x, при dy – функция
переменной y).
17.
Общийинтеграл
уравнения
находится
интегрированием:
полученного
почленным
P1 ( x )
Q2 ( y )
P2 ( x ) dx Q1 ( y ) dy C
Уравнение
y' P( x)Q( y)
Где P( x), Q( y )
– заданные функции,
сводится к уравнению (2).
dy
Нужно положить y'
и разделить
dx
переменные
18. Схема решения ДУ с разделяющимися переменными
ЭтапыПример для уравнения
( x xy )dx ( y yx )dy 0
2
1.
Приводим
заданное уравнение
к виду (1). Для этого
вынесем из скобок
общие множители
2
x(1 y )dx y(1 x )dy 0
2
2
2. Разделим пере2
2
x
(1
y
)
dx
y
(1
x
)dy
менные, выполнив
0
2
2
2
2
деление обеих частей (1 y )(1 x ) (1 y )(1 x )
уравнения
на
произведение(1 y 2 )(1 x 2 )
19.
3. Сократив дроби,получим уравнение с
разделенными
переменными
4.
Интегрируем
полученное
уравнение
ln x ln y ln xy
1
C1 ln C
2
xdx
ydy
0
2
2
1 x
1 y
,,
,
где ,
,
,.
xdx
ydy
1 x 2 1 y 2 C1
1
1
1
2
2
ln(1 x ) ln(1 y ) ln C
2
2
2
(1 x )(1 y ) C
2
2
20. Линейные дифференциальные уравнения первого порядка
Дифференциальное уравнение видаy' p( x) y g ( x) (3)
Где g ( x) 0 , p(x) , g (x )
– непрерывные функции, называется
линейным неоднородным уравнением
первого порядка.
21. §2. Дифференциальные уравнения второго порядка
Уравнение видаF ( x, y, y' , y' ' ) 0 или y' ' f ( x, y, y' )
называется дифференциальным
уравнением второго порядка.
Начальные условия для данного
уравнения имеют вид
'
y0
y ( x0 ) y0 , y ' ( x0 )
'
x0 , y0 , y 0 – некоторые числа.
22.
Решением уравнения y' ' f ( x, y, y' )называется всякая функция , которая при
подстановке вместе с y’ и y’’ в это уравнение
обращает его в тождество.
Пример. Показать, что функция y cos8 x
является решением уравнения y '' 64 y 0
Решение. y ' 8sin8 x, y '' 64cos8 x
y '' 64 y 64cos8x 64cos8x 0
23.
Общим решением уравненияy' ' f ( x, y, y' )
называется функция
y ( x, C1 , C 2 ) ,
зависящая от двух произвольных постоянных
C1 и C 2 и такая, что:
1) она является решением уравнения при
любых конкретных значениях C1 и C 2 ;
2) для любых допустимых начальных условий
можно подобрать такие C10 и C 20 , что
функция y ( x, C10 , C 20 ) будет удовлетворять
этим условиям.
24. Понижение порядка дифференциальных уравнений
В некоторых частных случаях удаетсяпонизить порядок дифференциального
уравнения второго порядка. В итоге
дифференциальное уравнение приводится
к дифференциальному уравнению первого
порядка одного из ранее изученных типов.
25. Типы уравнений, допускающих понижение порядка
Уравнениеy ' ' f ( x)
Способ понижения порядка
y' f ( x)dx F ( x) C1
y ( F ( x) C1 )dx C2
26. Пример
Найти общее решение уравнения2
y ' ' x sin 3x
Решение. Интегрируя, получим
2
y' ( x sin 3x)dx C1
2
y' x dx sin 3xdx C1
3
x
1
y'
cos 3 x C1 – уравнение с
3 3
разделяющимися переменными.
27.
dyТак как y '
dx
разделяем переменные и интегрируем:
x3 1
dy
cos 3x C1 dx
3 3
x3 1
y cos 3x C1 dx C 2
3 3
1 4 1
y x sin 3x C1 x C 2
12
9
28. ИНТЕГРИРОВАНИЕ ДУ ВТОРОГО ПОРЯДКА С ПОСТОЯННЫМИ КОЭФФИЦИЕНТАМИ
Уравнение вида y '' py ' qy 0, (4)(p и q – постоянные) называется линейным
однородным
дифференциальным
уравнением
с
постоянными
коэффициентами.
29.
Уравнение k pk q 0называется
характеристическим
дифференциального уравнения
2
для
y '' py ' qy 0.
Для составления характеристического
уравнения в уравнении (4) заменяют
y k , y k ,
2
y 1.
Вид общего решения этого уравнения
определяется корнями характеристического
уравнения k 1 и k 2 .
30. Пример
Составить характеристические уравнения дляследующих дифференциальных уравнений:
1. 3 y '' 5 y ' 6 y 0,
y '' 3 y ' y 0,
2.
7 y '' 2 y 0,
3.
y '' 9 y ' 0.
4.
31.
Корнихарактеристиче
ского уравнения
1. k1 k 2
– действительные
числа
( D 0 )
2. k k
1
2
– действительные
числа ( D 0)
Форма общего решения
уравнения (4):
y C1e
k1 x
C2e
k2 x
y e (C1 C2 x )
k1 x
32.
3.k1, 2 i
x
–
комплексные y e (C1 cos x C 2 sin x )
числа ( D 0 )
33. Пример
1. Найти общее решение уравненияy' ' 5 y' 6 y 0
Решение. Составим характеристическое
уравнение, заменяя в данном уравнении
y '' k
2
y' k
y 1
Получим
2
k 5k 6 0
34.
Найдем дискриминант квадратногоуравнения:
2
2
D b 4ac 5 4 1 6 1
b D
k1,2
, k1 2, k 2 3,
2a
k1 k 2
Имеем случай 1, следовательно,
y C1e C2e
2x
3x
– общее решение уравнения.






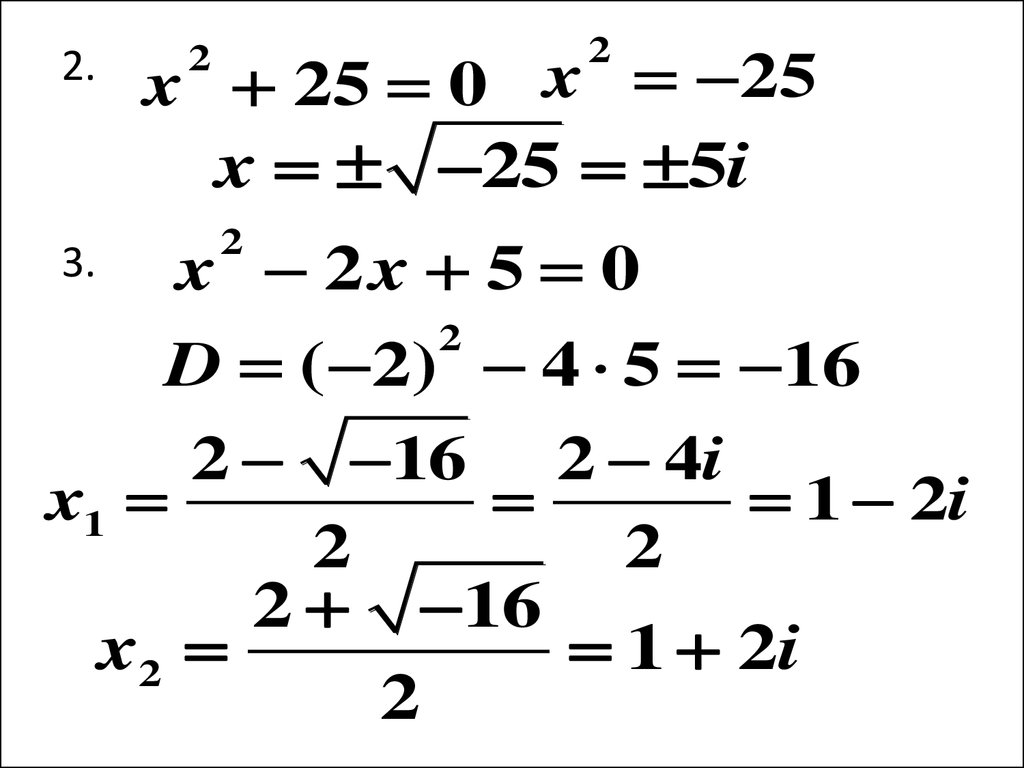



























 mathematics
mathematics








