Кути у просторі

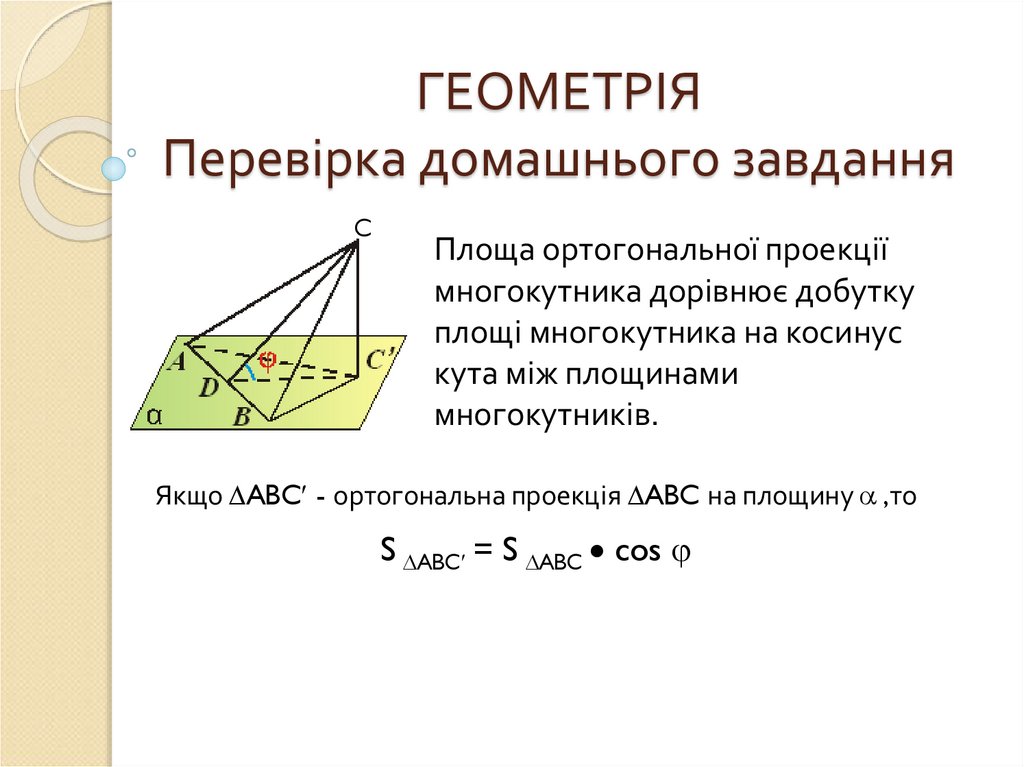
1. ГЕОМЕТРІЯ Перевірка домашнього завдання

C
Площа ортогональної проекції
многокутника дорівнює добутку
площі многокутника на косинус
кута між площинами
многокутників.
Якщо ABC - ортогональна проекція ABC на площину ,то
S ABC = S ABC cos

2.

Кути у просторі

3. Вимірювання відстаней у просторі: від точки до прямої від точки до площини від прямої до площини між площинами

4. Основні фігури простору: точка, пряма, площина

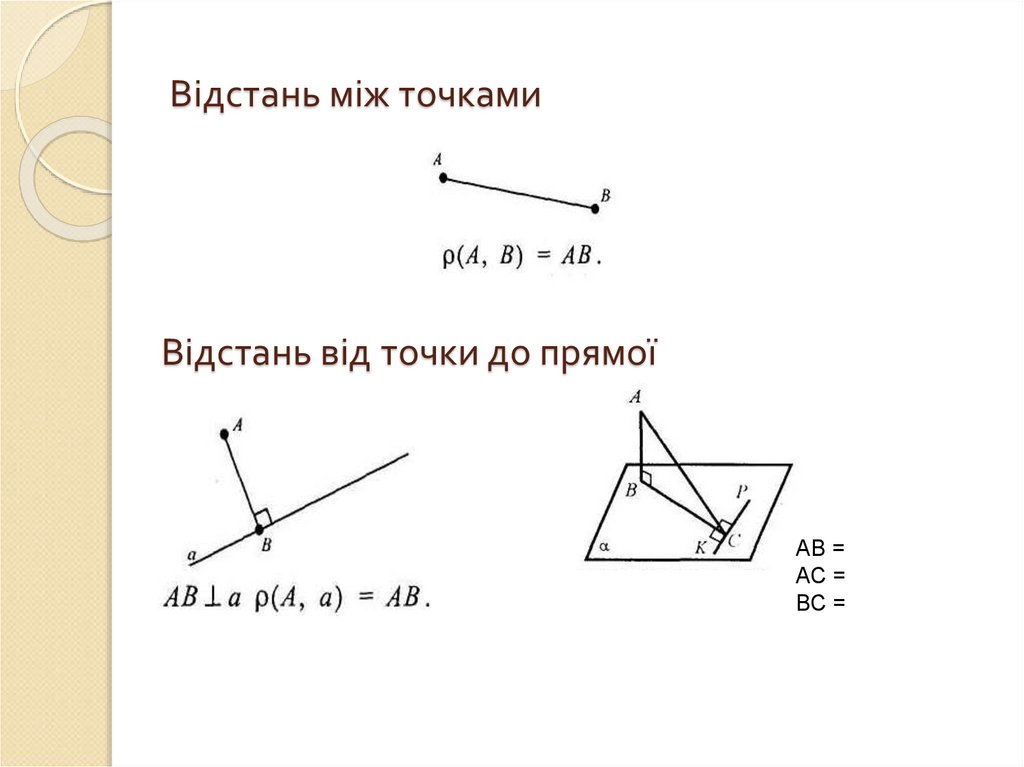
5. Відстань між точками

Відстань від точки до прямої
АВ =
АС =
ВС =

6. Завдання 1. З точки М опустити перпендикуляр на пряму АВ. Вказати  (М; (АВС))

Завдання 1. З точки М опустити перпендикуляр на
пряму АВ. Вказати (М; (АВС))

7.

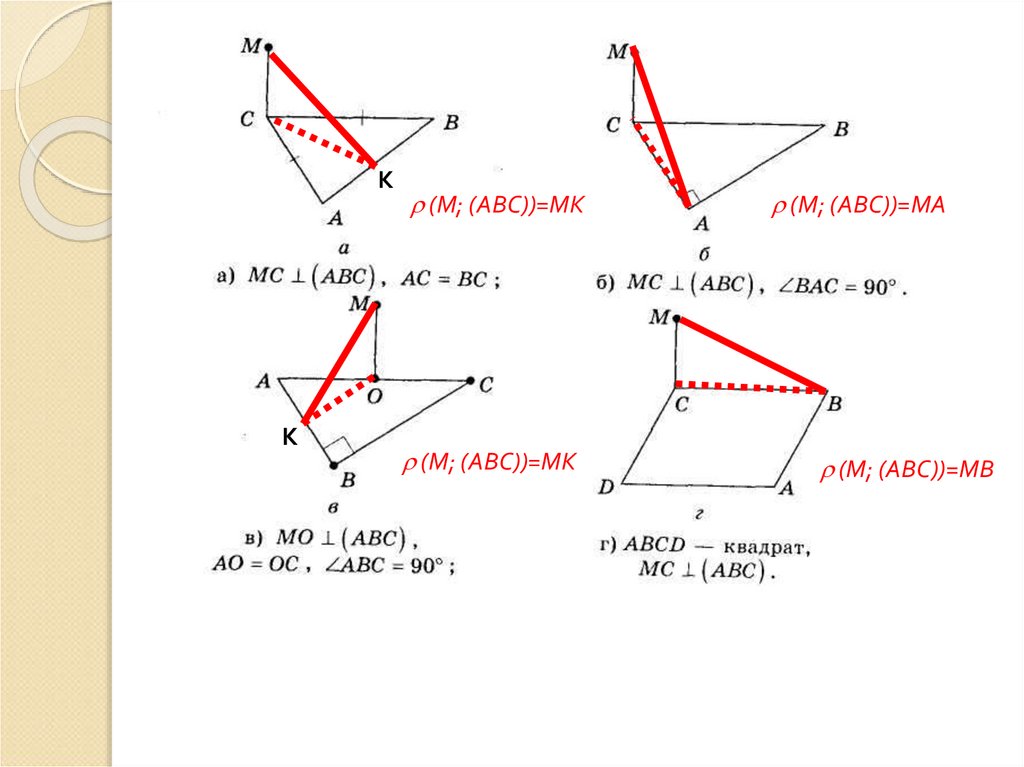
К
К
(М; (АВС))=МК
(М; (АВС))=МК
(М; (АВС))=МА
(М; (АВС))=МВ

8.

Як розміщуються дві прямі у просторі?
Які розташуються на відстані?

9.

ПАРАЛЕЛЬНІ ПРЯМІ
Відстань між паралельними прямими
– це відстань від якої-небудь точки
однієї прямої до другої.
МИМОБІЖНІ ПРЯМІ
Відстанню між мимобіжними прямими
називається довжина їхнього спільного
перпендикуляра - відрізок із кінцями на цих
прямих, перпендикулярний до кожної з них.

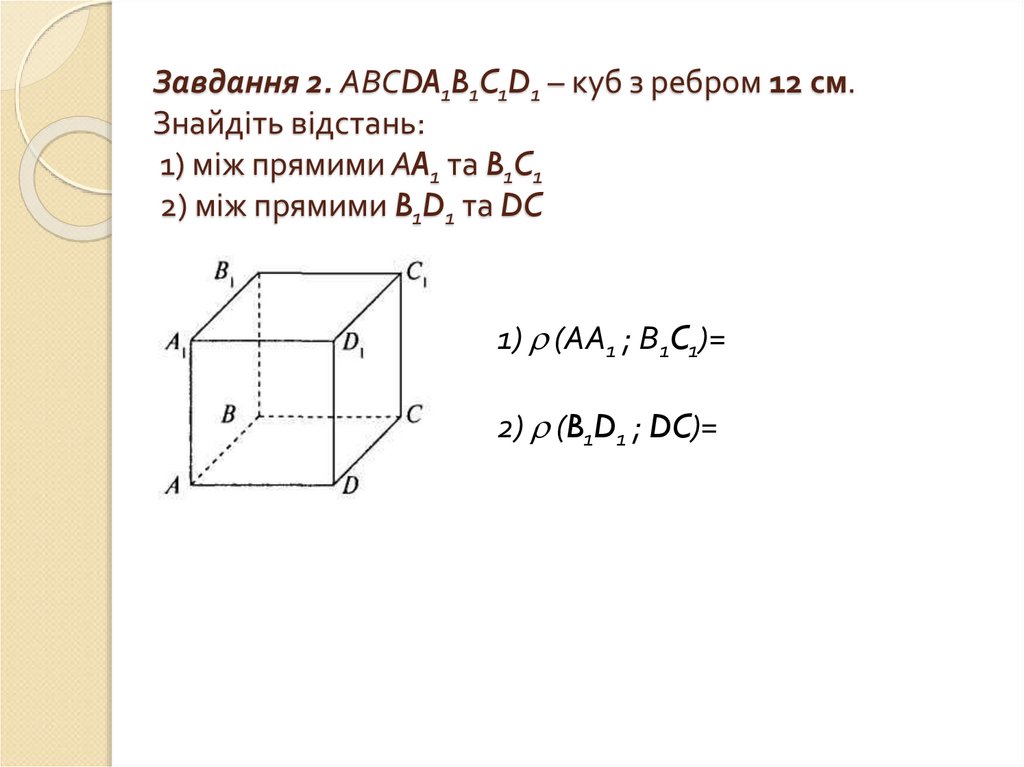
10. Завдання 2. АВСDA1B1C1D1 – куб з ребром 12 см. Знайдіть відстань: 1) між прямими АA1 та B1C1 2) між прямими B1D1 та DC

1) (АА1 ; В1C1)=
2) (B1D1 ; DC)=

11.

У якому розміщенні прямої та площини можна говорити про відстань?
Відстанню від прямої до паралельної їй площини
називається відстань від будь-якої точки цієї прямої до площини.

12.

У якому розміщенні площин можна говорити про відстань?
Відстанню між паралельними площинами називається відстань від
будь-якої точки однієї площини до другої площини.

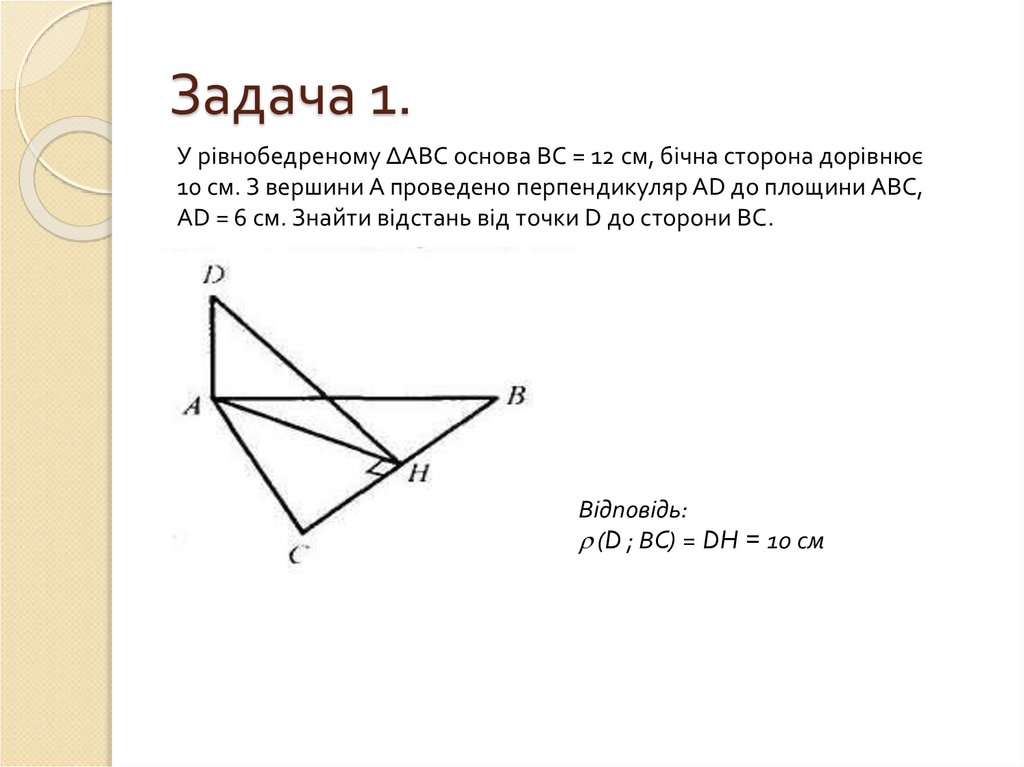
13. Задача 1.

У рівнобедреному ∆АВС основа ВС = 12 см, бічна сторона дорівнює
10 см. З вершини А проведено перпендикуляр AD до площини ABC,
AD = 6 см. Знайти відстань від точки D до сторони BC.
Відповідь:
(D ; ВC) = DH = 10 см

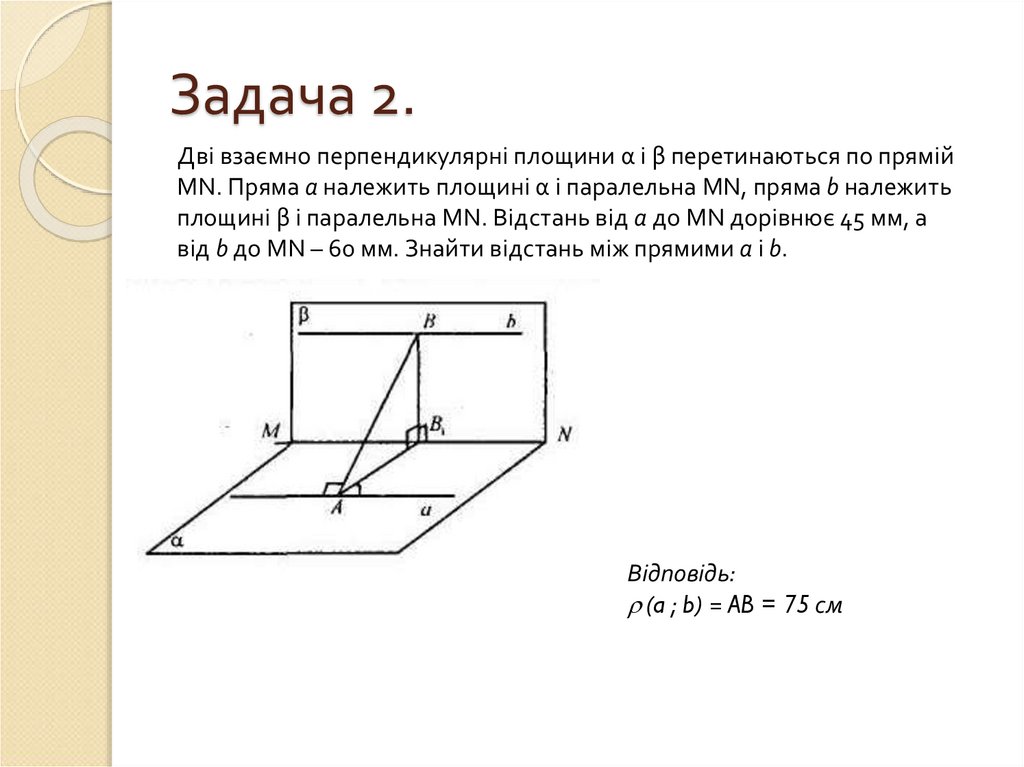
14. Задача 2.

Дві взаємно перпендикулярні площини α і β перетинаються по прямій
MN. Пряма а належить площині α і паралельна MN, пряма b належить
площині β і паралельна MN. Відстань від а до MN дорівнює 45 мм, а
від b до MN – 60 мм. Знайти відстань між прямими а і b.
Відповідь:
(a ; b) = AB = 75 см

15.

ДОМАШНЄ ЗАВДАННЯ:
Розв'яжіть задачі 1 і 2
зі слайдів 13 і14