Similar presentations:
Математика. Раздел 6. Метод координат в пространстве. Занятие 65. Простейшие задачи в координатах
1.
МатематикаРаздел 6. Метод координат в пространстве
Занятие 65.
Простейшие задачи в
координатах
2.
Простейшие задачи в координатахПусть даны точки А ( x1 ; y1 ; z1 )
Тогда:
1.
В ( x2 ; y 2 ; z 2 )
АВ ( x2 x1 ; y2 y1 ; z 2 z1 )
2. АВ ( x2 x1 ) 2 ( y2 y1 ) 2 ( z 2 z1 ) 2
3. Если М ( x; y; z ) середина АВ, то
x1 x2
y1 y2
z1 z 2
х
; у
; z
2
2
2
4. Если a ( x; y; z ), то a x 2 y 2 z 2
5. cos
аb
а b
, где (а; b)
3.
Простейшие задачи в координатахДаны точки: А ( 4; 6; 1) В (0; 2; 5) С (3; 1; 1)
1. Вычислить координаты векторов:
0 4 0 4 4
АВ 2 6 2 6 8
5 1 5 ( 1) 6
3 0 3
ВС 1 2 3
1 5 4
3 4
АС 1 6
1 1
1
5
2
2. Вычислить длины векторов:
АВ ( 4) 2 ( 8) 2 6 2 16 64 36 116 2 29
АС ( 1) 2 ( 5) 2 2 2 1 25 4 30
4.
Простейшие задачи в координатахДаны точки: А ( 4; 6; 1) В (0; 2; 5) С (3; 1; 1)
3. Вычислить длину медианы СМ из АВС
Если СМ медиана, то М = (х; у; z) середина АВ
4 0
6 ( 2)
х
2; у
2;
2
2
т.е. М = (2; 2; 2)
1 5
z
2
2
СМ (2 3) 2 (2 1) 2 (2 1) 2 1 1 1 3
5.
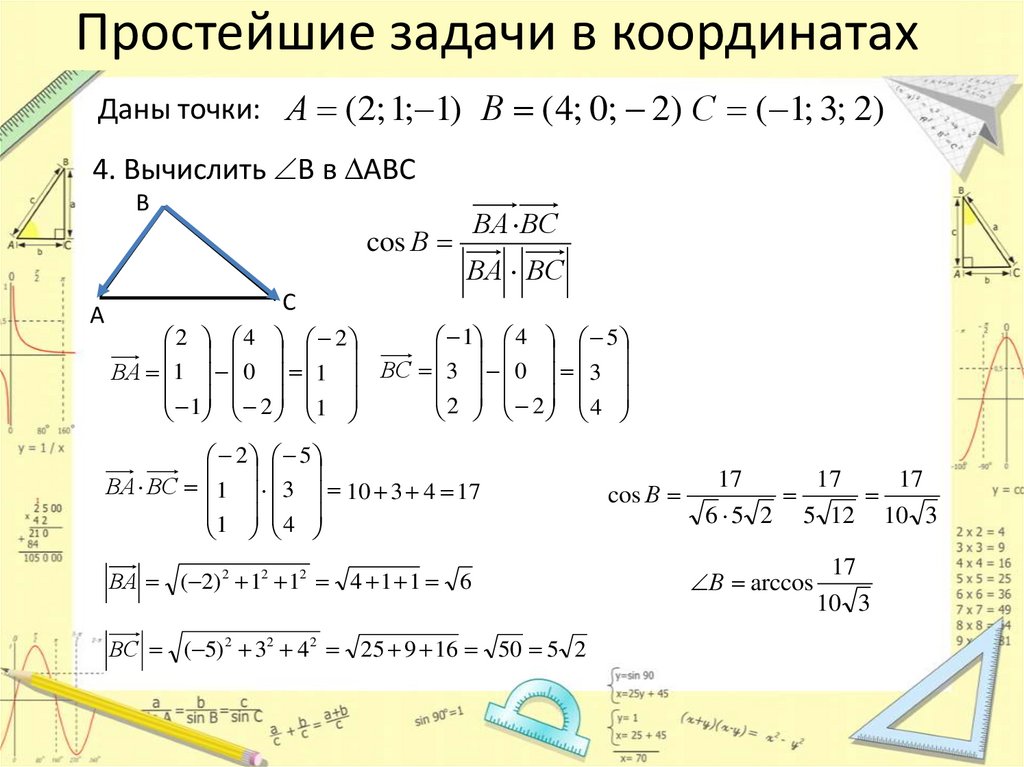
Простейшие задачи в координатахДаны точки: А ( 2; 1; 1) В ( 4; 0; 2) С ( 1; 3; 2)
4. Вычислить В в АВС
В
cos В
А
ВА ВС
ВА ВС
С
2 4 2
ВА 1 0 1
1 2 1
1 4 5
ВС 3 0 3
2 2 4
2 5
ВА ВС 1 3 10 3 4 17
1 4
ВА ( 2) 2 12 12 4 1 1 6
ВС ( 5) 2 32 4 2 25 9 16 50 5 2
cos В
17
17
17
6 5 2 5 12 10 3
В arccos
17
10 3
6.
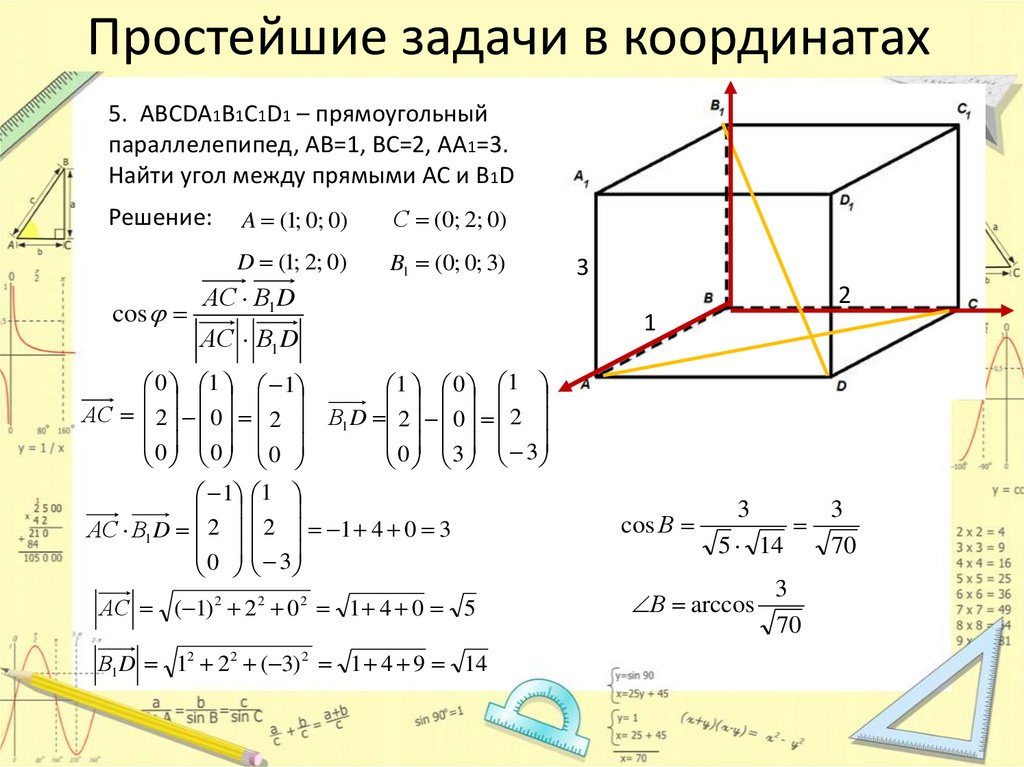
Простейшие задачи в координатах5. АВСDA1B1C1D1 – прямоугольный
параллелепипед, АВ=1, ВС=2, АА1=3.
Найти угол между прямыми АС и B1D
Решение:
cos
A (1; 0; 0)
С (0; 2; 0)
D (1; 2; 0)
B1 (0; 0; 3)
АC В1 D
2
1
АC В1 D
0 1 1
АC 2 0 2
0 0 0
1
АС В1 D 2
0
1 0 1
В1 D 2 0 2
0 3 3
1
2 1 4 0 3
3
АС ( 1) 2 0 1 4 0 5
2
2
3
2
В1 D 12 2 2 ( 3) 2 1 4 9 14
cos В
3
3
5 14
70
В arccos
3
70
7.
Шмельков Владимир Юрьевичпреподаватель математики
ГБПОУ ЗКНО
Москва, 2021г.





 mathematics
mathematics








