Параметрический анализ. Параметрические модели функционирования типовых радиоустройств. (Лекция 2)

1.

Дисциплина
«Основы компьютерного проектирования и
1
моделирования радиотехнических систем »
Лекция №2
ОБЩИЕ СВЕДЕНИЯ О ПАРАМЕТРИЧЕСКОМ АНАЛИЗЕ. ПАРАМЕТРИЧЕСКИЕ
МОДЕЛИ ФУНКЦИОНИРОВАНИЯ ТИПОВЫХ РАДИОУСТРОЙСТВ
Цель:
1. Формирование теоретических основ по общим вопросам, связанным
технологиями параметрического моделирования .
2. Изучить концепцию линейного предсказания, типовые модели сигналов,
используемые в моделях РТС и связанные с ними методы параметрической
оптимизации преобразователей .
Учебные вопросы:
1. Общие вопросы параметрического моделирования.
2. Линейное предсказание.
3. Вопросы, связанные с генерацией сигналов в моделях.
4. Методы параметрической оптимизации
Задание на самоподготовку:
Проработать материал лекции по [1] с.115-125 , дополнить конспект лекций методами
генерации случайных чисел, используемых в компьютерных моделях РТС [1].
с

2.

1. Общие вопросы параметрического моделирования
2
Под параметрическим моделированием понимаются выбор некоторой
математической модели случайного процесса и последующий подбор параметров этой
модели для обеспечения максимального соответствия между сигналом, формируемым
моделью, и имеющейся в наличии реальной выборкой данных.
Одной из широко используемых на практике является авторегрессионная (AR)
модель, в которой случайный сигнал формируется путем пропускания дискретного белого
шума через “чисто рекурсивный” (то есть не использующий задержанных отсчетов
входного сигнала) формирующий фильтр.
Если в нашем распоряжении имеется оценка комплексного коэффициента
передачи системы на различных частотах, можно построить реализуемую модель
системы, частотная характеристика которой будет максимально близкой к измеренной.
Под реализуемостью системы здесь подразумевается представимость ее
функции передачи в виде дробно-рациональной функции с заданными порядками
полиномов числителя и знаменателя.
Параметрическое моделирование в данном случае сводится к нахождению
оптимальных коэффициентов полиномов числителя и знаменателя функции
передачи.

3.

2. Линейное предсказание
3
Сигналы в РТС для минимизации ошибок представляются в
ортогональном базисе через линейную композицию:
y (t ) ai P(t )i
i 0
Для реализации процедуры ортогонального представления исходных данных
необходимо выдерживать следующие правила:
- относительно цифровых сигналов для минимизации ошибок представления
необходимо использовать отображение в пространстве дискретных базисов (базис
функций Уолша или реализация метода главных компонент);
- относительно радиосигналов необходимо решать задачу представления в одном
из непрерывных базисов конечных сигналов (базис полиномов Лежандра или
полиномов Чебышева или разложение в ряд Тейлора);
- применение спектрального представления наблюдаемого радиосигнала
посредством гармонических попарно ортогональных функций может быть
эффективно при применении известных методов параметрической идентификации в
условиях предварительного выравнивания отдельных искажений, связанных с
анализом огибающей и исключением режимов интерференции сигналов в точке
приема.

4.

2. Линейное предсказание
4
Пусть в качестве ортогонального представления используется механизм
полиномов (такой подход применим для всех рассмотренных выше
ортогональных представлений). Тогда исходный сигнал, назовем его y во
временном представлении будет иметь следующий вид:
y (t ) ai P(t )i ,
i 0
где ai - коэффициенты разложения, а P (t )i - значения i-х базисов в момент
времени t .
Для доказательства состоятельности утверждения относительно
ортогональности получаемого разложения используют его определение:
b
P(t ) P(t )
i
j
dx 0 .
a
Ключевым здесь являются значения границ представленного интеграла
и характер изменения весовых коэффициентов. Относительно первого
замечания необходимо сказать, что для конечных сигналов границы должны
выступать в качестве конкретных значений (обычно их принимают равными
-1 и 1) и не содержать (как в полиномах Эрмита и Лагера).

5.

2. Линейное предсказание
Для нахождения коэффициентов разложения сигналов используется
следующее интегральное представление (для сигнала, наблюдаемого в
течении времени T ):
T
2
T
2
1
ai y(t ) P(t )i dt .
T
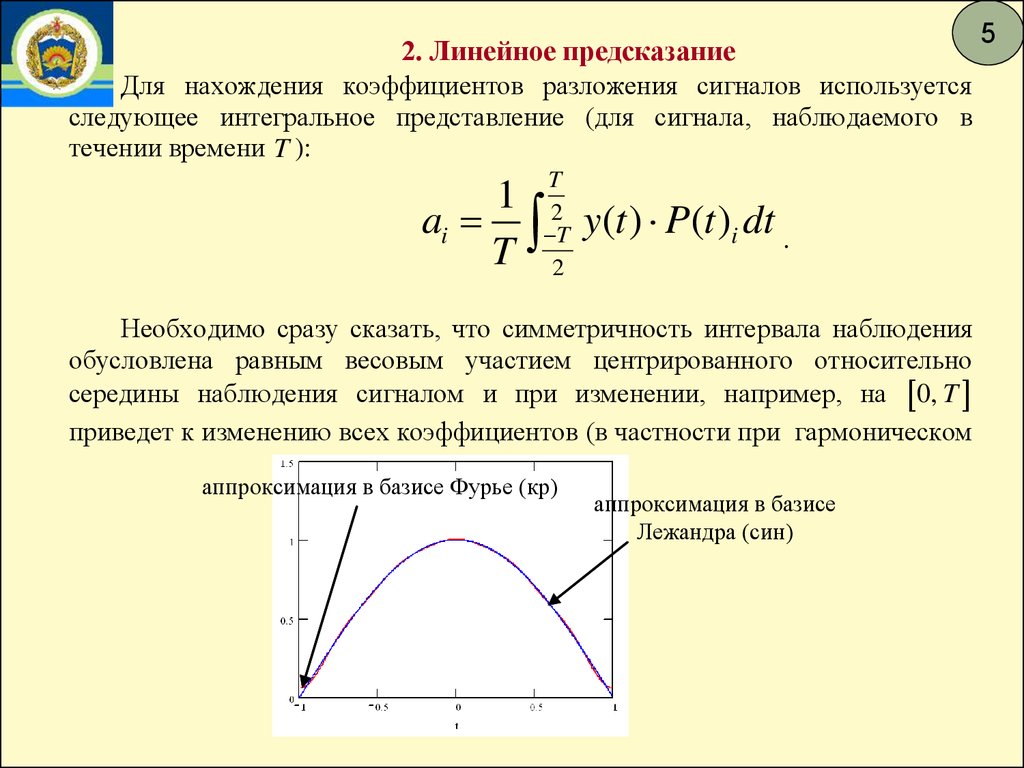
Необходимо сразу сказать, что симметричность интервала наблюдения
обусловлена равным весовым участием центрированного относительно
середины наблюдения сигналом и при изменении, например, на 0, T
приведет к изменению всех коэффициентов (в частности при гармоническом
аппроксимация в базисе Фурье (кр)
аппроксимация в базисе
Лежандра (син)
5

6.

6
2. Линейное предсказание
Использование базиса Фурье
1
s ( t) sin
t 1
2
2
a( i) s ( t) cos ( i w t) d t
T 1
a( 0) 1.273
1
2
b ( i) s ( t) sin ( i w t ) d t
T 1
1
s( t )
0.5
SS( t)
a( 0)
2
5
i
0
1
0
b ( 1) 0
( a( i) cos ( i w t ) b ( i) sin ( i w t) )
1
1
t
T 2
w 2
T
SS ( t)
1
s( t )
0
1
0
t
1

7.

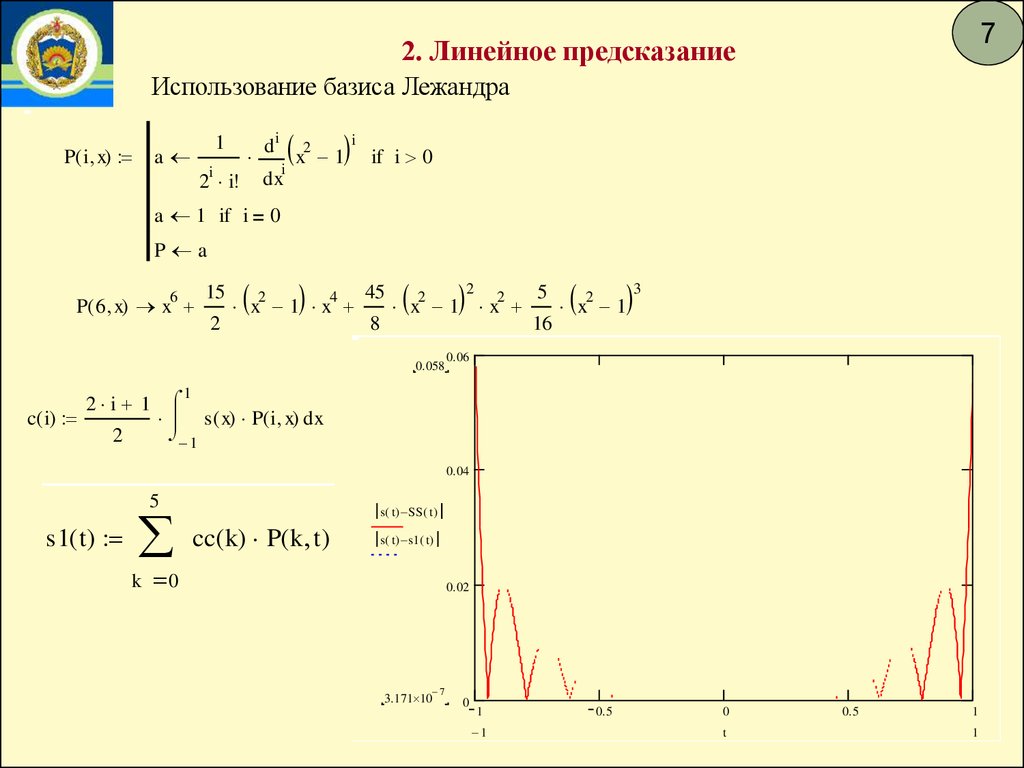
7
2. Линейное предсказание
Использование базиса Лежандра
P( i x)
1
a
i
2 i
di
i x2 1 i
if i 0
dx
a 1 if i
0
P a
6
P( 6 x) x
15
2
2
4
x 1 x
45
8
2 2
2
x 1 x
0.058
5
16
2 3
x 1
0.06
1
2 i 1
c( i)
s ( x) P( i x) d x
1
2
0.04
5
s1( t)
k
s( t) SS ( t)
cc( k) P( k t)
s( t) s1( t)
0
0.02
3.171 10
7
0
1
1
0.5
0
t
0.5
1
1

8.

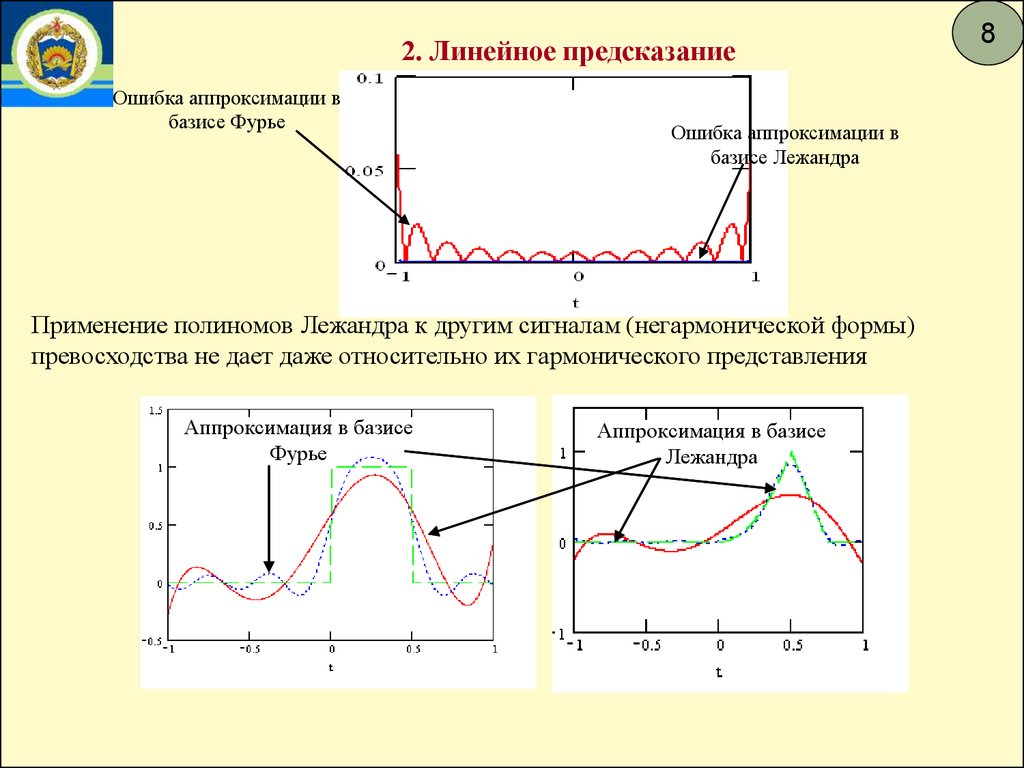
2. Линейное предсказание
Ошибка аппроксимации в
базисе Фурье
Ошибка аппроксимации в
базисе Лежандра
Применение полиномов Лежандра к другим сигналам (негармонической формы)
превосходства не дает даже относительно их гармонического представления
Аппроксимация в базисе
Фурье
Аппроксимация в базисе
Лежандра
8

9.

2. Линейное предсказание
Использование базиса Чебышева
y ( t) sin 3
( t 1)
2
T( n x) cos ( n acos ( x) )
1
T( 0 x) 1
y( t)
T( 1 x) x
0
1
1
0
t
1
9

10.

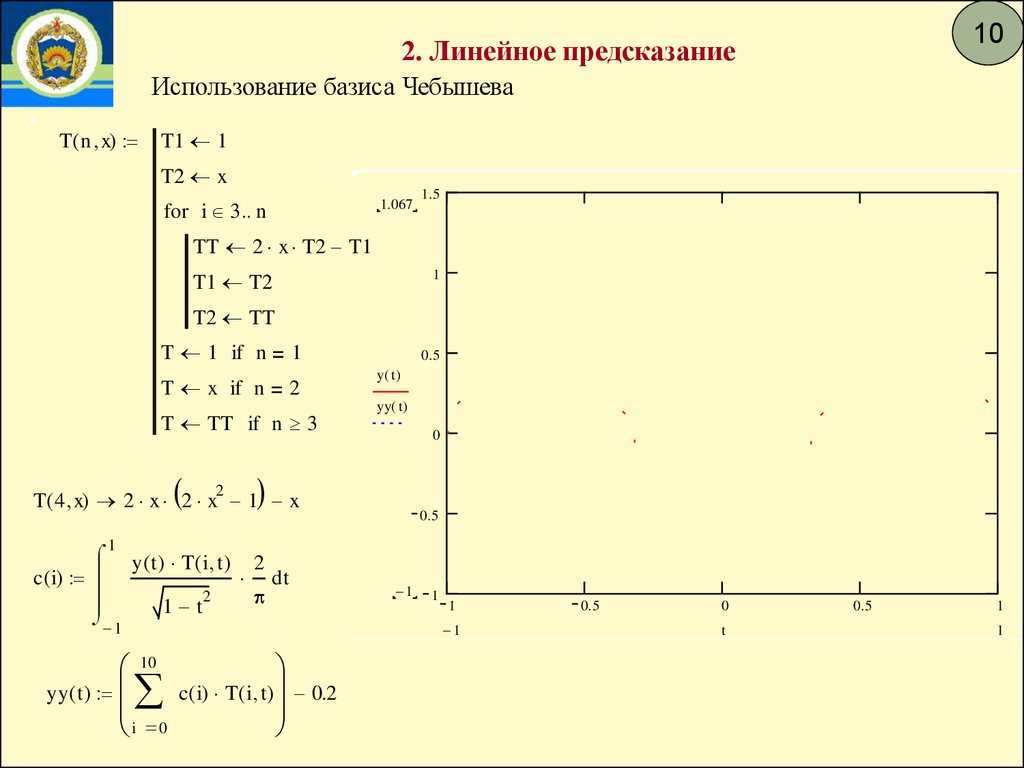
10
2. Линейное предсказание
Использование базиса Чебышева
T( n x)
T1 1
T2 x
for i 3 n
1.067
1.5
TT 2 x T2 T1
T1 T2
1
T2 TT
T 1 if n
T x if n
1
2
T TT if n 3
2
0.5
y( t )
yy( t)
0
T( 4 x) 2 x 2 x 1 x
0.5
1
y ( t ) T( i t ) 2
c( i)
dt
2
1 t
1
10
yy ( t )
c( i) T( i t ) 0.2
i 0
1
1
1
1
0.5
0
t
0.5
1
1

11.

2. Линейное предсказание
11
Однако, при выявлении характеристик гармонических составляющих исследуемых
сигналов разложение по полиномам Лежандра приводит к следующему. Известный
способ анализа таких составляющих, основывающийся на использовании двойного
ортогонального базиса: sin( x) и cos(x) имеет предел по достижимой точности
демодуляции в зависимости от действующего значения отношения мощности сигнала к
спектральной плотности помехи. Сама по себе процедура использования евклидовой
нормы в качестве входного аргумента для демодулятора обуславливает целесообразность
использования n-мерного пространства ортогональных базисов в качестве основы для
представления сигнала при анализе на приемной стороне разложении изменение
приводит к пропорциональному изменению фаз базисных гармоник).
При представлении сигналов на приемной стороне в виде векторов, содержащих
значения мгновенных амплитуд, возможна процедура отыскания приближенных
значений коэффициентов при базисных ортогональных полиномах, участвующих в
разложении исходного сигнала, через решение следующей системы уравнений:
y (t1 ) a1 * f1 (t1 ) a2 * f 2 (t1 ) .. an * f n (t1 ),
y (t ) a * f (t ) a * f (t ) .. a * f (t ),
2
1
1 2
2
2 2
n
n 2
,
...
y (tn ) a1 * f1 (tn ) a2 * f 2 (tn ) .. an * f n (tn ).
где y (t1 ),.. y (tn ) - значения амплитуд сигнала на приемной стороне в моменты времени
t1 ,...tn соответственно, f1 (t ),... f n (t ) значения ортогональных полиномов в
соответствующие значения времени - t , а a1 ,...an - искомые значения коэффициентов.

12.

12
2. Линейное предсказание
Для равной значимости получаемых оценок значений коэффициентов ai ,
необходима их предварительная нормировка. Одним из способов такой нормировки
может служить процедура деления на плечо соответствующего ( k ого) коэффициента:
ak i ak j
wk
(ak max ak min)
Например, для относительной фазовой манипуляции с двумя информационными
сигналами-образами значение евклидова расстояния, без учета ошибки синхронизации и
воздействия помехи, соответствует:
- при несовпадении ( ak i ak j ) образов rj n ,
- при совпадении образов wk 0 .
r1 r1 r 2 r2
r
r
n
при совпадении образов
при несовпадении образов
n
n
r1 r2
Значения Евклидова расстояния для разных ситуаций и их потенциальная разница
разница

13.

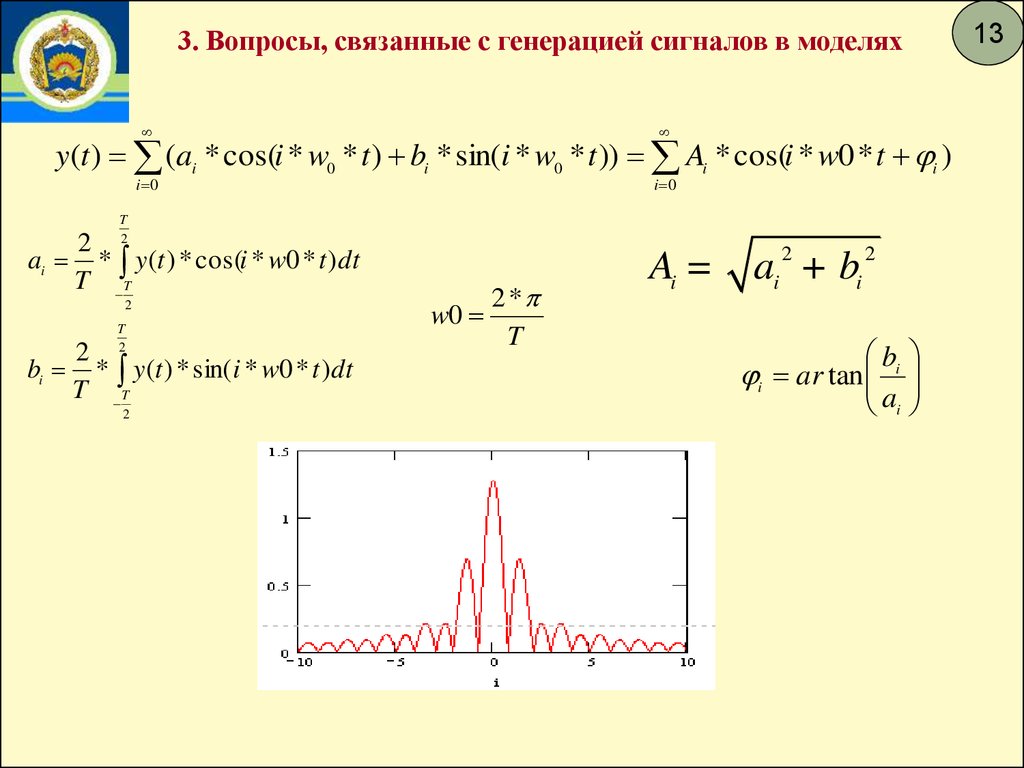
3. Вопросы, связанные с генерацией сигналов в моделях
i 0
i 0
y(t ) (ai * cos(i * w0 * t ) bi * sin(i * w0 * t )) Ai * cos(i * w0 * t i )
ai
T
2
2
* y (t ) * cos(i * w0 * t )dt
T T
2
bi
T
2
2
* y (t ) * sin( i * w0 * t )dt
T T
2
w0
2 *
T
Ai =
ai 2 + bi 2
bi
ai
i ar tan
13

14.

14
3. Вопросы, связанные с генерацией сигналов в моделях
P
Спектральное представление любого сигнала
P
сдвиг начала
интегрирования t
Сигнал U(t)
Спектр сигнала U(t)
f
f
t
1(i )
2(i )
1(i )
2
(i )
2
2
2
2(i )
2

15.

15
4. Методы параметрической оптимизации
Для параметрической оптимизации существует множество расстояний.
Пусть два объекта X и S заданы соответствующими множествами признаков -
x1,..., xn и s1,..., sn .
Тогда расстояние между точками можно определить
как Евклидово расстояние:
как расстояние Минковского:
r( X , S )
n
(x s )
i 1
i
i
2
r( X , S )
,
Расстояние между модулями соответствующих разностей:
n
(
x
s
)
i i
i 1
.
n
r ( X , S ) xi si ,
i 1
которое также не абсолютно в силу следующих обстоятельств:
- во-первых, модуль является неалгебраическим выражением, что делает практически
невозможным решение задачи в функциональном смысле,
- во-вторых, размерность признаков при такой схеме интеграции должна быть одинакова, что
заведомо (при неизвестной природе таких признаков в случае ортогонального разложения)
доказать трудно.
Для ослабления второго ограничения можно использовать либо весовую схему участия
каждой разницы, либо использовать расстояние по Камберру:
n
x s
r( X , S ) i i
i 1 xi si

16.

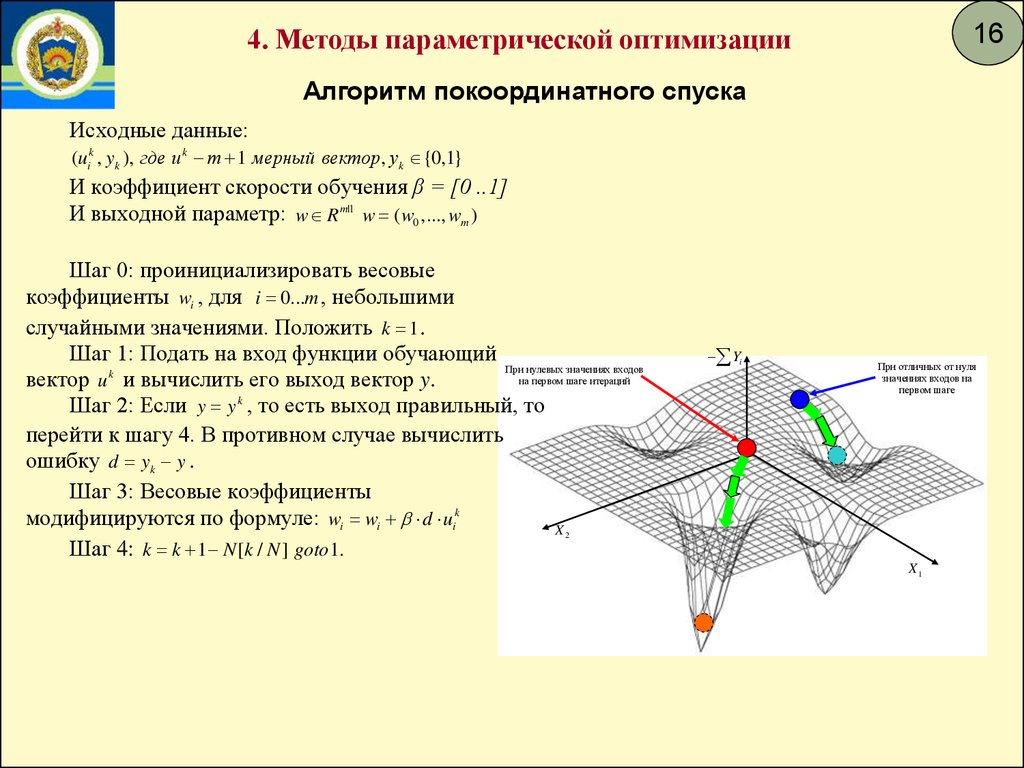
16
4. Методы параметрической оптимизации
Алгоритм покоординатного спуска
Исходные данные:
(uik , yk ), где u k m 1 мерный вектор, yk {0,1}
И коэффициент скорости обучения β = [0 ..1]
И выходной параметр: w R m|1 w ( w0 ,..., wm )
Шаг 0: проинициализировать весовые
коэффициенты wi , для i 0...m , небольшими
случайными значениями. Положить k 1 .
Шаг 1: Подать на вход функции обучающий
При нулевых значениях входов
на первом шаге итераций
вектор u k и вычислить его выход вектор y.
Шаг 2: Если y y k , то есть выход правильный, то
перейти к шагу 4. В противном случае вычислить
ошибку d yk y .
Шаг 3: Весовые коэффициенты
модифицируются по формуле: wi wi d uik
X
Шаг 4: k k 1 N [k / N ] goto 1.
Yi
При отличных от нуля
значениях входов на
первом шаге
2
X1