Similar presentations:
Фазовые равновесия в двухкомпонентных системах: зависимость растворимости вещества от температуры, криоскопия, эбулиоскопия
1.
Лекция 12Фазовые равновесия в двухкомпонентных
системах:зависимость растворимости вещества от
температуры,криоскопия, эбулиоскопия,
экстракционное равновесие. Коллигативные
свойства. Осмос. Уравнение Вант-Гоффа.
2.
Лекция 11Термодинамическая классификация и модели
растворов.
Мольная энергия Гиббса смешения. Идеальные
растворы. Закон Рауля. Закон Генри.
Стандартный химический потенциал компонента в
жидком и твердом растворах. Стандартные
состояния "чистое вещество" и "бесконечноразбавленный раствор". Неидеальные растворы.
Метод активностей Льюиса. Вычисление
коэффициентов активности из экспериментальных
данных по давлению пара компонентов раствора.
3.
Фазовые равновесия в двухкомпонентных системах4.
2 баллХимический потенциал компонента в жидком и твердом
растворах обладает следующими свойствами (отметьте
правильные утверждения):
1) Зависит от внешнего давления на раствор.
2) Не зависит от внешнего давления на раствор.
3) Меньше или равен химическому потенциалу чистого
компонента.
4) При постоянных температуре и давлении линейно зависит
от ln x, где х – мольная доля компонента.
5) Связан с химическим потенциалом второго компонента
уравнением Гиббса-Дюгема.
5.
Свойства идеального раствора двух компонентов.2 балл
Отметьте правильные утверждения:
1) Активность компонента в идеальном растворе равна
мольной доле.
2) Энтропия смешения идеального раствора меньше нуля.
3) Энергия Гиббса смешения идеального раствора меньше
нуля.
4) Химический потенциал любого компонента выражается
формулой μ = μ0 + RT ln x при x 1.
5) Если пар - идеальный газ, активность компонента в
идеальном растворе равна: a = p/p0, где р0 = 1 бар.
6.
ФазаГаз:
Ид.
Реал.
p
(T ) RT ln 0
p
f
0
(T ) RT ln 0
p
Жд.,тв.:
Ид.
(T , p) RT ln x
0
0
Реал.
0 (T , p) RT ln a
Жд.,тв.:
Раз. р-р.
(T , p) RT ln x
(T , p ) RT ln a
Растворитель !
,
0
0 (ид.,T , p0 1бар)
0
0
0
S ;
0
T p
p T
0 ( T , p, x 1)
0
0
0
0
S
;
V
T
p
p
T
( T , p) lim RT ln x
x 0
S
;
V
T
p
p
T
7.
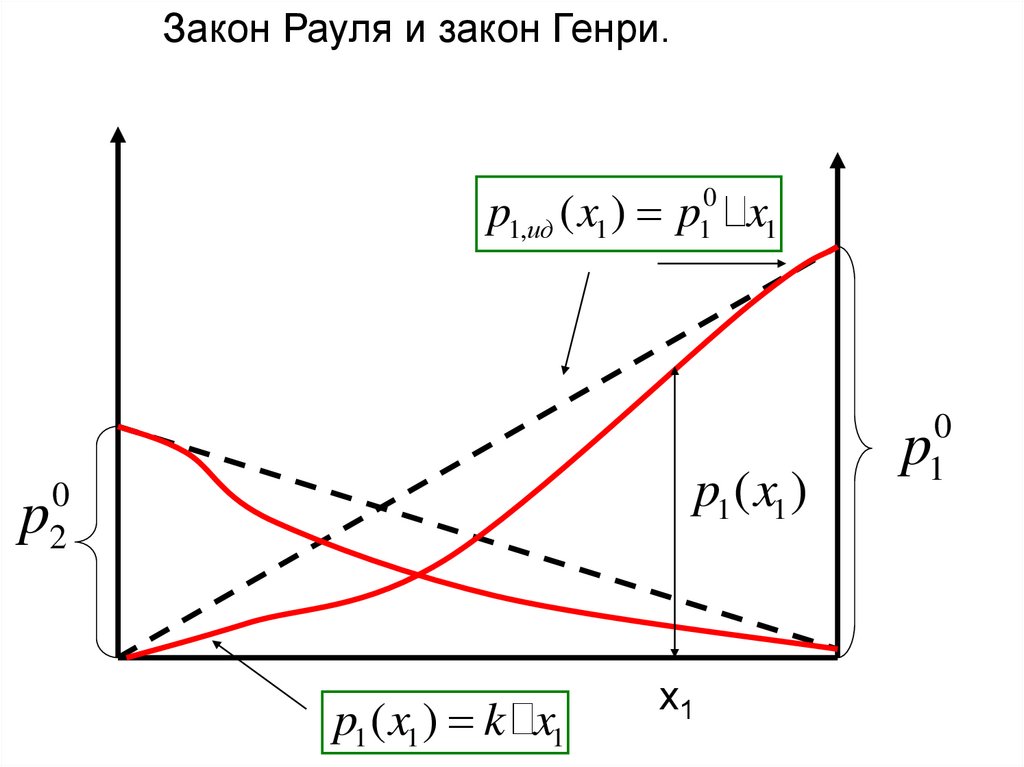
Закон Рауля и закон Генри.p1,ид ( x1 ) p10 x1
p1 ( x1 )
0
2
p
p1 ( x1 ) k x1
x1
0
1
p
8.
Коллигативные свойстваРавновесия с участием компонента идеального раствора:
i RT ln xi ; xi 1
0
i
9.
Растворимость тв. вещества как функция температурыФаза (1) –ч. тв.
Фаза (2) - раствор.
Для фазы (2) выполняется закон Рауля.
1(1) 10,(1) 1(2) 10,(2) RT ln x1(2) ; T (1) T ( 2) ; p (1) p ( 2)
x1(2)
?
T p
10,(2) 10,(1)
(2)
R
ln
x
1
T
Gплавл
T
T
ln x1(2)
H плавл
R
2
T
T
р
р
ln x1(2)
H плавл
2
T
RT
р
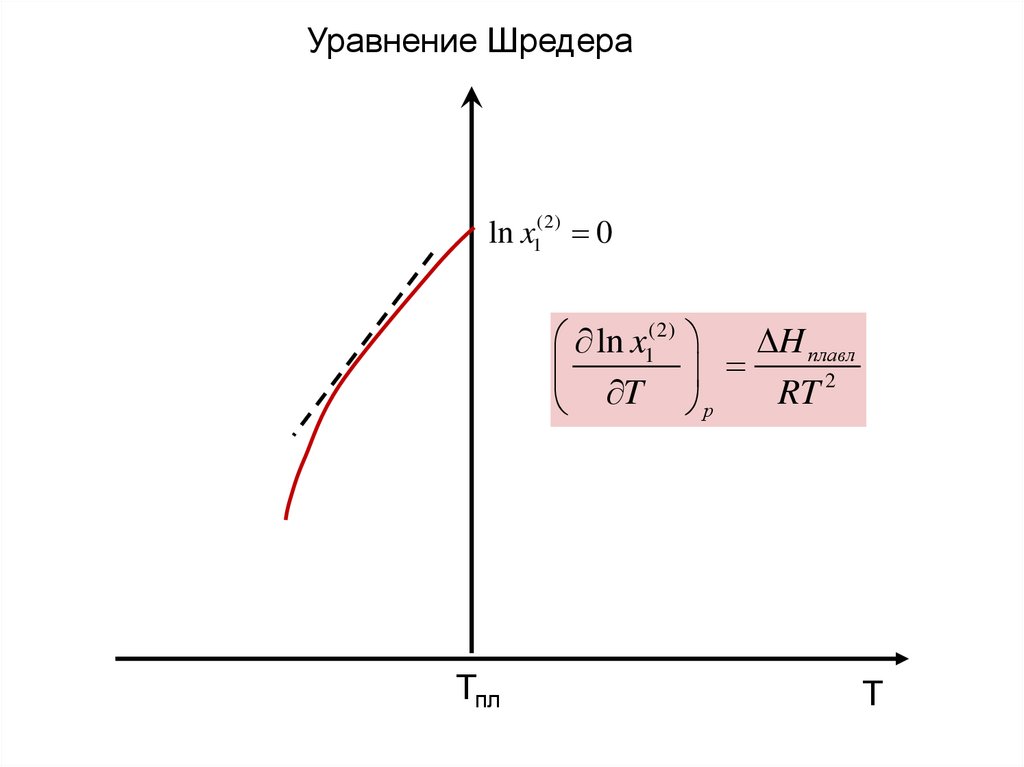
10.
Уравнение Шредераln x1(2) 0
ln x1(2)
H плавл
2
T
RT
р
Тпл
Т
11.
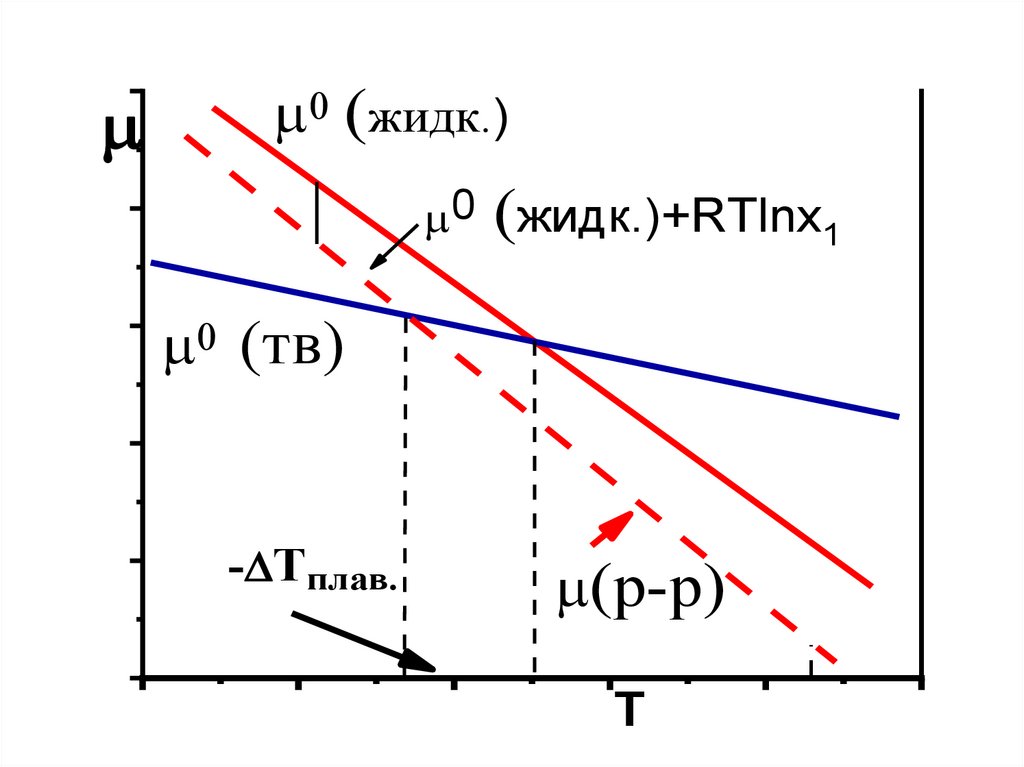
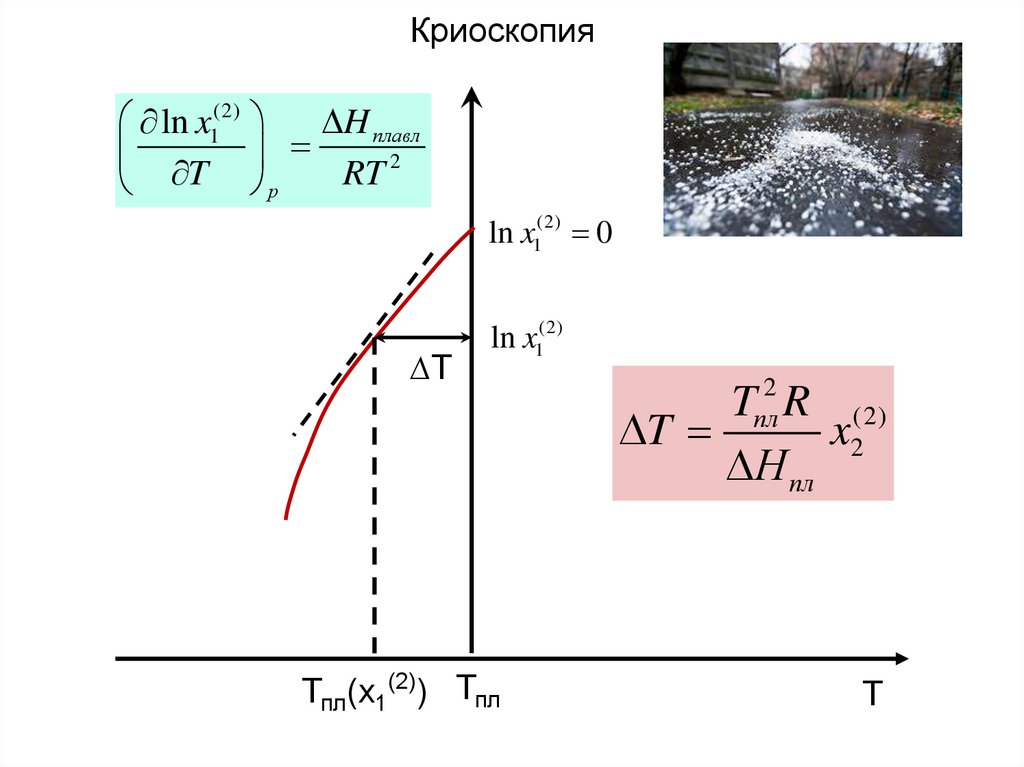
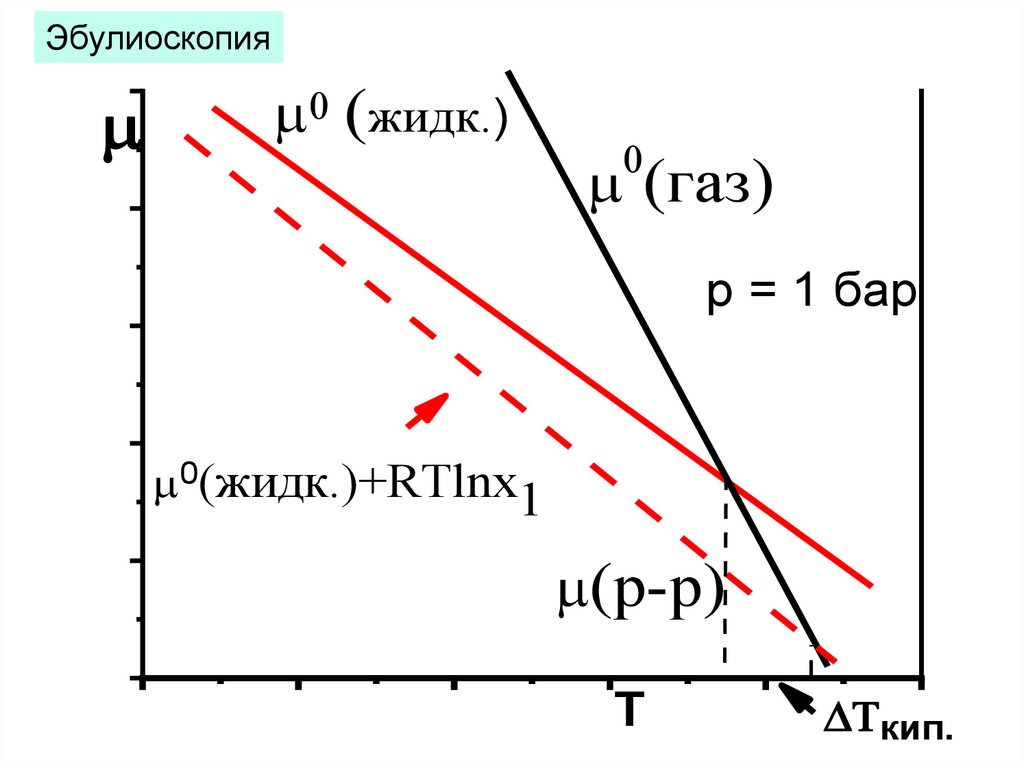
Криоскопия, эбулиоскопия12.
0 (жидк.)0 (жидк.)+RTlnx1
0 (тв)
- Tплав.
(р-р)
T
13.
Криоскопия.Фаза (1) –ч. тв.
Фаза (2) – ч.жд. или раствор.
Для фазы (2) выполняется закон Рауля.
T Tпл ( x1 1) Tпл ( x1(2) )
1(1) 10,(1) 1(2) 10,(2) ; T Tпл x1 1 Tпл
1(1) 10,(1) 1(2) 10,(2) RT ln x1(2) ; T Tпл ( х1(2) )
ln x1(2)
H плавл
2
T
RT
р
Tпл2 R (2)
T
x2
Н пл
х1
d ln x
1
1
Т пл ( х1 )
Tпл
H пл
H пл Tпл Tпл ( х1(2) )
(2)
dT ; ln x1
RТ 2
R Tпл Tпл ( х1(2) )
ln x1(2) ln(1 x2(2) ) x2(2) ; Tпл2 Tпл Tпл ( x1 )
14.
Криоскопияln x1(2)
H плавл
2
T
RT
р
ln x1(2) 0
∆Т
ln x1(2)
Тпл(х1(2)) Тпл
2
пл
T R (2)
T
x2
Н пл
Т
15.
Эбулиоскопия0 (жидк.)
0
(газ)
p = 1 бар
0(жидк.)+RTlnx1
(р-р)
T
Tкип.
16.
Эбулиоскопия.Фаза (2) –ч.жд. или раствор
Фаза (1) – пар, р=1бар.
Для фазы (2) выполняется закон Рауля.
T Tкип ( x1(2) ) Tкип ( x1 1)
0
p
10,(1) RT ln 0 10,(1) 1(2) 10,(2) ; T Tкип x1 1 Tкип
p
0
p
10,(1) RT ln 0 10,(1) 1(2) 10,(2) RT ln x1(2) ; T Tкип ( х1 )
p
2
Tкип
R (2)
T
x2
Н кип
ln x1(2) ln(1 x2(2) ) x2(2) ; Tпл2 Tпл Tпл ( x1 )
17.
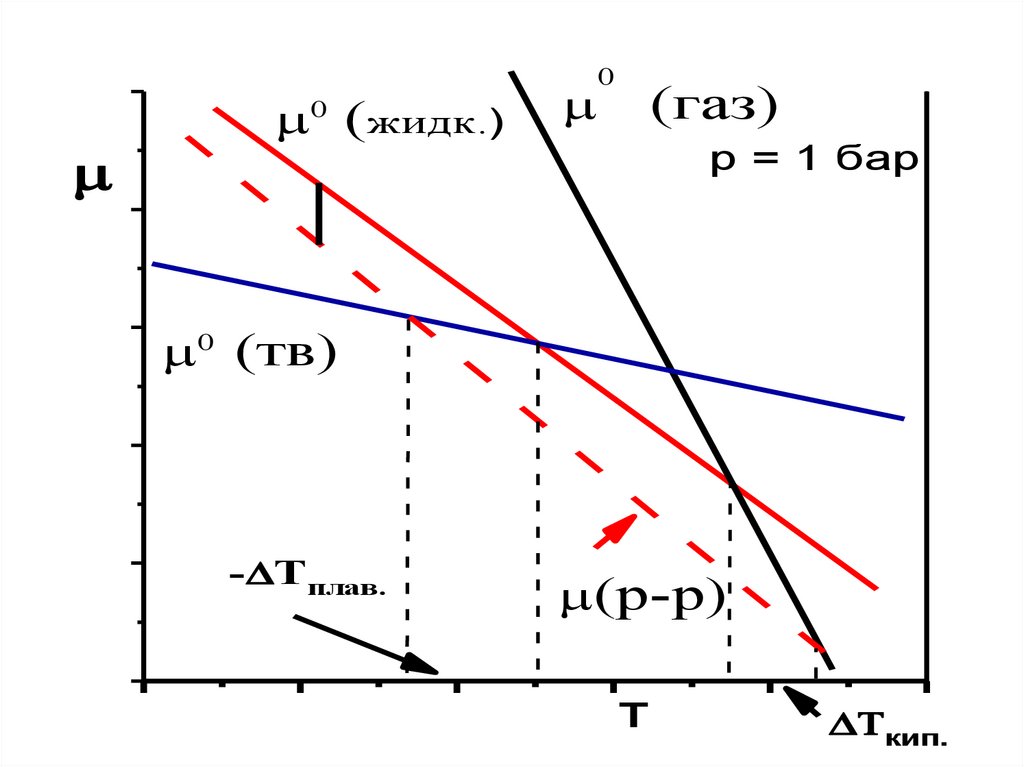
0 (жидк.)0
(газ)
p = 1 бар
0 (тв)
- Tплав.
(р-р)
T
Tкип.
18.
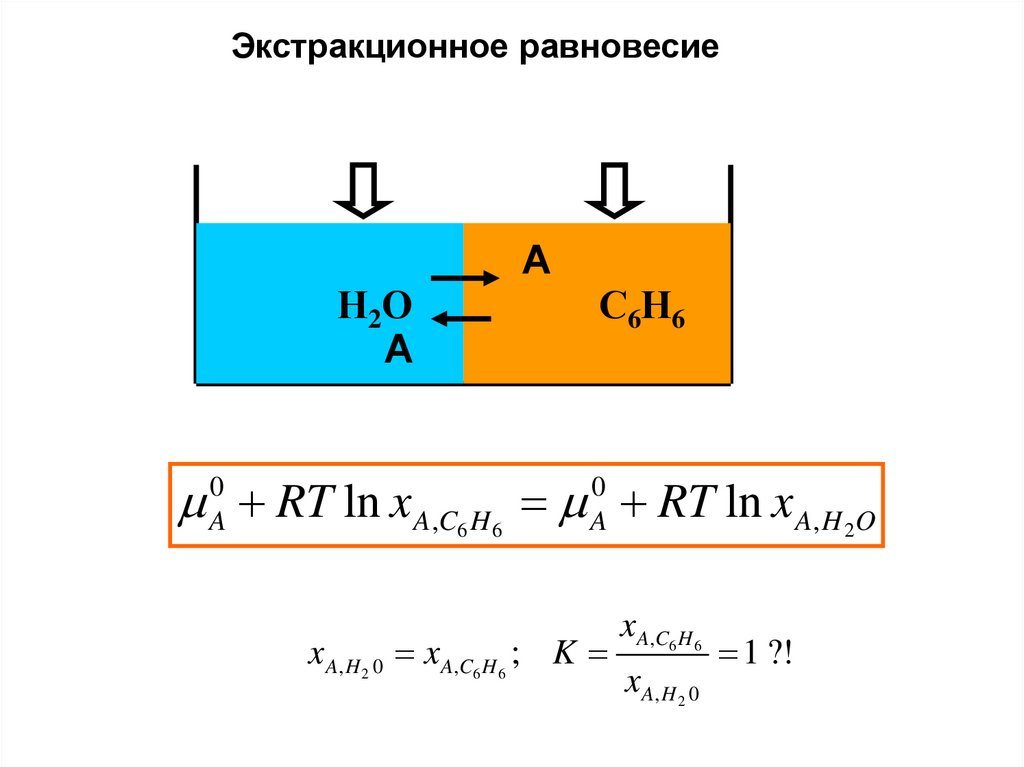
Экстракционное равновесиеА
С6Н6 С Н
6 6
Н2О
А
A0 RT ln x A,C H A0 RT ln x A, H O
6
6
x A, H 2 0 x A,C6 H 6 ; K
2
x A,C6 H 6
x A, H 2 0
1 ?!
19.
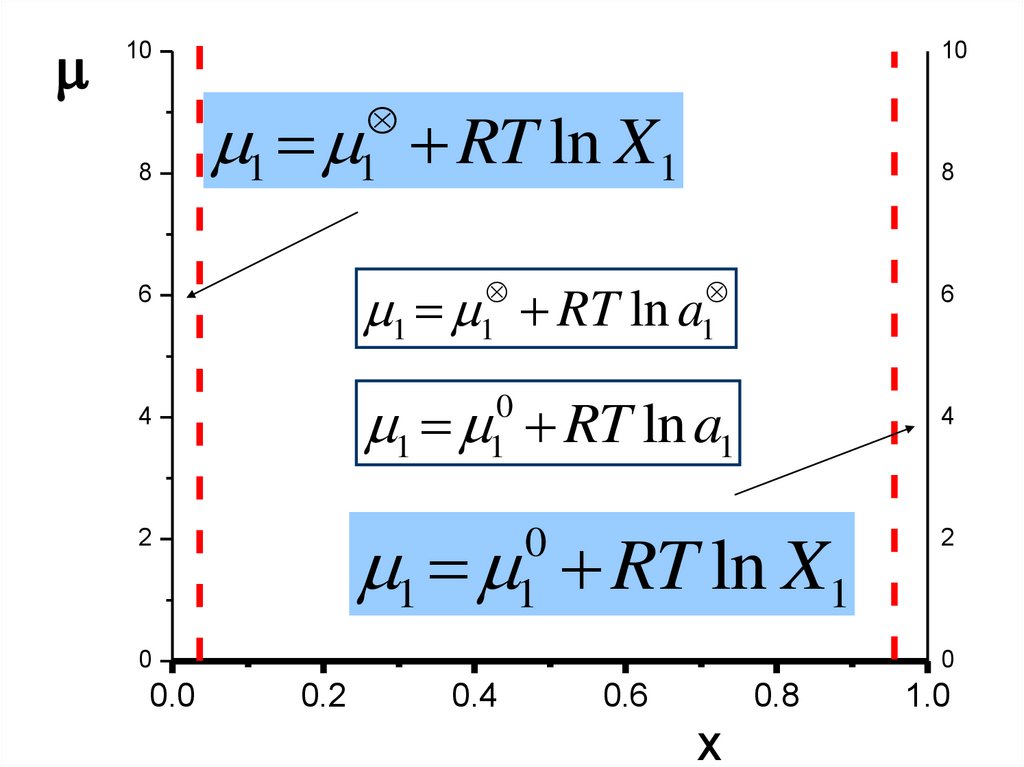
108
10
1 RT ln X1
1
8
1 RT ln a
1
6
1
6
1 RT ln a1
0
1
4
4
1 RT ln X1
0
1
2
0
0.0
2
0
0.2
0.4
0.6
0.8
X
1.0
20.
Экстракционное равновесиеН2О
А
A,C6 H6
G
А
С6Н6 С Н
6 6
RT ln xA,C6 H6
A, H 2 0
A,C6 H 6
RT ln
A, H 2 O
x A,C6 H 6
x A, H 2 0
RT ln xA, H2O
; K
x A,C6 H 6
x A, H 2 0
e
G
RT
21.
Мембранное равновесие. Осмос.P
xH2O
xA
H2O
H2O
P+P
A
0
H 2O
(T , p)
0
H 2O
(T , p P) RT ln xH2O
22.
ФазаГаз:
Ид.
Реал.
p
(T ) RT ln 0
p
f
0
(T ) RT ln 0
p
Жд.,тв.:
Ид.
(T , p) RT ln x
0
0
Реал.
0 (T , p) RT ln a
Жд.,тв.:
Раз. р-р.
(T , p) RT ln x
(T , p ) RT ln a
Растворитель !
,
0
0 (ид.,T , p0 1бар)
0
0
0
S ;
0
T p
p T
0 ( T , p, x 1)
0
0
0
0
S
;
V
T
p
p
T
( T , p) lim RT ln x
x 0
S
;
V
T
p
p
T
23.
Уравнение Вант-Гоффа0
H 2O
(T , p)
0
H 2O
(T , p P) RT ln xH2O
p P
0
H 2O
(T , p )
0
H 2O
Vdp RT ln x
(T , p )
H 2O
p
p P
Vdp V p P p V
0
0
P RT ln xH 2O
p
V 0P
ln xH 2O ln 1 x A x A
RT
x A RT
P
0
V
24.
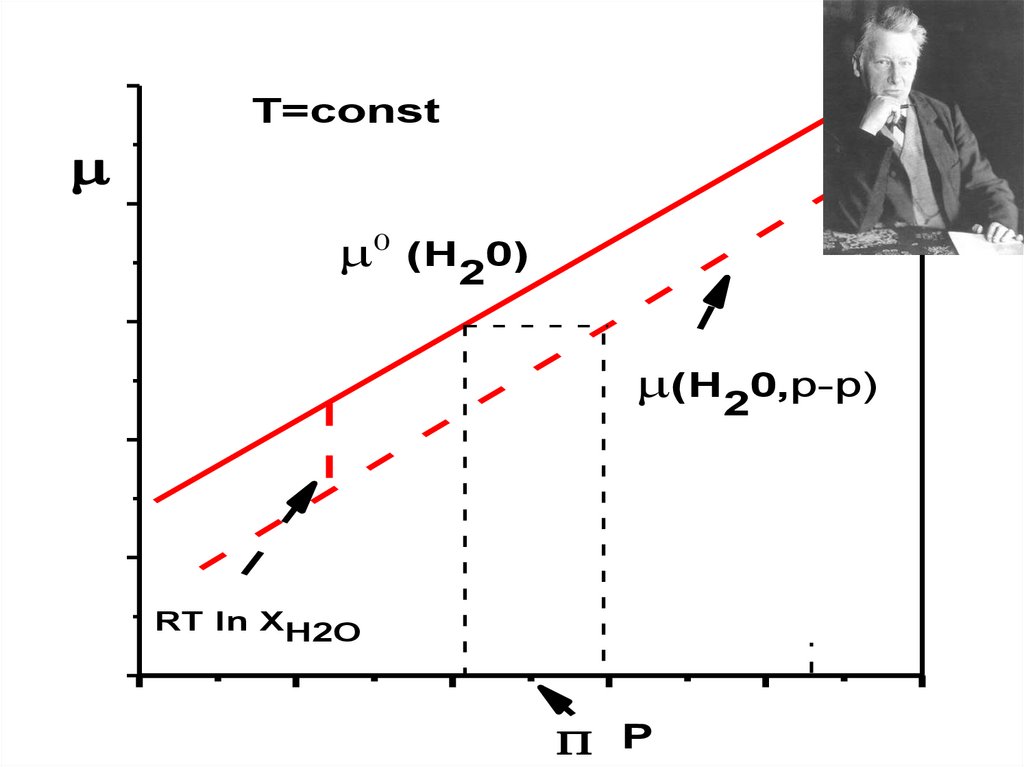
T=const0
(H 0)
2
(H20,р-р)
RT ln XH2O
P P
25.
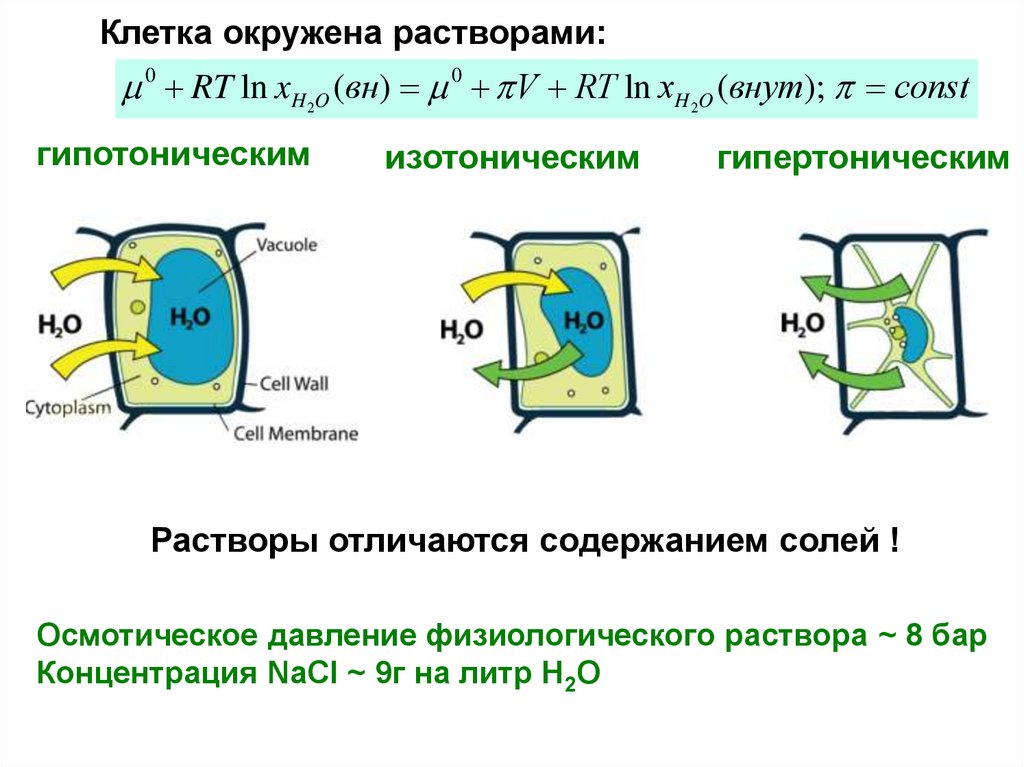
Клетка окружена растворами:0 RT ln xH O (вн) 0 V RT ln xH O (внут); const
2
гипотоническим
2
изотоническим
гипертоническим
Растворы отличаются содержанием солей !
Осмотическое давление физиологического раствора ~ 8 бар
Концентрация NaCl ~ 9г на литр Н2О
26.
Рыба в осмотическом равновесии0 RT ln xH O (вн) 0 V RT ln xH O (внут); const
2
В слишком чистой воде.
Требуется большое π
2
В слишком соленой воде.
Требуется маленькое π
27.
ОсмосP
P
P
H2O+A
H2O
H2O+A
H2O
28.
Диаграммы p – х и Т-х в двухкомпонентнойсистеме
29.
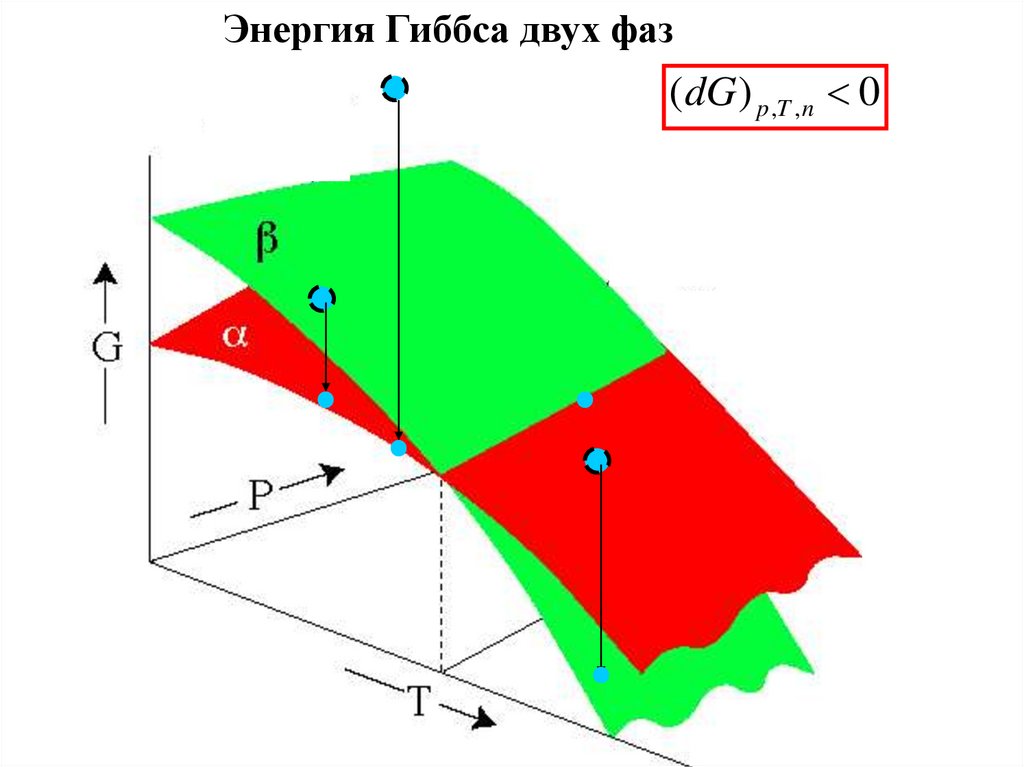
Энергия Гиббса двух фаз(dG ) p ,T ,n 0
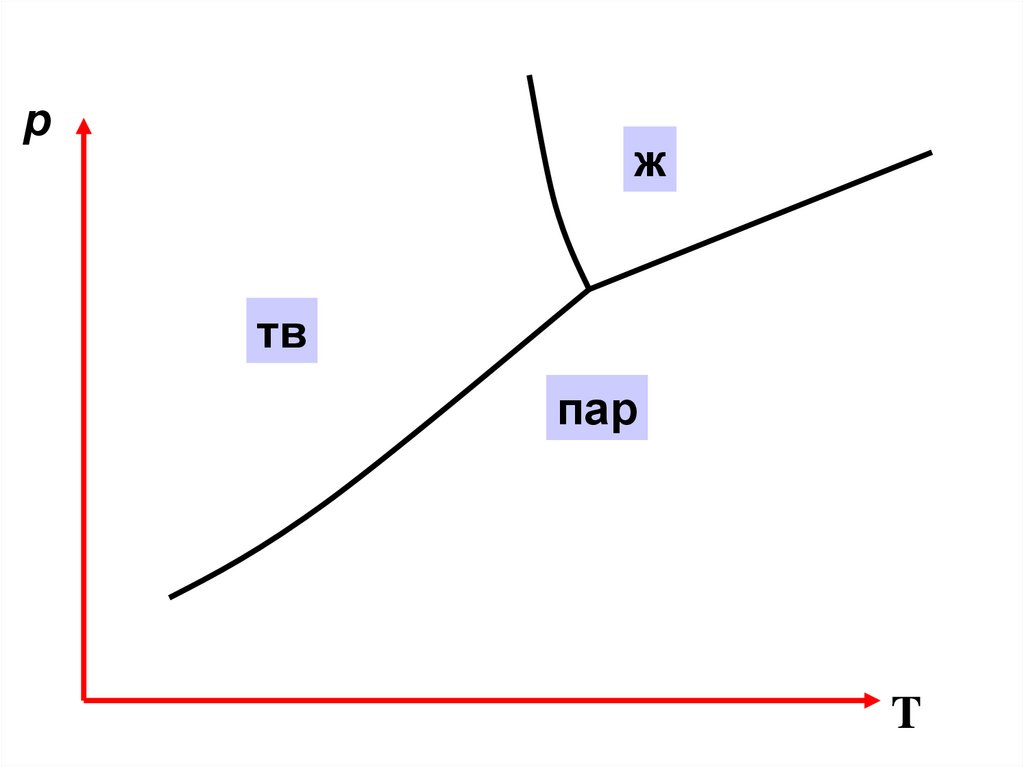
30.
pж
тв
α
пар
β
T
31.
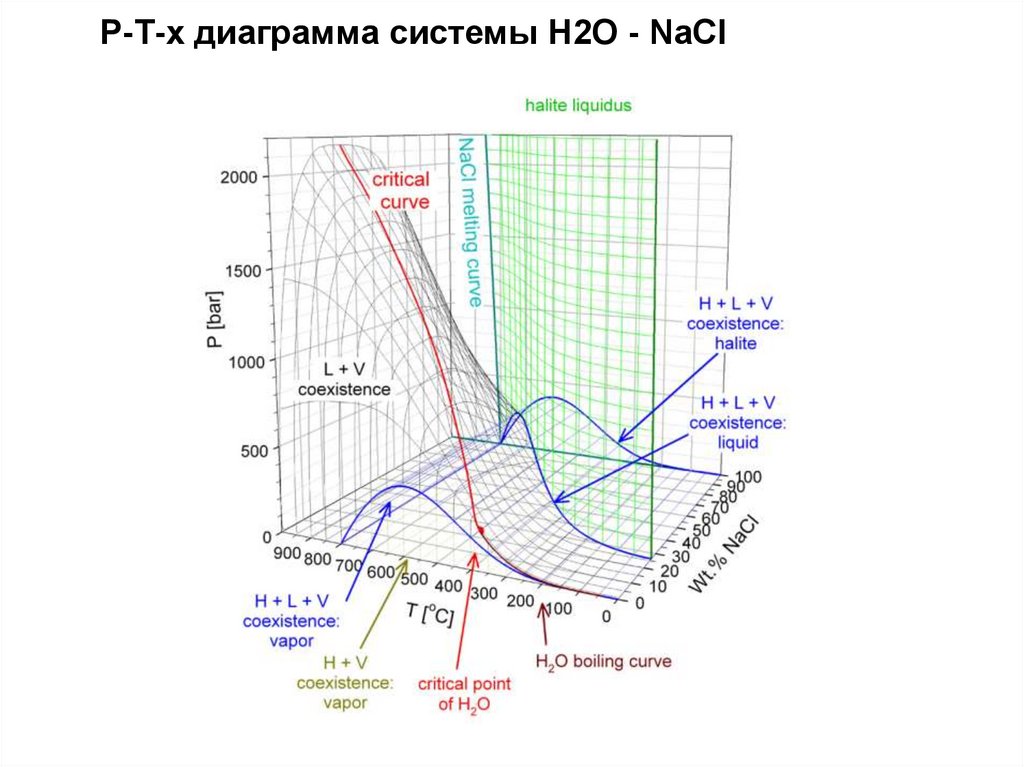
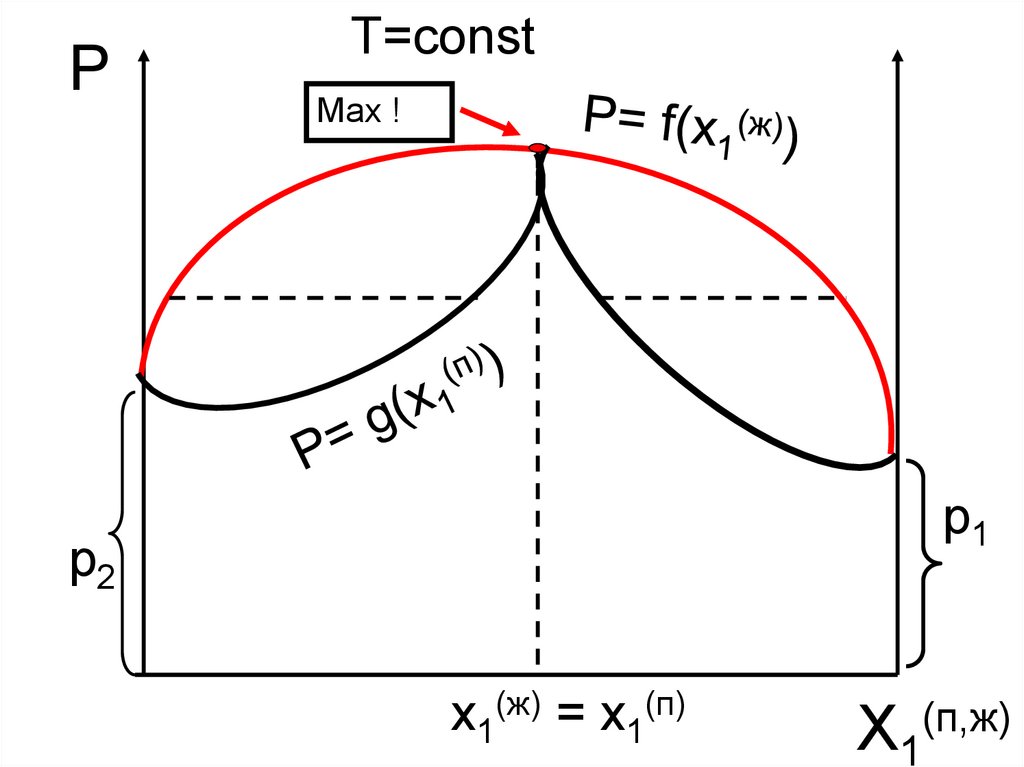
Р-Т-х диаграмма системы Н2О - NaCl32.
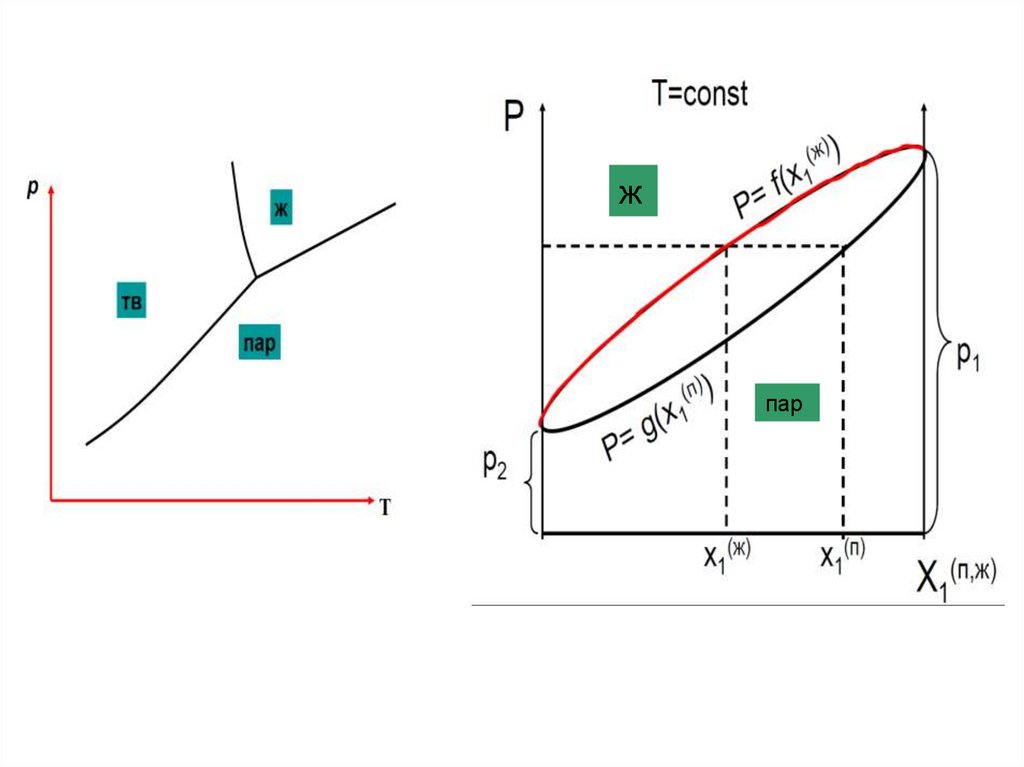
PT=const
p1
p2
x1(ж)
x1(п)
X1(п,ж)
33.
жпар
34.
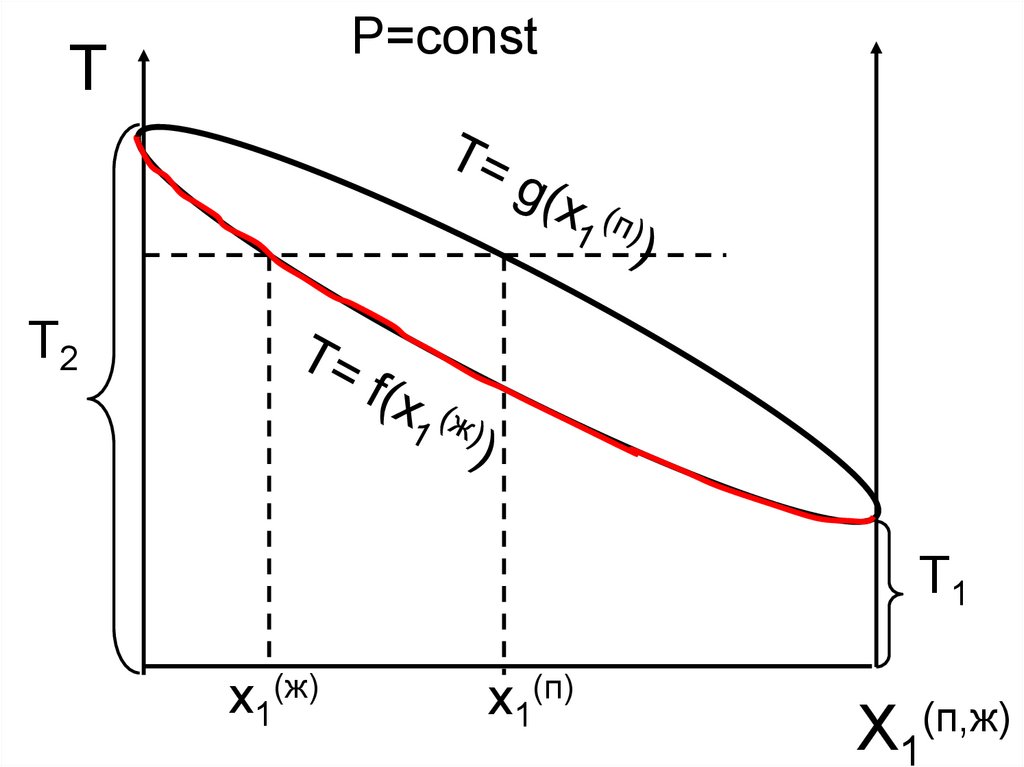
P=constT
T2
T1
x1(ж)
x1(п)
X1(п,ж)
35.
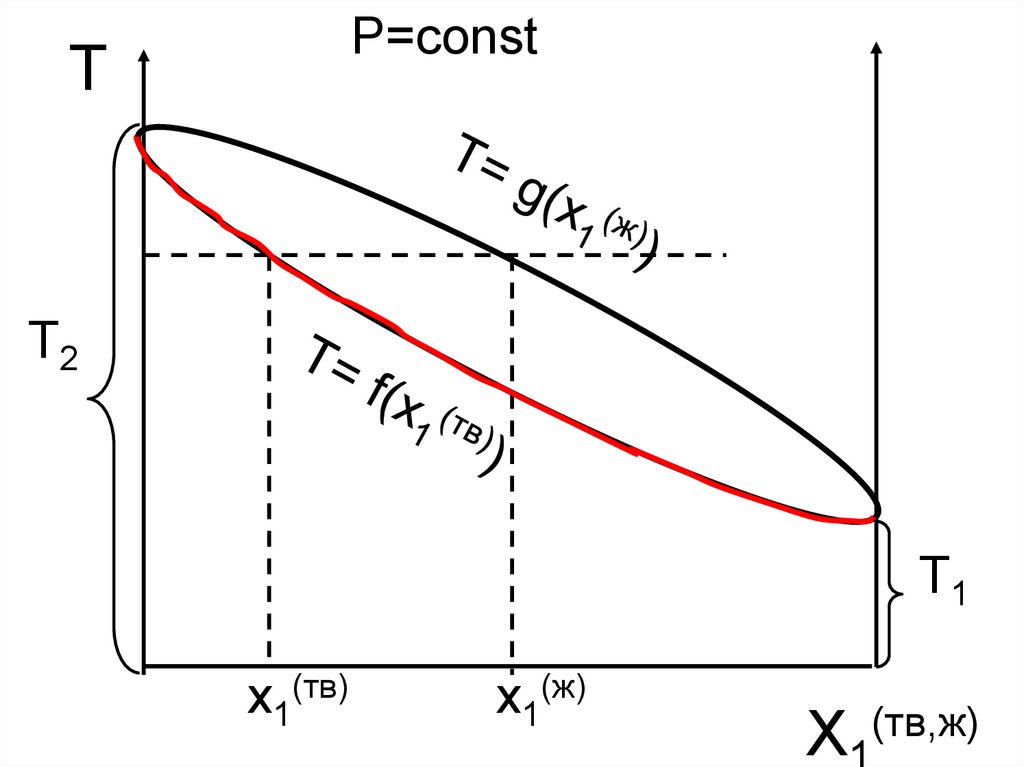
P=constT
T2
T1
x1(тв)
x1(ж)
X
(тв,ж)
36.
Равновесие твердый р-р – жидкий р-рp=const
37.
PT=const
Max !
p1
p2
x1(ж) = x1(п)
X1(п,ж)
38.
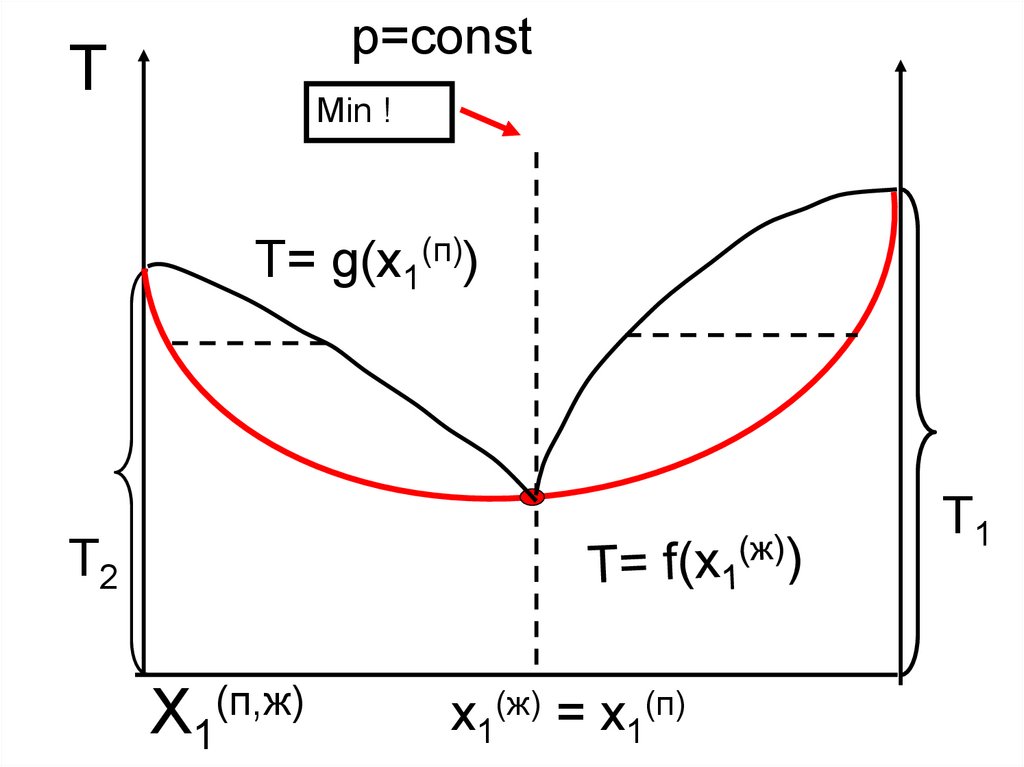
р=constТ
Min !
T= g(x1(п))
Т1
Т2
X1(п,ж)
x1(ж) = x1(п)
39.
УРАВНЕНИЕ ГИББСА-ДЮГЕМА.dU TdS pdV 1dni
i
n
U TS pV i ni
1
dU TdS SdT pdV Vdp i dni ni d i
i
i
SdT Vdp ni d i 0;
i
p, T const ,
n d
i
i
i
0





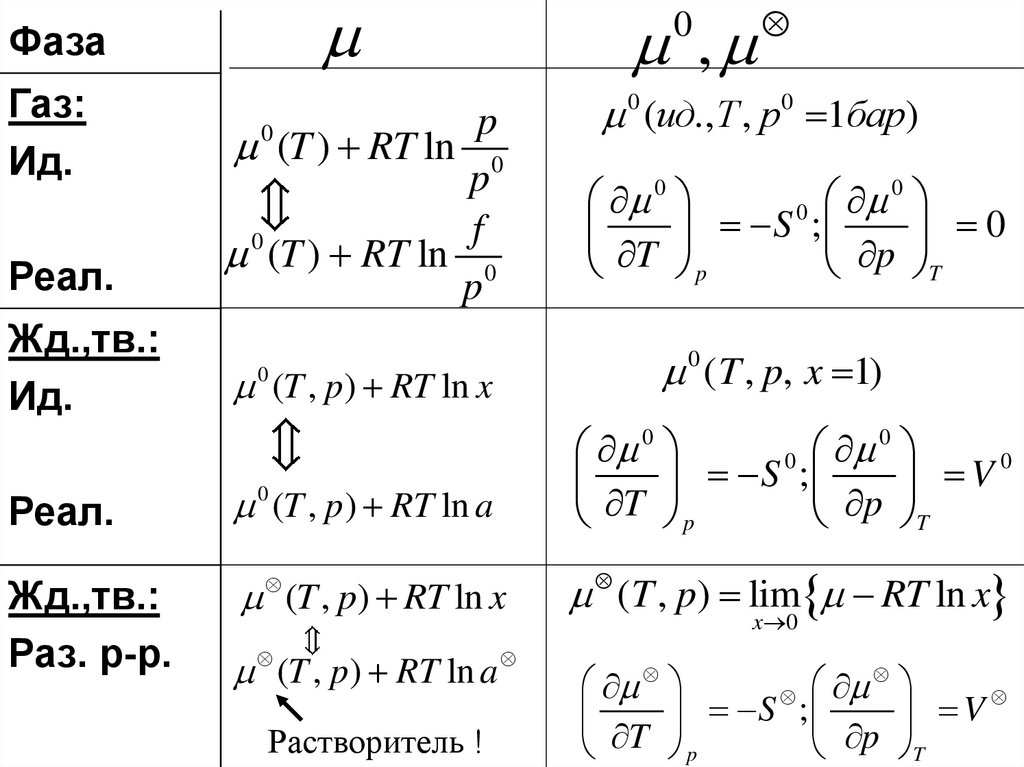







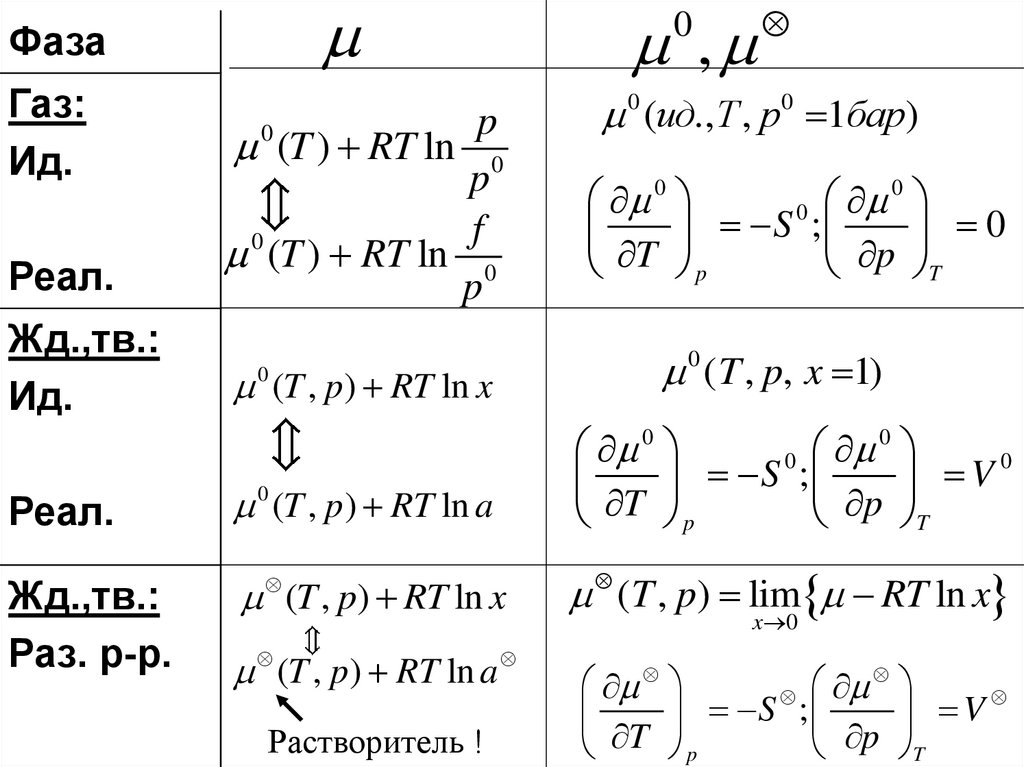







 chemistry
chemistry








