Тригонометрические функции

1.

2.

Повторение. Схема исследования функции
При исследовании функции находят:
1) Область определения
Область значений
2) Четность, периодичность,
непрерывность
3) Нули функции
4) Промежутки знакопостоянства
5) Промежутки возрастания, убывания
6) Экстремумы

3.

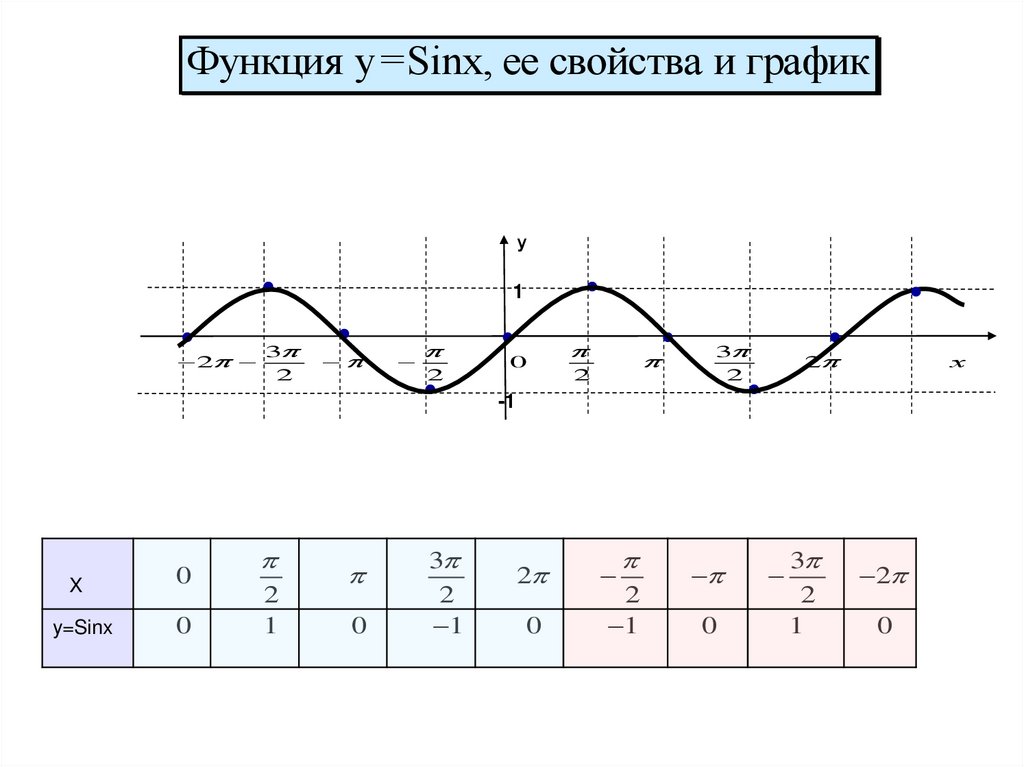
Функция y=Sinx, ее свойства и график
у
1
2
3
2
2
0
2
3
2
2
х
-1
Xx
0
y
y=Sinx
0
2
1
0
3
2
1
2
0
2
1
0
3
2
1
2
0

4.

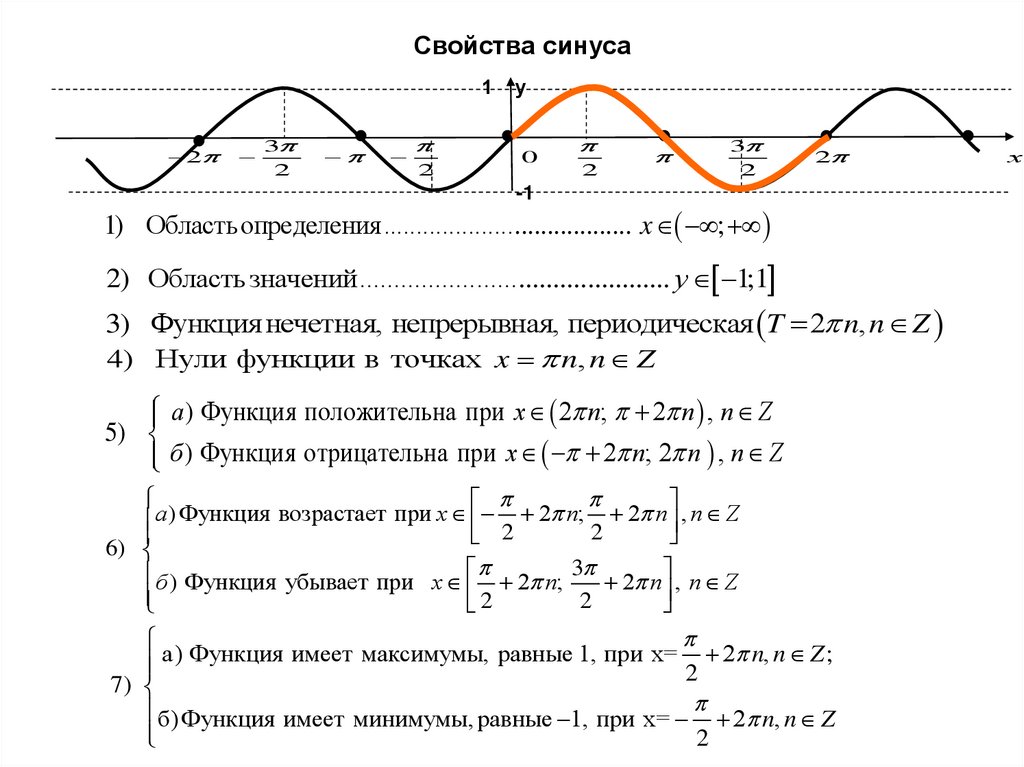
Свойства синуса
1
2
3
2
2
у
0
2
3
2
2
-1
1) Областьопределения...................................... x ;
2) Область значений............................................. у 1;1
3) Функция нечетная, непрерывная, периодическая T 2 n, n Z
4) Нули функции в точках x n, n Z
а) Функция положительна при x 2 n; 2 n , n Z
5)
б ) Функция отрицательна при x 2 n; 2 n , n Z
а
)
Функция
возрастает
при
x
2
n
;
2
n
,n Z
2
2
6)
б ) Функция убывает при x 2 n; 3 2 n , n Z
2
2
а)
Функция
имеет
максимумы,
равные
1,
при
x=
2 n, n Z ;
2
7)
б) Функция имеет минимумы, равные 1, при x= 2 n, n Z
2
х

5.

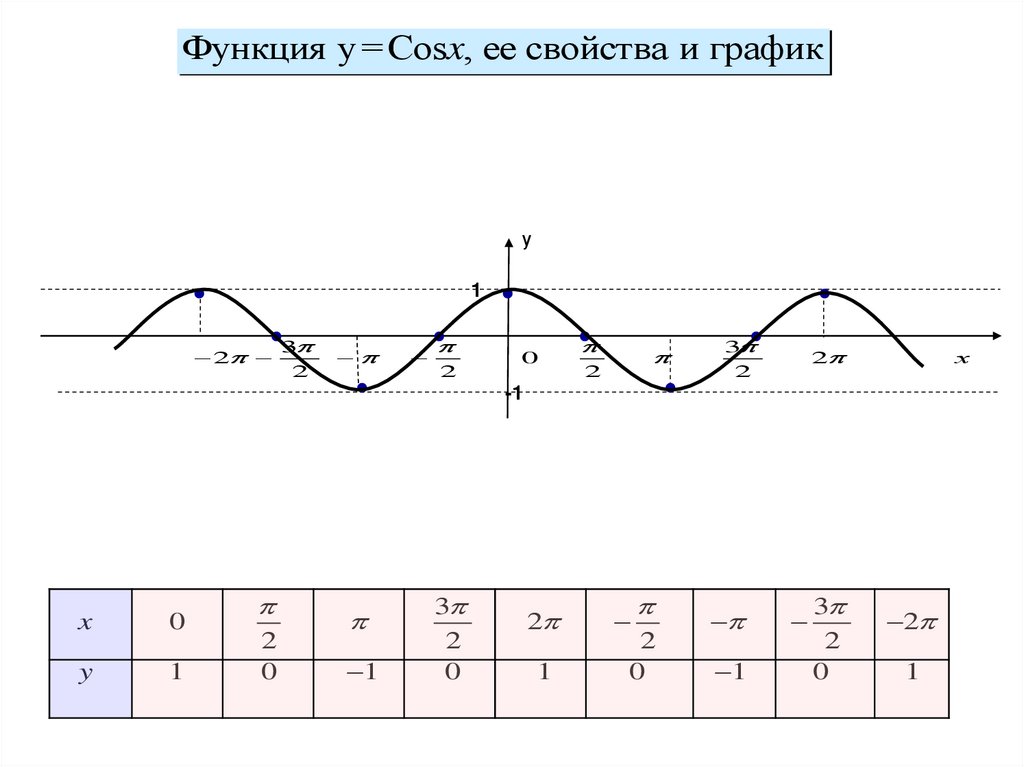
Функция y=Cosx, ее свойства и график
у
1
2
3
2
2
0
2
3
2
2
х
-1
x
0
y
1
2
0
1
3
2
0
2
1
2
0
1
3
2
0
2
1

6.

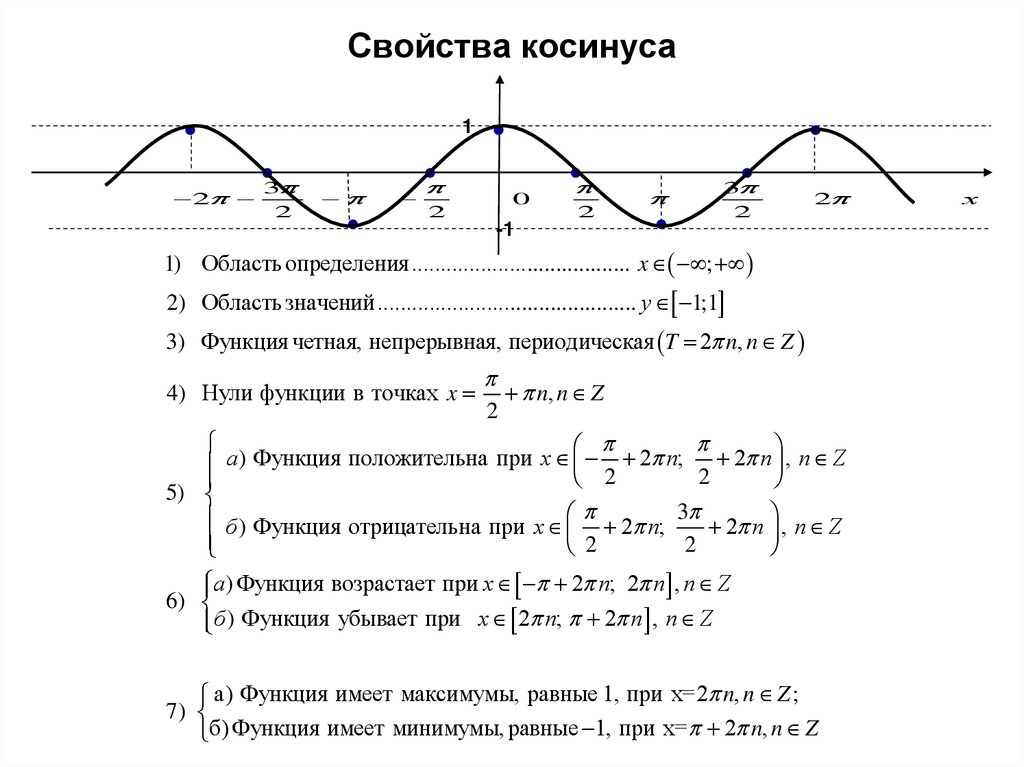
Свойства косинуса
1
2
3
2
0
2
2
3
2
2
-1
1) Область определения...................................... x ;
2) Область значений............................................. у 1;1
3) Функция четная, непрерывная, периодическая T 2 n, n Z
4) Нули функции в точках x
2
n, n Z
а
)
Функция
положительна
при
x
2
n
;
2
n
, n Z
2
2
5)
б ) Функция отрицательна при x 2 n; 3 2 n , n Z
2
2
а ) Функция возрастает при x 2 n; 2 n , n Z
6)
б ) Функция убывает при x 2 n; 2 n , n Z
а) Функция имеет максимумы, равные 1, при x=2 n, n Z ;
7)
б) Функция имеет минимумы, равные 1, при x= 2 n, n Z
х

7.

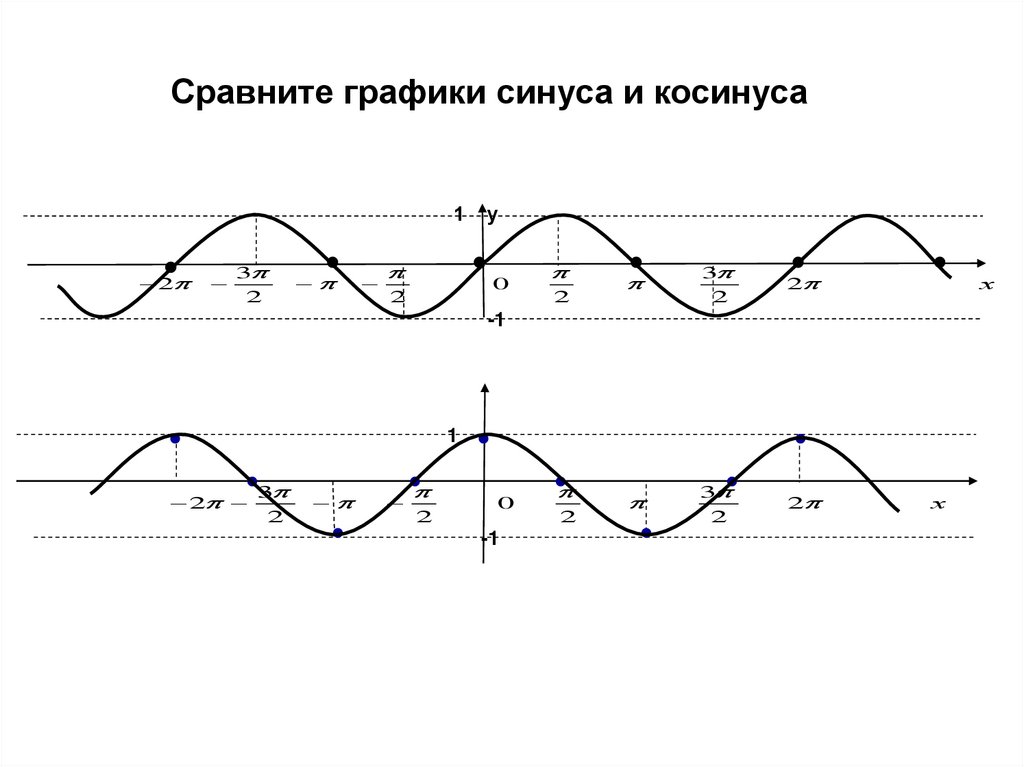
Сравните графики синуса и косинуса
1
2
3
2
у
0
2
2
3
2
2
3
2
2
х
-1
1
2
3
2
2
0
-1
2
х

8.

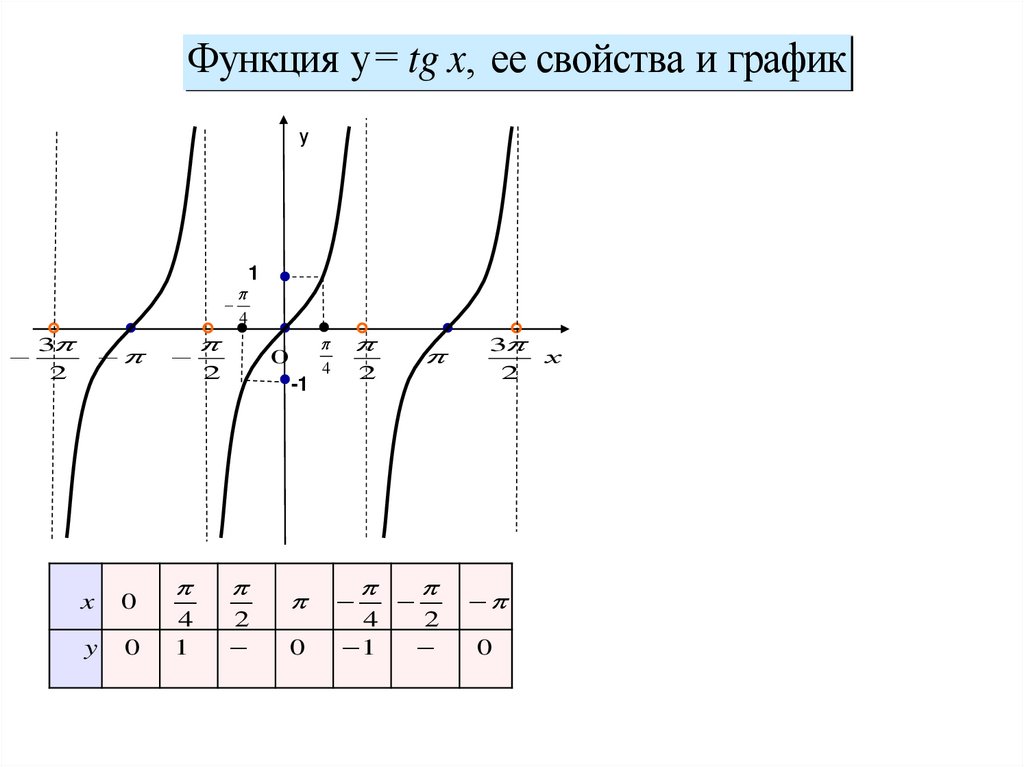
Функция y= tg x, ее свойства и график
у
3
2
x
0
y
0
1
4
0
2
-1
4
1
2
0
4
2
4
1
2
3
2
0
х

9.

Свойства тангенса
1) Область определения x - n; n
2
2
2) Область значений y ;
у
,n Z
3) Нечетная, периодическая T n , n Z
1
3
2
2
4) Нули функции в точках x = n, n Z
4
0
-1
4
2
Функция
положительна
при
x
n
;
n
, n Z
2
5)
Функция отрицательна при x n; n , n Z
2
6) Функция возрастает при x n;
n , n Z
2
2
7) Экстремумов не имеет
3
х
2

10.

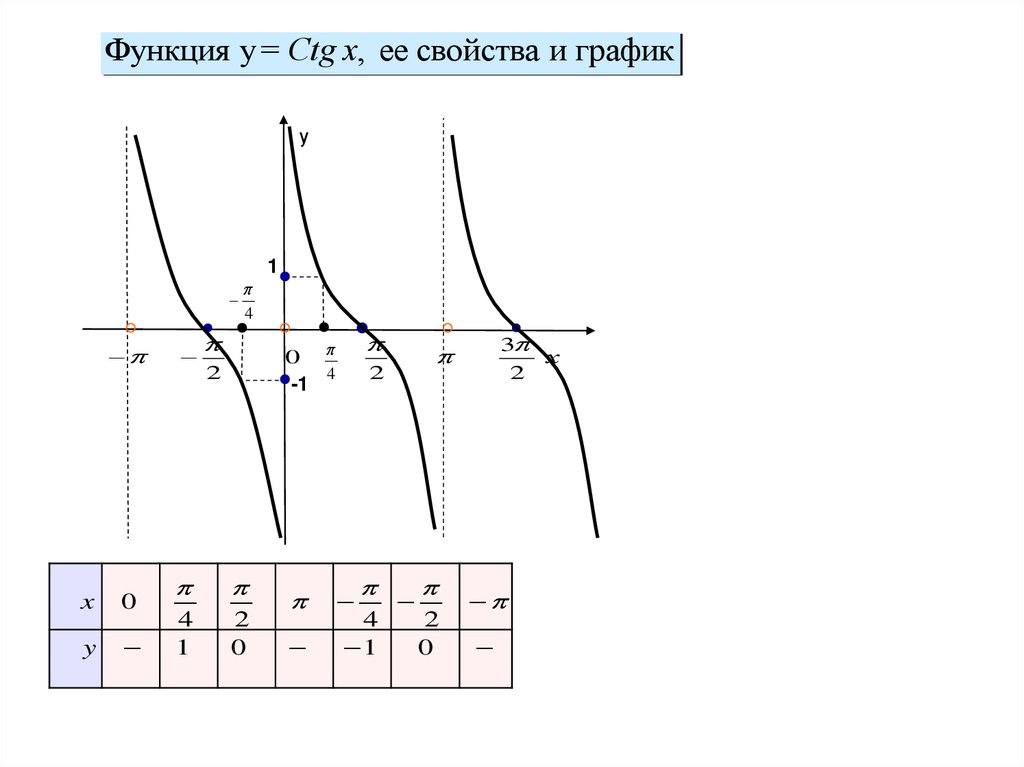
Функция y= Сtg x, ее свойства и график
у
x
0
y
1
4
0
4
-1
2
4
1
2
0
2
4
1
3
х
2
2
0

11.

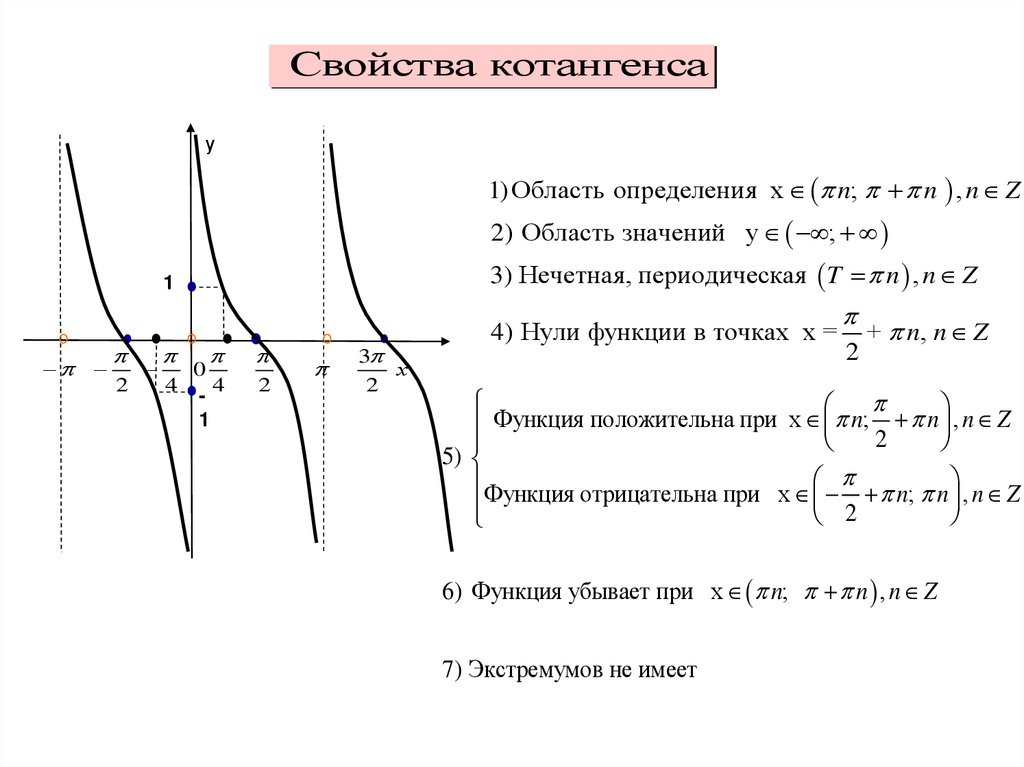
Свойства котангенса
у
1) Область определения x n; n , n Z
2) Область значений y ;
3) Нечетная, периодическая T n , n Z
1
2
0
4
4
1
2
3
х
2
4) Нули функции в точках x =
2
+ n, n Z
Функция
положительна
при
x
n
;
n
,n Z
2
5)
Функция отрицательна при x n; n , n Z
2
6) Функция убывает при x n; n , n Z
7) Экстремумов не имеет