Similar presentations:
Тригонометрические функции
1.
2. Повторение. Схема исследования функции
При исследовании функции находят:1) Область определения
Область значений
2) Четность, периодичность,
непрерывность
3) Нули функции
4) Промежутки знакопостоянства
5) Промежутки возрастания, убывания
6) Экстремумы
3.
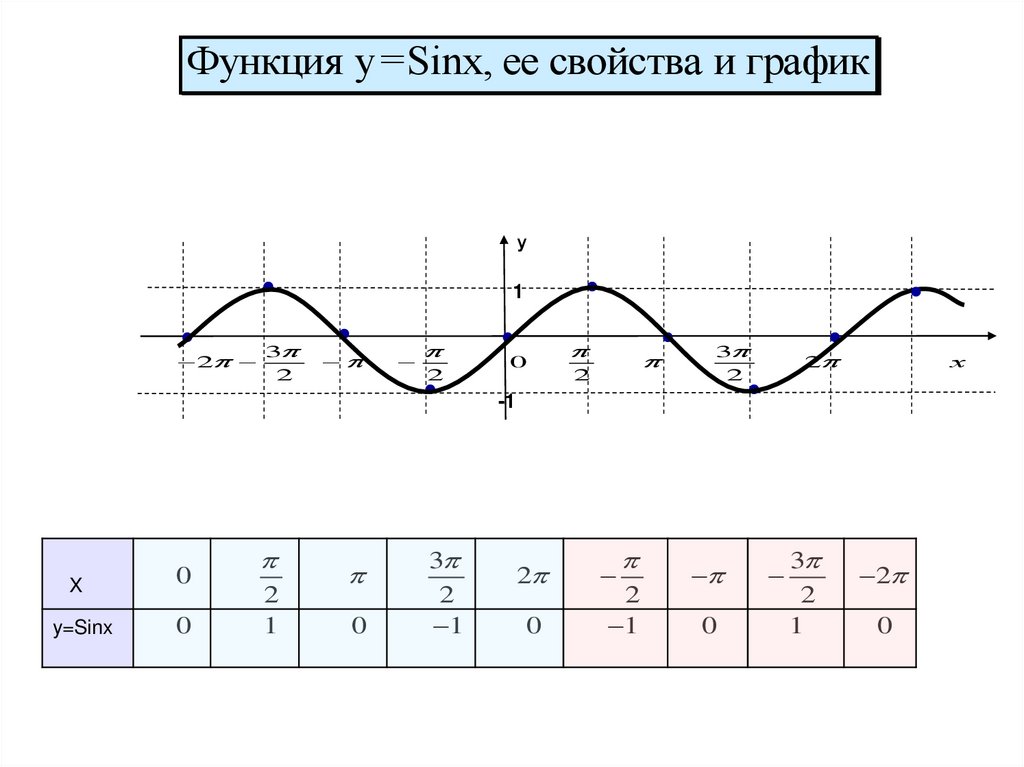
Функция y=Sinx, ее свойства и графику
1
2
3
2
2
0
2
3
2
2
х
-1
Xx
0
y
y=Sinx
0
2
1
0
3
2
1
2
0
2
1
0
3
2
1
2
0
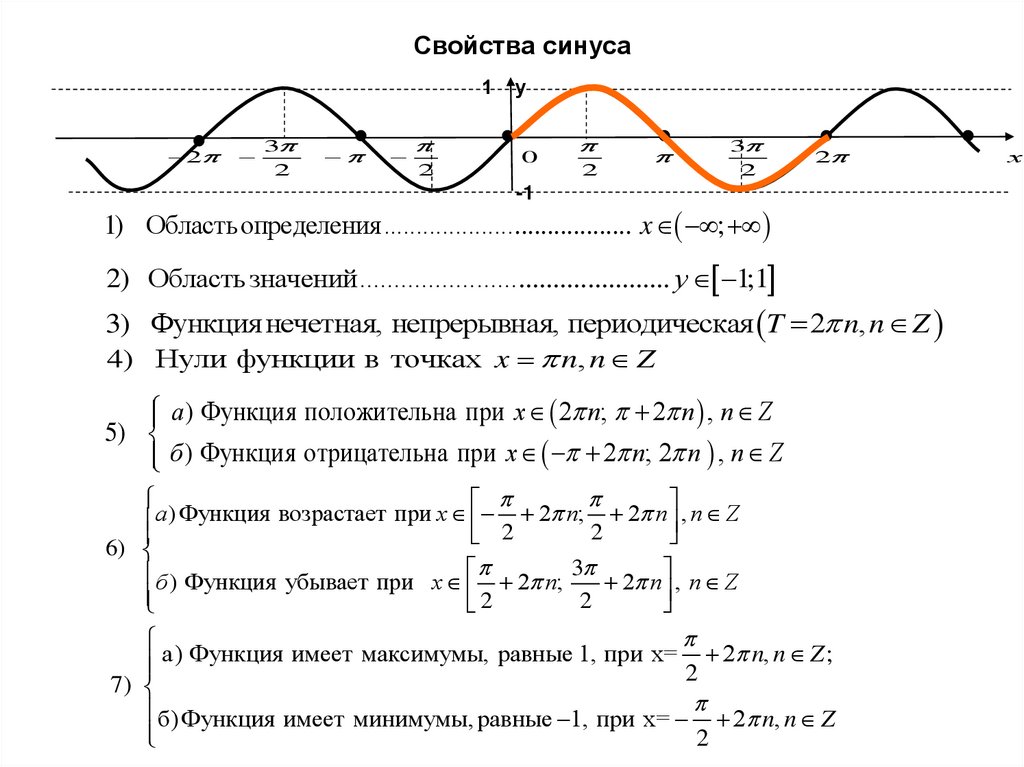
4. Свойства синуса
12
3
2
2
у
0
2
3
2
2
-1
1) Областьопределения...................................... x ;
2) Область значений............................................. у 1;1
3) Функция нечетная, непрерывная, периодическая T 2 n, n Z
4) Нули функции в точках x n, n Z
а) Функция положительна при x 2 n; 2 n , n Z
5)
б ) Функция отрицательна при x 2 n; 2 n , n Z
а
)
Функция
возрастает
при
x
2
n
;
2
n
,n Z
2
2
6)
б ) Функция убывает при x 2 n; 3 2 n , n Z
2
2
а)
Функция
имеет
максимумы,
равные
1,
при
x=
2 n, n Z ;
2
7)
б) Функция имеет минимумы, равные 1, при x= 2 n, n Z
2
х
5.
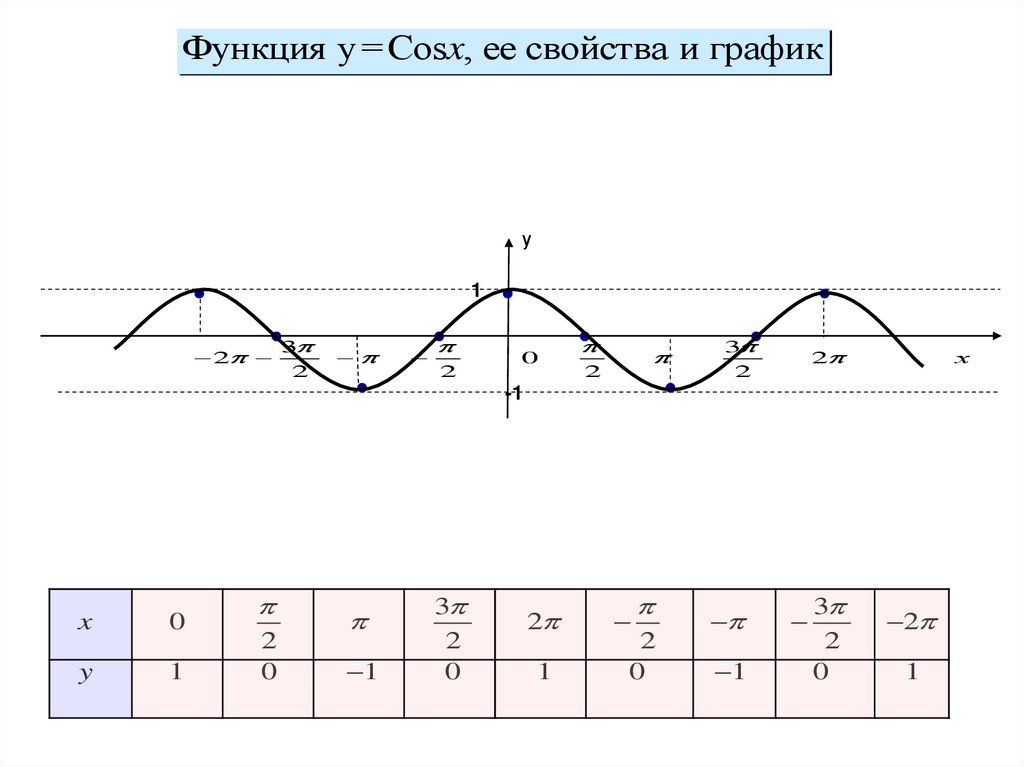
Функция y=Cosx, ее свойства и графику
1
2
3
2
2
0
2
3
2
2
х
-1
x
0
y
1
2
0
1
3
2
0
2
1
2
0
1
3
2
0
2
1
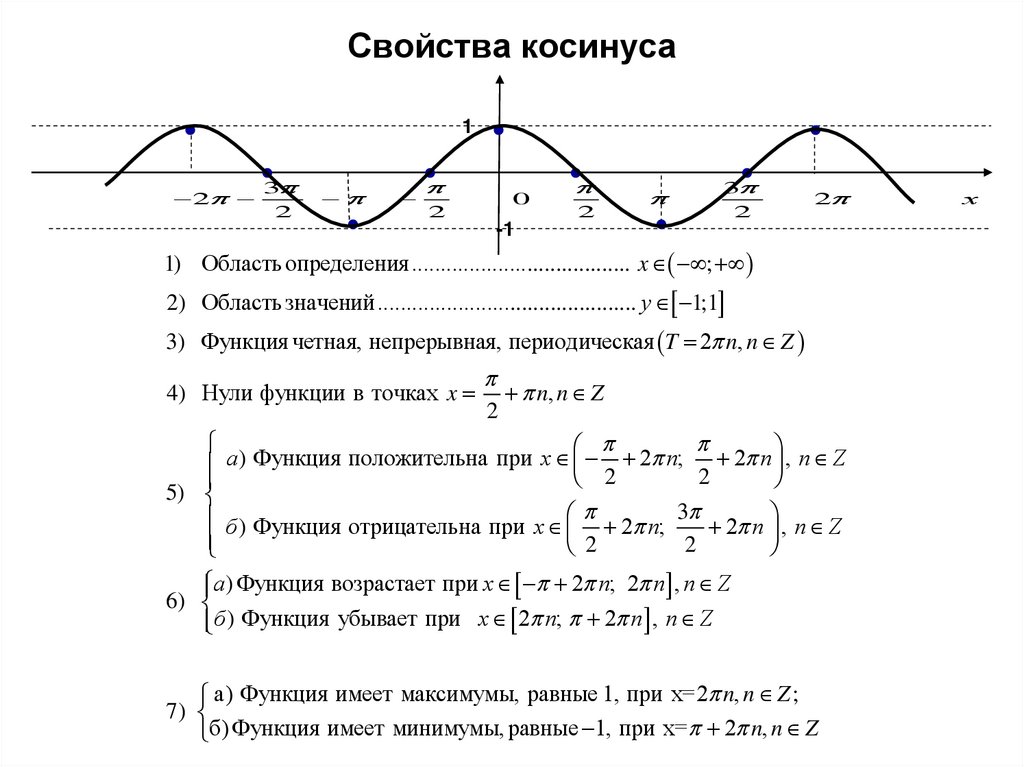
6. Свойства косинуса
12
3
2
0
2
2
3
2
2
-1
1) Область определения...................................... x ;
2) Область значений............................................. у 1;1
3) Функция четная, непрерывная, периодическая T 2 n, n Z
4) Нули функции в точках x
2
n, n Z
а
)
Функция
положительна
при
x
2
n
;
2
n
, n Z
2
2
5)
б ) Функция отрицательна при x 2 n; 3 2 n , n Z
2
2
а ) Функция возрастает при x 2 n; 2 n , n Z
6)
б ) Функция убывает при x 2 n; 2 n , n Z
а) Функция имеет максимумы, равные 1, при x=2 n, n Z ;
7)
б) Функция имеет минимумы, равные 1, при x= 2 n, n Z
х
7.
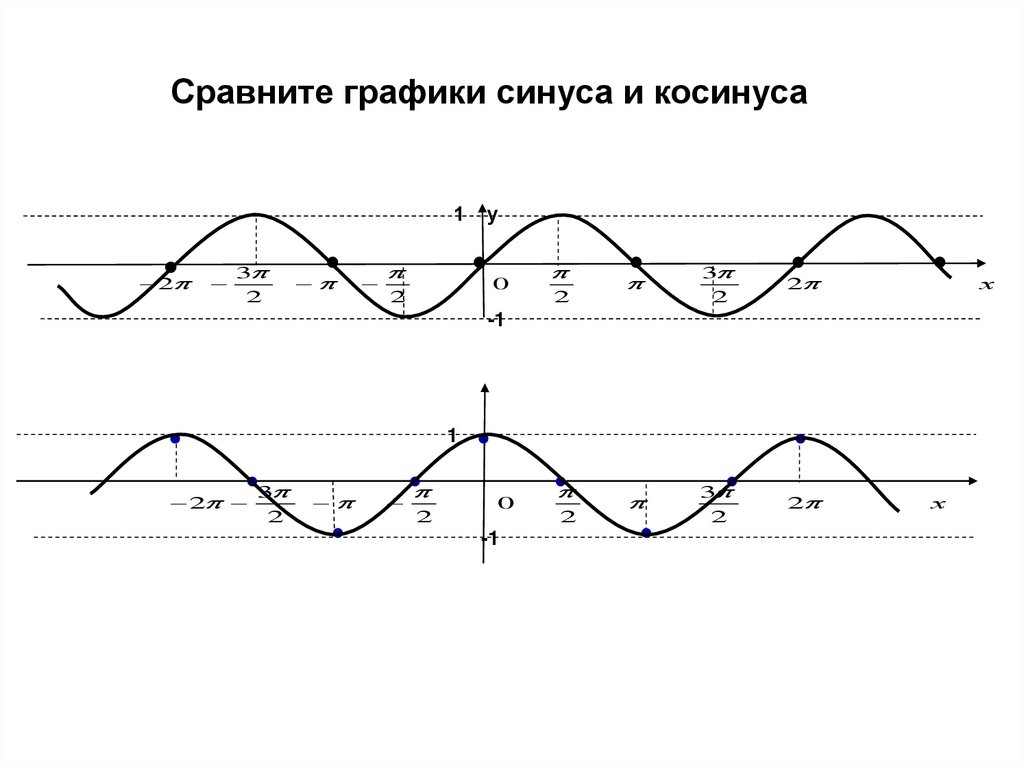
Сравните графики синуса и косинуса1
2
3
2
у
0
2
2
3
2
2
3
2
2
х
-1
1
2
3
2
2
0
-1
2
х
8.
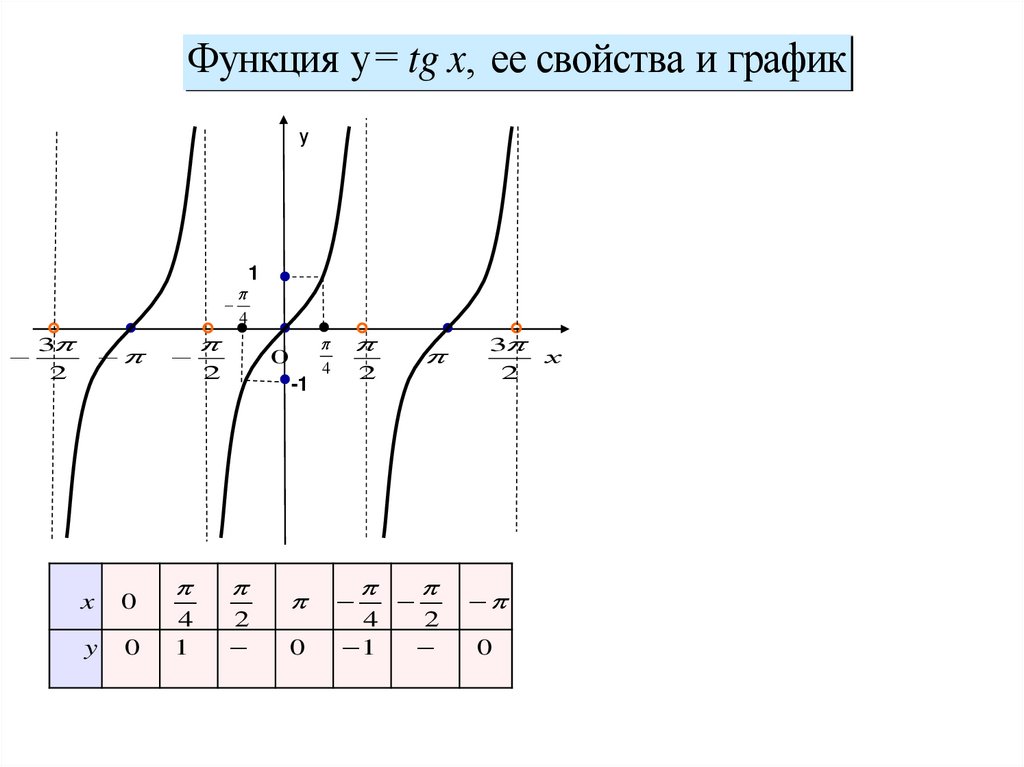
Функция y= tg x, ее свойства и графику
3
2
x
0
y
0
1
4
0
2
-1
4
1
2
0
4
2
4
1
2
3
2
0
х
9. Свойства тангенса
1) Область определения x - n; n2
2
2) Область значений y ;
у
,n Z
3) Нечетная, периодическая T n , n Z
1
3
2
2
4) Нули функции в точках x = n, n Z
4
0
-1
4
2
Функция
положительна
при
x
n
;
n
, n Z
2
5)
Функция отрицательна при x n; n , n Z
2
6) Функция возрастает при x n;
n , n Z
2
2
7) Экстремумов не имеет
3
х
2
10.
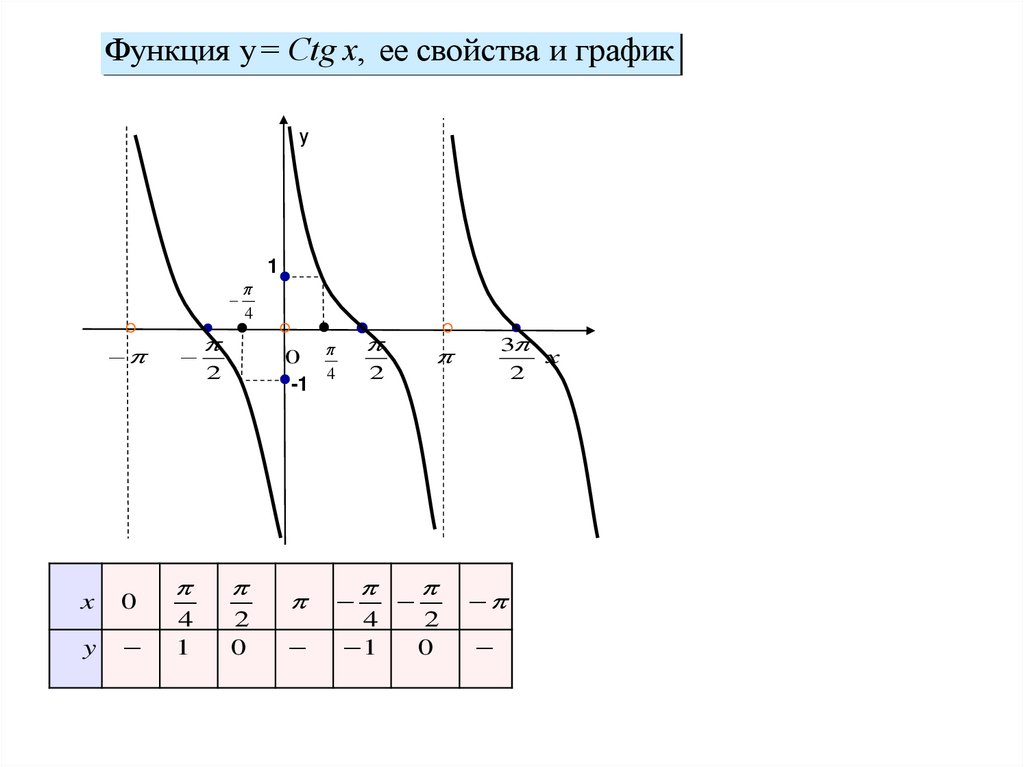
Функция y= Сtg x, ее свойства и графику
x
0
y
1
4
0
4
-1
2
4
1
2
0
2
4
1
3
х
2
2
0
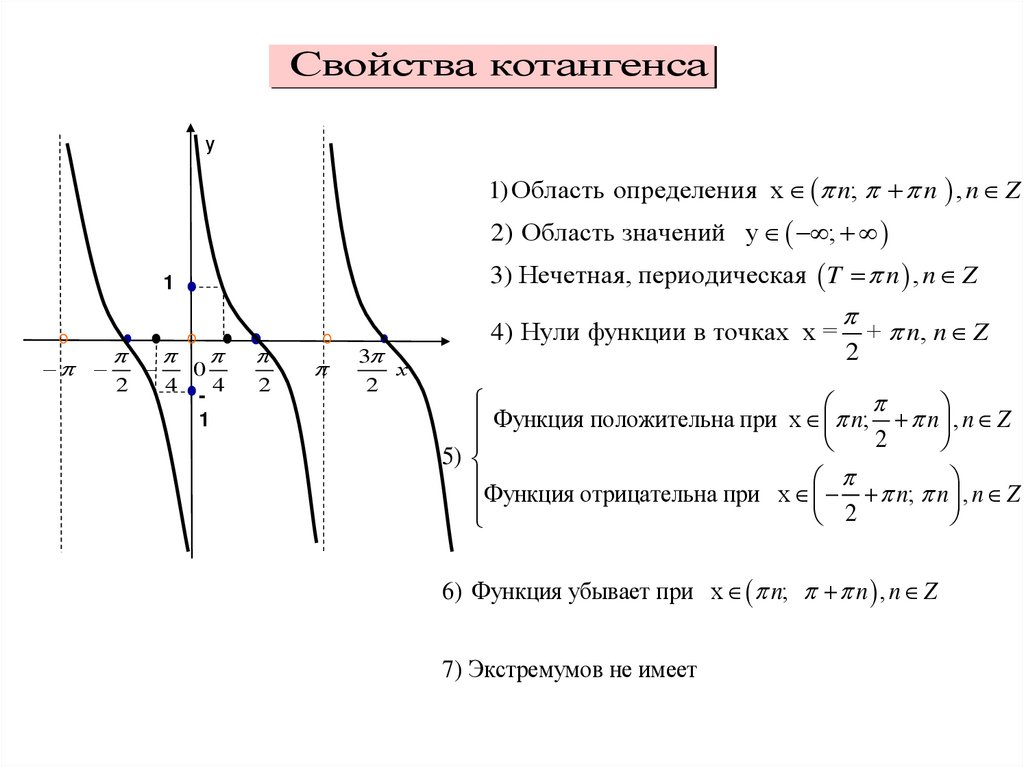
11.
Свойства котангенсау
1) Область определения x n; n , n Z
2) Область значений y ;
3) Нечетная, периодическая T n , n Z
1
2
0
4
4
1
2
3
х
2
4) Нули функции в точках x =
2
+ n, n Z
Функция
положительна
при
x
n
;
n
,n Z
2
5)
Функция отрицательна при x n; n , n Z
2
6) Функция убывает при x n; n , n Z
7) Экстремумов не имеет
12.
Преобразованияграфиков
тригонометрических
функций
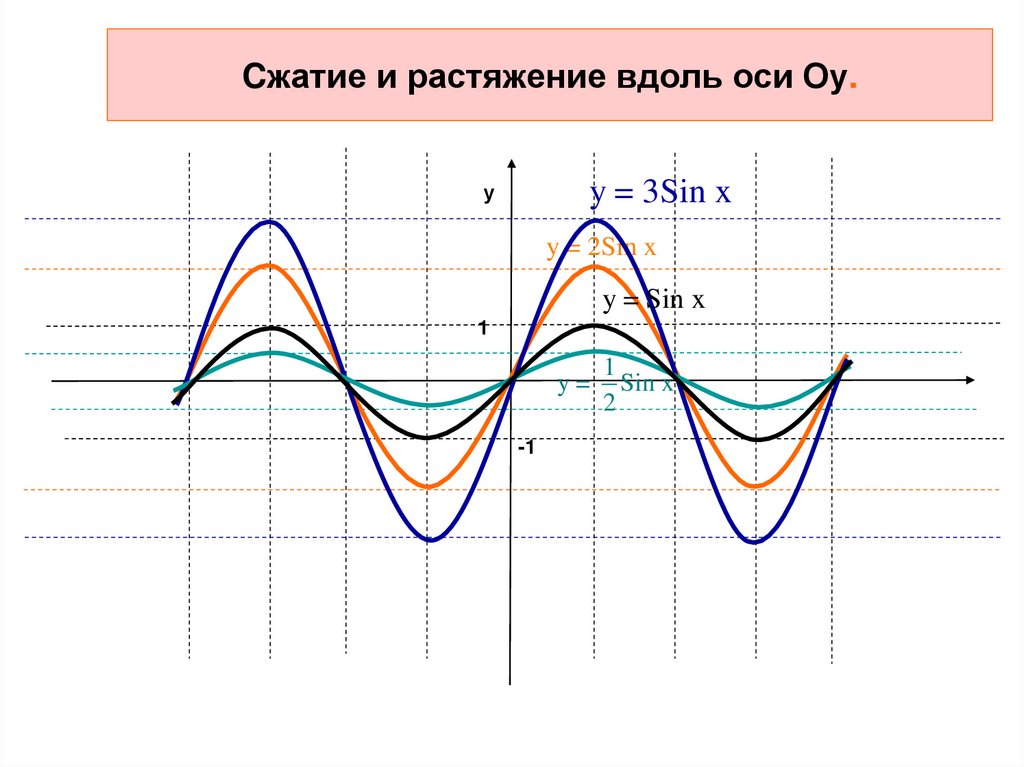
13. Cжатие и растяжение вдоль оси Оу.
y = 3Sin xу
y = 2Sin x
y = Sin x
1
y=
-1
1
Sin x
2
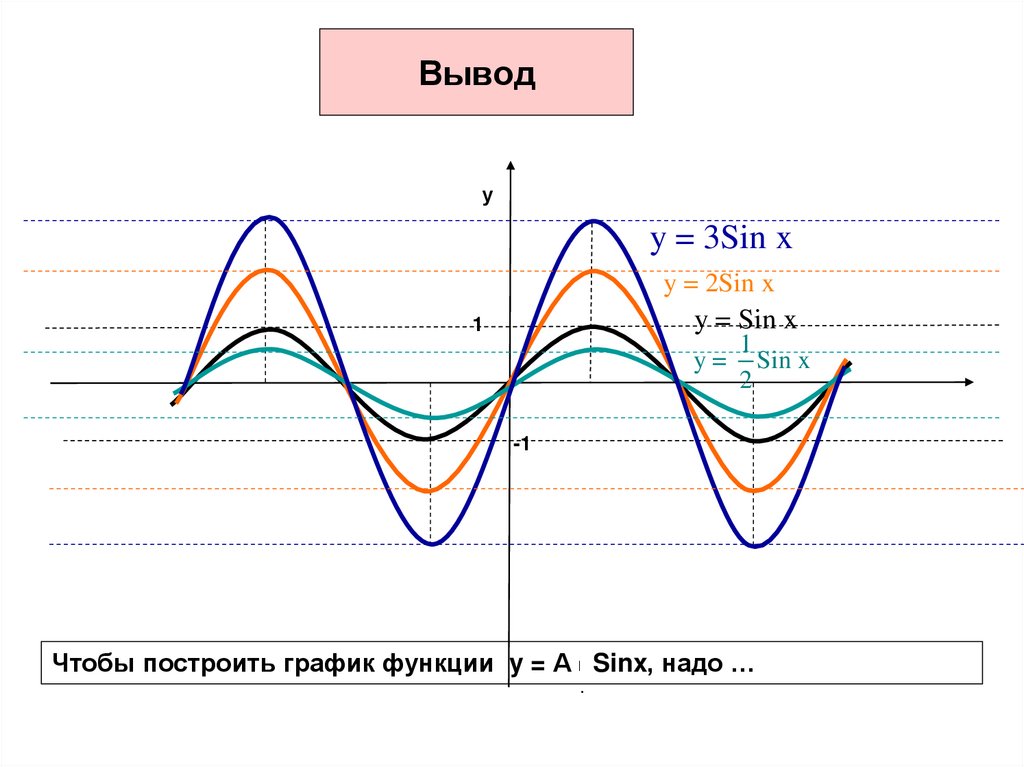
14. Вывод
уy = 3Sin x
y = 2Sin x
y = Sin x
1
y=
1
Sin x
2
-1
Чтобы построить график функции y = А Sinx, надо …
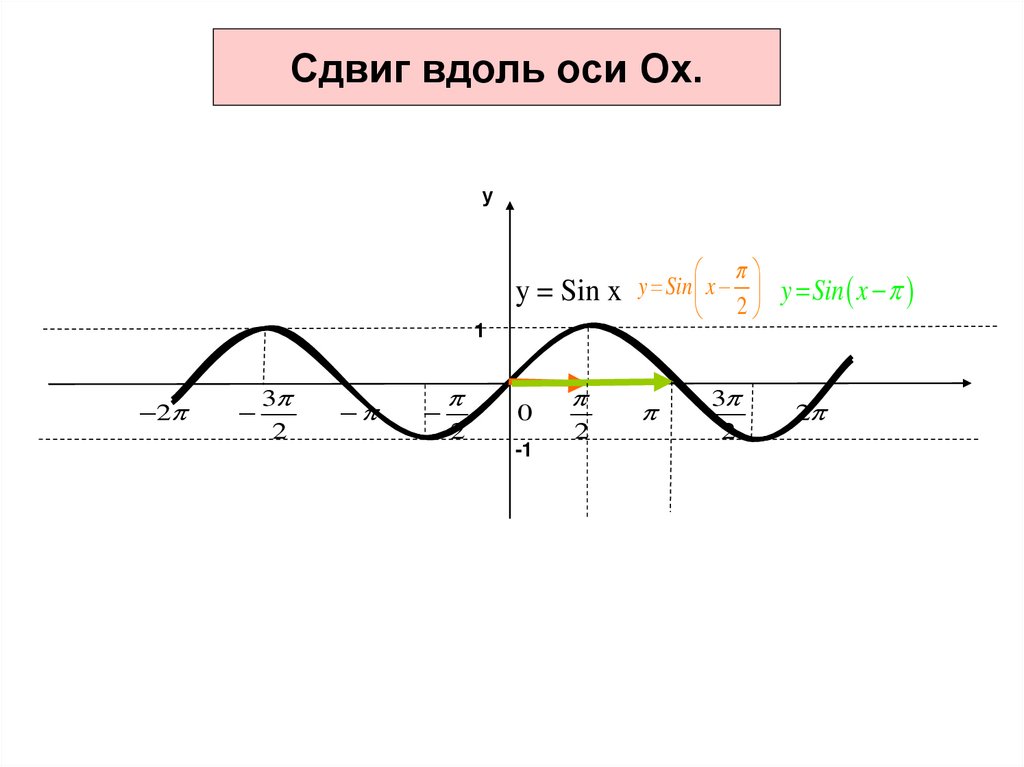
15. Сдвиг вдоль оси Ох.
уy = Sin x y Sin x 2 y Sin x
1
2
3
2
2
0
-1
2
3
2
2
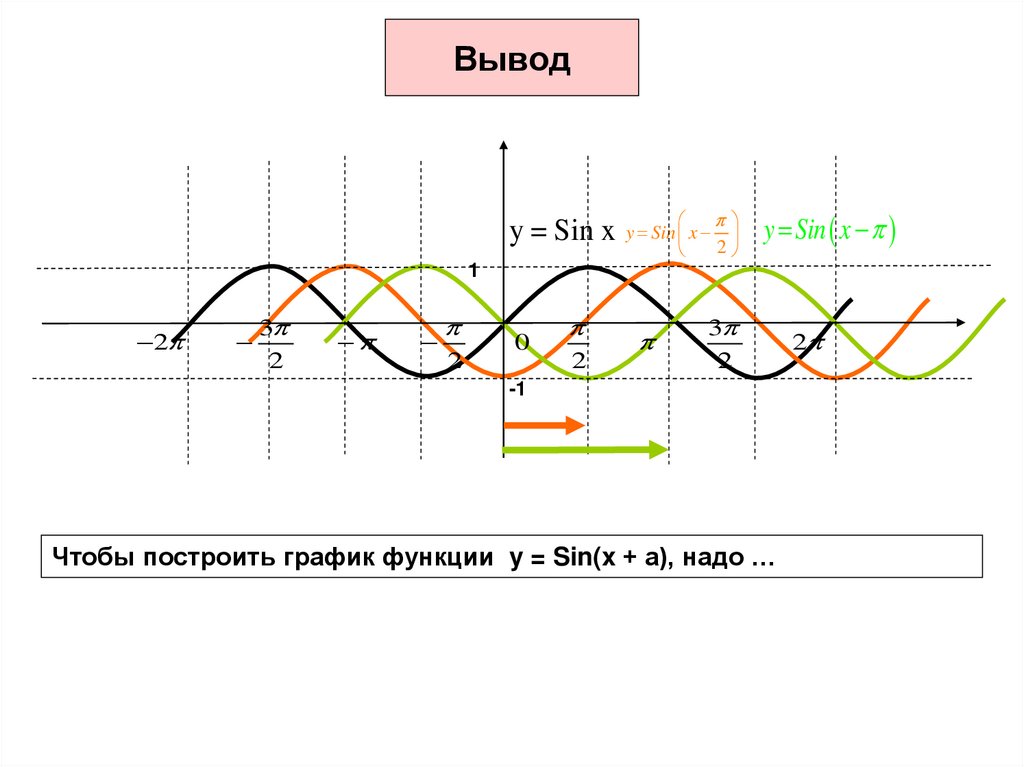
16. Вывод
y = Sin xy Sin x
2
y Sin x
1
2
3
2
2
0
2
3
2
-1
Чтобы построить график функции y = Sin(x + а), надо …
2
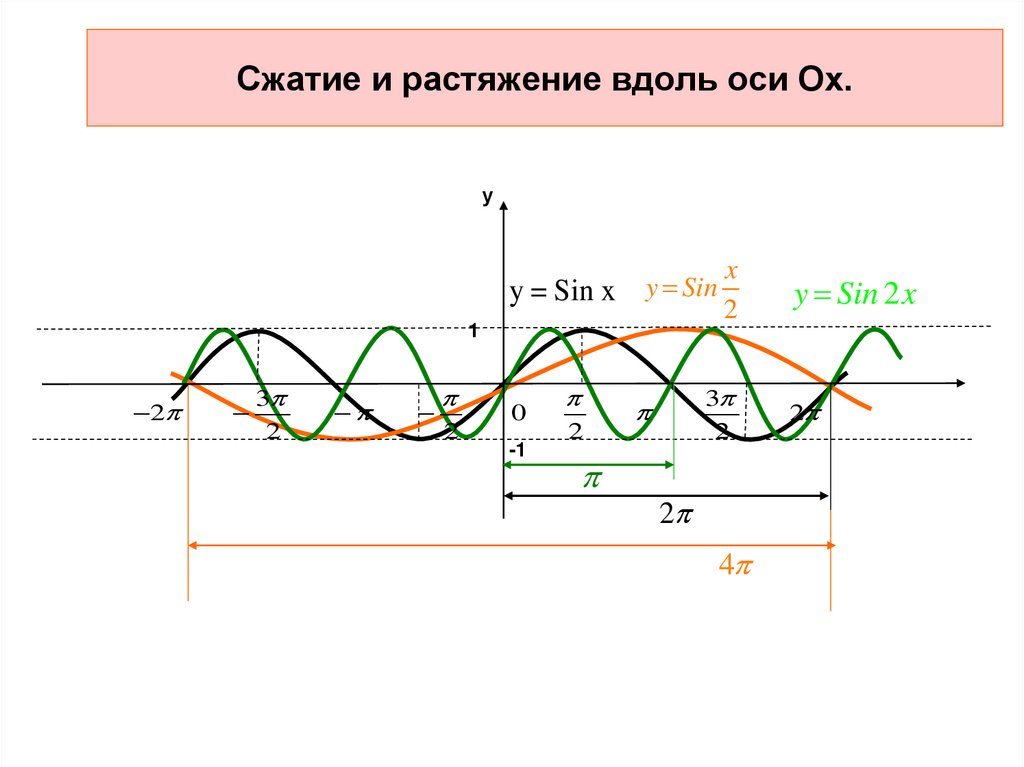
17. Сжатие и растяжение вдоль оси Ох.
уy = Sin x y Sin
1
2
3
2
2
0
-1
2
x
2
3
2
2
4
y Sin 2 x
2
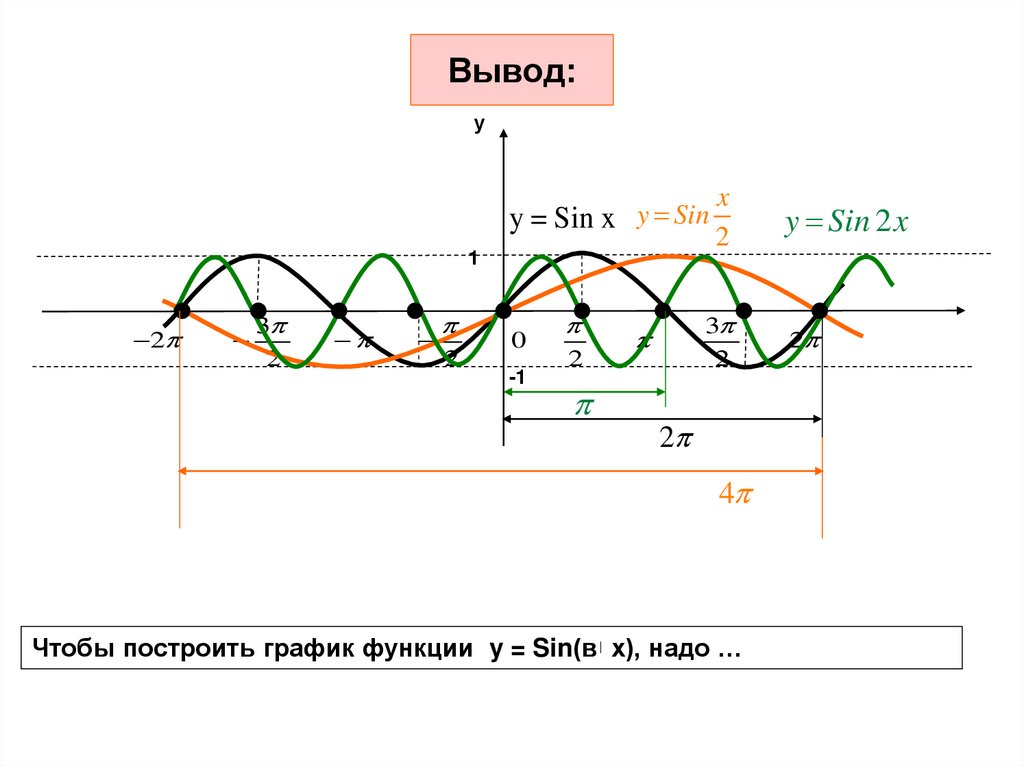
18. Вывод:
уy = Sin x y Sin
1
2
3
2
2
0
-1
2
x
2
3
2
2
4
Чтобы построить график функции y = Sin(в х), надо …
y Sin 2 x
2
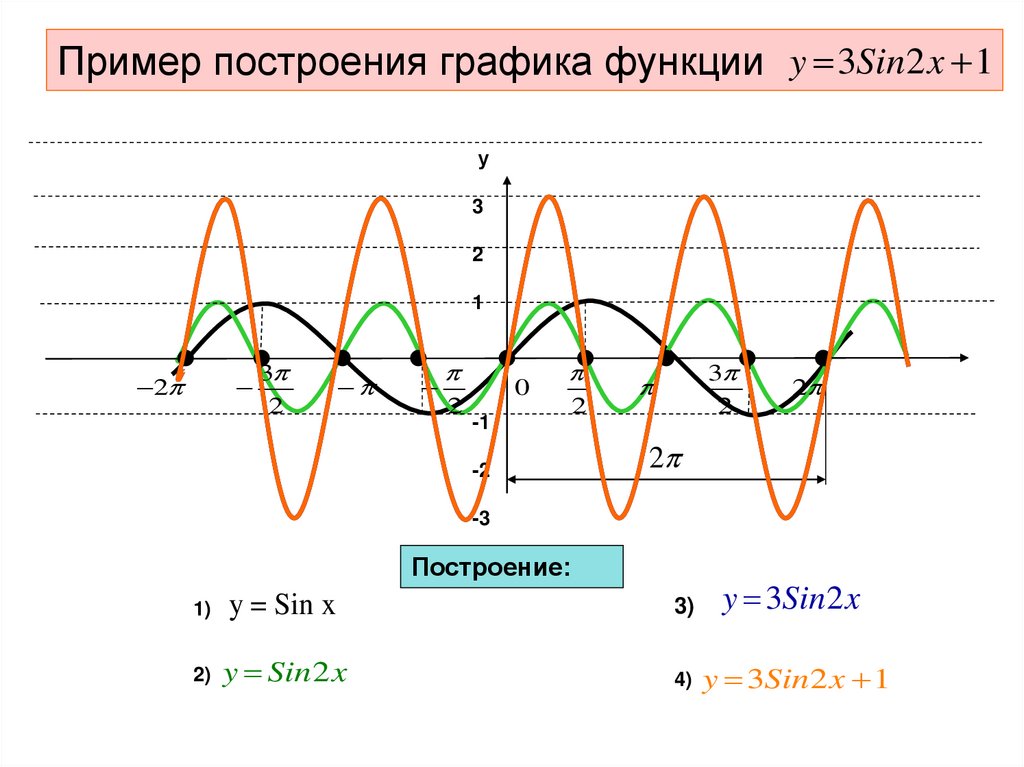
19. Пример построения графика функции
y 3Sin2 x 1у
3
2
1
2
3
2
2
0
-1
-2
2
3
2
2
2
-3
Построение:
1)
y = Sin x
3)
y 3Sin 2 x
2)
y Sin 2 x
4)
y 3Sin 2 x 1
20.
Гармонические колебания21.
Величины, изменяющиеся по законуf (t ) ASin( t )
играют важную роль.
Эту формулу называют уравнением гармонического
колебания.
А – амплитуда колебания;
- угловая частота колебания;
- начальная фаза колебания;
t – время
22.
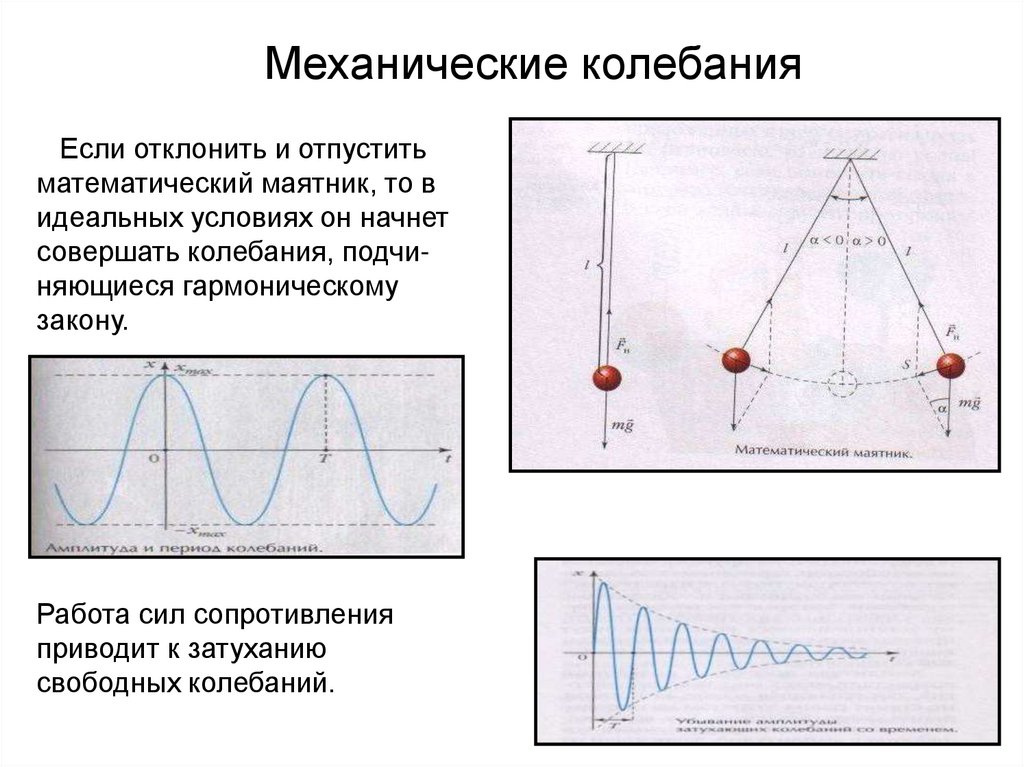
Механические колебанияЕсли отклонить и отпустить
математический маятник, то в
идеальных условиях он начнет
совершать колебания, подчиняющиеся гармоническому
закону.
Работа сил сопротивления
приводит к затуханию
свободных колебаний.
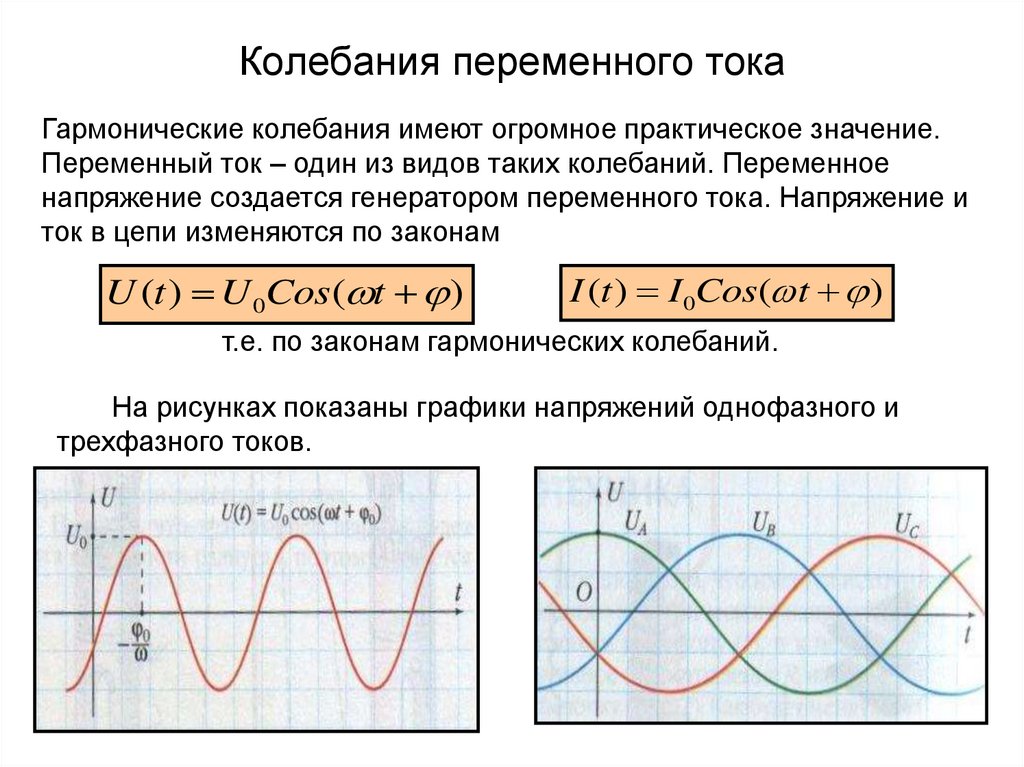
23. Колебания переменного тока
Гармонические колебания имеют огромное практическое значение.Переменный ток – один из видов таких колебаний. Переменное
напряжение создается генератором переменного тока. Напряжение и
ток в цепи изменяются по законам
U (t ) U 0Cos( t )
I (t ) I 0Cos( t )
т.е. по законам гармонических колебаний.
На рисунках показаны графики напряжений однофазного и
трехфазного токов.
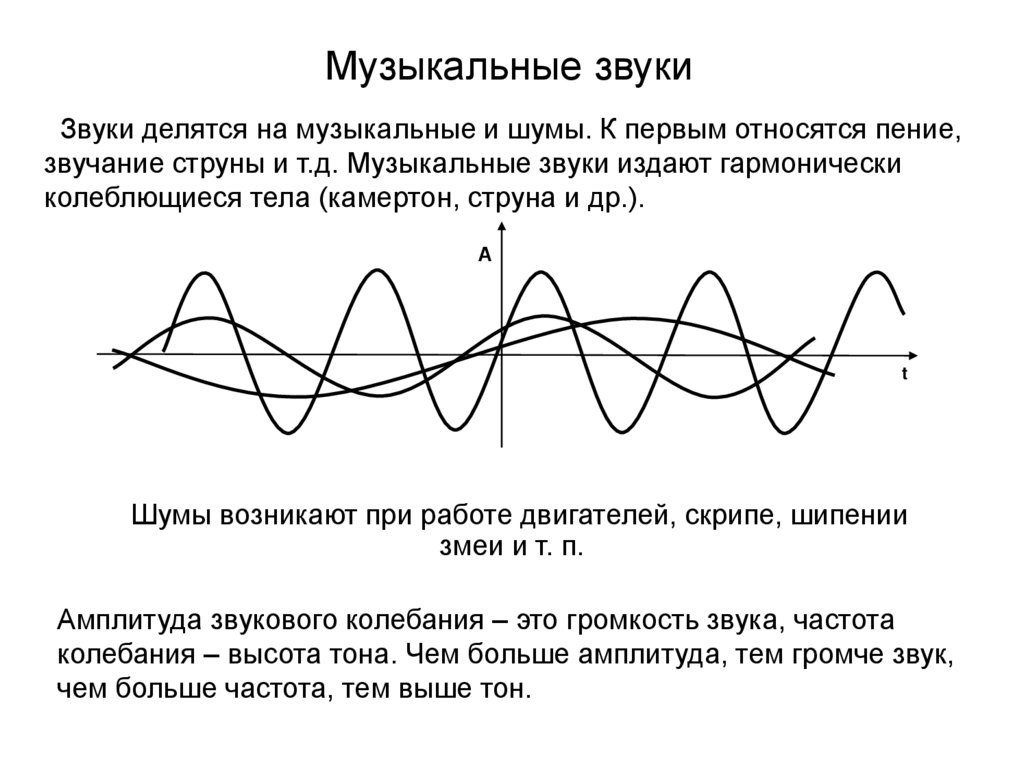
24. Музыкальные звуки
Звуки делятся на музыкальные и шумы. К первым относятся пение,звучание струны и т.д. Музыкальные звуки издают гармонически
колеблющиеся тела (камертон, струна и др.).
А
t
Шумы возникают при работе двигателей, скрипе, шипении
змеи и т. п.
Амплитуда звукового колебания – это громкость звука, частота
колебания – высота тона. Чем больше амплитуда, тем громче звук,
чем больше частота, тем выше тон.
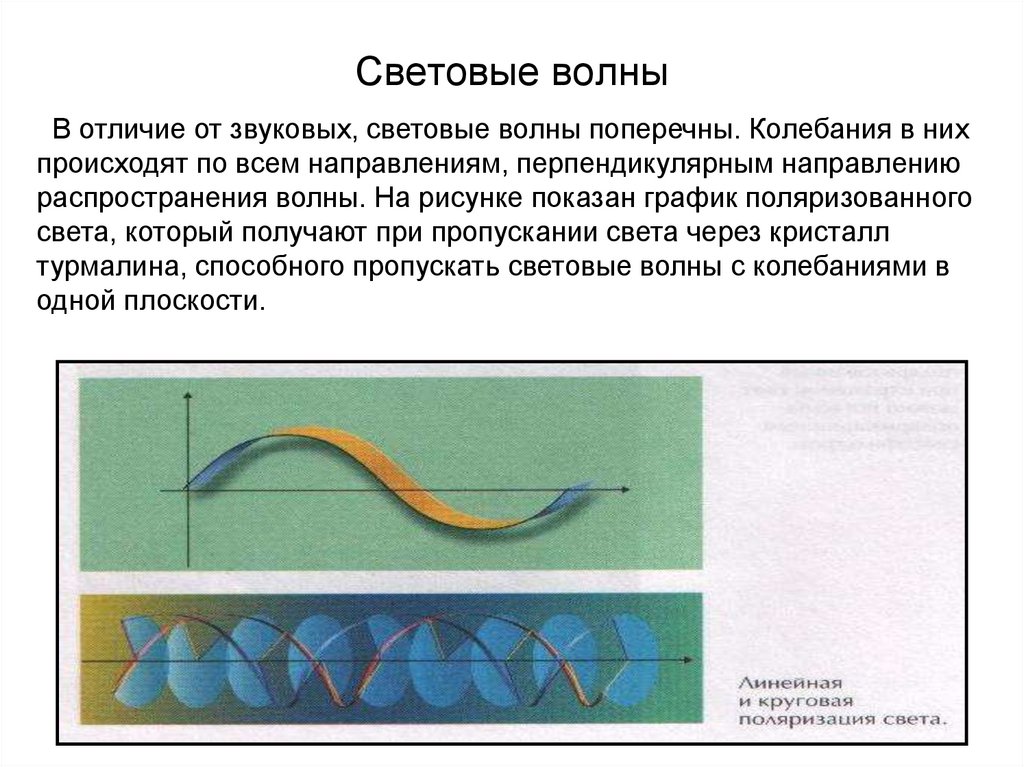
25. Световые волны
В отличие от звуковых, световые волны поперечны. Колебания в нихпроисходят по всем направлениям, перпендикулярным направлению
распространения волны. На рисунке показан график поляризованного
света, который получают при пропускании света через кристалл
турмалина, способного пропускать световые волны с колебаниями в
одной плоскости.
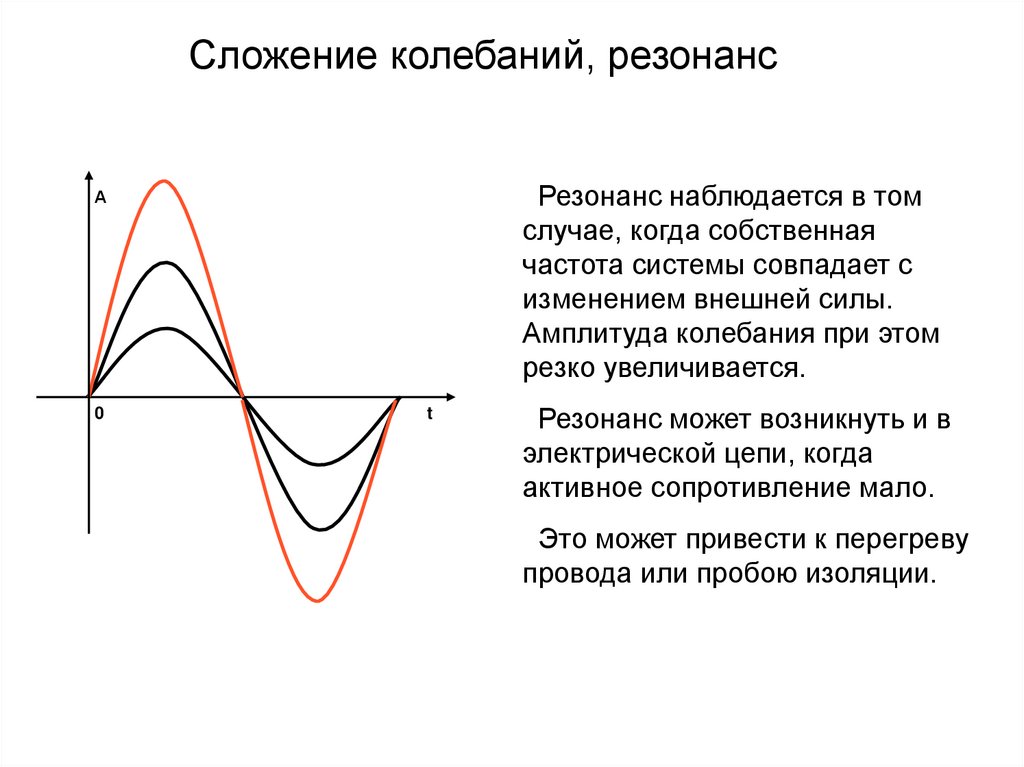
26.
Сложение колебаний, резонансРезонанс наблюдается в том
случае, когда собственная
частота системы совпадает с
изменением внешней силы.
Амплитуда колебания при этом
резко увеличивается.
А
0
t
Резонанс может возникнуть и в
электрической цепи, когда
активное сопротивление мало.
Это может привести к перегреву
провода или пробою изоляции.
27.
28.
Колебания окружают нас совсех сторон, от них не
спрятаться и не убежать.
Дрожат стены зданий,
колеблется воздух, полный
звуков, волнуются моря и
озера. Колебания – это
универсальные процессы
природы!
29. Задание на дом
1) Яковлев Г.Н. «Алгебра и началаанализа» §26
x
2) Постройте график функции y 2Cos 1
2
3) Сформулируйте свойства этой функции
30. Пробная работа
Постройте график функции y = -2Sin xи сформулируйте ее свойства
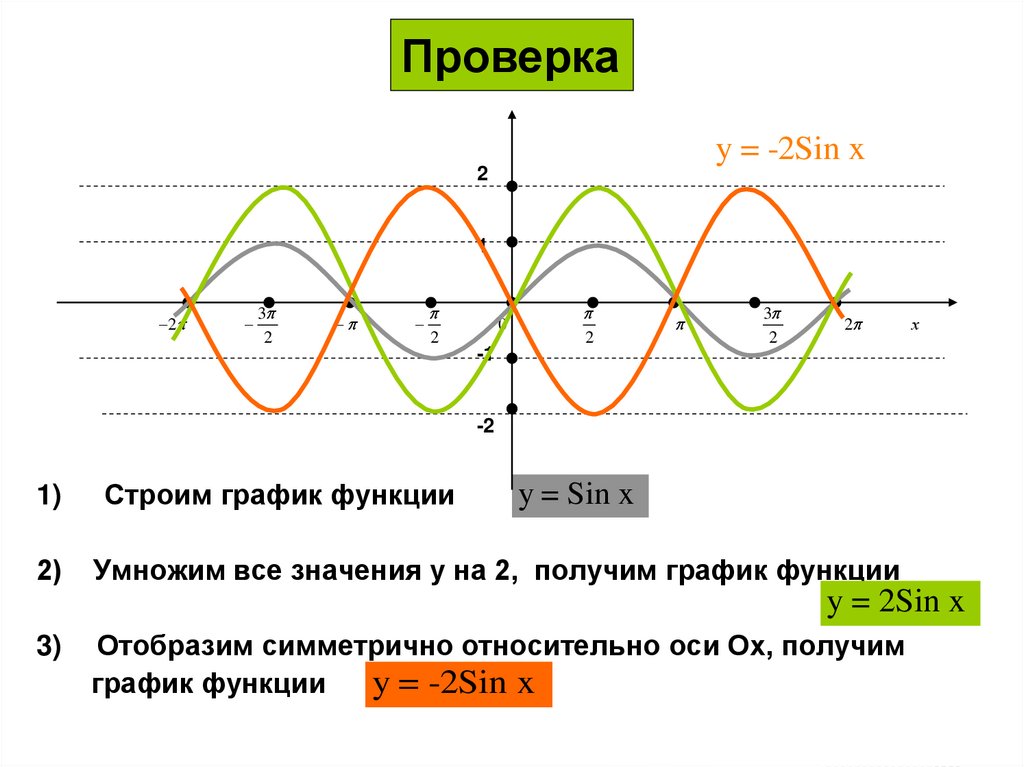
31. Проверка
y = -2Sin x2
1
2
3
2
2
0
-1
2
3
2
2
х
-2
1)
2)
Строим график функции
y = Sin x
Умножим все значения у на 2, получим график функции
y = 2Sin x
3)
Отобразим симметрично относительно оси Ох, получим
график функции
y = -2Sin x
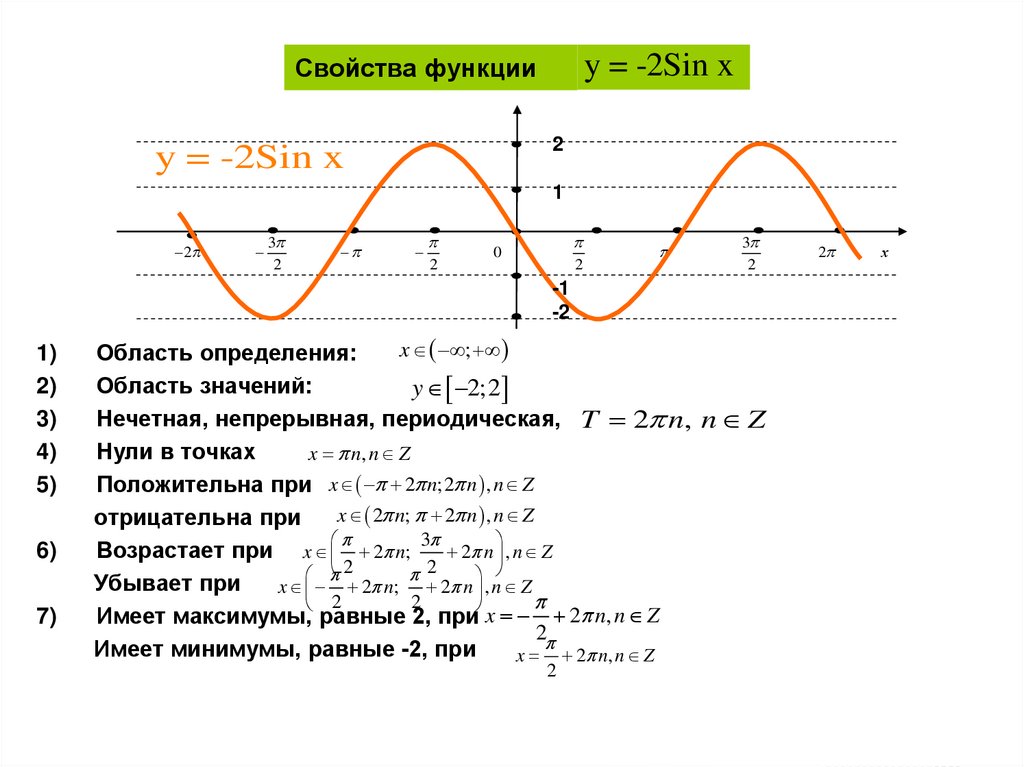
32. Свойства функции
y = -2Sin xСвойства функции
2
y = -2Sin x
1
2
3
2
2
0
2
3
2
-1
-2
1)
2)
3)
4)
5)
6)
7)
x ;
Область определения:
Область значений:
y 2; 2
Нечетная, непрерывная, периодическая, T 2 n, n Z
Нули в точках
x n, n Z
Положительна при x 2 n;2 n , n Z
x 2 n; 2 n , n Z
отрицательна при
3
2 n , n Z
Возрастает при x 2 n;
2
2
Убывает при
x 2 n; 2 n , n Z
2
2
Имеет максимумы, равные 2, при x 2 n, n Z
2
Имеет минимумы, равные -2, при
x 2 n, n Z
2
2
х











 mathematics
mathematics








