Тепловое излучение. Лекция 30

1.

КВАНТОВАЯ ОПТИКА
Лекция 30.
Тема: Тепловое излучение
Учебник:
Трофимова Т.И. Курс физики : учеб. пособ. для вузов / Т. И.
Трофимова. - М.: Академия, 2007.- с. 357-368.
Курочкин А.Р.
к.ф.-м.н.

2.

Существуют два вида излучения.
Тепловое излучение – испускание
электромагнитных волн за счёт
внутренней (тепловой)
энергии тел.
Люминесценция – излучения,
возбуждаемые за счёт любого вида энергии,
кроме тепловой.
2

3.

Виды люминесценции
- хемилюминесценция (свечение окисляющегося
на воздухе фосфора за счёт энергии, выделяемой
при химическом превращении);
- электролюминесценция (свечение, возникающее
в газах и твёрдых телах под воздействием
электрического поля);
- фотолюминесценция (свечение, возбуждаемое
поглощаемым
телом
электромагнитным
излучением).
3

4.

Тепловое излучение
имеет место при любой температуре!
излучающее
тело
оболочка с
идеально
отражающей
поверхностью
внутри вакуум
Тепловое излучение - единственный вид излучения,
которое может находится в равновесии
с излучающим телом.
4

5.

Равновесность означает,
что тело в единицу времени
поглощает столько же энергии,
сколько и излучает.
Почему тепловое излучение равновесно?
Потому что любое нарушение равновесия
в системе тело-излучение
вызывает возникновение процессов,
восстанавливающих равновесие.
5

6.

Энергетическая светимость RT – энергия, излучаемая
единицей поверхности излучающего тела за единицу времени
по всем направлениям.
(Мощность излучения с единицы площади поверхности тела)
W
P
RT
S t S
Вт
Дж
2
м с м 2
W – энергия, излучаемая всей поверхностью тела [Дж];
S – площадь поверхности [м2];
P – мощность излучения [Вт];
t – время излучения [с].
Энергетическая светимость RT – функция температуры T.
6

7.

Лучеиспускательная способность rν,T – часть его
энергетической
светимости,
приходящейся
на
единичный интервал частот или длин волн.
r , T
R ,T
Дж
м 2
или
r , T
R ,T
Дж
м3 с
Лучеиспускательная способность rν,T
частоты ν и температуры T.
– функция
7

8.

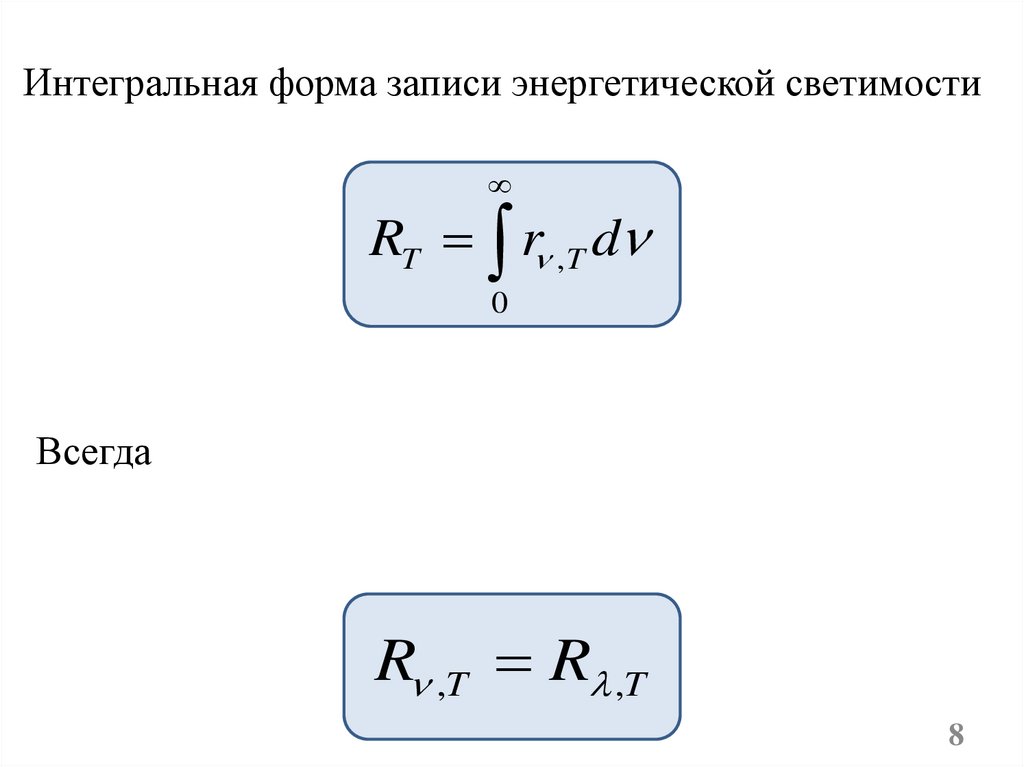
Интегральная форма записи энергетической светимости
RT r ,T d
0
Всегда
R ,T R ,T
8

9.

Как перейти от rν,T к rλ,T ?
Учтём, что
с
, тогда
d
d c
c
2 .
d
d
c
2
Знак «-» учитывает,
что с ростом одной величины (λ или ν),
другая величина убывает.
9

10.

Перепишем выражения в виде
dR ,T r ,T d
dR ,T r ,T d
r ,T d r ,T d
r ,T r ,T
.
Воспользовавшись соотношением, получим
r ,T
2
с
r ,T
10

11.

Спектральной поглощательная способность тела Aν,T
Пусть на элементарную площадку поверхности тела падает
лучистая энергия, переносимая электромагнитными волнами,
частота которых заключена в интервале ν, ν+dν.
Часть данной энергии будет поглощена телом.
dW , d
dW погл
, d
- лучистая энергия, падающая на поверхность тела.
- лучистая энергия, поглощённая поверхностью тела.
A ,T
dW погл
, d
dW , d
Спектральная поглощательная способность Aν,T –
функция частоты ν и температуры T.
11

12.

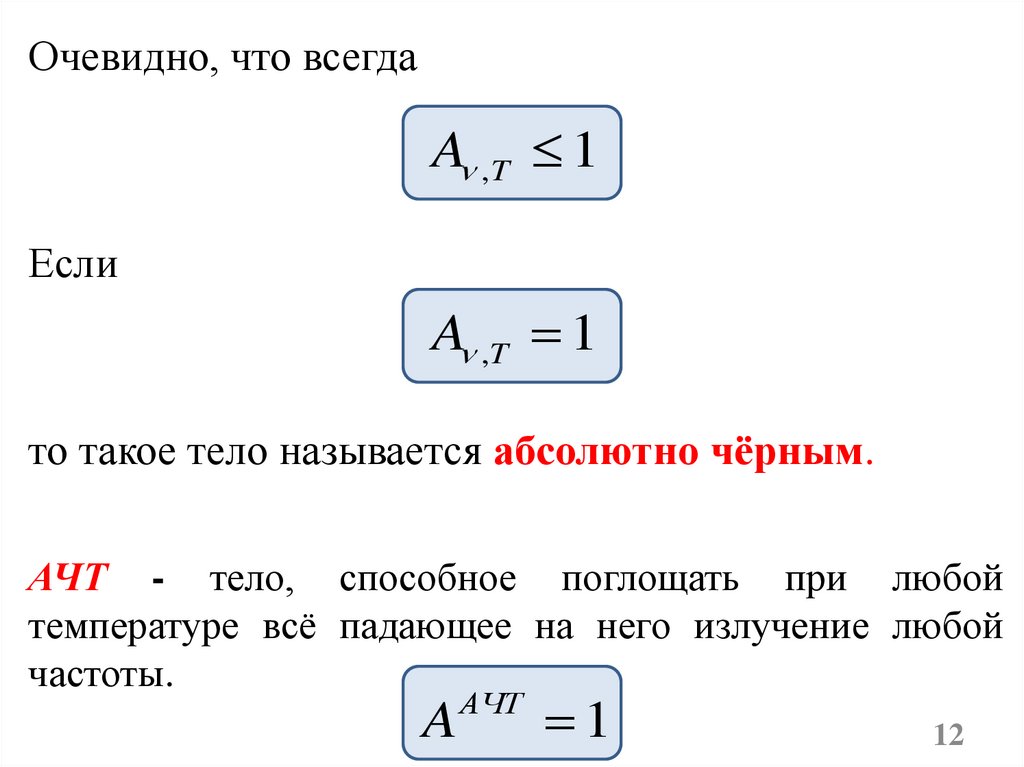
Очевидно, что всегда
A ,T 1
Если
A ,T 1
то такое тело называется абсолютно чёрным.
АЧТ - тело, способное поглощать при любой
температуре всё падающее на него излучение любой
частоты.
A
АЧТ
1
12

13.

Наиболее близкими телами к АЧТ можно назвать:
• чёрный бархат;
• сажа (уголь) поглощает 96% света;
• Vantablack - субстанция из углеродных нанотрубок.
Поглощает 99,965% падающего на него излучения.
Пример: при наличии небольшого
отверстия в замкнутой полости, свет,
попавший туда, будет испытывать
многократные
отражения
и
практически полностью поглотится.
13

14.

Серое тело - тело, поглощательная способность
которого меньше единицы, но одинакова для всех частот
и зависит только от температуры, материала и состояния
поверхности тела:
A 1
c
T
14

15.

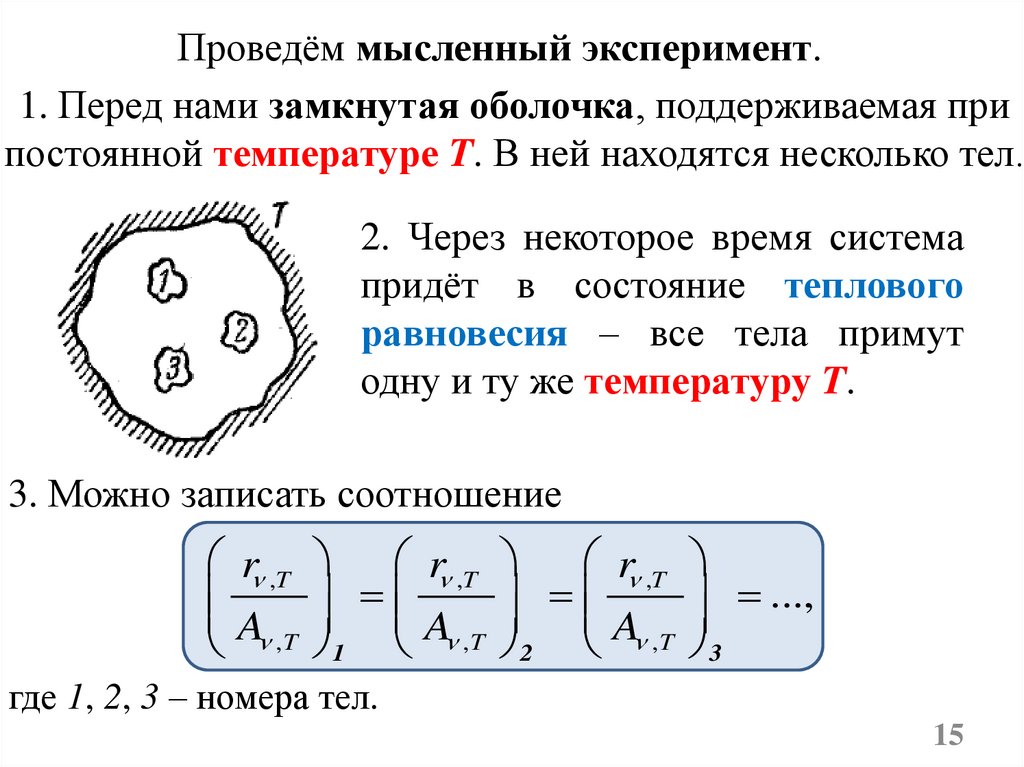
Проведём мысленный эксперимент.
1. Перед нами замкнутая оболочка, поддерживаемая при
постоянной температуре T. В ней находятся несколько тел.
2. Через некоторое время система
придёт в состояние теплового
равновесия – все тела примут
одну и ту же температуру T.
3. Можно записать соотношение
r ,T
A ,T
r ,T
1 A ,T
r ,T
2 A ,T
...,
3
где 1, 2, 3 – номера тел.
15

16.

Закон Кирхгофа
а. Отношение лучеиспускательной
к
поглощательной способности тела не
зависит от природы тела и является
универсальной для всех тел функцией
частоты (длины волны) и температуры:
r ,T
A ,T
Кирхгоф
Густав Роберт
(1824-1887)
f , T
16

17.

Определим вид универсальной функции Кирхгофа
Применим закон Кирхгофа к АЧТ
Для АЧТ
A
АЧТ
АЧТ
,T
АЧТ
r
A
1
АЧТ
,T
r
1
f , T r , T
АЧТ
Таким образом, универсальная функция Кирхгофа есть
лучеиспускательная способность АЧТ.
б. Для всех тел, отношение лучеиспускательной способности к
спектральной
поглощательной
способности
равно
лучеиспускательной способности абсолютно черного тела при той
же температуре.
r ,T
A ,T
r , T
АЧТ
17

18.

Величины rν,T и Aν,T могут меняться
очень сильно при переходе
от одного тела к другому.
Но отношение этих величин
одинаково для всех тел!
Тело, сильнее поглощающее какие-либо лучи,
будут эти лучи сильнее и испускать.
18

19.

Энергетическая светимость серого тела
c
r
,
T
c
c
АЧТ
RT r ,T d c r ,T
A ,T
0
A
c
,T
0
r
АЧТ
,T
d A
c
T
r
АЧТ
,T
d A R
c
T
АЧТ
T
0
19

20.

Закон Стефана-Больцмана
Стефан
Йозеф
(1835-1893)
Больцман
Людвиг
(1844-1906)
Энергетическая светимость чёрного тела пропорциональна
четвёртой степени его термодинамической температуре.
АЧТ
T
R
5, 67 10
8
T
4
Вт
– постоянная Стефана-Больцмана;
2
4
м К
T – термодинамическая температура [К].
20

21.

Закон смещения Ви́на
Длина
волны,
соответствующая
максимальному
значению
лучеиспускательной
способности
АЧТ,
обратно пропорциональна его абсолютной
температуре. r
АЧТ
,T
max
b
T
max
Вин
Вильгельм
(1864 - 1928)
Спектр АЧТ – распределение
лучеиспускательной способности
АЧТ по длинам волн.
λmax – длина волны, соответствующая максимальному
значению лучеиспускательной способности АЧТ [м];
b=2,9·10-3 – постоянная Ви́на [м·К];
T – температура [К].
21

22.

Закон смещения Ви́на показывает смещение положения
АЧТ
r
максимума функции r АЧТ
,T по мере возрастания
,T
температуры в область коротких длин волн.
r АЧТ
,T
r АЧТ
,T
1max 2 max 3max
Площадь фигуры под графиком
АЧТ
есть энергетическая светимость RT .
22

23.

Наглядный пример – цвет звёзд
Цвет любой звезды зависит только от
температуры её внешних слоев – того, что мы
называем «поверхностью» звезды.
1. Холодные
светила,
с
температурой
поверхности 2-3 тысячи градусов, имеют
красный цвет.
2. Температура поверхности солнца – «жёлтого
карлика», около 6 тысяч градусов.
Длина
волны λ
уменьшается
с
увеличением
температуры
3. Температура голубых звёзд может достигать
40 тысяч градусов и выше.
23

24.

Созвездие Ориона
Звезда Бетельгейзе
красного цвета
Звезда Ригель
голубовато-белого цвета 24

25.

Какой математический вид имеет универсальная
функция Кирхгофа?
АЧТ
r , T
?
r АЧТ
,T
25

26.

Формула Рэлея-Джинса
Рэлей
и
Джинс
получили
зависимость r АЧТ
от частоты света,
,T
используя методы классической
статистической физики.
Джинс
Джеймс Хопвуд
(1877 - 1946)
Стретт, Джон Уильям
(лорд Рэлей)
(1842 - 1919)
Они предположили, опираясь на теорему о равнораспределении
энергии по степеням свободы, что на каждое электромагнитное
колебание приходится в среднем энергия равная kT.
АЧТ
,T
r
2
2 kT
c
2
k=1,38·10-23 – постоянная Больцмана [Дж/К];
T – абсолютная температура [К].
26

27.

r АЧТ
,T
Экспериментальная
кривая
Формула Рэлея-Джинса согласуется с экспериментом
только в области малых частот и больших
температур.
27

28.

Попробуем получить закон Стефана-Больцмана из
формулы Рэлея-Джинса
АЧТ
,T
r
2
2 kT
c
2
АЧТ
T
R
r
АЧТ
,T
0
RTАЧТ T 4
2 kT
2
d
d
2
c 0
Мы видим, что RTАЧТ неограниченно растёт, достигая
чрезвычайно больших значений в ультрафиолете
(7,5·1014-3·1017 Гц).
Этот результат получил название «ультрафиолетовая
катастрофа».
28

29.

Эта неудача свидетельствовала о
недостатках
в классической теории физики.
29

30.

РЕВОЛЮЦИЯ В ФИЗИКЕ. 1900 ГОД.
Квантовая гипотеза Планка
Атомные осцилляторы излучают энергию не непрерывно, а
дискретно, определёнными порциями – квантами.
E h
hc
- энергия кванта.
h=6,625·10-34 – постоянная Планка [Дж·с];
с=3·108 – скорость света в вакууме [м/с];
λ – длина волны света [м].
ν – частота волны света [Гц].
30

31.

Поскольку энергия излучается порциями, то энергия
осциллятора может принимать лишь определённые
дискретные значения, кратные целому числу квантов:
E nh
n 0,1, 2
Формула Планка
а.
f , T r , T
АЧТ
2 h
2
c
3
1
e
h
kT
1
Формула Планка, хорошо согласуется с экспериментальными
данными по распределению энергии в спектре излучения
АЧТ, во всём интервале частот и температур.
31

32.

б.
f , T r , T
АЧТ
2 c h
2
1
5
e
hc
kT
1
Особый случай h
kT . Энергия кванта очень
мала по сравнению с энергией теплового
движения kT.
e
h
kT
h
1
kT
Формула Планка переходит в формулу РэлеяДжинса.
32

33.

Доказательство.
e
h
kT
h
1
kT
*
Подставим (*) в формулу Планка
АЧТ
r , T
2 h 1
2
2 kT
2
h
c
c
kT
3
формула Рэлея-Джинса
2
33

34.

Получим из формулы Планка формулу СтефанаБольцмана.
АЧТ
T
R
r , T
АЧТ
0
2 h
d
2
c
0
3
1
e
h
kT
d
1
Введём безразмерную переменную
h
h
kT
x
; dx
d ; d
dx.
kT
kT
h
34

35.

Тогда формула будет записана
R
где
АЧТ
2 k 4 x
4
2 3 T x dx T ,
ch
e 1
0
4
4
2 k
2 3
c h
3
x
2 k
0 e x 1dx 15c 2 h3 ,
3
5
4
так как
x
0 e x 1dx 15 .
3
4
формула
Стефана-Больцмана
35

36.

Получим из формулы Планка закон Ви́на с
помощью (7) и (17)
r , T
АЧТ
c
2
АЧТ
r , T
2 c
2
1
5
откуда
e
h
kT
hc
АЧТ
e
2
r , T
2 c h
kT
5
hc
hc
kT
2 kT
e
1
e 1
,
1
hc
kT
20 .
36

37.

Приравняем к нулю производную (20) и найдём λmax.
hc
xe 5 e 1 0 ввели x
.
kT max
x
x
Решением этого трансцендентного уравнения будет
Откуда
Трансцендентное уравнение –
уравнение, не являющееся
алгебраическим. Это уравнения,
содержащие показательные,
логарифмические,
тригонометрические функции.
x 4,965.
T max
hc
b.
4,965k
закон смещения Ви́на
37

38.

Заключение
Формула Планка
• хорошо согласуется
данными, но и
с
экспериментальными
• содержит в себе частные законы теплового
излучения, а также
• позволяет вычислить постоянные в законах
теплового излучения.
38