Similar presentations:
Определение логарифма
1.
2.
«Изобретение логарифмов,сокращая вычисления
нескольких месяцев в труд
нескольких дней словно
удваивает жизнь астрономов»
П.С. Лаплас
3.
Цель урокаПознакомиться с понятием
логарифма,
основным логарифмическим
тождеством;
научиться применять их на
практике
4.
Невозможно изучитьновое без повторения
уже изученного
5.
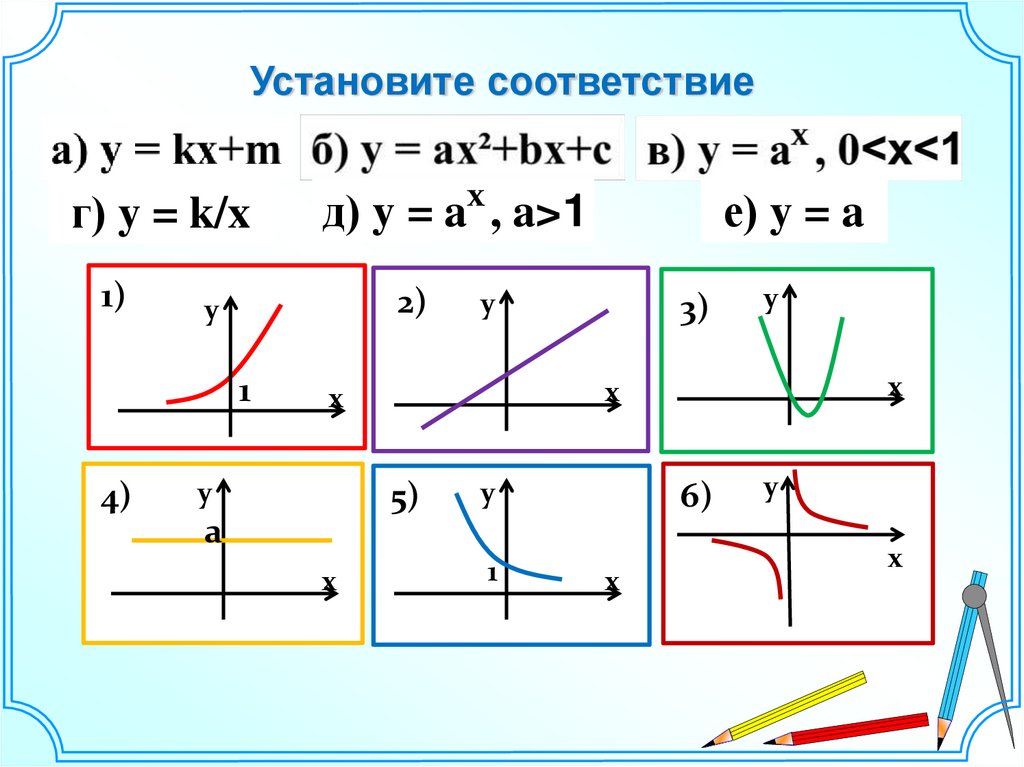
Установите соответствиег) y = k/x
1)
2)
у
1
4)
д) y = ax , a>1
у
3)
5)
у
х
6)
a
х
у
х
х
у
е) y = a
1
х
у
х
6.
Проверьтеа
б
в
г
д
е
2
3
5
6
1
4
7.
Решить уравнения:1) x = 3
2) x = -2/3
3) Корней нет
4)
5) x₁‚₂= ±2
6) ?
8.
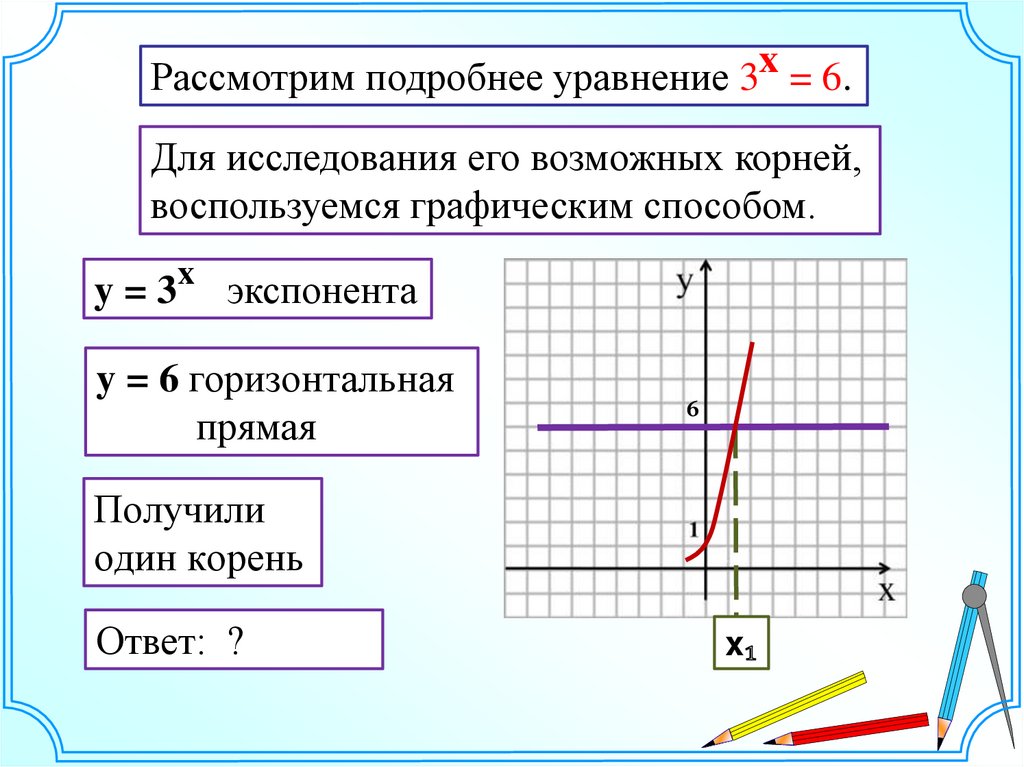
xРассмотрим подробнее уравнение 3 = 6.
Для исследования его возможных корней,
воспользуемся графическим способом.
y=3
x
экспонента
y = 6 горизонтальная
прямая
6
Получили
один корень
Ответ: ?
x₁
9.
Решая последнее уравнение,мы столкнулись с проблемой
записи полученного ответа.
Прежних знаний для этого
явно недостаточно.
Можно оценить корень
1 < x₁ < 2, т.к.
x
3 < 3чxчxx
< 9.
10.
Выводы:• уравнение имеет один корень
• корень – число
(показатель степени числа 3)
Такой вывод можно сделать для
любого уравнения вида
,
где
,
11.
Для корней показательных уравненийиспользуют запись
,
где
- логарифм числа b
по основанию .
x
1) 12 = 5; x = log₁₂ 5
x
2) 4 = 9; x = log₄ 9
3) 0,7 = 0,49; x = log₀‚₇0,49; x = 2
12.
Мы получили новую математическуюмодель – логарифм числа.
Логарифмом числа
по основанию
называется такой показатель степени k,
в который надо возвести , чтобы
получить , т.е. log b = k,
Примеры: log₂16 = 4, т.к. 2⁴ = 16.
log₀‚₃0,09 =2, т.к. 0,3²=0,09
13.
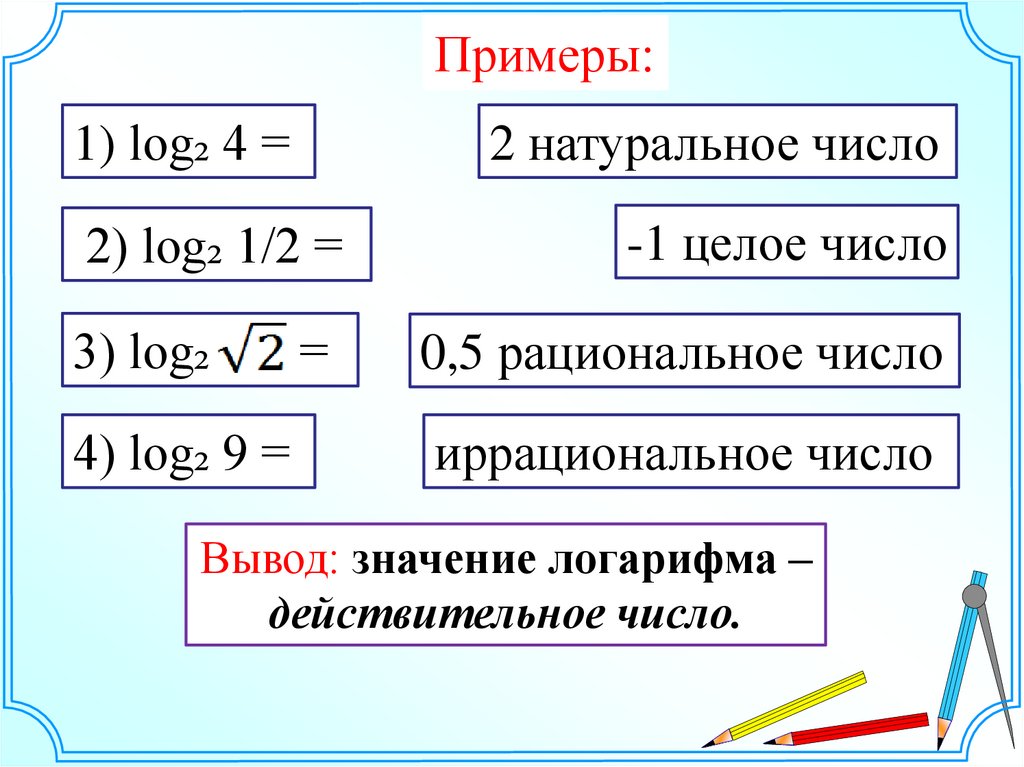
Примеры:1) log₂ 4 =
2 натуральное число
2) log₂ 1/2 =
3) log₂
4) log₂ 9 =
=
-1 целое число
0,5 рациональное число
иррациональное число
Вывод: значение логарифма –
действительное число.
14.
Из определения логарифма следует:a
loga b
b
2 7
x
x log 2 7
2
log2 7
Основное
логарифмическое
тождество
7
3
log3 5
7
log7 10
5
10
log0 , 1 8
8
0 ,1
15.
Из определения логарифма следует:log a a 1;
a a.
log a 1 0;
a 1.
log a a c;
a a .
c
1
0
c
c
16.
Взаимно обратные действия:7 2 49;
log 7 49 2.
10 1000;
log 10 1000 3.
3
5
3
1
;
125
1
log 5
3 .
125
17.
Историческая справкаНа протяжении 16 века быстро возрастало количество
приближенных вычислений, прежде всего, в астрономии.
Совершенствование инструментов, исследование планетных
движений и другие работы потребовали колоссальных, иногда
многолетних, расчетов. Астрономам грозила реальная
опасность утонуть в невыполненных расчетах.
Проблемы возникали и в других областях, например, в
финансовом и страховом деле нужны были таблицы сложных
процентов для различных значений процента.
Главную трудность представляли умножение, деление
многозначных чисел.
18.
Историческая справкаДжон Непер
Логарифмы были придуманы для ускорения и
упрощения вычислений.
Идея логарифма, т. е. идея выражать числа в виде
степени одного и того же основания, принадлежит
Михаилу Штифелю. Но во времена Штифеля
математика была не столь развита и идея логарифма не
нашла своего развития.
Логарифмы были изобретены позже одновременно и
независимо друг от друга шотландским учёным
Джоном Непером(1550-1617) и швейцарцем Иобстом
Бюрги(1552-1632).
В1614г. была опубликована работа Непера под названием «Описание
удивительной таблицы логарифмов»
Слово «логарифм» введено Непером, происходит от греческих
слов logoz и ariumoz - оно означает буквально “числа отношений”.
19.
Ценность логарифмовсостоит в сведении сложных действий возведения в степень и
извлечения корня к более простым действиям - умножению и
делению, а последних к - самым простым – сложению и
вычитанию.
Поэтому открытие логарифмов, сводящее умножение и деление
чисел к сложению и вычитанию их логарифмов упростило жизнь
тех, кто по роду своей деятельности был связан с громоздкими
вычислениями и сложными расчетами.
Палочки Непера
Логарифмическая линейка
20.
Докажите, что:Доказательство:
21.
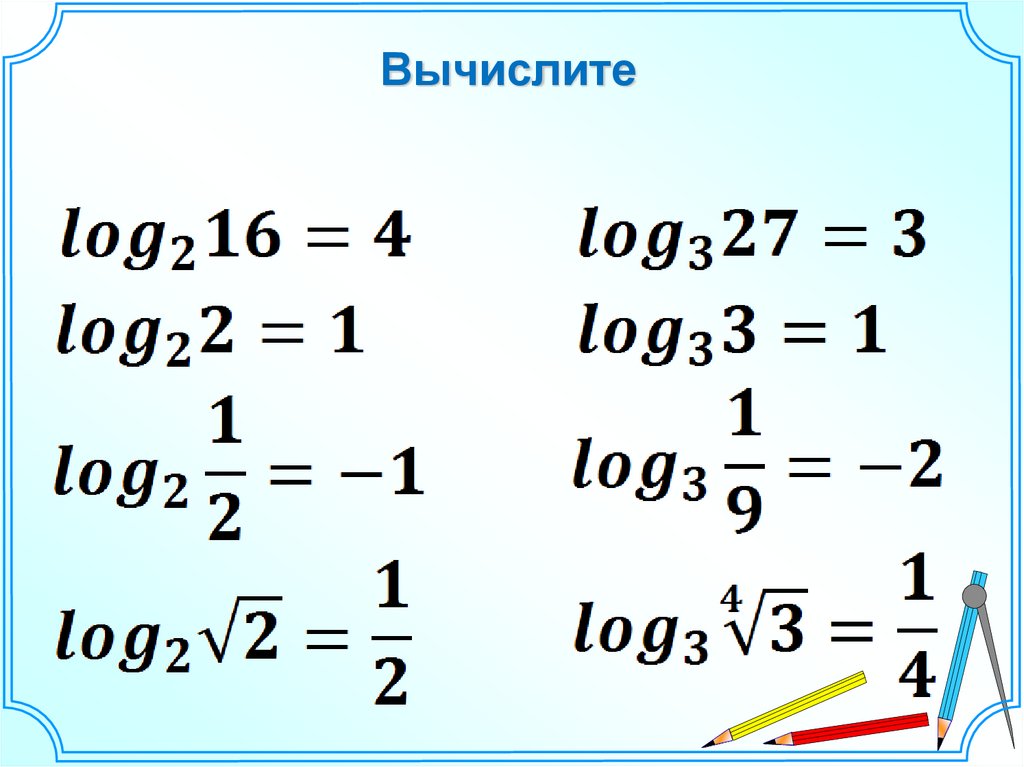
Вычислите22.
Вычислите23.
Оказываетсяматематическим символом соотношения формы и роста
является логарифмическая спираль
раковина моллюска
семена подсолнечника
рога горных баранов
24.
ОказываетсяПо логарифмическим спиралям закручены и многие
галактики, в том числе и Галактика, которой
принадлежит Солнечная система
25.
Домашнее заданиеОтветьте на вопросы:
1. Где встречается понятие логарифма?
2. Для чего нужен логарифм числа в
математике?
3. Действие нахождения логарифма числа
называют…
4. Чему равно основание данного
логарифма?
log 5 25 2
5.Каким числом может быть логарифм?
6. Перечислите имена математиков,
которые внесли новое в изучение
логарифмов.
7.Законспектируйте слайд 20,21.





















 mathematics
mathematics








