Теорія ймовірностей, ймовірнісні процеси і математична статистика

1.

Теорія ймовірностей,
ймовірнісні процеси і
математична статистика
9,10 ПЗ: ВАРІАЦІЙНІ РЯДИ. СТАТИСТИЧНІ ОЦІНКИ:
Тема 1. Характеристики варіаційних рядів.
Тема 2. Точкове та Інтервальне оцінювання.

2.

Тема 1. ВАРІАЦІЙНІ РЯДИ.
Характеристики
варіаційних рядів.

3.

Определение статистического ряда
Обозначим через X - изучаемый признак, через xi наблюдаемые
значения
признака,
i=1,2,...,n
где n - объем изучаемой совокупности (выборки).
Различные значения признака, наблюдающиеся у
элементов совокупности называются вариантами v1, v2 ,
..., vk , а числа, показывающее, сколько раз встречается
каждая варианта называются частотами f1, f2 , ..., fk.
Ясно, что всегда выполняется условие k ≤ n , где k –
количество уникальных значений вариантов.
Статистический ряд распределения - это упорядоченное
распределение единиц совокупности на группы по
определенному варьирующему признаку.

4.

Определение вариационного ряда
Вариационным рядом называется ранжированный
(упорядоченный по возрастанию или убыванию) ряд
вариантов.
Вариационный ряд называется дискретным, если
любые его варианты отличаются на некоторую
величину, и – интервальным (непрерывным), если
варианты могут отличаться один от другого на сколь
угодно малую величину.

5.

Определение вариационного ряда частот
Вариационным
рядом
частот
или
рядом
распределения частот называется ранжированный
ряд вариантов и соответствующих им частот.
Для частот выполняется равенство:
Каждой варианте можно поставить в соответствие не
только частоту, а и одну из следующих величин:
относительную
частоту,
накопленную
частоту,
накопленную относительную частоту, построив при
этом соответствующий вариационный ряд.

6.

Определение относительной частоты
Относительной частотой (частостью) варианта vj
называется отношение его частоты к объему
совокупности, т.е. величина
Относительная частота варианта vj определяет долю
(удельный вес) элементов в совокупности, значения
признака у которых равны значению vj.
Для относительных частот выполняется равенство:

7.

Определение накопленной частоты
Накопленной частотой варианта vj называется
сумма частот всех предшествующих ему вариантов
и частоты данного варианта:
Накопленная частота варианта vj показывает, сколько
элементов
выборочной
совокупности
имеют
значение признака, меньшее или равное значению vj.

8.

Определение накопленной относительной частоты
Накопленной относительной частотой варианта vj
называется сумма относительных частот всех
предшествующих ему вариантов и относительной
частоты данного варианта:
Накопленная относительная частота варианта vj
показывает долю тех элементов совокупности, у
которых значение изучаемого признака меньше или
равно значению этого варианта и может также
определяется как отношение накопленной частоты к
общему числу наблюдений, т.е.

9.

Расчеты для дискретных вариационных рядов

10.

Выбор вида вариационного ряда
Если количество вариантов k слишком велико или близко к объему
выборки, то дискретный вариационный ряд оказывается неудобным для
проведения анализа вариации признака. В этом случае целесообразно
составить вариационный ряд по интервалам значений изучаемого
признака, т.е. интервальный вариационный ряд.
Для построения интервального вариационного ряда весь диапазон
изменения признака, от минимального xmin до максимального xmax,
разбивают на определенное число интервалов (a j , a j+1], j =1,2,...,k.
Затем подсчитывают число элементов совокупности, значения признака
которых попадает в тот или иной интервал, т.е. вычисляют частоты
попаданий значений признака в интервал. Число интервалов, как
правило, выбирают от 7 до 16, так, чтобы в каждый интервал попадало не
менее 5 % всех наблюдений.
Так как некоторые значения признака могут совпадать с границами
интервалов, то в каждый интервал включаются варианты большие, чем
нижняя граница интервала и меньшие или равные верхней границе
интервала. Другими словами, граничное значение следует относить к
интервалу, у которого данное значение является верхней границей.

11.

Расчеты для интервальных вариационных рядов

12.

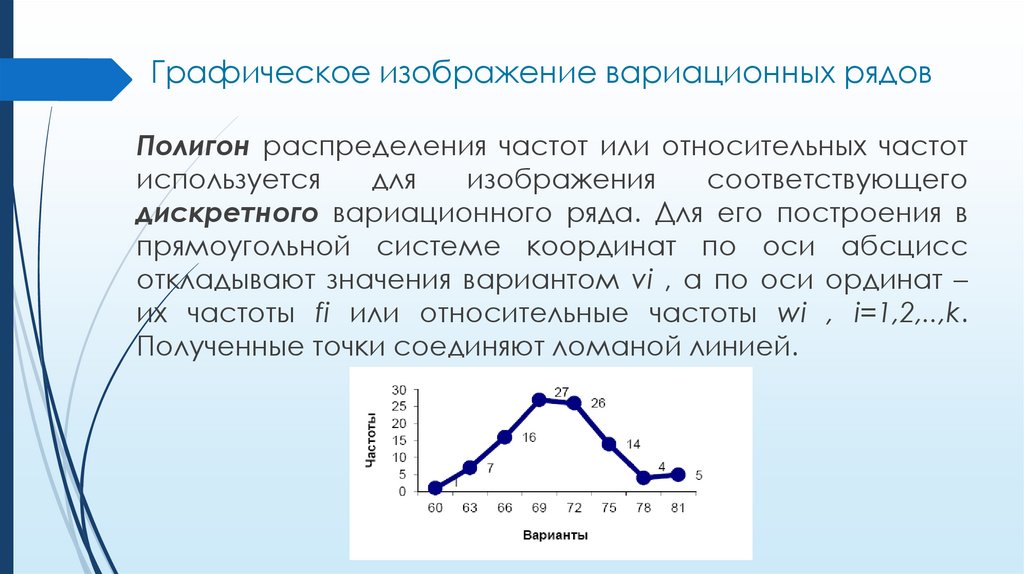
Графическое изображение вариационных рядов
Полигон распределения частот или относительных частот
используется
для
изображения
соответствующего
дискретного вариационного ряда. Для его построения в
прямоугольной системе координат по оси абсцисс
откладывают значения вариантом vi , а по оси ординат –
их частоты fi или относительные частоты wi , i=1,2,..,k.
Полученные точки соединяют ломаной линией.

13.

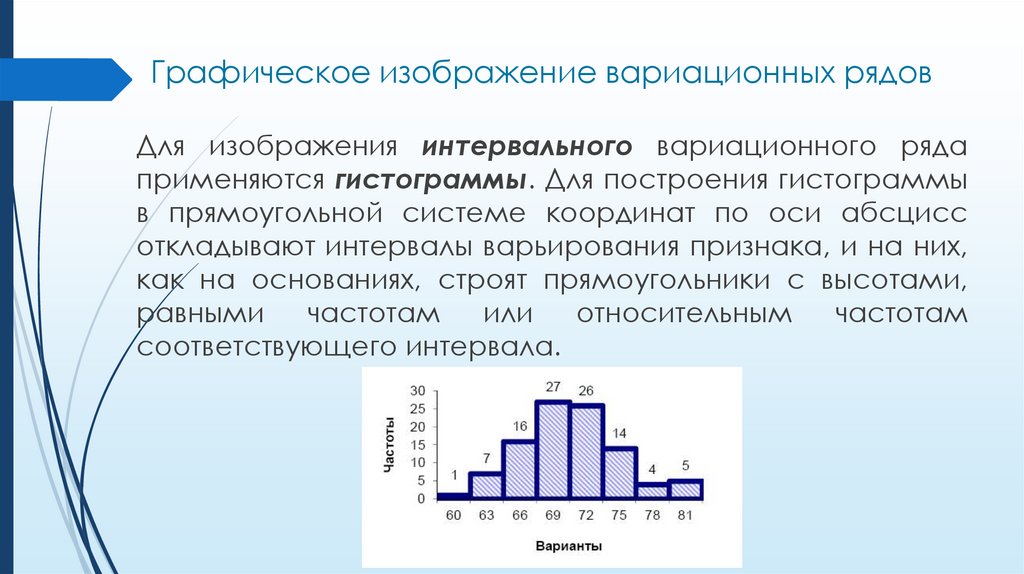
Графическое изображение вариационных рядов
Для изображения интервального вариационного ряда
применяются гистограммы. Для построения гистограммы
в прямоугольной системе координат по оси абсцисс
откладывают интервалы варьирования признака, и на них,
как на основаниях, строят прямоугольники с высотами,
равными
частотам
или
относительным
частотам
соответствующего интервала.

14.

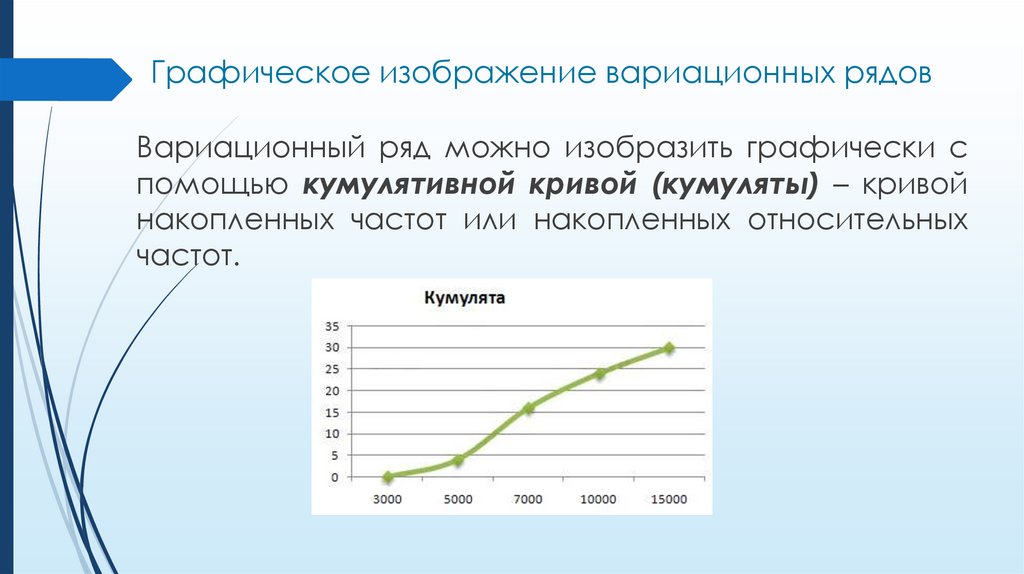
Графическое изображение вариационных рядов
Вариационный ряд можно изобразить графически с
помощью кумулятивной кривой (кумуляты) – кривой
накопленных частот или накопленных относительных
частот.

15.

Числовые характеристики вариационных рядов
Средняя
арифметическая
характеризует
типичный для совокупности размер признака,
т.е. центральную тенденцию в распределении
и вычисляется по формуле
Если
по
наблюдениям
составлен
вариационный ряд, то можно использовать
следующую формулу:

16.

Числовые характеристики вариационных рядов
Модой называется значение признака, которому соответствует
наибольшая частота, т.е. которое наблюдалось наибольшее
число раз.
Для дискретного ряда мода находится непосредственно из
распределения частот.
Если составлен интервальный вариационный ряд, то мода
вычисляется по следующей приближенной формуле:
где x0 – начало модального интервала, т.е. интервала,
имеющего максимальную частоту, h – длина модального
интервала, fj – частота модального интервала, fj-1 и fj+1 –
частоты соответственно предшествующего и последующего за
модальным интервалов.

17.

Числовые характеристики вариационных рядов
Медианой называется значение признака, приходящееся на
середину ранжированного ряда наблюдений.
Пусть результаты наблюдений размещены по возрастанию и
построен производный ряд x’i, i=1,2,..,n.
Если проведено нечетное число наблюдений:
Если проведено четное число наблюдений:
Если составлен интервальный вариационный ряд, то медиана
вычисляется по следующей формуле:

18.

Числовые характеристики вариационных рядов
Средним линейным отклонением называется средняя
арифметическая
абсолютных
величин
отклонений
наблюдаемых
значений
признака
от
средней
арифметической:
Если по наблюдениям
применяют формулу:
построен
вариационный
ряд,
то

19.

Числовые характеристики вариационных рядов
Дисперсией называется средняя арифметическая квадратов
отклонений наблюдаемых значений признака от средней
арифметической:
Если по наблюдениям
применяют формулу:
построен
вариационный
ряд,
то

20.

Числовые характеристики вариационных рядов
При
вычислении
дисперсии
суммируются
квадраты
отклонений вариантов, в силу чего дисперсия измеряется в
квадратах тех единиц, в которых измеряется изучаемый
признак.
Для
того,
чтобы
характеристика
вариации
выражалась в тех же единицах, что и значения признака,
используют корень квадратный из дисперсии.
Средним квадратическим (стандартным) отклонением
называется арифметическое значение корня квадратного из
дисперсии

21.

Числовые характеристики вариационных рядов
Для сравнительной оценки вариации в распределениях с
различными
значениями
средней
используется
также
коэффициент вариации, равный выраженному в процентах
отношению среднего квадратического отклонения к средней
арифметической:
Если V ≤ 33%, то статистическая совокупность является
однородной и средняя будет отражать типичный размер
изучаемого признака. Если коэффициент вариации V > 33%,
то, как правило, можно сделать вывод о неоднородности
статистической совокупности и средняя арифметическая не
является типичным значением для всех элементов.

22.

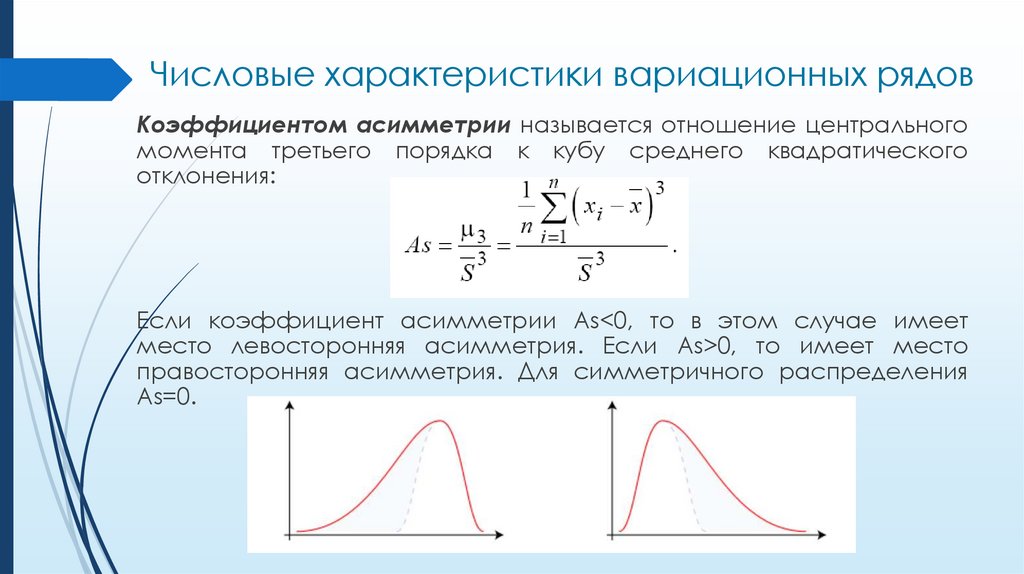
Числовые характеристики вариационных рядов
Коэффициентом асимметрии называется отношение центрального
момента третьего порядка к кубу среднего квадратического
отклонения:
Если коэффициент асимметрии As<0, то в этом случае имеет
место левосторонняя асимметрия. Если As>0, то имеет место
правосторонняя асимметрия. Для симметричного распределения
As=0.

23.

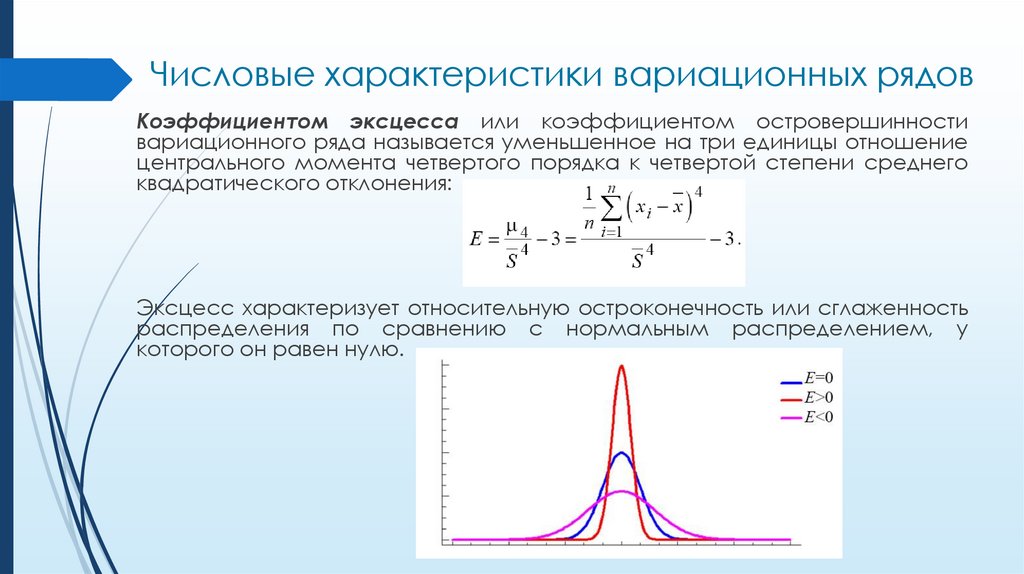
Числовые характеристики вариационных рядов
Коэффициентом эксцесса или коэффициентом островершинности
вариационного ряда называется уменьшенное на три единицы отношение
центрального момента четвертого порядка к четвертой степени среднего
квадратического отклонения:
Эксцесc характеризует относительную остроконечность или сглаженность
распределения по сравнению с нормальным распределением, у
которого он равен нулю.

24.

Тема 2. СТАТИСТИЧНІ ОЦІНКИ.
Точкове та Інтервальне
оцінювання.

25.

Определение доверительного интервала
Генеральные
совокупности
характеризуются
некоторыми
постоянными
числовыми
характеристиками
распределения.
Математическая теория выборочного метода основывается на
анализе случайной выборки, по которой можно найти оценки этих
характеристик.
Чтобы оценить параметр генеральной совокупности достаточно
оценить его в выборке. Статистической оценкой при этом и будет
оценка параметра генеральной совокупности в каком-то
интервале, который называется доверительным.
Доверительным интервалом или интервальной оценкой параметра
генеральной совокупности называется интервал, который содержит в
себе значение параметра с заданной, близкой к единице
доверительной вероятностью (надежностью). При этом чем больше
вероятность - тем меньше ошибка.

26.

Доверительный интервал для генеральной средней
Пусть количественный признак X генеральной совокупности
распределен по нормальному закону XєN(μ,σ), причем значение
среднего квадратического отклонения σ неизвестно. Требуется
оценить неизвестное значение генеральной средней μ по
выборочной средней x.
Доверительный интервал, включающий в себя генеральную
среднюю μ с надежностью ɣ , определяется из условия:
где x – выборочная средняя; S – исправленное выборочное среднее
квадратическое (стандартное) отклонение, n – объем выборки; ɣ –
доверительная вероятность; = (1 – ɣ) – уровень значимости; t ;k –
значение случайной величины, которая имеет распределение
Стьюдента (t-распределение) с числом степеней свободы k = n-1 и
определяются по таблице t-распределения Стьюдента.

27.

Доверительный интервал для генеральной дисперсии
Пусть количественный признак X генеральной совокупности
распределен по нормальному закону и по выборке объема n
определены выборочная средняя x, исправленные дисперсия S2 и
среднее квадратическое отклонение S.
Доверительный интервал, включающий в себя
дисперсию σ2 с надежностью ɣ определяет условие:
генеральную
где n – объем выборки; S2 – исправленная выборочная дисперсия; χ2
– значения случайной величины , которая имеет распределение
Пирсона с числом степеней свободы k=n–1, принимает только
неотрицательные значения и определяется по таблице χ2 –
распределения в соответствии с уровнем значимости
и числом
степеней свободы k=n–1.

28.

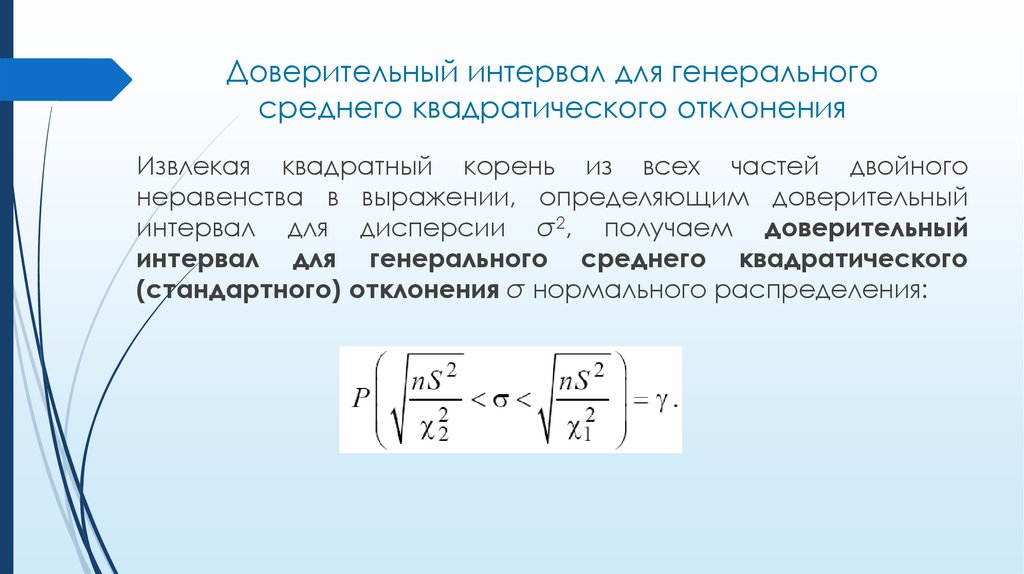
Доверительный интервал для генерального
среднего квадратического отклонения
Извлекая квадратный корень из всех частей двойного
неравенства в выражении, определяющим доверительный
интервал для дисперсии σ2, получаем доверительный
интервал для генерального среднего квадратического
(стандартного) отклонения σ нормального распределения:

29.

Задание
Самостоятельное решение типовых заданий с учетом вариантов
средствами Excel и записью вручную только конечных формул с
числовой подстановкой
3 типовые задачи (Тема 9)
1 типовая задача (Тема 10)
Решение индивидуальных задач вручную
10 инд. задач (Тема 10)
Контрольная работа по
следующем пз (3-4 задачи)
задачам
всех
пройденных
тем
на