Similar presentations:
Определение первообразной
1. Определение первообразной
2. План урока
1. Анализ контрольной работы.2.Повторение материала,
необходимого для изучения
новой темы.
3. Изучение нового материала.
4. Закрепление нового
материала.
5.Проверка изученного.
6. Итог урока.
3. ЗАДАНИЕ
1.Слайд№ 4.Повторить правиланахождения производных, 1 курс. Устно
вычислить производные
2.Записать определение, слайд№12,
пример, слайд №13
3.Решить, слайд№14
4. Найти производную
1. у = 52. у = 10х
3. у = х25
4. у = х30 - 7
5. у = х4 + sinx
6. у = 10х + cos x
7. у = х5 + 25
8. у = 5х2
(х)' = 1,
(С)' = 0.
( хn )' = n · хn-1
5.
ХVIII век часто называютвеком научной революции,
определившей развитие
общества вплоть до наших
дней. Базировалась эта
революция на замечательных
математических открытиях,
совершенных в ХVII веке и
осознанных в последующее
столетие
6.
Нет ни одного объекта в материальноммире и ни одной мысли в области духа , на
которых не отразилось бы влияние
научной революции ХVIII. Ни один
элемент современной цивилизации не мог
бы существовать без принципов механики,
без аналитической геометрии,
дифференциального и «интегрального
исчисления. Нет ни одной отрасли в
деятельности человека, которая не
испытала бы на себе влияние гения
Галилея, Декарта, Ньютона и Лейбница».
( фр. матем. Э. Борель (1871-1956г.))
7.
8.
9.
10.
ЧебышевРусский математик.
Его исследования
относятся к теории
приближения
функций многочленами.
11. Вспомним механику
Известно ускорение точки а(t)(в нашем случае оно постоянно),
требуется найти закон изменения
скорости, а затем найти координату
S(t). Иными словами, по заданной
производной, равной а(t), нужно найти
скорость, а затем и координату. Для
решения таких задач служит операция
интегрирования, обратная
дифференцированию
12. Вспомним механику
Определение: Функция Fназывается первообразной для f на
заданном промежутке, если для всех
х из этого промежутка выполнено:
F'(х) = f (х)
13. Пример.
3x
F x
первообразная
3
для
f x x
2
14.
Найдите функцию f(х) для F(х)(пример на следующем слайде)
1. F(х) = х5
2. F(х) = х-3,
3. F(х) = х6,
4. F(х) = 3 - 2sin x,
5. F(х) = cosx – 5х,
6. F(х) = 10 - х4,
15. Пример
1.F(х) = х5f′(х)= F′(х) =(х5)′=5х4
Дифференцируем по формуле
( хn )' = n · хn-1, подставляя вместо n = 5
16.
7. F(х) = х6 + 2х,8. F(х) = х-30,
9. F(х) = 5х4 - 4х2,
10. F(х) = 5 - sin x,
11. F(х) = cosx - 4,
12. F(х) = 5 – х5,
17.
Проверьтесамостоятельно,
является ли функция F
первообразной для f .
18.
1 вариант.1. F(х) = х3, для f(х) = 3х2 ;
2. F(х) = х-4, для f(х) = -4х-5 ;
3. F(х) = х6 + 3х, для f(х) = 6х5 +3;
4. F(х) = 5 – 10sin x, для f(х) = -10cosx;
5. F(х) = cosx – 7х, для f(х) = -sin x - 7;
2 вариант.
1. F(х) = х5 + 2х + 3, для f(х) = 5х4+2 ;
2. F(х) = х-20, для f(х) = -20х-21 ;
3. F(х) = 4х4 - 5х2, для f(х) = 16х3- 10х;
4. F(х) = 5х - sin x, для f(х) = 5 - cosx;
5. F(х) = cosx - 3, для f(х) = -sin x;
19. Вопросы для закрепления.
1. Что называют первообразной?2. Докажите, что F(х) = 5х, есть
первообразная для f(х) = 5.
3. Докажите, что F(х) = х, есть
первообразная для f(х) = 1.
4. Докажите, что F(х) = sinх, есть
первообразная для f(х) = cos x.















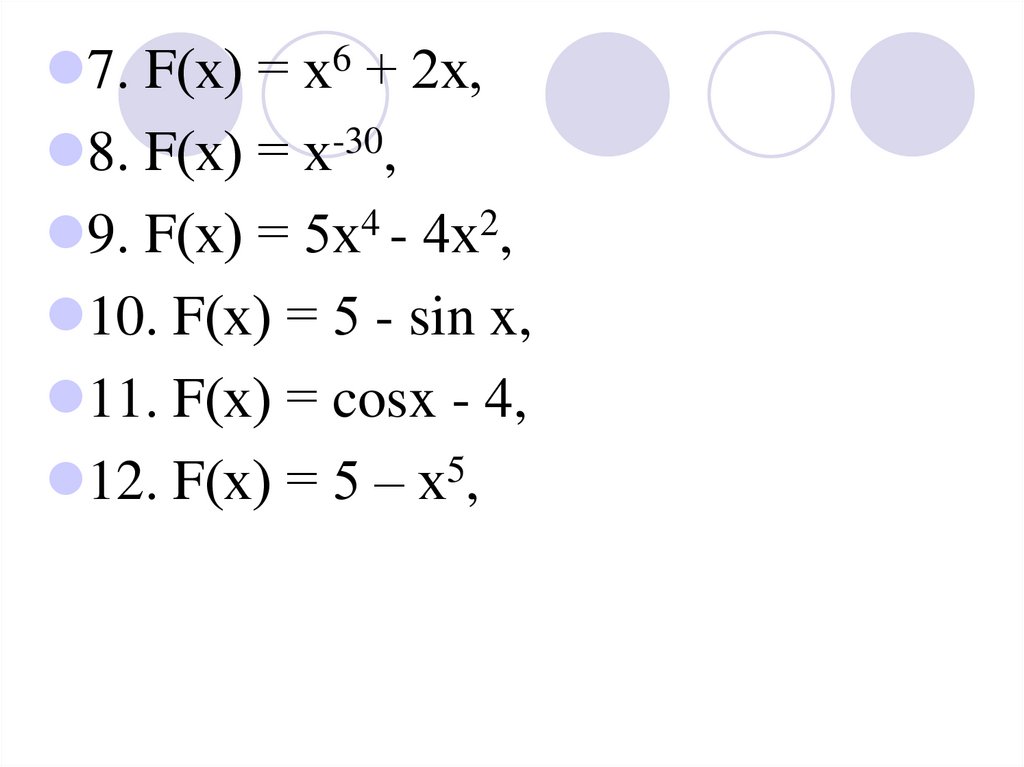




 mathematics
mathematics