Similar presentations:
Моделирование фазовых систем. Тройные взаимные системы
1. Моделирование фазовых систем
3. Тройные взаимные системы2.
T АХT3
AX + BY = AY + BX
T AY
T2
e 4'
T1
T BХ
T BY
e 1'
e 2'
e '3
T
E2
'
'
AY
e4
E1
T3
y
AX
T2
e3
E2
T1
e
e1
E1
BY
e2
x
BX
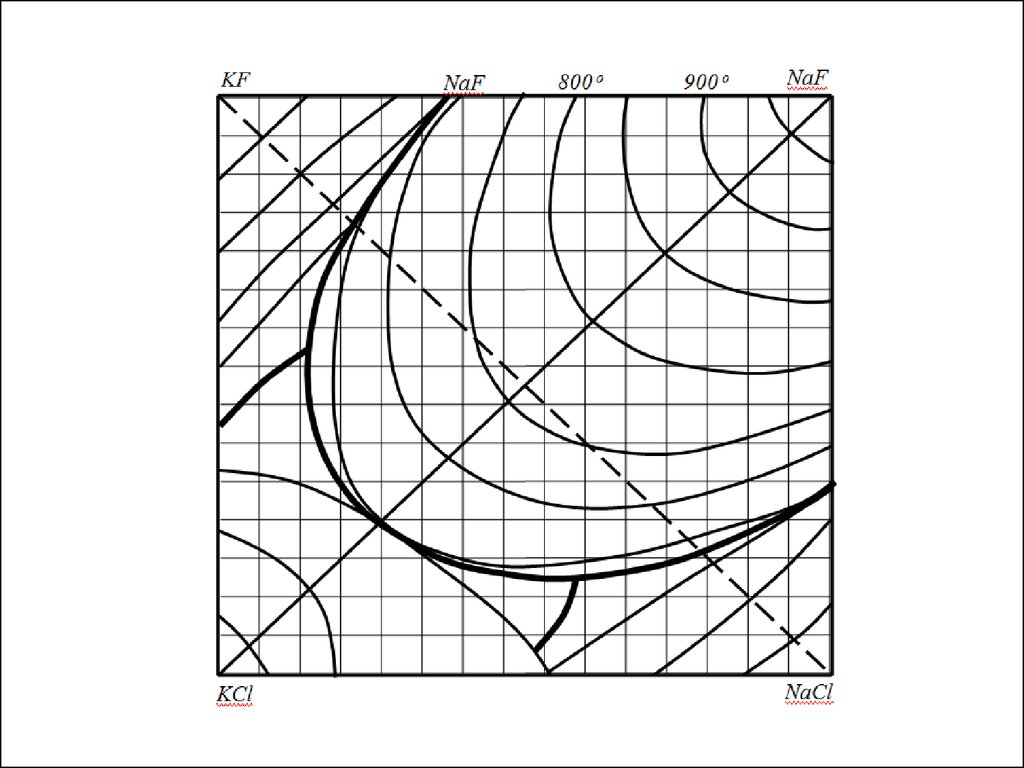
Поверхность первичной кристаллизации системы:
тройные точки, пограничные кривые, поля
кристаллизации соответствующих солей
3.
4. Математические модели фазовых равновесий тройных взаимных систем
• Отличие от двойных систем – наличиеизотерм кристаллизации
• на квадрате составов легко ввести
прямоугольную систему координат.
• присутствует химическая составляющая –
реакция обменного взаимодействия с ее
энергией Гиббса .
5. Вывод уравнения связи для ТВС
• Принимая за стандартное состояние чистую расплавленную соль притемпературе равновесия, получили равенство относительных
потенциалов, которое можно представить в виде
RT ln x y AX Z AX
6. Поверхность первичной кристаллизации соли AX
Подставляя в уравнение выражение для коэффициентовактивности, и выполнив преобразования, получим
изотермический подход позволил из самых общих предпосылок получить
уравнение связи, не содержащее дифференциалов!
7.
условие симметричности изотерм кристаллизацииприводит к тому, что из общего уравнения
«исчезли» все коэффициенты активности. Для
соли уравнение симметричных изотерм имеет
вид:
RT ln xy G (1 x)(1 y ) Z AX 0
ln xy
G
RT
(1 x)(1 y)
Z AX
RT
0
8.
ln (1 x)(1 y)ln (1 x) y
ln x (1 y)
G
RT
G
RT
G
xy
Z BY
x (1 y)
Z BX
RT
(1 x) y
RT
RT
Z AY
RT
0
0
0
9. Возможности полученных уравнений
• вывод и анализ аналитических и геометрическихмоделей фазовых равновесий и состояний ТВС и их
применение для расчета диаграмм плавкости ТВС
по термодинамическим данным;
• расчет термодинамических характеристик систем и
их компонентов по экспериментальным данным о
диаграммах плавкости ТВС;
• получение общей картины взаимосвязи
термодинамических характеристик ТВС с
параметрами их фазовых равновесий и состояний
(параметрический дизайн фазовых состояний и
равновесий ТВС).
10. Виды параметрического дизайна
• параметрических условий первичной кристаллизацииодной твердой фазы и, следовательно, параметрических
критериев существования на диаграмме ТВС полей
кристаллизации соответствующей фазы;
• параметрических условий совместной кристаллизации
двух твердых фаз (параметрических критериев
существования в ТВС соответствующей пограничной
кривой и, в частности, кривых совместной кристаллизации
взаимных пар солей, а также параметрических условий
стабильности и нестабильности диагональных сечений
ТВС);
• параметрических условий совместной кристаллизации
трех твердых фаз (параметрических критериев
существования в ТВС соответствующих тройных точек);
• параметрических условий совместной кристаллизации в
ТВС четырех твердых фаз (условия появления в ТВС точки
конверсии).
11. Условия первичной кристаллизации соли АХ из расплавов ТВС
• 1) Исходя из моделей соответствующих равновесий,следует, что необходимым и достаточным условиями
равновесия с расплавом состава ТВС твердой фазы,
например, соли при температуре и условием отсутствия
подобных равновесий с этим расплавом других солей
является выполнение системы из одного уравнения и трех
неравенств:
RT ln xy G (1 x) (1 y ) Z AX ,
RT ln (1 x) (1 y ) G xy Z ,
BY
RT ln x (1 y ) G (1 x) y Z AY ,
RT ln (1 x) y G x (1 y ) Z BX .
12.
• Система может быть сведена к системе сменьшим числом неравенств.
1) при почленном сложении неравенств одного
знака новое неравенство будет иметь тот же
знак,
2) при почленном вычитании двух неравенств
различного знака сохраняется знак того
неравенства, из которого производится
вычитание.
3) При других вариантах сложения или
вычитания неравенств знак получаемых
неравенств предсказать нельзя.
13.
суммируя почленно три неравенствавыражения получим более простое
условие первичной кристаллизации из
расплава ТВС соли в виде системы из
одного уравнения и одного неравенства:
RT ln x1 y1 G (1 x1 )(1 y1 ) Z AX ,
RT ln (1 x1 y1 ) G (3 y1 x1 y1 ) Z BY Z AY Z BX .
14.
• Вычитая из равенства системы егонеравенство, получим условие в виде
одного неравенства
2 G x1 y1 Z AX ( Z BY Z AY Z BX )
• Для точки на диагональном сечении AX-BY
(x=y)
2 G x12 Z AX ( Z BY Z AY Z BX )
• Для х=у=0,5
0,5 G Z AX ( Z BY Z AY Z BX )
15. ЛИНЕАРИЗАЦИЯ ИЗОТЕРМ И РАСЧЕТ ТЕРМОДИНАМИЧЕСКИХ ХАРАКТЕРИСТИК ТРОЙНЫХ ВЗАИМНЫХ СИСТЕМ
ln xyG
RT
(1 x)(1 y)
Z AX
RT
0
u ln xy ,
v (1 x) (1 y)
u
G
RT
v
Z AX
RT
16. Расчет термодинамических характеристик по изотермам кристаллизации солей тройных взаимных систем
17.
G u Г u В ln x Г ln xВ2RT
vВ
(1 x В ) 2
Z AX
u Г ln x Г
RT
18.
19.
Т=7000,000
0,000
-0,500
-1,000
0,200
0,400
y = -3,0241x - 1,1904
R2 = 0,9846
u
-1,500
-2,000
-2,500
-3,000
-3,500
v
0,600
0,800



















 chemistry
chemistry








