Similar presentations:
Определение синуса, косинуса и тангенса угла
1.
Определение синуса, косинусаи тангенса угла
2.
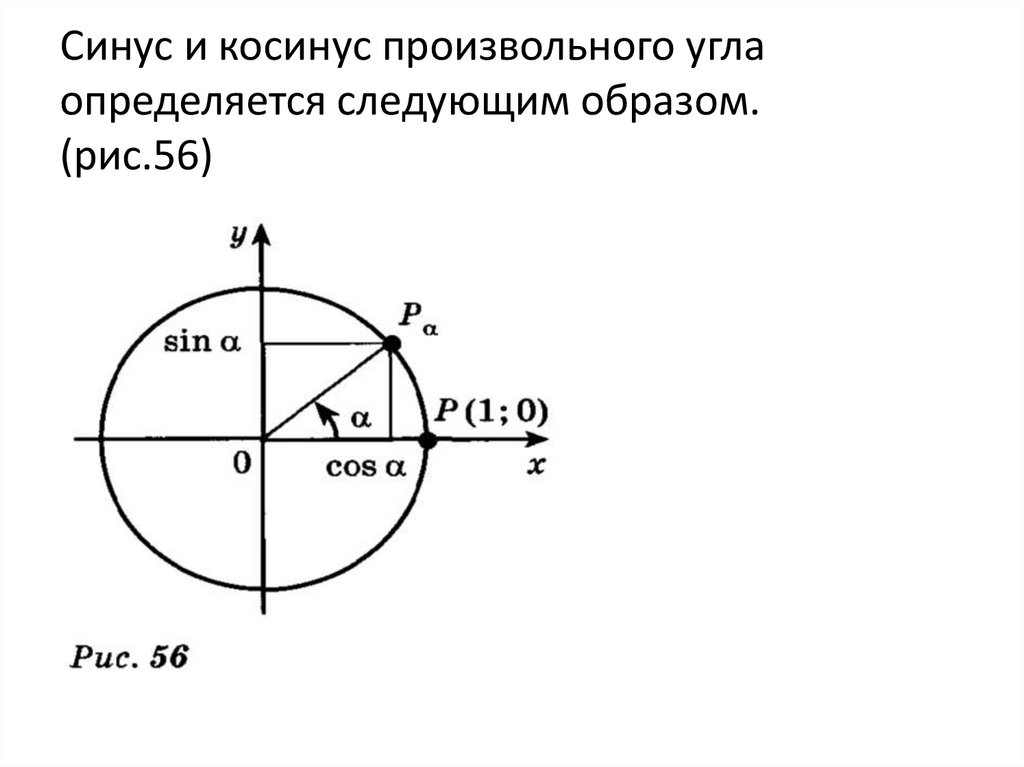
Синус и косинус произвольного углаопределяется следующим образом.
(рис.56)
3.
Определение 1. Синус угла а называетсяордината точки, получиной поворотом точки
(1;0) вокруг начала координат на углу а (
обозначается sin a )
Определение 2. Косинусом угла а называется
абсцисса точки, получиной поворотом точки
(1;0) вокруг начала координат на углу а
(обозначается cos a)
В этих опред. угол а может выражаться как
в градусах, так и в рад.
4.
• Например, при повороте точки (1;0) на угол2/π, т.е угол 90°, получается точка
(0;1). Родина точки (0;1) = 1, поэтому sin π/2 =
sin90° =1; абсцисса этой точки равна 0,
поэтому cos π/2 = cos 90° = 0
Заметим что приведенные определения sin и
cos в случае, когда угол заключён в
промежутке от 0° до 180°, совподаюьт с
определенияси sin и cos, известеными из
курса геометрии.
Например sin π/6 = sin 30° = 1/2,
Cos π = cos 180° = -1
5.
6.
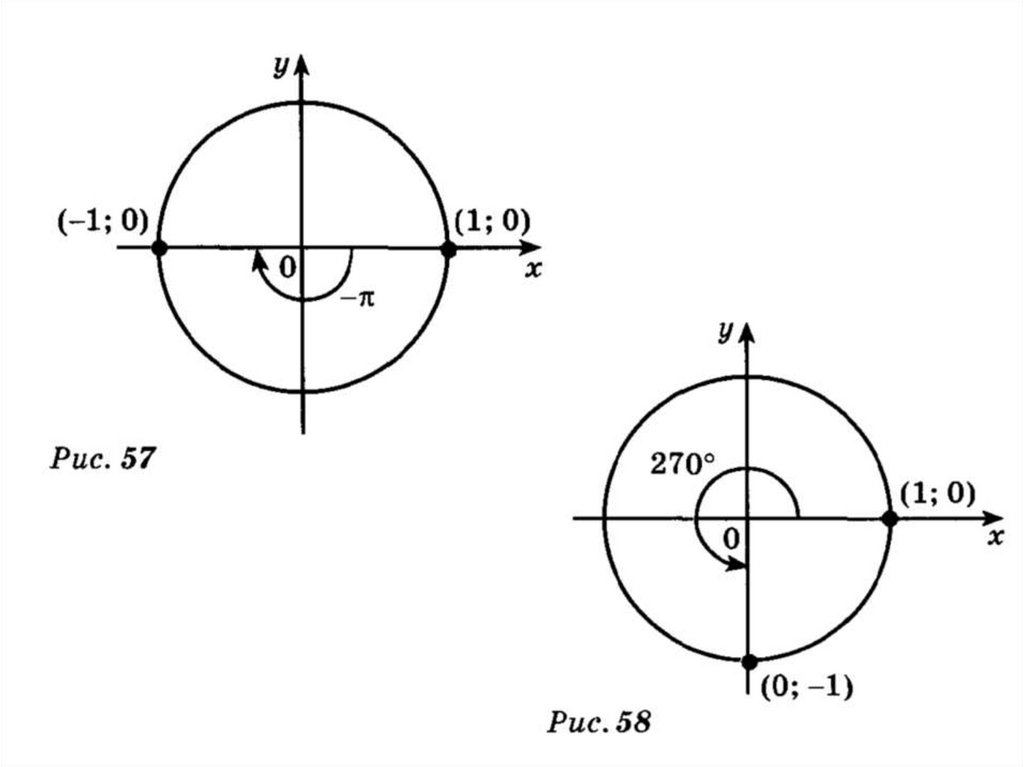
Задача 1 найтиsin (-π) и cos (-π ).Точка (1;0) при повороте на угол -π перейдёт в
точку (-1;0) (рис. 57). Следовательно, sin (-π) = 0,
cos (-π) = -1
Ч.Т.Д.
Задача 2 точка(1;0) при повороте на угол 270°
перейдёт в точку (0; -1) ( рис. 58). Следовательно,
cos 270° = 0, sin 270° = -1.
ЧТД
Задача 3 решить уравнение sin x = 0
Решить уравнение sin x = 0 -это значит найти все
углы, sin которых =0. Ординату, =0, имеют две
точки единичной окружности (1;0) и (-1;0) (рис.
7.
Эти точки получаются из точки (1;0)поворотом науглы 0, π, 2π, 3π и т.д., а также с противоположным
знаком. Следовательно, sinx =0 при х = πК , где К
- любое целое число
ЧТД
а
0
(0°)
Sin a 0
π/6
π/4
π/3
π/2
π
3/2• 2π
(30°) (45°) (60°) (90°) (180° π
(360°
)
(270° )
)
√2/2
√3/2
1
0
-1
0
1/2
Cos a 1
√3/2
√2/2
1/2
0
tg a
1/√3
1
√3
Не
0
существ
ует
0
-1
0
1
Не
0
существ
ует






 mathematics
mathematics








