Similar presentations:
Мультимедийный урок «Параллелепипед»
1.
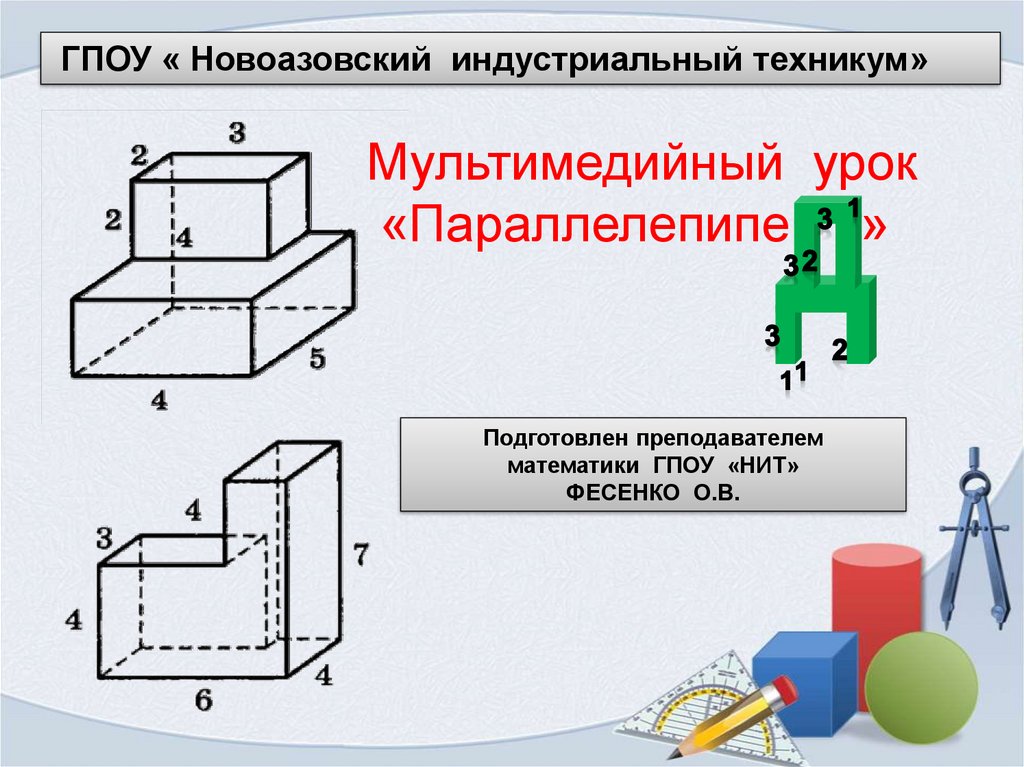
ГПОУ « Новоазовский индустриальный техникум»Мультимедийный урок
«Параллелепипе »
Подготовлен преподавателем
математики ГПОУ «НИТ»
ФЕСЕНКО О.В.
2.
Цели:1. Расширить круг знании о видах
параллелепипедов и их свойствах,
учить применять эти знания при
решении задач
2. Формирование навыков
исследовательской деятельности;
развитие познавательного интереса,
внимания и наблюдательности.
3. Воспитывать стремление к
совершенствованию знаний,
алгоритмическую культуру, интерес к
предмету, трудолюбие.
3. План работы
1. Подготовительный этап (просмотреть слайды 4-9)1. Решение задач на нахождение элементов параллелепипеда
(слайды 10-18)
- изучить образец записи решения задачи (слайд 10);
- разобрать и оформить по образцу решения
задач 1-3 (слайды 11-13);
- разобрать решения задач 4-5, записать только решения
(кратко) (слайды 14-15);
3. Выполнить самостоятельную работу ( слайды16-18)
P. S. На проверку предоставить
самостоятельную работу (три задачи)
до 10 ноября
4.
Вот кирпич, учебник новый,Пастила, журналов тюк.
Назови их форму словом
Из четырнадцати букв!
(Параллелепипед)
5. Виды параллелепипеда
Наклонныйпараллелепипед - это
параллелепипед, боковые
рёбра которого не
перпендикулярны
основаниям.
Прямой
параллелепипед - это
параллелепипед, боковые
грани которого
прямоугольники, а основания
- параллелограммы
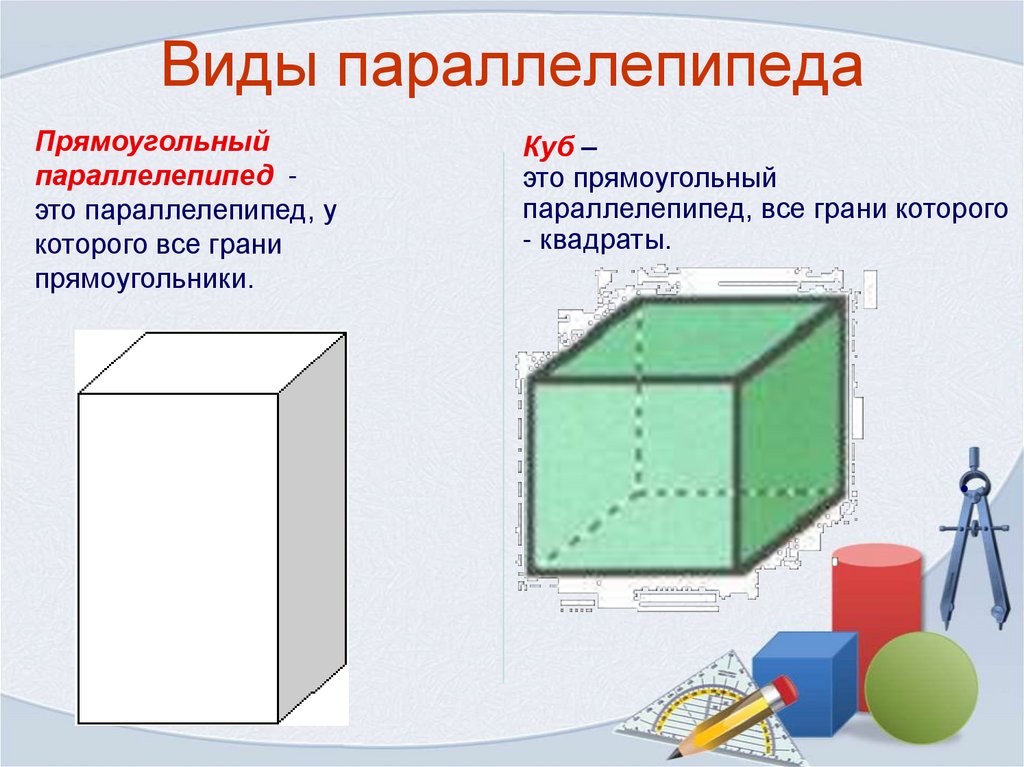
6. Виды параллелепипеда
Прямоугольныйпараллелепипед это параллелепипед, у
которого все грани
прямоугольники.
Куб –
это прямоугольный
параллелепипед, все грани которого
- квадраты.
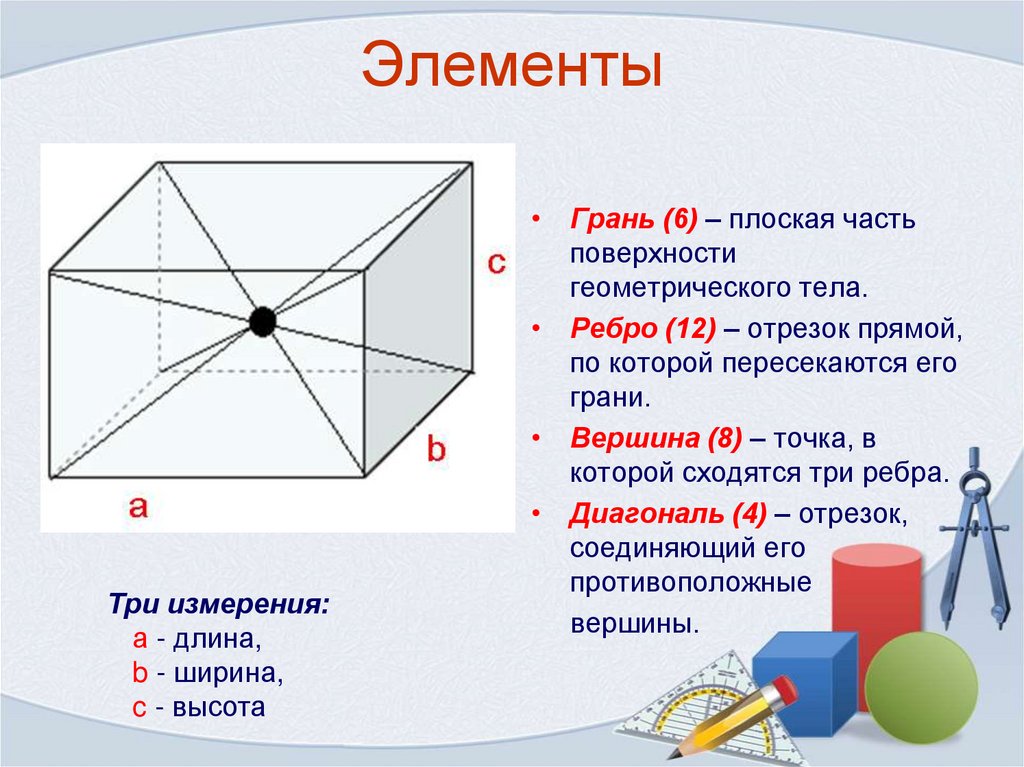
7. Элементы
Три измерения:а - длина,
b - ширина,
c - высота
• Грань (6) – плоская часть
поверхности
геометрического тела.
• Ребро (12) – отрезок прямой,
по которой пересекаются его
грани.
• Вершина (8) – точка, в
которой сходятся три ребра.
• Диагональ (4) – отрезок,
соединяющий его
противоположные
вершины.
8.
9.
Формулы полной поверхности и объёмапрямоугольного параллелепипеда
Sпов. 2(ab bc ac)
V a b c
V S осн h
c
d
b
a
Sпов. Sбок. 2Sосн.
Sбок. Pосн.h
10.
ЗадачаДан прямоугольный параллелепипед АВСDA1B1C1D1.
AB = 4, AD = 6, AA1= 5
Найти диагонали параллелепипеда.
ОБРАЗЕЦ ОФОРМЛЕНИЯ РЕШЕНИЯ ЗАДАЧИ
Дано
АВСDA1B1C1D1 - прямоугольный
параллелепипед,
AB = 4, AD = 6, AA1= 5
Найти BD1.
Решение
1) ∆ ADB – прямоугольный, т.к. < A = 90°.
По т. Пифагора: BD2 = AB2+AD2
BD2 = 42 + 62 = 16 + 36 = 52;
2) ∆ BDD1 - прямоугольный, т.к. < D = 90°. В
По т. Пифагора: BD12 = 52 + 25 = 77.
Ответ. 77
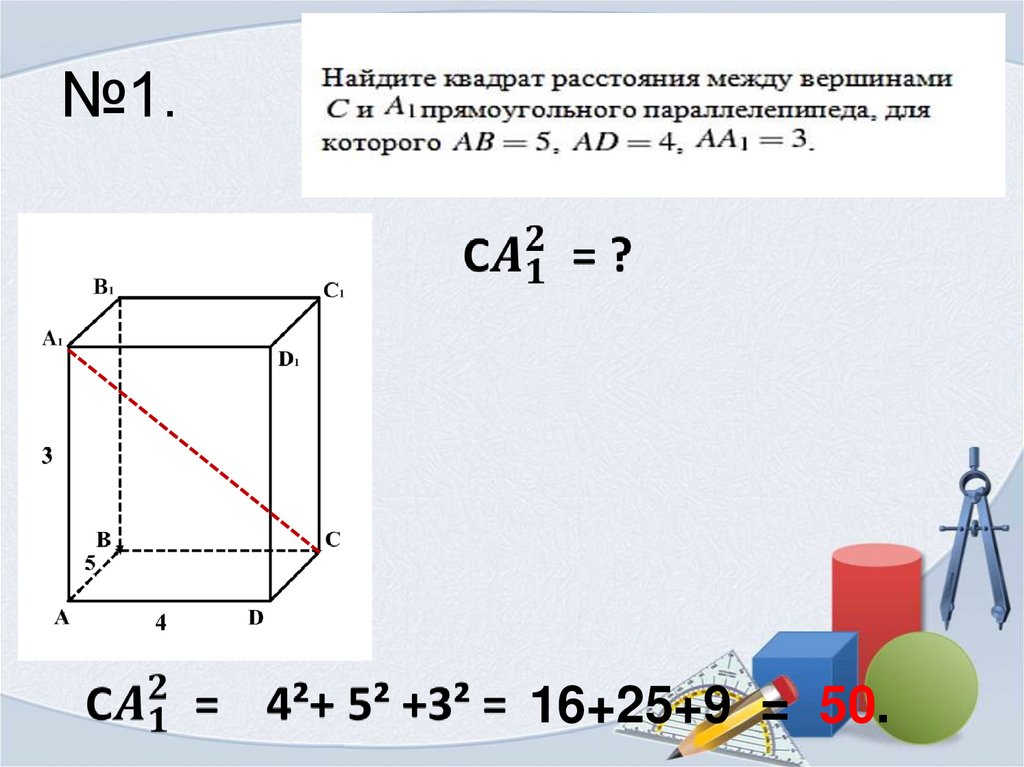
11. №1.
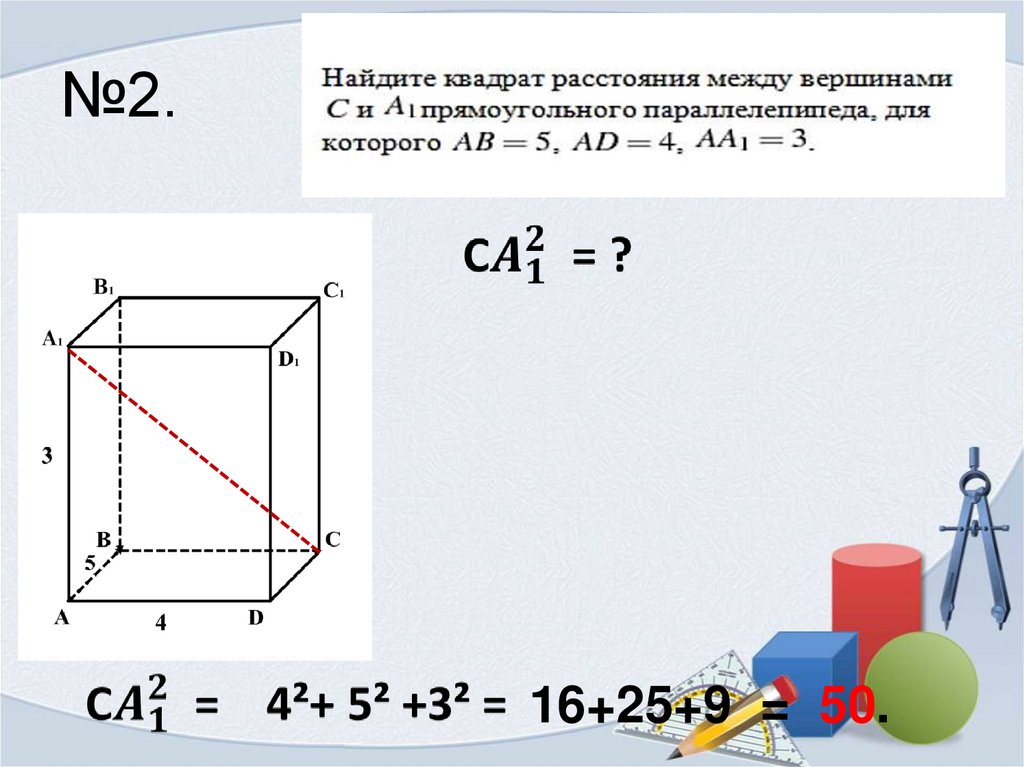
16+25+9 = 50.12. №2.
16+25+9 = 50.13. №3.
D = 90°14.
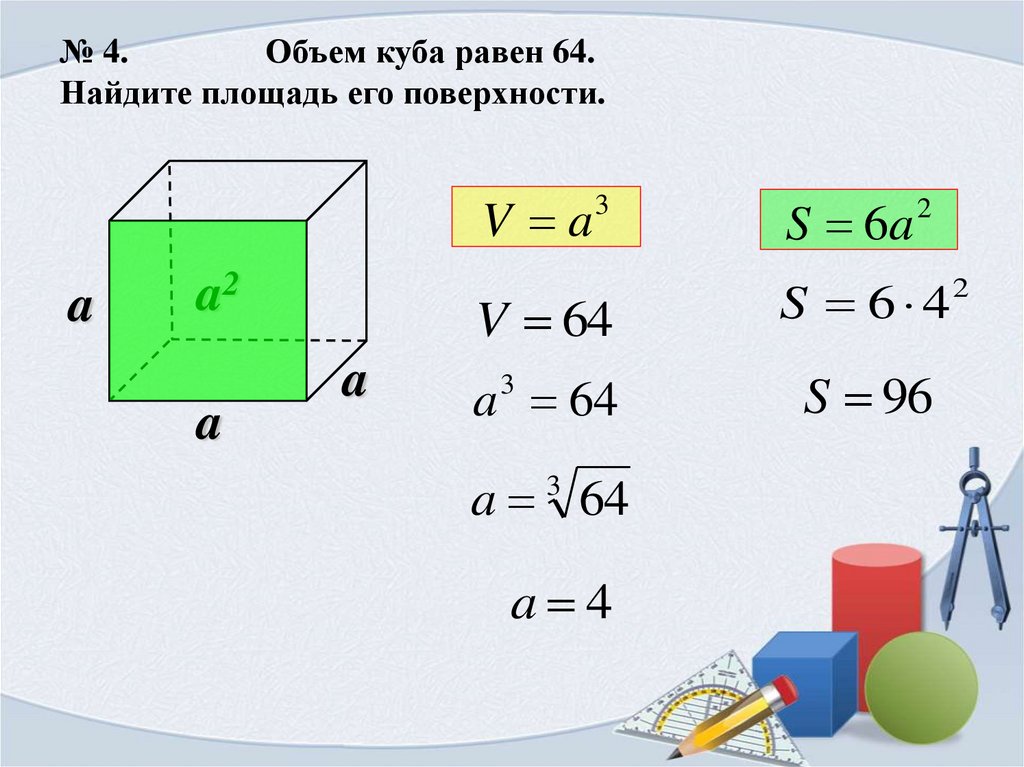
№ 4.Объем куба равен 64.
Найдите площадь его поверхности.
V a
a
a2
a
a
3
S 6a
2
V 64
S 6 4
a 64
S 96
3
a 3 64
a 4
2
15.
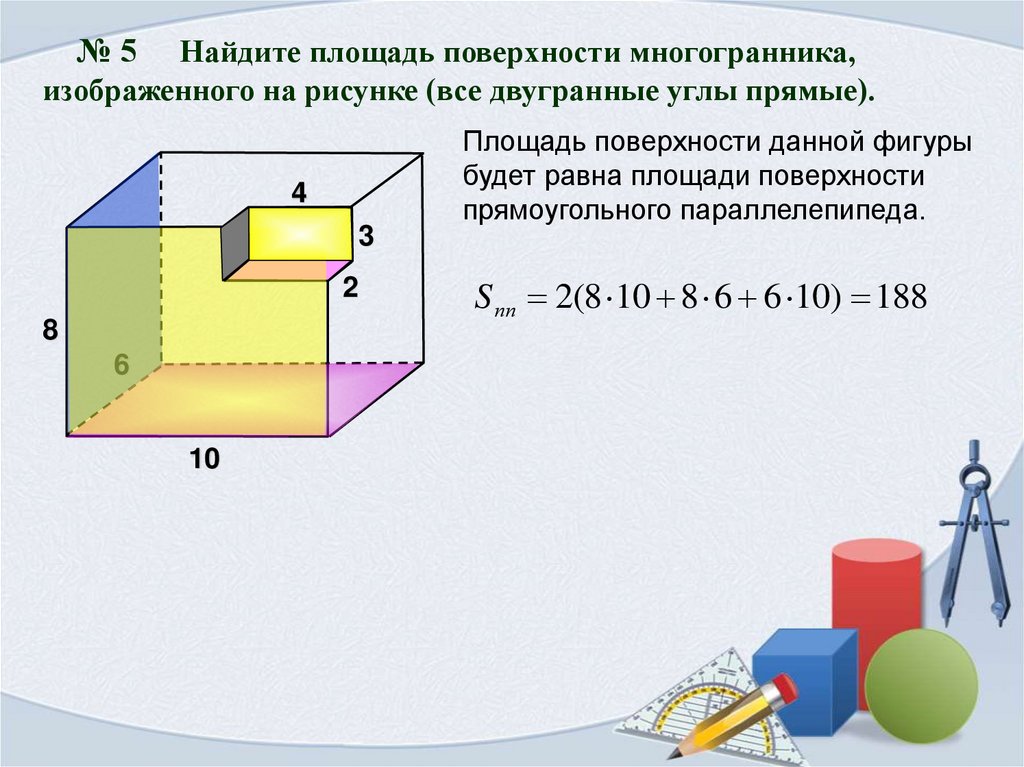
№5Найдите площадь поверхности многогранника,
изображенного на рисунке (все двугранные углы прямые).
4
3
2
8
6
10
Площадь поверхности данной фигуры
будет равна площади поверхности
прямоугольного параллелепипеда.
S пп 2(8 10 8 6 6 10) 188
16.
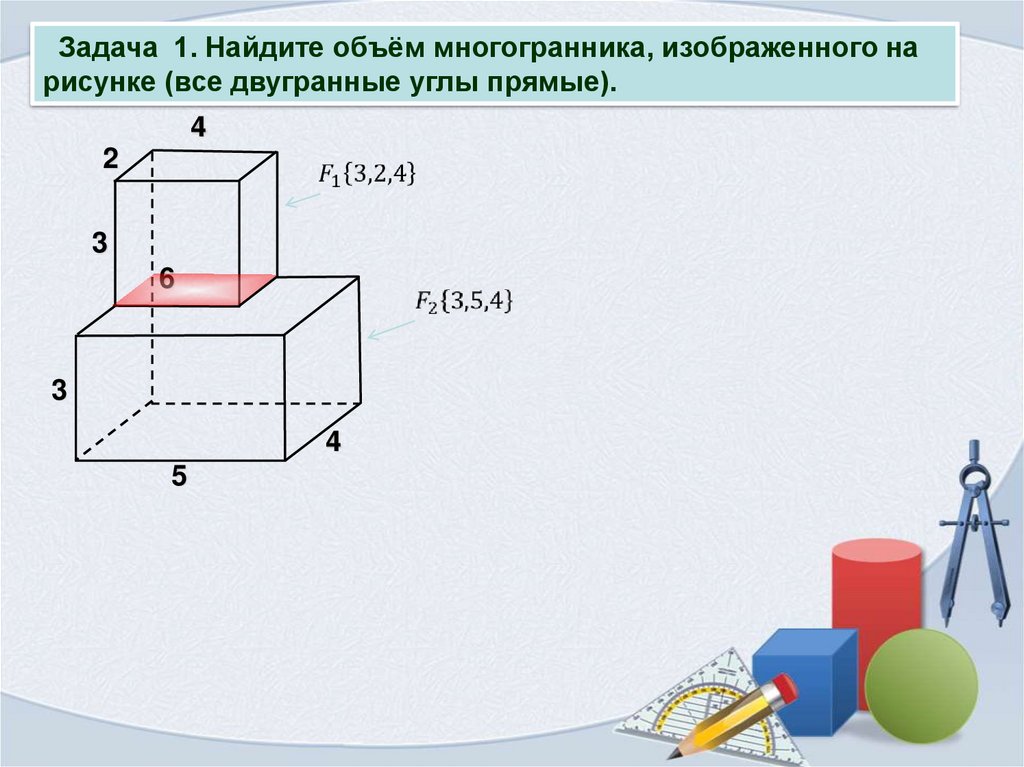
Задача 1. Найдите объём многогранника, изображенного нарисунке (все двугранные углы прямые).
4
2
3
6
3
4
5
17.
Задача 2.Условимся боковые грани куба обозначать буквой Б,
верхнюю — В, нижнюю — Н. Расставьте на
развёртках куба буквы в соответствии с уже
намеченными.
18.
Задача №3 Найдите площадь полной поверхностипрямоугольного параллелепипеда, а = 2, b=4, d =6
c
d
b
a










 mathematics
mathematics








