Similar presentations:
Логарифмический вычет
1. §19.Логарифмический вычет.
Пустьf z C
g \ z1 , , z M
z p - полюса, f g 0
Тогда
g – правильная и
f g
2.
f zОпределение. Функция z
f z
'
называется логарифмической
производной функции f(z).
Выч[ (z), zk ] называются
логарифмическими вычетами
zk : zn -нули f(z) и zз -полюса f(z) .
Выч[ (z), zk ]= ?
3.
1) znнуль порядка n
f z z zn f1 z , f1 zn 0.
n
'
n
f1 z
z
z zn f1 z
Выч z , zn n
4.
2) z pf z
полюс порядка p
f2 z
z z p
, f 2 z p 0.
p
'
p
f2 z
z
z z p f2 z
Выч z , z p p
5.
Теорема 19.1 Если f z Cz p - полюса,
g \ z1 , , z M
f g 0 , то
1
f '( )
d N P ,
2 i f ( )
g
где N- полное число нулей f(z) с учетом
кратности, P- полное число полюсов
f(z) с учетом кратности.
6.
Доказательство. По основной теореметеории вычетов
M
( )d 2 i Выч ( z ), zk
g
k 1
P
N
2 i nk n p 2 i N P
k 1
k 1
7.
В частности, если f z C1
f '( )
N
d
2 i f ( )
g
g
8. Принцип аргумента.
1f '( )
1
d
d ln f ( )d
2 i f ( )
2 i
g
g
1
1
d ln f ( )
d arg f ( )
2 i
2
g
g
1
1
Var ln f ( ) g Var arg f ( ) g
2 i
2
9.
ln f ( ) действительная, однозначнаяVar ln f ( ) g 0.
1
N P Var arg f ( ) g
2
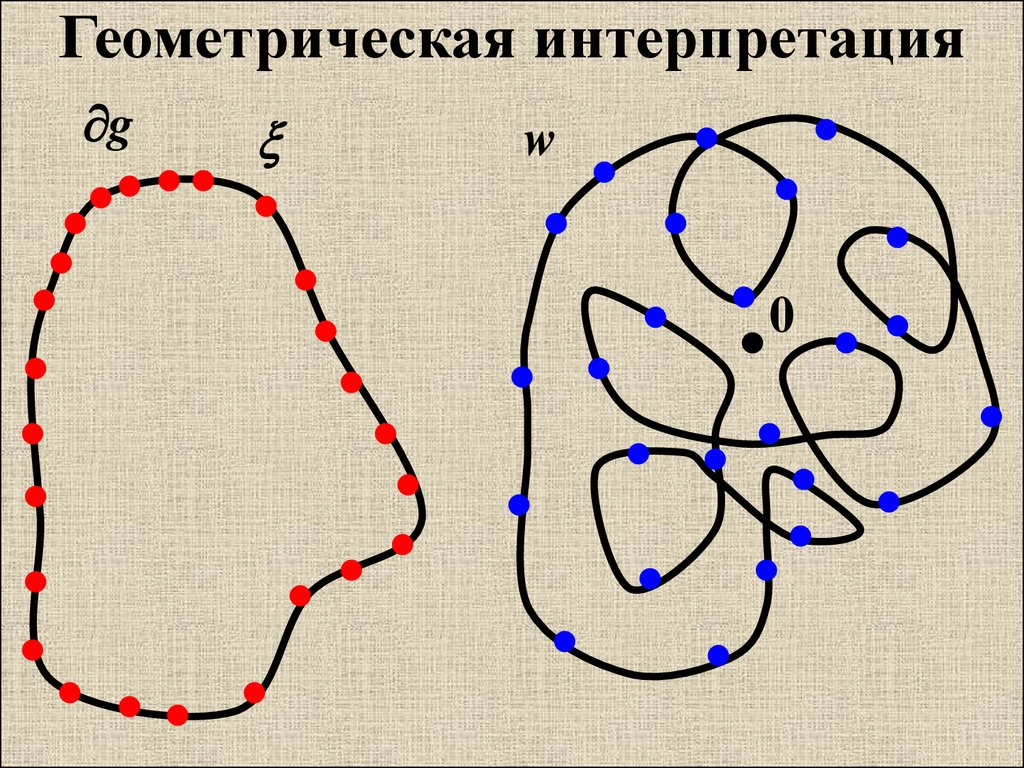
10. Геометрическая интерпретация
gw
0
11.
Принцип аргумента. Разность междуполным числом нулей и полюсов
функции f(z) в области g определяется
числом оборотов, которое совершает
точка w=f(z) вокруг точки w=0, при
положительном обходе точкой z
контура g.
12. Теорема Руше
Если f z , z C gf z g z g , то N f N f
g
g
13.
f z CДоказательство.
g
f z g не имеет особых точек.
f z g z g f z g 0.
F z f z z C
g
F z g не имеет особых точек.
14.
F z g f z z g f z g z g 0f z , F z f z z Т .19.1
1
N f g Var arg( f ) g
2
1
N f g Var arg( f ) g
2
N f g N f g
1
Var arg( f ) arg f g *
2
15.
z1 z1 ez1
z2
i arg( z1 )
, z2 z2 e
i arg( z2 )
z1 i arg( z1 ) arg( z2 )
e
z2
z1
arg( z1 ) arg z2 arg
z2
16.
f1
* Var arg
2
f g
1
Var arg 1
2
f g
w 1
f
w 1
f
w 1
f
1
17.
gw
0
1
1
Var arg 1 0
2
f g
18. Основная теорема высшей алгебры.
Полином n-ой степени имеет накомплексной плоскости ровно n нулей
(с учетом их кратности).
19.
Доказательство.F z an z an 1z
n
n 1
a1z a0
f z z
f z an z
n
z an 1z
n 1
z an 1 n 1
a1
a0
z
z
f z
an
an
an
a1z a0
20.
an , an 1 , , a1 , a0 R0 : z R R0f z
0
1 т . Руше
z z R
N F z R N f z R
f z an z
n
z 0 корень кр. n
N F z R N f z R n


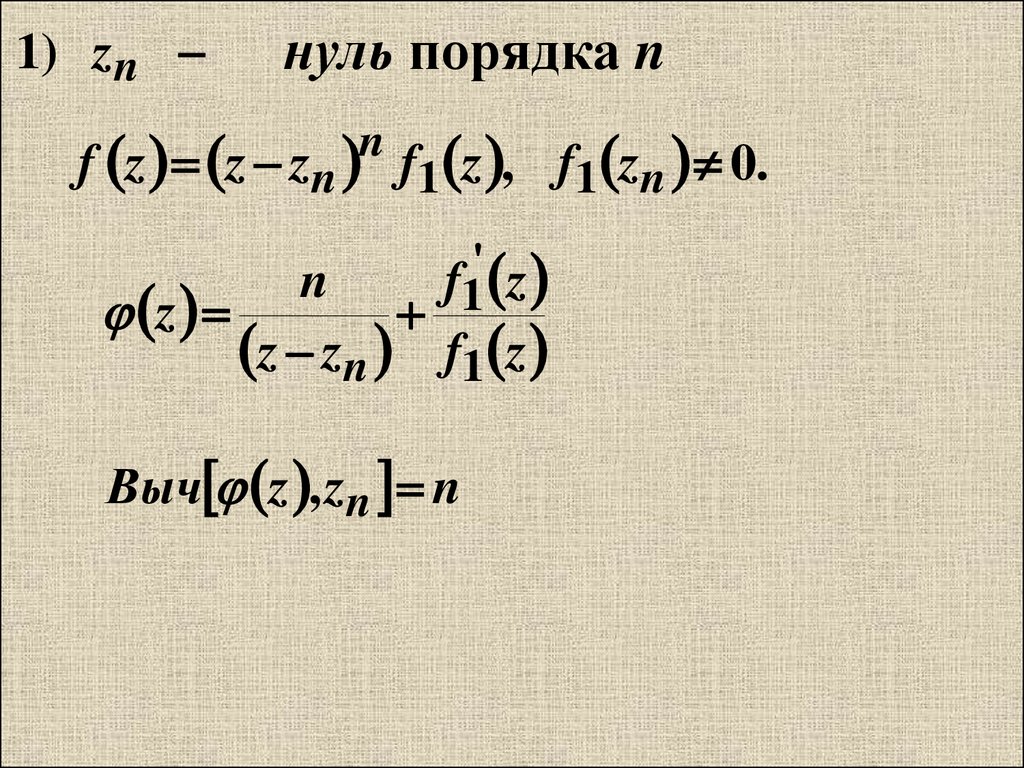
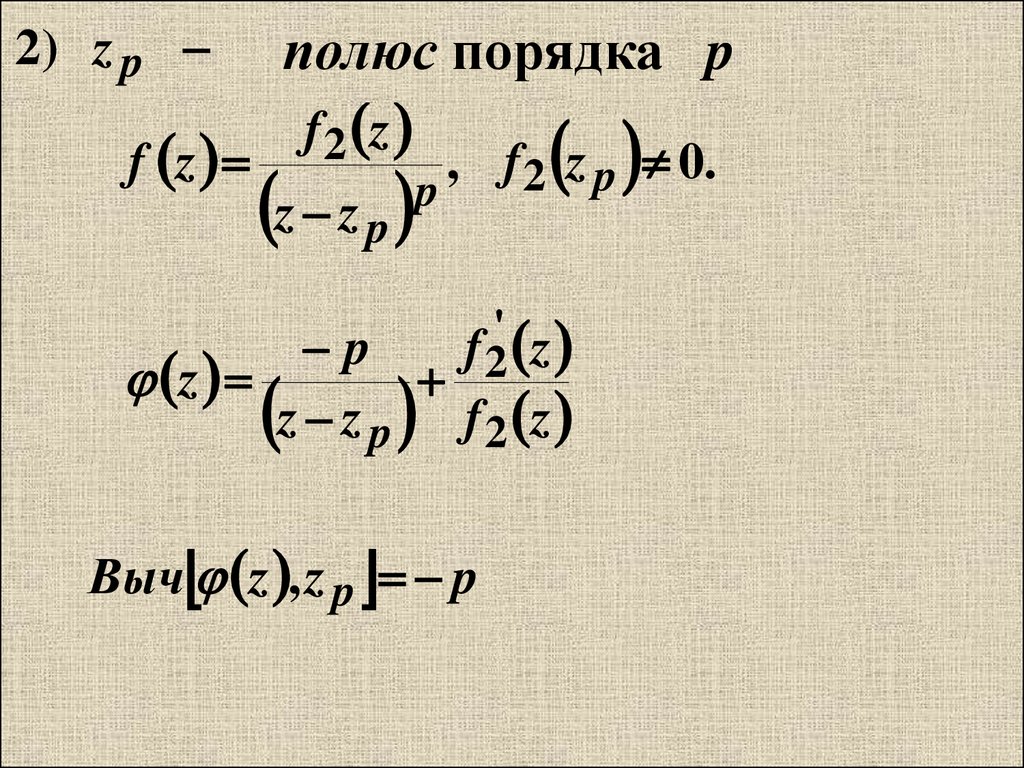


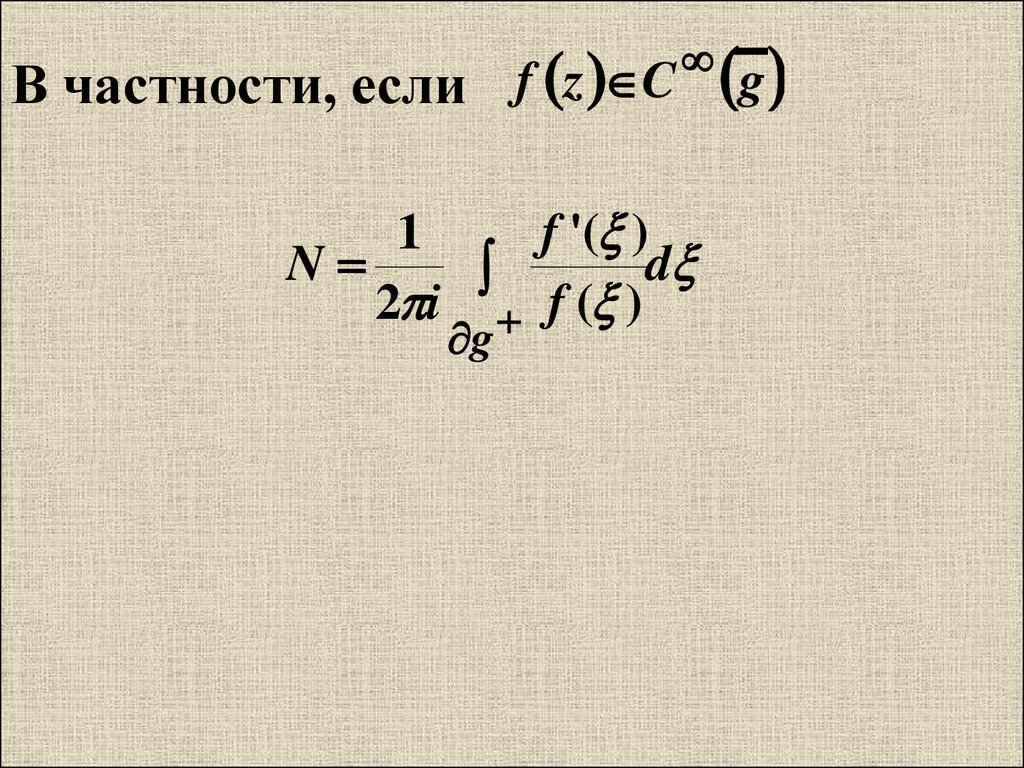






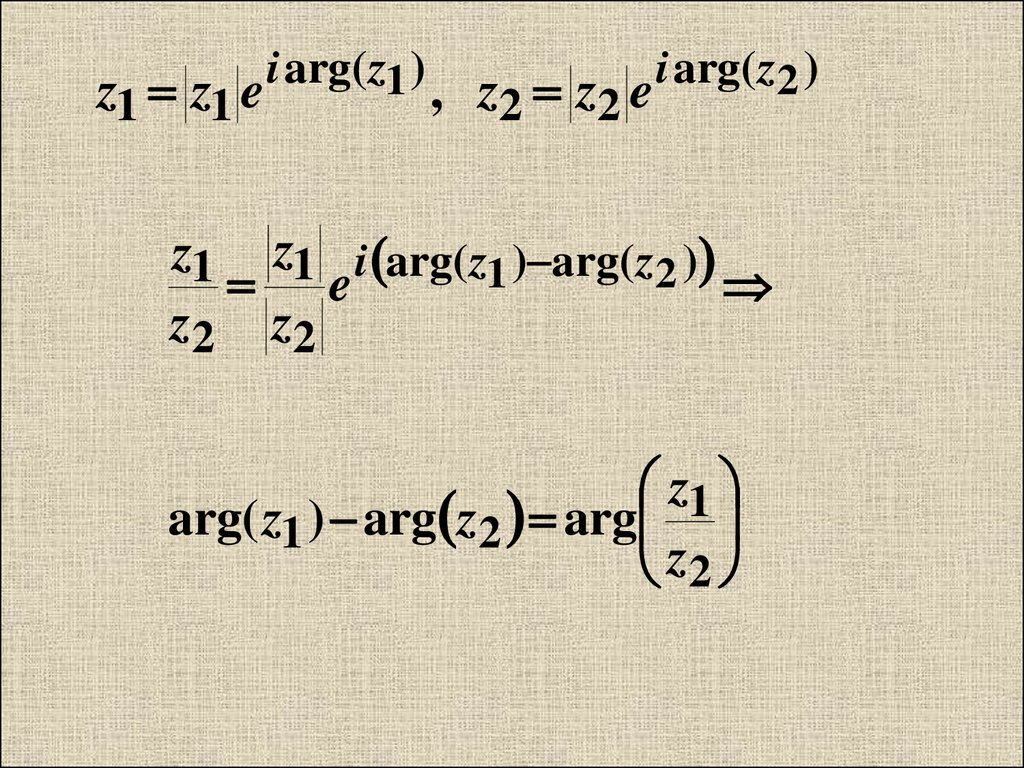




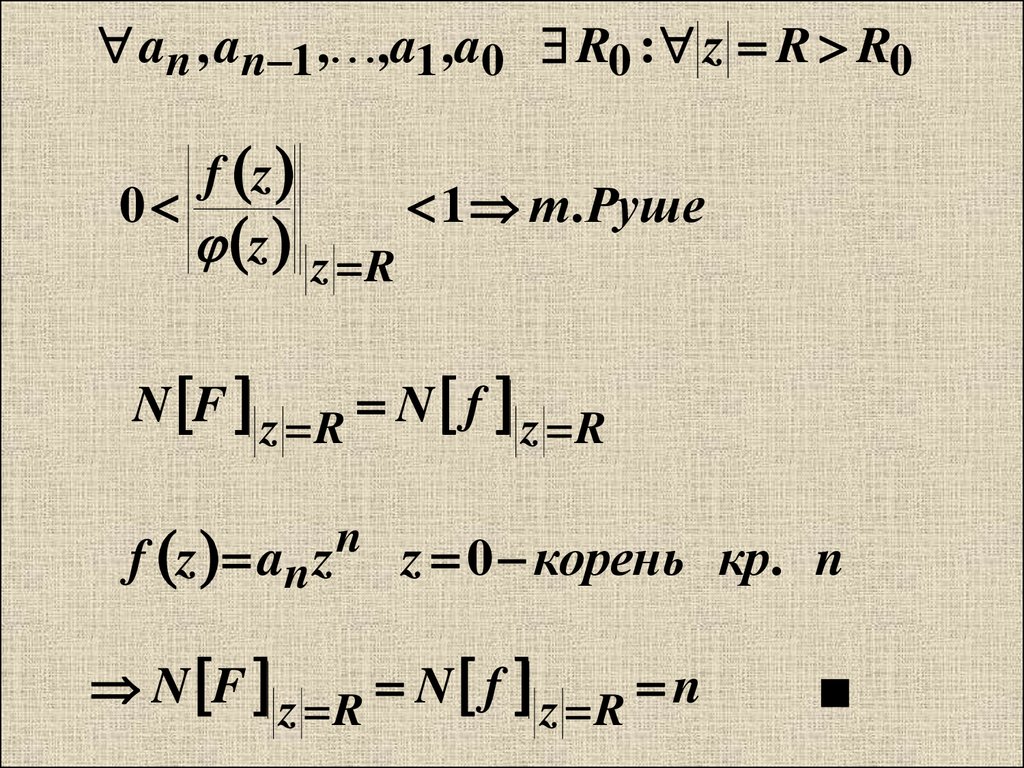
 mathematics
mathematics








