Similar presentations:
Действительные числа. Материалы по математике для обучающихся 10 класса
1. Действительные числа.
Материалы по математике дляобучающихся 10 класса.
2. Содержание темы:
1.2.
3.
4.
5.
6.
Действительные числа.
Бесконечно убывающая геометрическая прогрессия.
*Арифметический корень натуральной степени.
*Тождественные преобразования выражений с
арифметическим корнем натуральной степени.
*Степень с рациональным показателем.
*Степень с действительным показателем.
3. Результатом изучения темы является:
умение на базовом уровне:находить значения корня натуральной степени,
степени с рациональным показателем;
проводить по известным формулам и правилам
преобразования буквенных выражений,
включающих степени, радикалы;
вычислять значения числовых и буквенных
выражений, осуществляя необходимые
подстановки и преобразования;
решать простейшие иррациональные уравнения,
их системы.
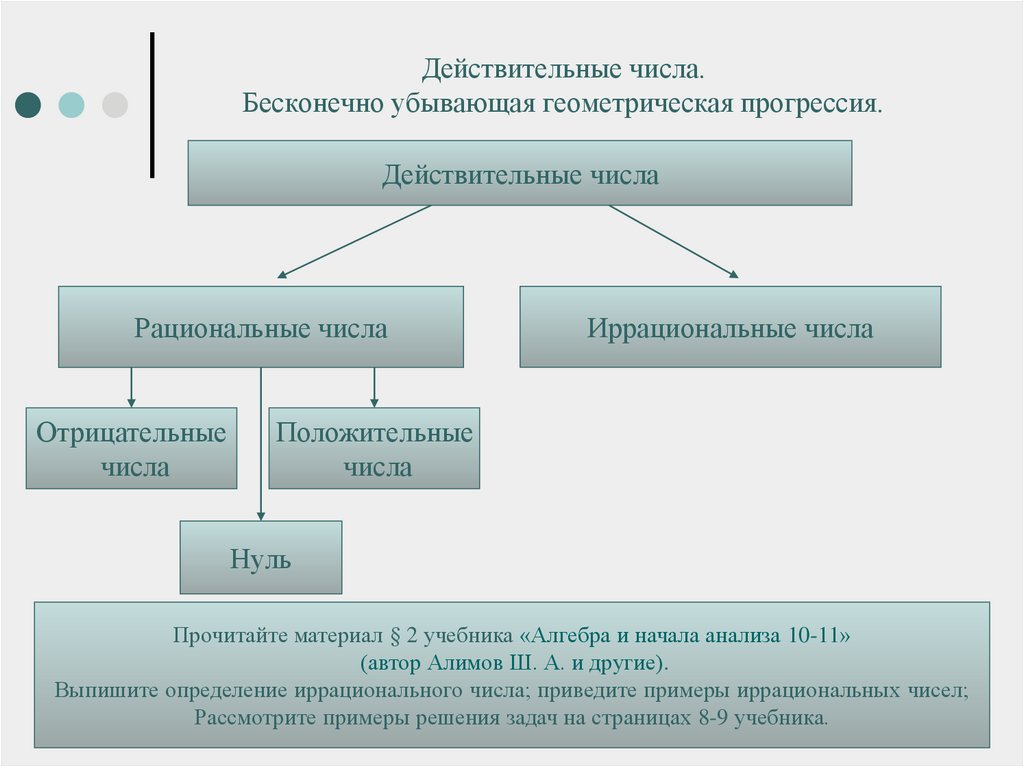
4. Действительные числа. Бесконечно убывающая геометрическая прогрессия.
Действительные числаРациональные числа
Отрицательные
числа
Иррациональные числа
Положительные
числа
Нуль
Прочитайте материал § 2 учебника «Алгебра и начала анализа 10-11»
(автор Алимов Ш. А. и другие).
Выпишите определение иррационального числа; приведите примеры иррациональных чисел;
Рассмотрите примеры решения задач на страницах 8-9 учебника.
5. Действительным числом называется бесконечная десятичная дробь вида , где - целое число, а каждая из букв , , - это одна из
Действительным числом называется бесконечнаядесятичная дробь вида 0 , 1 2 3 , где а0
- целое число, а каждая из букв 1 , а 2 , а3 - это
одна из десяти цифр: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9.
а аа а
а
Примеры:
1. Выясните, каким числом (рациональным или иррациональным)
является числовое значение выражения:
( 8 3)(3 2 2 ) ( 4 2 3)(3 2 2 )
( 4
2 3)(3 2 2 ) ( 2 2 3)(3 2 2 )
8 9 1
Число -1 является рациональным (его можно представить в виде дроби).
63
28
9 7
4 7
2. Вычислить:
9
7
4
7 3 2
49
6 7 42
Выполните самостоятельно: из § 2 учебника «Алгебра и начала анализа 1011» (автор Алимов Ш. А. и другие) упражнение № 9 (2-4), упражнение
№ 10 (2-4).
6. Бесконечно убывающая геометрическая прогрессия.
Определение:Числовая последовательность, первый член которой
отличен от нуля, а каждый последующий член,
начиная со второго, равен предшествующему члену,
умноженному на одно и то же не равное нулю число,
называется геометрической прогрессией.
1 1 1 1 1
Пример:
1, , , , , ,
2 4 8 16 32
Знаменатель геометрической прогрессии g =
а а а
а а а
2
3
4
1
2
3
Геометрическая прогрессия называется убывающей, если
модуль её знаменателя меньше единицы.
7.
Пример.Выяснить, является ли геометрическая прогрессия бесконечно
3
убывающей:
12, b11
b
7
Решение:
3 4
b 12, b 4
b b g b b g
b b g g
b
b g
7
11
6
7
1
11
10
1
10
4
1
11
6
7
g
1
4
3
4
12
4
1
1
16
2
Так как знаменатель геометрической прогрессии меньше 1, то это
убывающая геометрическая прогрессия.
Выполните самостоятельно: упражнение № 16 (3).
8. Арифметический корень натуральной степени.
Определение:Арифметическим корнем натуральной степени п ≥ 2 из неотрицательного
числа а называется неотрицательное число b, п-я степень которого равна
а.
n
n
a b, b a; a 0, b 0
Рассмотрите свойства арифметического корня натуральной степени на
странице 19 учебника.
3
6
729
729 3
Примеры:
1 4
1
4
81 625 3 5 1 5 4
3
3
3
343 0,125 343 0,125 7 0,5 3,5
3
3
6
( х)
3
3
х
6
3 ( х )3 х
2
2
548 2 420 2 (548 420) (548 420)
128 968 64 2 484 2 64 484 4
5
19 5 243 5 243 3
7
5
1,5
32
32
32 2
8 22 2 174
9. Тождественные преобразования выражений с арифметическим корнем натуральной степени: примеры заданий из Открытого Банка Задач
Единого Государственного Экзаменапо математике.
9
7 18 7 18 7 2 18 7 18 7 3
1
6
18 3
18 3
7
7
7
5482 420 2 (548 420) (548 420) 128 968 64 2 484 2 64 484 4
8 22 2 352
5 3 9 6 9 5 6 9 2 6 9 5 6 93 5 6 (32 ) 3 5 6 36 5 3 15
(а 6) 2 (а 10) 2 , если 6 а 10.
(а 6) 2 а 6 а 6; (а 10) 2 а 10 10 а, то
(а 6) 2 (а 10) 2 (а 6) (10 а ) а 6 10 а 4
10. Степень с рациональным показателем.
Если п – натуральное число, m – целое число, то при а >0m
справедливо равенство:
m
п
а
an
Примеры:
4
1
2
3
4
b b ;
3
5
1 5 1
x
x
2
3
x
1
5
64 64 8; 8 8 (2 ) (2 ) 2 4
3
2
3
3 2
3
2 3
2
11. Свойства степени с рациональным показателем.
аm
a
n
a
m n
m
a
m n
a
n
a
m
n
m n
(a ) a
( ab)
n
a
n
n
a n
a
(
)
n
b
b
b
n
12. Примеры решения заданий из Открытого Банка Задач Единого Государственного Экзамена по математике
6n1
3
1
12
n n
1
4
6 п
1 1 1
3 12 4
4 1 3
12 12 12
6 п
6 п 0 6 1 6
a 3,33
2
при
а
a 2,11 a 2, 22
7
.
a 3,33
а 3,33
2 1 7
3, 33 4 , 33
1
а
а
(
) 3,5
2 ,11 2 , 22
4 , 33
а
а
7
2
n
1
12
5
6
1
4
n n
п 64
п
5 1 1
6 12 4
10 1 3
12 12 12
п
6
12
1
2
п п п 64 8
13. Задания для домашней работы.
1. Выполните упражнение № 60на странице 31 учебника.
2. Вычислите значения
выражений № 70.
3. Прочитайте решение задачи
№ 4 на странице 15 учебника.
4. Выполните упражнение № 20
Вычислите:
2 x x : 3x
3 4
2 6
2
49 43 : 196
6,5
3
9
2 , 25
3
5 10
5 5
3
12












 mathematics
mathematics








