Similar presentations:
Степень с натуральным показателем
1.
N –натуральные числаZ – целые числа
Q - рациональные числа
2. Найдите значения выражений:
3+3+3+3=2+2+2+2+2+2+2=
Упростите выражение:
х+х+х+…+х+х=
п слагаемых
3.
Найдите площадьквадрата со
стороной 10 см.
Найдите объем куба с
ребром 0,5 см.
S = а2
S = 102 = 100(см2)
V = а3
V = 0,53= 0,125 (см3)
4.
1)10 · 10 = 1022) 28 · 28 · 28 = 283
3) 3· 3 · 3 · 3 · 3 · 3 · 3 · 3 · 3 = 39
4) 1,5· 1,5· 1,5· 1,5· 1,5· 1,5 = 1,56
5) (-2с)· (-2с)· (-2с)· (-2с)· (-2с) =(-2с)5
6) (х+y) · (х+y) · (х+y) · (х+y) =(х+y)4
5.
Степень снатуральным
показателем
6. 56; 3,75; 04; (-4,8)6
Степень с натуральным показателемпоказатель степени
ап =а•а•а•…•а•а
n множителей
основание степени
56; 3,75; 04; (-4,8)6
7.
Степенью числа а с натуральнымпоказателем n(п≥ 2)называется
произведение n множителей, каждый из
которых равен а.
Степенью числа а с показателем 1
называется само число а. (а1=а)
Операцию отыскания степени называют
возведением в степень.
8.
№1. Представьте в виде произведениятретью степень числа 4 и найдите
ее числовое значение.
43 = 4·4·4 =64
№2. Чему равна сумма кубов чисел 5 и 3 ?
53 + 33 = 125 + 27 =152
9.
№3. Вычислите:= 125
1) 5 3
2) 24 – 62 = -20
3) (-4) 2+ 25 = 48
4) 1 7 – 92 + 10 3 = 920
№4. Представьте данное число в виде
степени какого-либо числа с показателем,
отличным от 1.
1) 64 =43
2)36 =62
3)121 =112 4)27 =33
10.
№ 5. Найдите х, если1)2х = 32; 2) х 3 = 125
2 х= 25
х 3= 53
х=5
х=5
№ 6. Вычислите квадрат
куба числа:
1)2
(23) 2 =64
2)4
(43)2=4096
11.
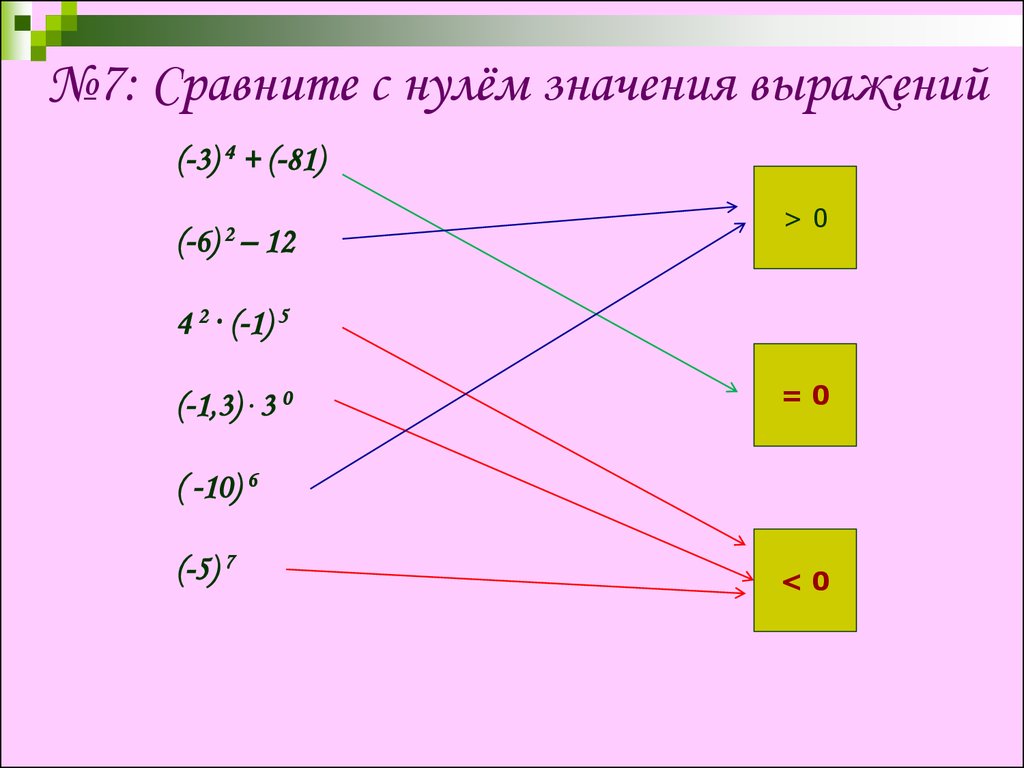
№7: Сравните с нулём значения выражений(-3) 4 + (-81)
(-6)
2–
12
>0
4 2 · (-1) 5
(-1,3) · 3 0
=0
( -10) 6
(-5) 7
<0
12.
Какую закономерностьможно заметить?
(-2)1 =(- 2) = -2
(-2)2 = (- 2) (- 2) = 4
(-2)3 = (- 2) (- 2) (- 2) = -8
(-2)4 = (- 2) (- 2) (- 2) (- 2) = 16
(-2)5 = (- 2) (- 2) (- 2) (- 2) (- 2) = -32
(-2)6 = (- 2) (- 2) (- 2) (- 2) (- 2) (- 2) = 64
(-2)7 = (- 2) (- 2) (- 2) (- 2) (- 2) (- 2) (- 2) = -128
(-2)8 = (- 2) (- 2) (- 2) (- 2) (- 2) (- 2) (- 2) (- 2) = 256
(-2)9 = (- 2) (- 2) (- 2) (- 2) (- 2) (- 2) (- 2) (- 2) (- 2) = -512
(-2)10 = (- 2) (- 2) (- 2) (- 2) (- 2) (- 2) (- 2) (- 2) (- 2) (- 2) = 1024
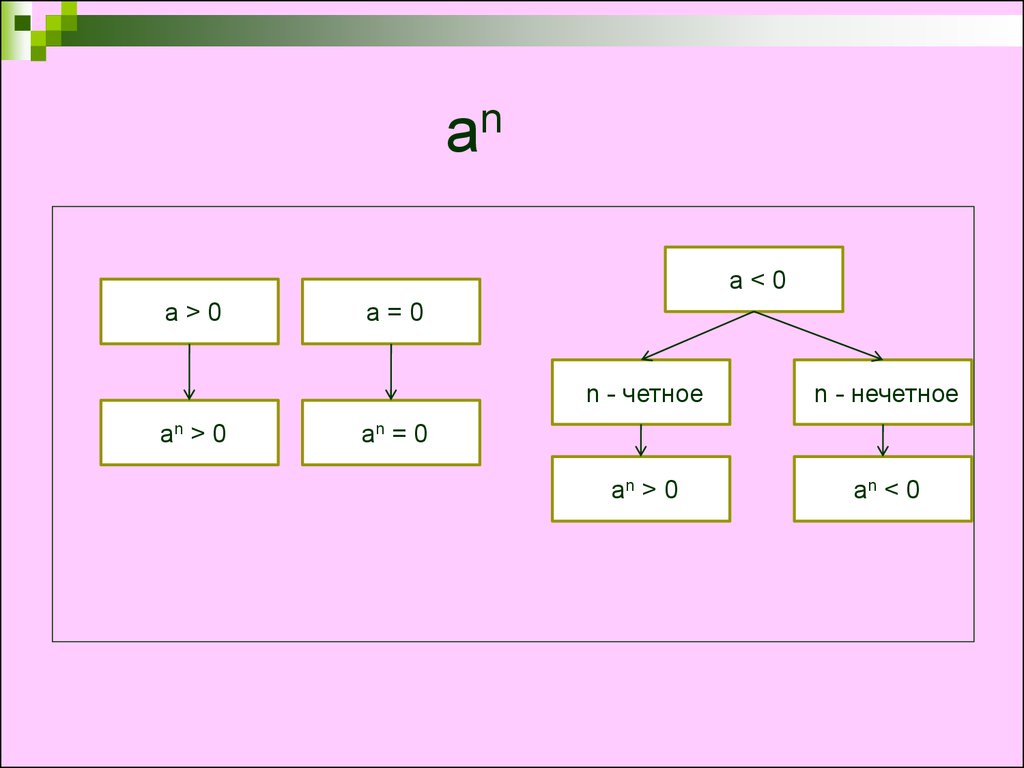
13. an
a<0a>0
an > 0
a=0
n - четное
n - нечетное
an > 0
an < 0
an = 0
14.
5) -24 и (-2)415.
1) а4; 34 = 812) 0,251 = 0,25
3) 0100 = 0
4) 125 = 53
5) -24 < (-2)4
16.
Из истории степенейУ древних вавилонян, египтян и
китайцев имелись некоторые отдельные
знаки – иероглифы для немногих
математических понятий. Однако лишь
в «Арифметике »
Диофанта (3в)
встречаются зачатки алгебраической
буквенной символики.
17.
Сложение, вычитание,умножение и деление идут
первыми в списке
арифметических действий. У
математиков не сразу сложилось
представление о возведении в
степень как о самостоятельной
операции, хотя в самых древних
математических текстах Древнего
Египта и Междуречья
встречаются задачи на
вычисление степеней.
18.
Европейские математики 16 века вторую степеньнеизвестного называли «сила», а также «квадрат», третью
степень – «куб».
Немецкие математики Средневековья стремились
ввести единое обозначение и сократить число символов.
Книга Михаэля Штифеля «Полная арифметика» (1544 г.)
сыграла в этом значительную роль.
19. Вильям Оутред (1575-1660)– английский математик
Вильям Оутред (15751660)– английскийматематик
Aq вместо A2
Ac вместо A3
Aqqвместо A4
20. Франсуа Виет (1540-1603) – французский матемматик
Франсуа Виет (15401603) – французскийматемматик
Виет применял
сокращения:
N для первой степени,
Q для второй степени,
C для третьей степени,
QQ для четвертой и т. д.
Например
1C-8Q+16N aequatur 40
означает :
x3 – 8x2 + 16x = 40
21. Михаэль Штифель (1487г.-19.04.1567г.) -немецкий математик
Михаэль Штифель(1487г.-19.04.1567г.) немецкий математик
ААА вместо А3
22. Томас Гарриот (1560-1621)-английский математик
Томас Гарриот (1560-1621)английский математикаааа вместо а4
23. Рене Декарт (1596-1650) –французский математик
Рене Декарт (15961650) –французскийматематик
Рене Декарт в его
«Геометрии» (1637)
впервые ввёл
современное
обозначение степеней
24.
В физике:10 = 101
100 = 102 (санти)
1000 = 103 (кило)
1000000 = 106 (Мега)
1000000000 = 109 (Гига)
При переводе
единиц измерения:
72 км = 72000 м = 72∙103 м
5кг = 5000 г = 5∙103г
25.
26.
В астрономии расстояния до звезд измеряют вастрономических единицах (а.е.).
1 а.е. = 1,496∙108 км
1 световой год = 9,46 ∙ 108 км
Самая близкая к нам звезда (из созвездия
Центавра) находится на расстоянии:
206265 а.е. =3,08∙1013 км = 3,26 св. лет
27. Миаил Васильевич Ломоносов (1711-1765)-русский учёный
Миаил ВасильевичЛомоносов (1711-1765)русский учёный
“Пусть кто-нибудь попробует
вычеркнуть из математики
степени, и он увидит, что без
них далеко не уедешь”
М.В.Ломоносов
28.
Найти значение выраженияn2 + k2 , если 2n = 32 и 3k = 9.

























 mathematics
mathematics








