Преобразование графиков функций

1.

Преобразования
графиков функций

2.

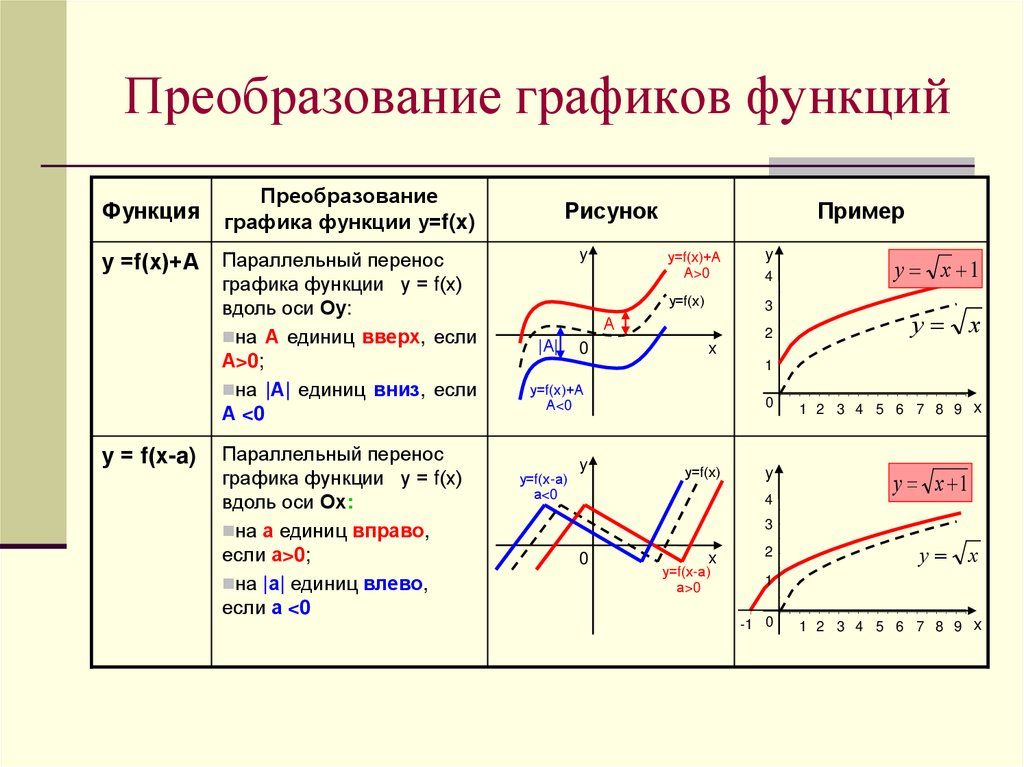
Преобразование графиков функций
Функция
Преобразование
графика функции у=f(x)
Рисунок
у
у =f(х)+А Параллельный перенос
графика функции у = f(х)
вдоль оси Оу:
на А единиц вверх, если
А>0;
на |А| единиц вниз, если
А <0
у = f(х-a)
Параллельный перенос
графика функции у = f(х)
вдоль оси Ох:
на а единиц вправо,
если а>0;
на |а| единиц влево,
если а <0
Пример
у=f(х)+А
А>0
у=f(х)
0
4
3
А
|А|
у
х
2
у х 1
у х
1
у=f(х)+А
А<0
у=f(х-а)
а<0
у
0
у=f(х)
у
4
1 2 3 4 5 6 7 8 9
х
у х 1
3
0
х
у=f(х-а)
а>0
2
у х
1
-1 0
1 2 3 4 5 6 7 8 9
х

3.

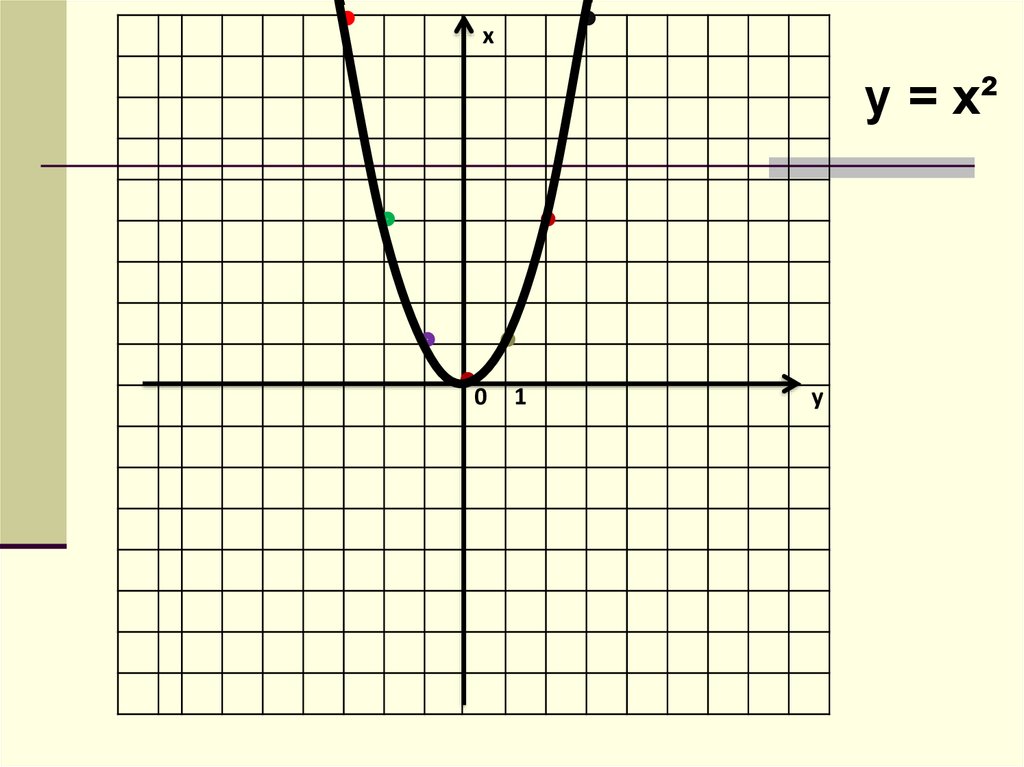
х
у = х²
0
1
у

4.

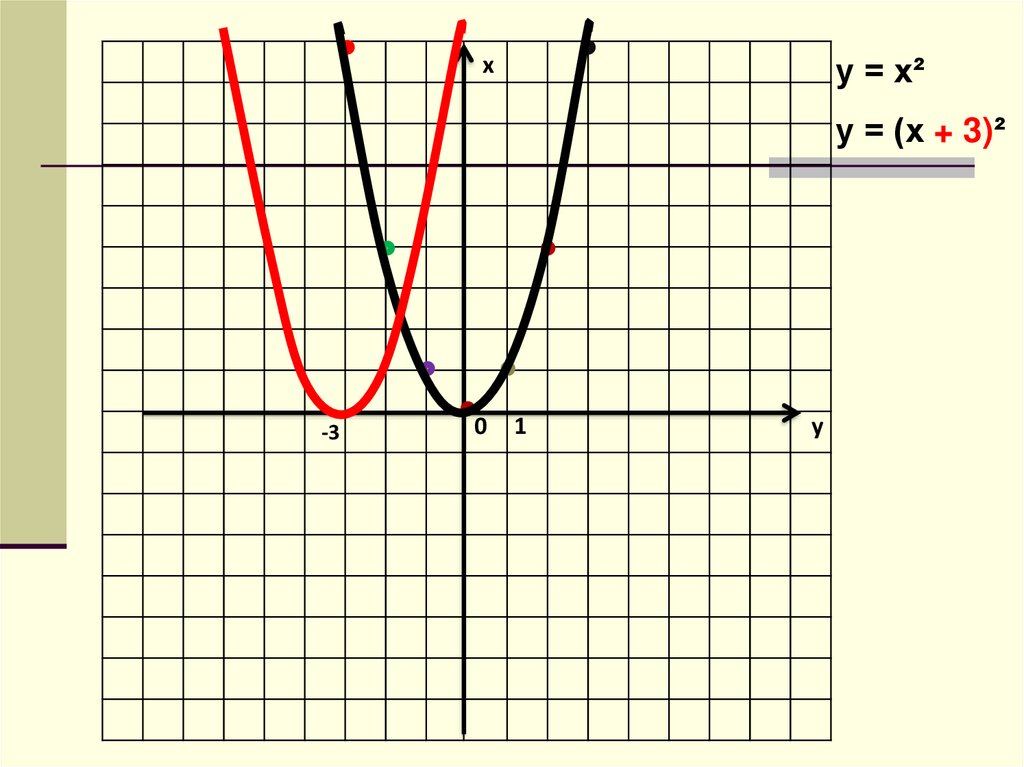
у = х²
х
у = (х + 3)²
-3
0
1
у

5.

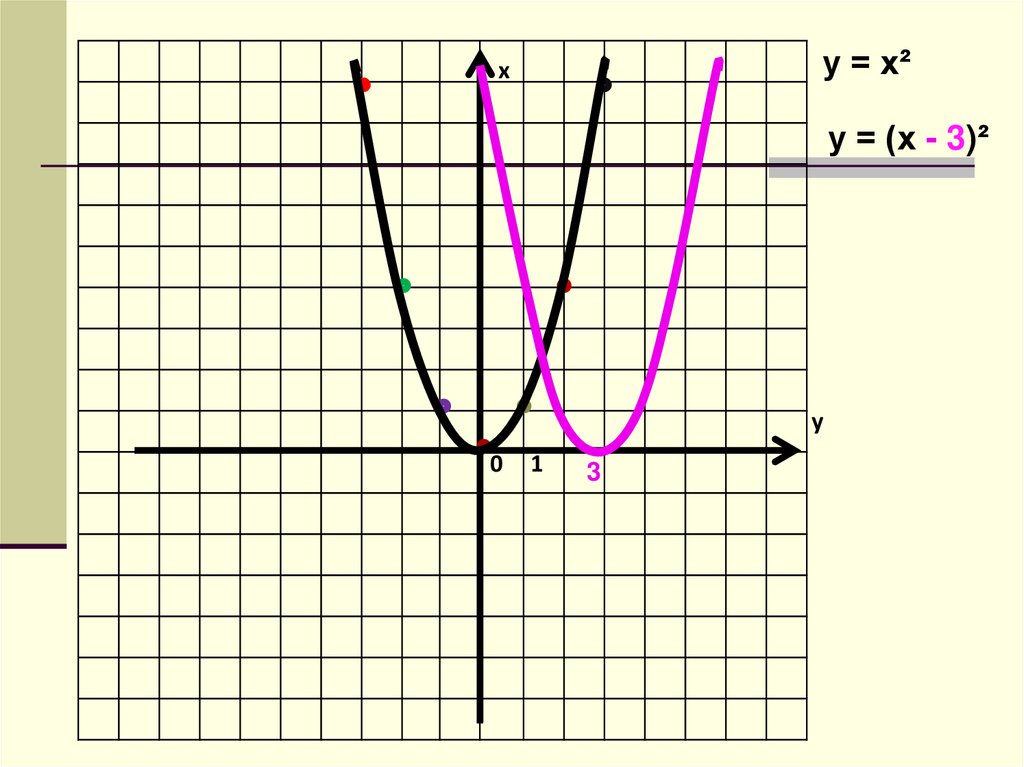
у = х²
х
у = (х - 3)²
у
0
1
3

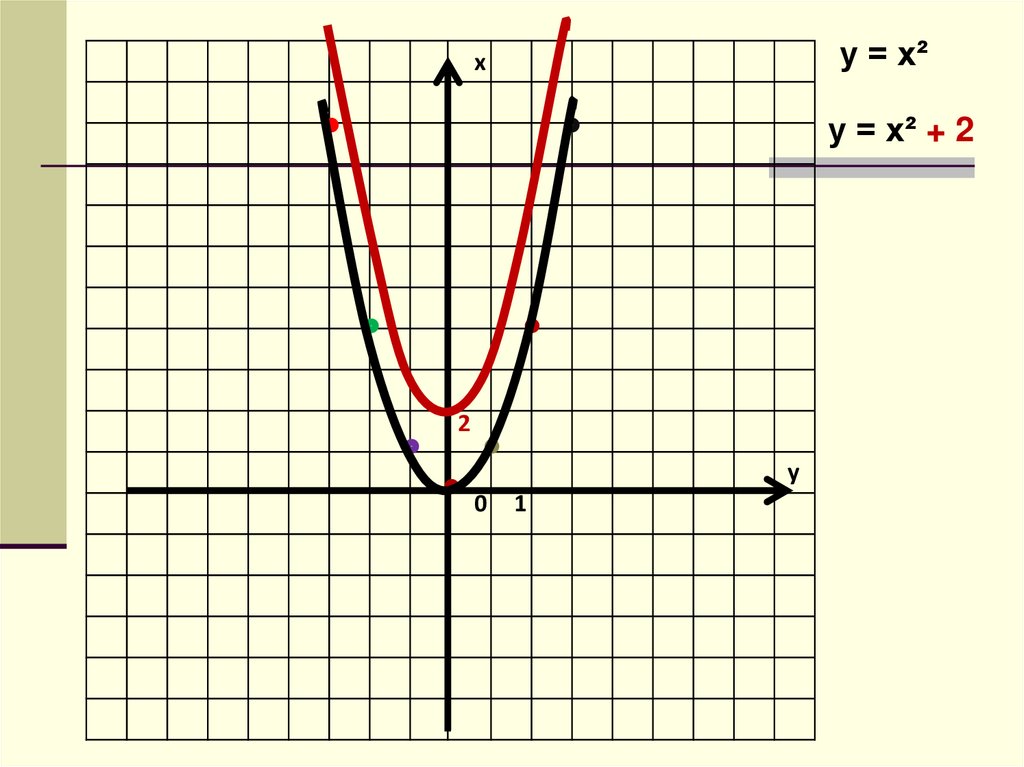
6.

у = х²
х
у = х² + 2
2
у
0
1

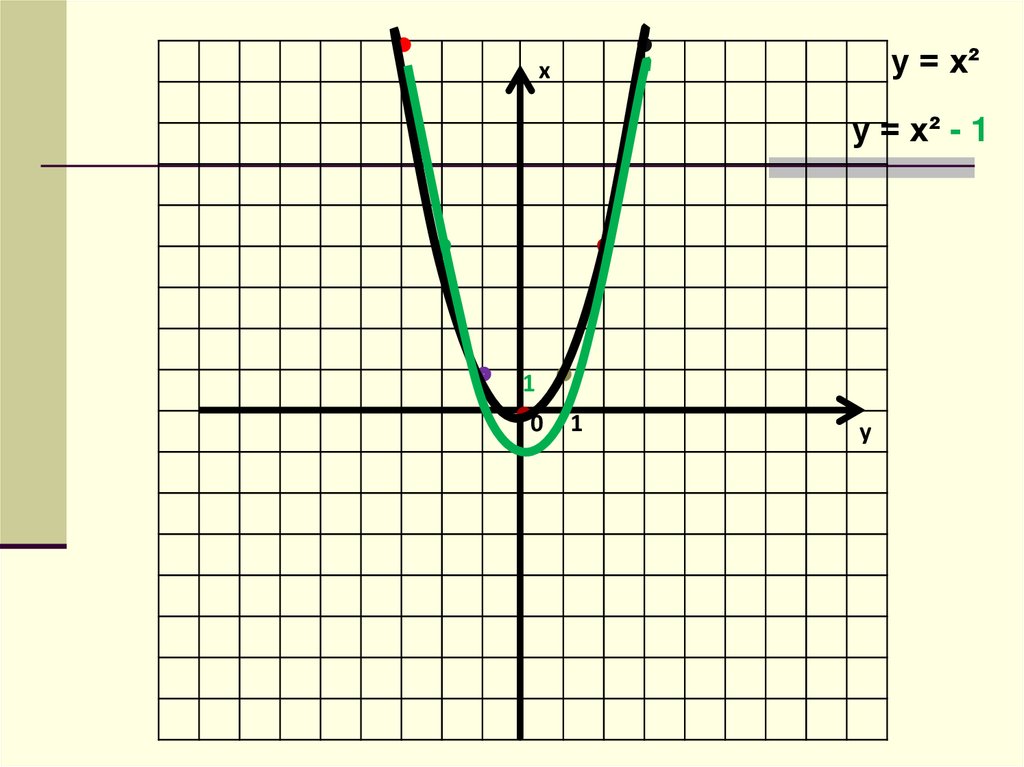
7.

у = х²
х
у = х² - 1
1
0
1
у

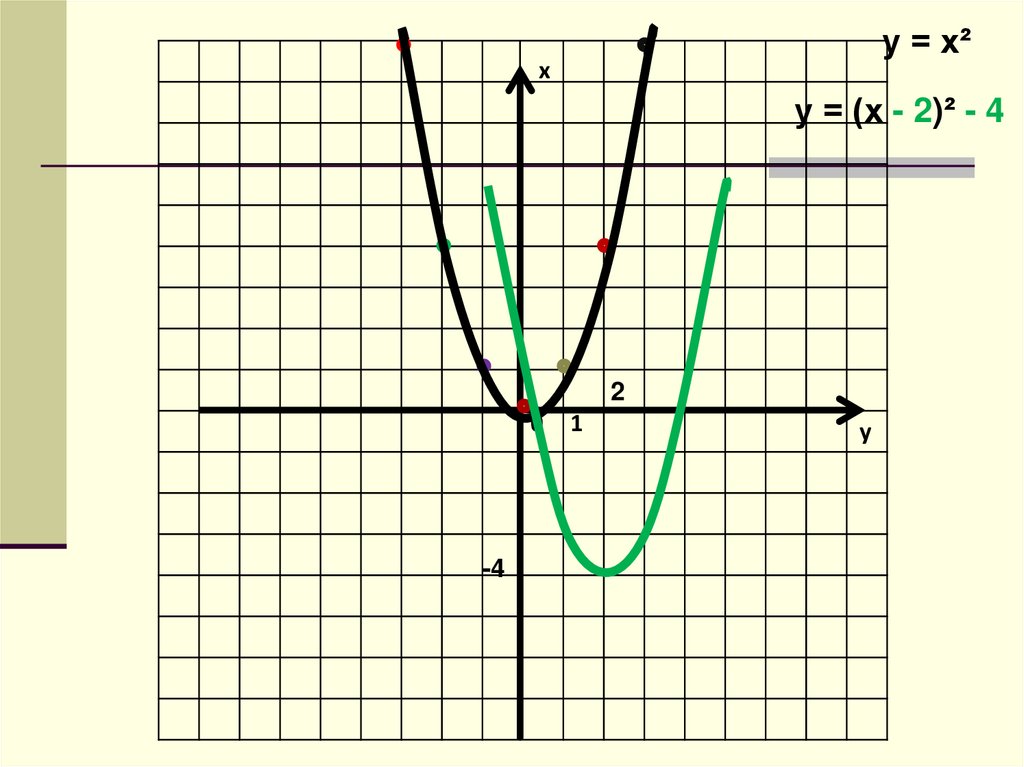
8.

у = х²
х
у = (х - 2)² - 4
2
0
-4
1
у

9.

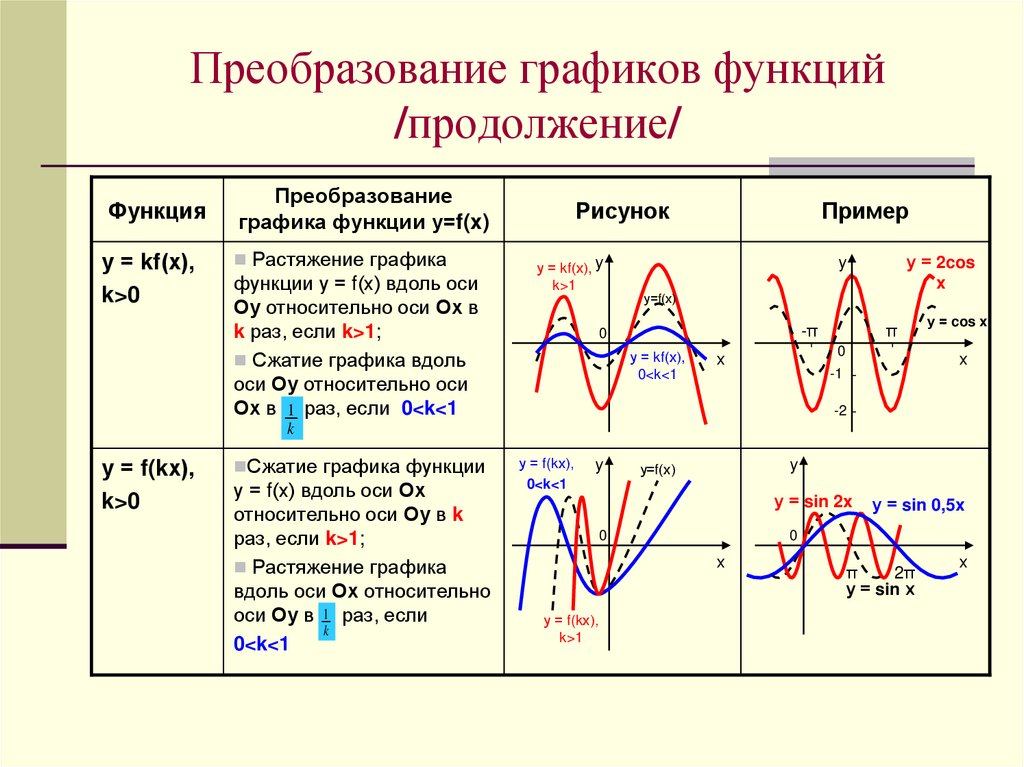
Преобразование графиков функций
/продолжение/
Функция
у = kf(х),
k>0
Преобразование
графика функции у=f(x)
Растяжение графика
функции у = f(х) вдоль оси
Оу относительно оси Ох в
k раз, если k>1;
Сжатие графика вдоль
оси Оу относительно оси
Ох в 1 раз, если 0<k<1
Рисунок
у = kf(х), у
k>1
Пример
у
у = 2cos
x
у=f(х)
π
-π
0
у = kf(х),
0<k<1
0
х
у = cos x
х
-1
-2
k
у = f(kх),
k>0
Сжатие графика функции
у = f(х) вдоль оси Ох
относительно оси Оу в k
раз, если k>1;
Растяжение графика
вдоль оси Ох относительно
оси Оу в 1 раз, если
k
0<k<1
у = f(kх),
0<k<1
у
у
у=f(х)
у = sin 2x
0
0
х
у = f(kх),
k>1
у = sin 0,5x
π
2π
у = sin х
х

10.

Преобразование графиков функций
/продолжение/
Функция
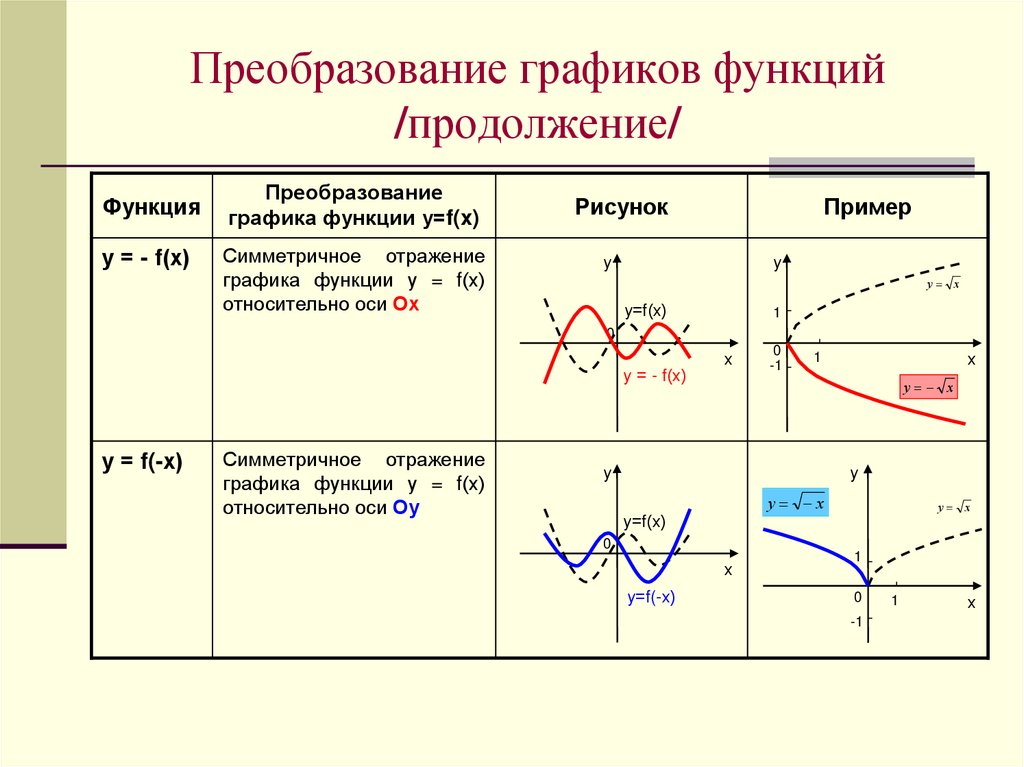
у = - f(х)
Преобразование
графика функции у=f(x)
Симметричное отражение
графика функции у = f(х)
относительно оси Ох
Рисунок
Пример
у
у
у х
у=f(х)
1
0
у = - f(х)
у = f(-х)
Симметричное отражение
графика функции у = f(х)
относительно оси Оу
х
0
-1
х
1
у х
у
у
у х
у=f(х)
0
х
у=f(-х)
у х
1
0
-1
1
х

11.

Преобразование графиков функций
/продолжение/
Функция
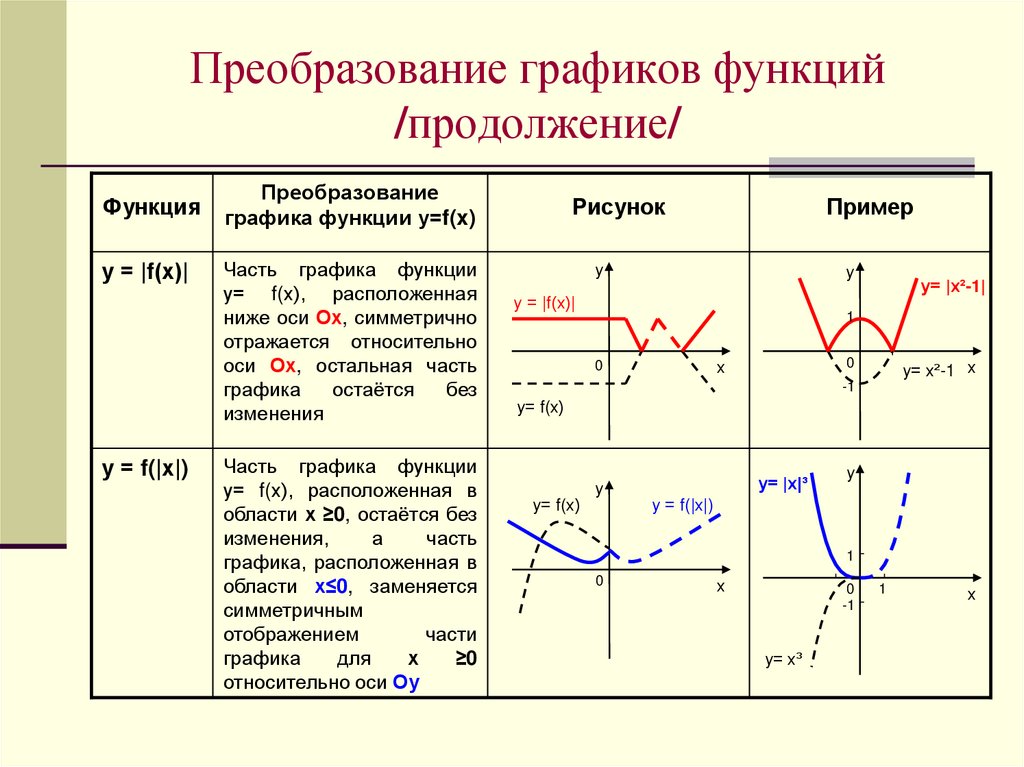
у = |f(х)|
у = f(|х|)
Преобразование
графика функции у=f(x)
Часть графика функции
у= f(х), расположенная
ниже оси Ох, симметрично
отражается относительно
оси Ох, остальная часть
графика
остаётся
без
изменения
Часть графика функции
у= f(х), расположенная в
области х ≥0, остаётся без
изменения,
а
часть
графика, расположенная в
области х≤0, заменяется
симметричным
отображением
части
графика
для
х
≥0
относительно оси Оу
Рисунок
Пример
у
у
у = |f(х)|
у= |х²-1|
1
0
х
0
у= х²-1 х
-1
у= f(х)
у= f(х)
у
у= |х|³
у
у = f(|х|)
1
0
х
0
-1
у= х³
1
х