Магнитное поле. Лекция 27

1. Магнитное поле - 2

ВоГУ
Лекция 27 (9)
Магнитное поле - 2
Кузина Л.А.,
к.ф.-м.н., доцент
2017 г.
1

2. План

2

3.

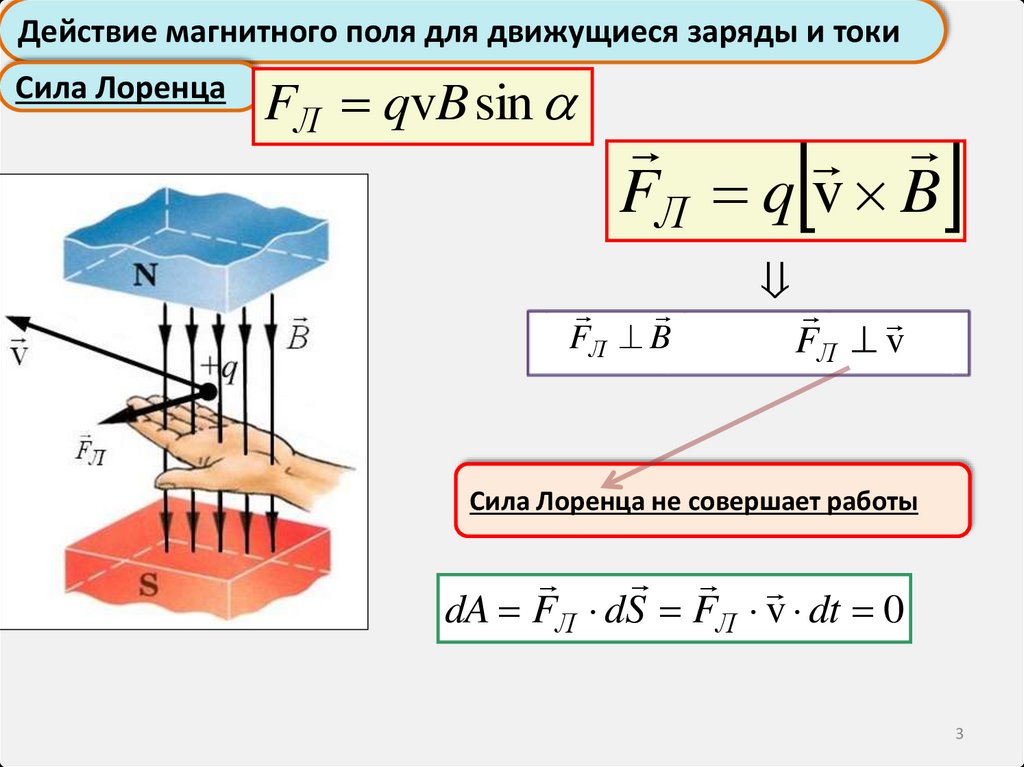
Действие магнитного поля для движущиеся заряды и токи
Сила Лоренца
FЛ qvB sin
FЛ q v B
FЛ B
FЛ v
Сила Лоренца не совершает работы
dA FЛ dS FЛ v dt 0
3

4.

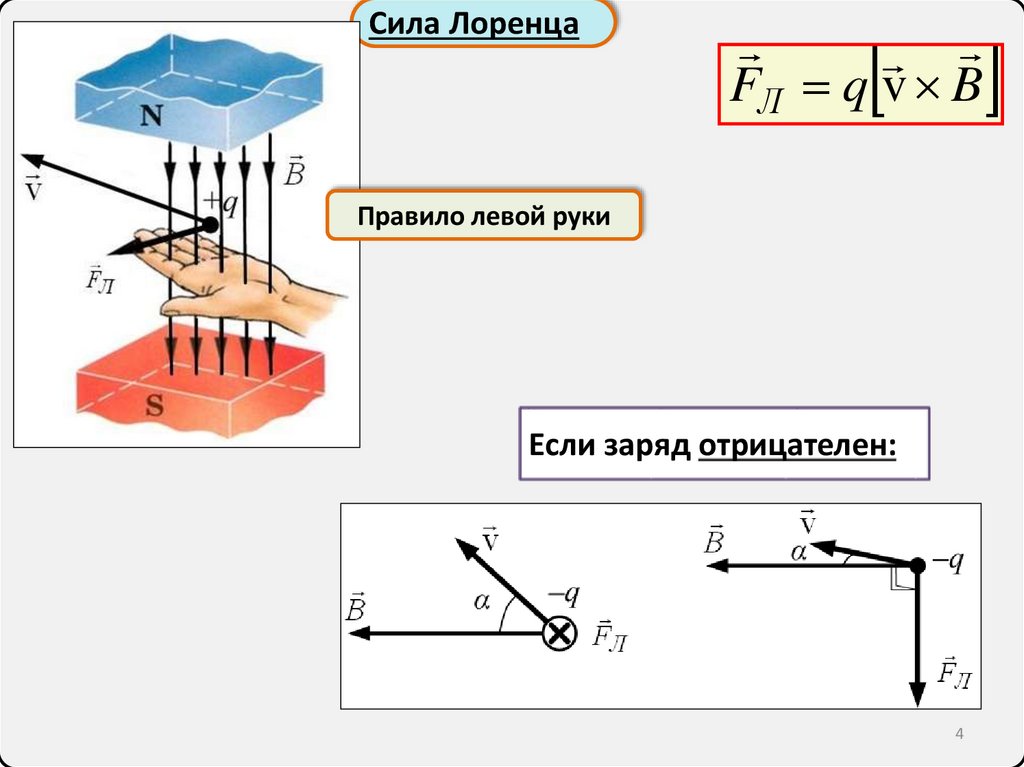
Сила Лоренца
FЛ q v B
Правило левой руки
Если заряд отрицателен:
4

5.

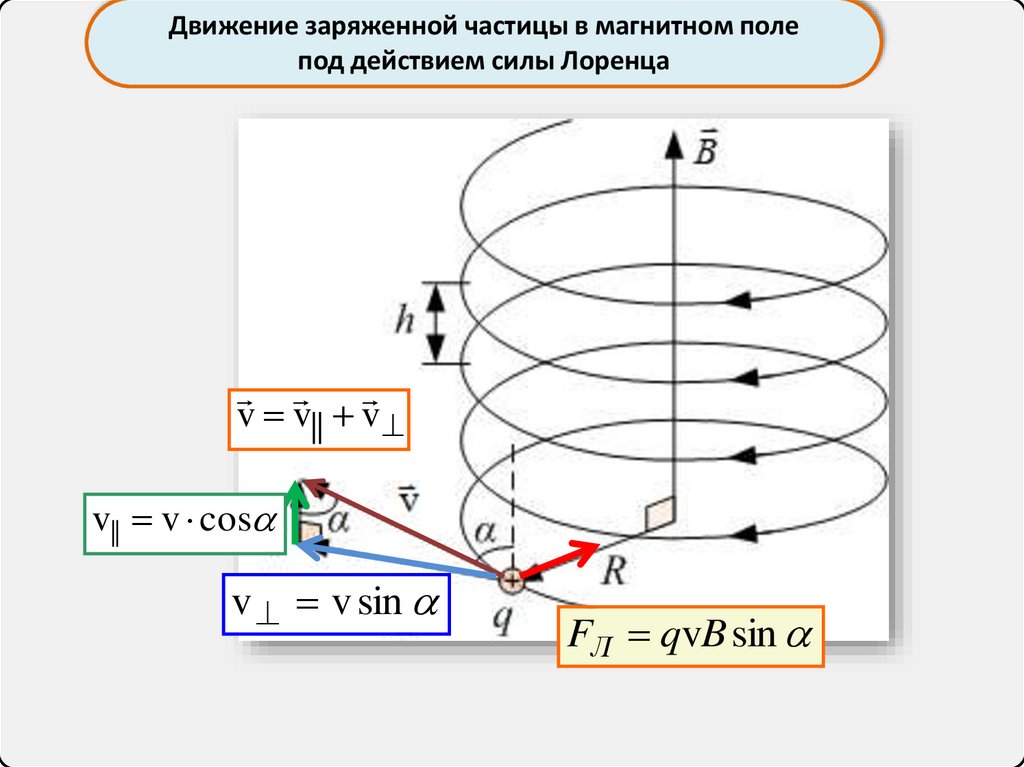
Движение заряженной частицы в магнитном поле
под действием силы Лоренца
v v|| v
v|| v cos
v v sin
FЛ qvB sin

6.

1. Вращение по окружности:
FЛ . m aц.с.
FЛ qvB sin qv B
q v B m
m v
R
q B
v v sin
v 2
R
2 R 2 mv 2 m
T
v v qB
qB
2. Равномерное поступательное
движение вдоль линий поля
2 m
h v|| T v||
qB
v|| v cos
6

7.

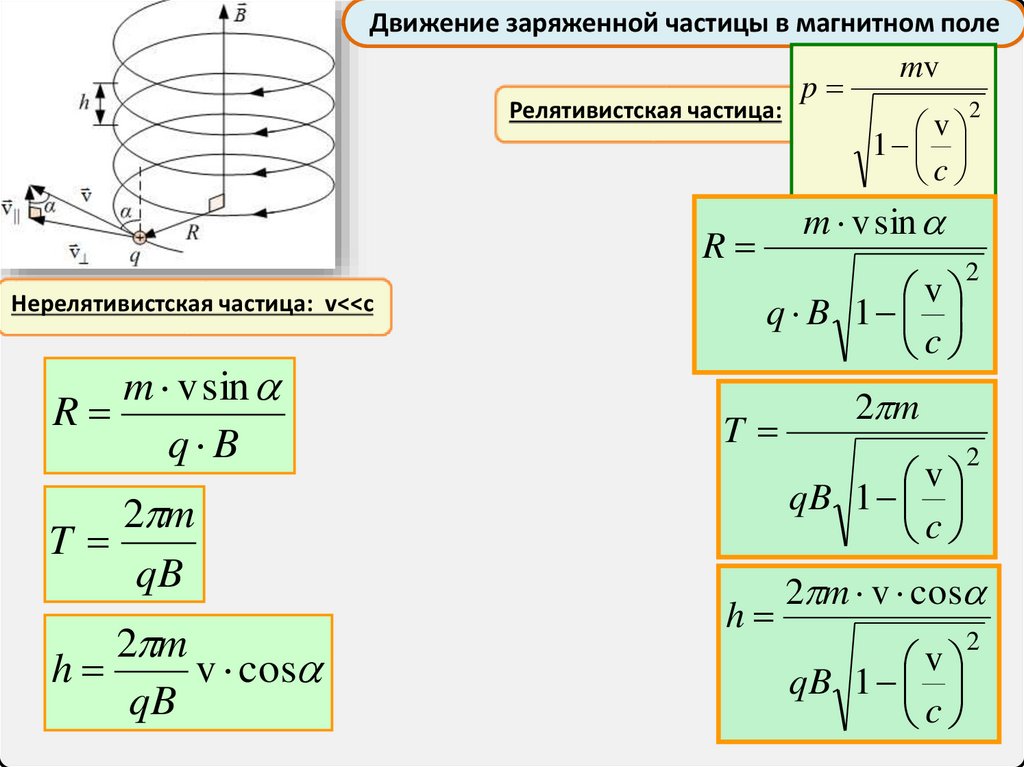
Движение заряженной частицы в магнитном поле
Релятивистская частица:
m v sin
R
q B
2 m
T
qB
2 m
h
v cos
qB
v
1
c
2
m v sin
R
Нерелятивистская частица: v<<c
p
mv
v
q B 1
c
T
2 m
v
qB 1
c
h
2
2
2 m v cos
v
qB 1
c
2

8.

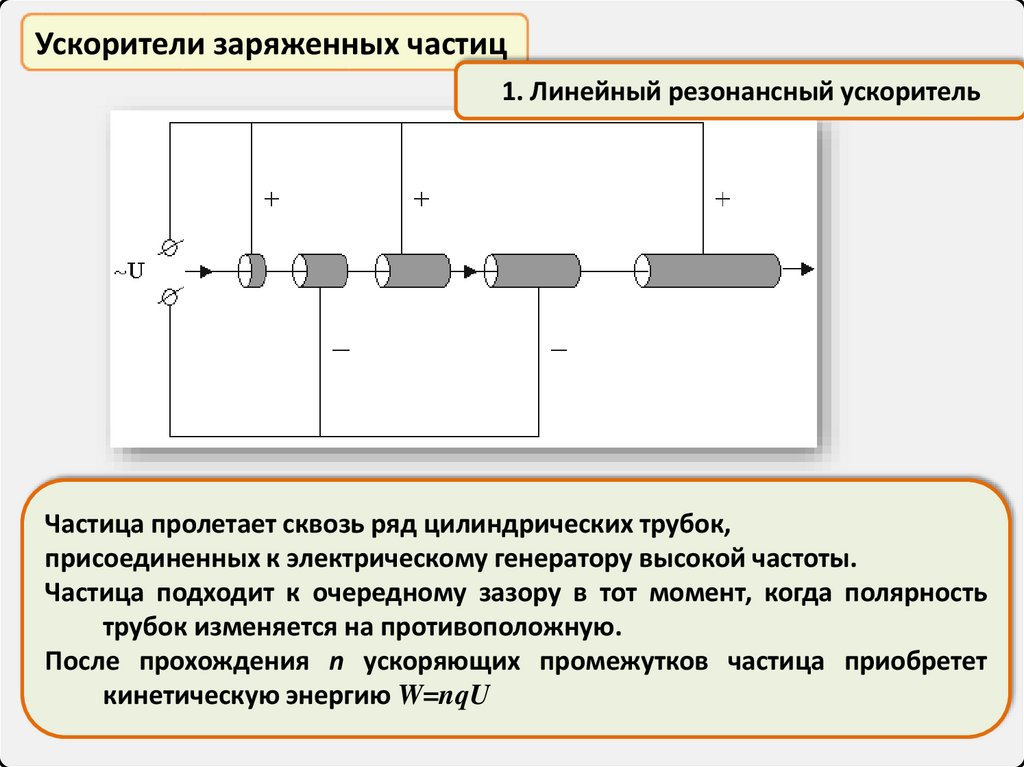
Ускорители заряженных частиц
1. Линейный резонансный ускоритель
Частица пролетает сквозь ряд цилиндрических трубок,
присоединенных к электрическому генератору высокой частоты.
Частица подходит к очередному зазору в тот момент, когда полярность
трубок изменяется на противоположную.
После прохождения n ускоряющих промежутков частица приобретет
кинетическую энергию W=nqU

9.

Ускорители заряженных частиц
1. Линейный резонансный ускоритель
Наибольший линейный ускоритель был построен в Стэнфорде, США.
Длина около 3 км
Ускорял как электроны, так и позитроны до энергии 50 ГэВ

10.

Ускорители заряженных частиц
2. Циклотрон

11.

2. Циклотрон
Условие синхронности при
v<<c
2
2 m
0
qB
U U 0 cos 0 t
При релятивистских скоростях период начинает зависеть от скорости
Для соблюдения условия синхронности меняют либо частоту ω0
(фазотрон) ,
либо индукцию В магнитного поля (синхротрон),
либо то и другое (синхрофазотрон)

12.

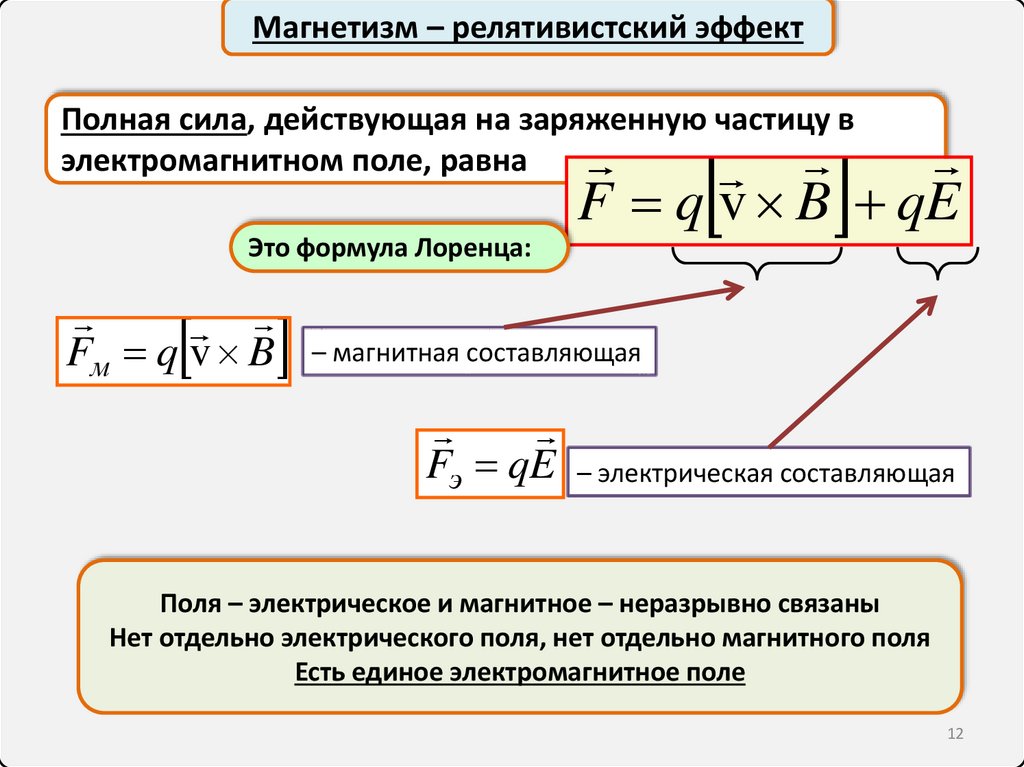
Магнетизм – релятивистский эффект
Полная сила, действующая на заряженную частицу в
электромагнитном поле, равна
F q v B qE
Это формула Лоренца:
Fм q v B
– магнитная составляющая
Fэ qE
– электрическая составляющая
Поля – электрическое и магнитное – неразрывно связаны
Нет отдельно электрического поля, нет отдельно магнитного поля
Есть единое электромагнитное поле
12

13.

Магнетизм – релятивистский эффект
К-система отсчёта:
Пример:
К’-система отсчёта
движется вместе с электроном
v
Электрон летит
параллельно
проводу
Действует магнитная составляющая силы
Лоренца
Электрон
неподвижен
На неподвижный электрон сила
Лоренца не действует
Сила не может исчезнуть, если мы перешли к другой системе отсчёта
Объяснение силы другое, но сила не исчезла
13

14.

К’-система отсчёта
v
Из-за релятивистского сокращения
длины проводник стал короче:
Движется провод
v2
l l0 1
l0
2
c
Концентрация положительных ионов в проводнике больше →
проводник заряжен положительно
Электрон притягивается к проводнику → действует электрическая
составляющая силы Лоренца Fэ
Сила не исчезла, изменилось лишь наше её описание: в одной системе
отсчёта на электрон действовало магнитное поле тока,
в другой – электрическое поле заряженного проводника
14

15.

Формулы преобразования векторов электромагнитного поля при
переходе из системы отсчёта К в систему отсчёта К’
К-система отсчёта: E и B
К’-система отсчёта: E и B
- скорость К’ относительно К
E|| E||
B|| B||
1
E c B
E
2
1
c
1
B c E
B
2
1
c
15

16.

Сила Ампера
Правило левой руки:
dFA I dl B
dFA I dl B sin
I dl
dFA I dl
Для отрезка прямого провода в однородном поле:
– элемент тока
dFA B
FA I l B
16

17.

Взаимодействие параллельных токов
I dl2
dF2 I 2 dl2 B1 sin 900
0 I1 I 2
dF2
dl2
2 d
dF2 0 I1 I 2
dl2
2 d
0 I1
B1
2 d
dF1 0 I1 I 2
dl1
2 d
dF1 dF2
- сила, действующая на единицу длины
второго провода
17

18.

В СИ единица силы тока - 1 ампер
dF 0 I1 I 2
dl
2 d
1 А – это ток, который, протекая по двум
параллельным проводникам, расположенным на
расстоянии 1м друг от друга в вакууме, вызывает
действие силы F=2.10-7 Н на каждый метр длины
проводника
Расчёт магнитной постоянной μ0
F 0 I 2
l
2 d
2 10 7 Н 0 1м 2
1м
2 1м
0 4 10
7
Н
А2
Размерность:
0
Н
Дж
Вт с В А с В с
Вб
Гн А Гн
2
2
2
2
м А м А м А
м
А
м А
м А
м А
18

19.

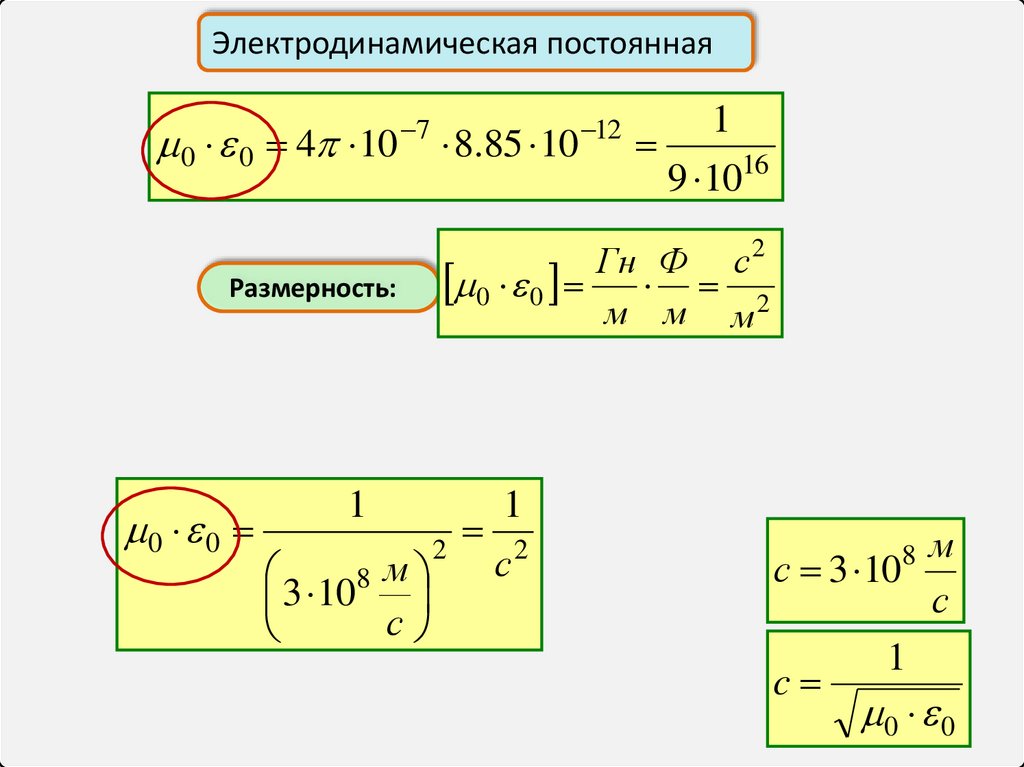
Электродинамическая постоянная
0 0 4 10
7
Размерность:
0 0
8.85 10
1
9 1016
Гн Ф с 2
0 0 2
м м м
1
8 м
3 10
с
12
2
1
с
2
м
с 3 10
с
1
c
0 019
8

20.

Рамка с током в однородном магнитном поле
F1 F2 F I a B sin 900
d b sin
Момент пары сил:
- пара сил
– плечо пары
pm
M F d I а b B sin I S B sin
M pm B sin
M pm B
20

21.

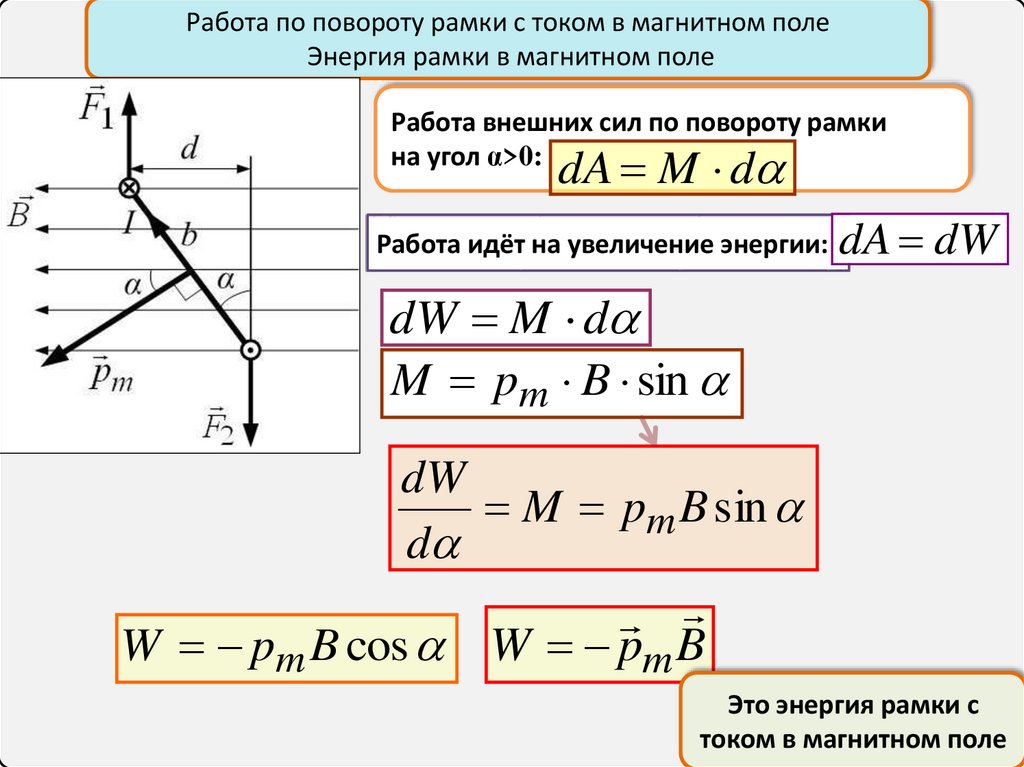
Работа по повороту рамки с током в магнитном поле
Энергия рамки в магнитном поле
Работа внешних сил по повороту рамки
на угол α>0:
dA M d
Работа идёт на увеличение энергии:
dA dW
dW M d
M pm B sin
dW
M pm B sin
d
W pm B cos W pm B
Это энергия рамки с
током в магнитном 21
поле

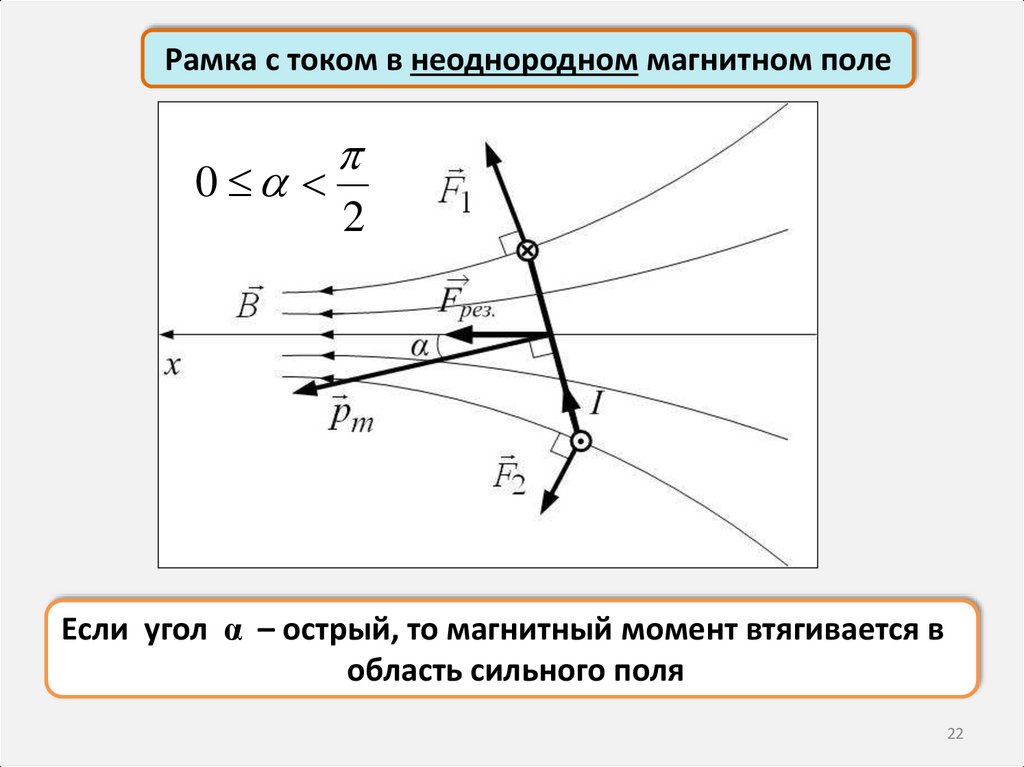
22.

Рамка с током в неоднородном магнитном поле
0
2
Если угол α – острый, то магнитный момент втягивается в
область сильного поля
22

23.

Рамка с током в неоднородном магнитном поле
2
Если угол α – тупой, то магнитный момент выталкивается
из области сильного поля
23

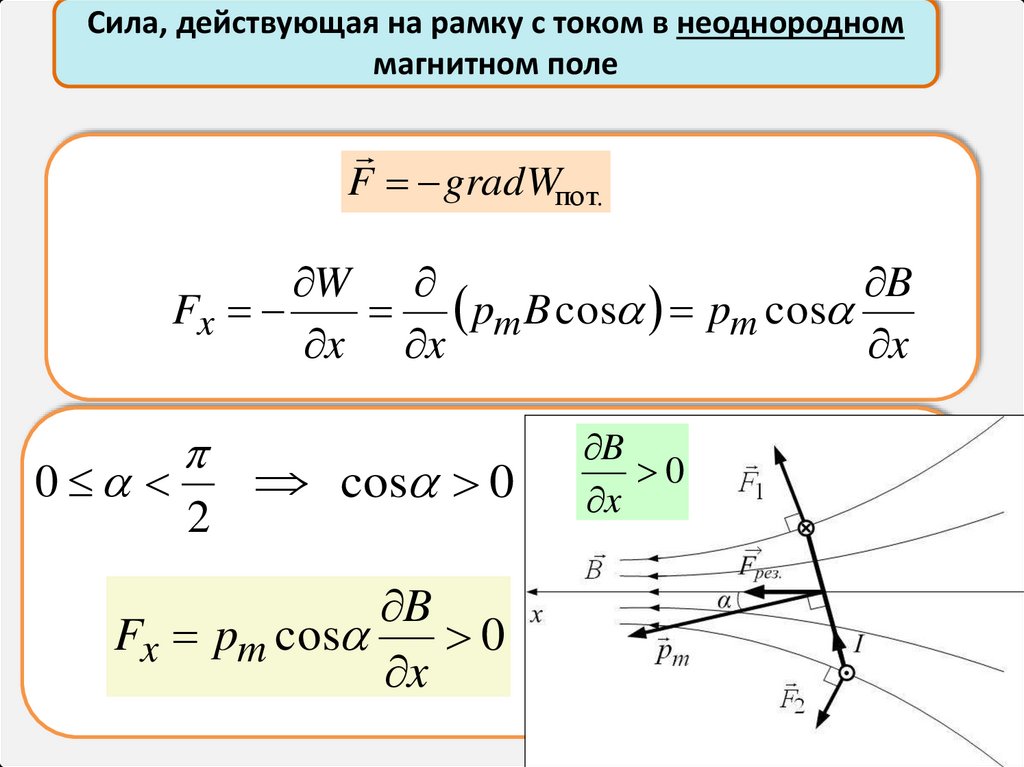
24.

Сила, действующая на рамку с током в неоднородном
магнитном поле
F gradWпот.
W
B
Fx
pm B cos pm cos
x x
x
0
2
cos 0
B
0
x
B
Fx pm cos
0
x
24

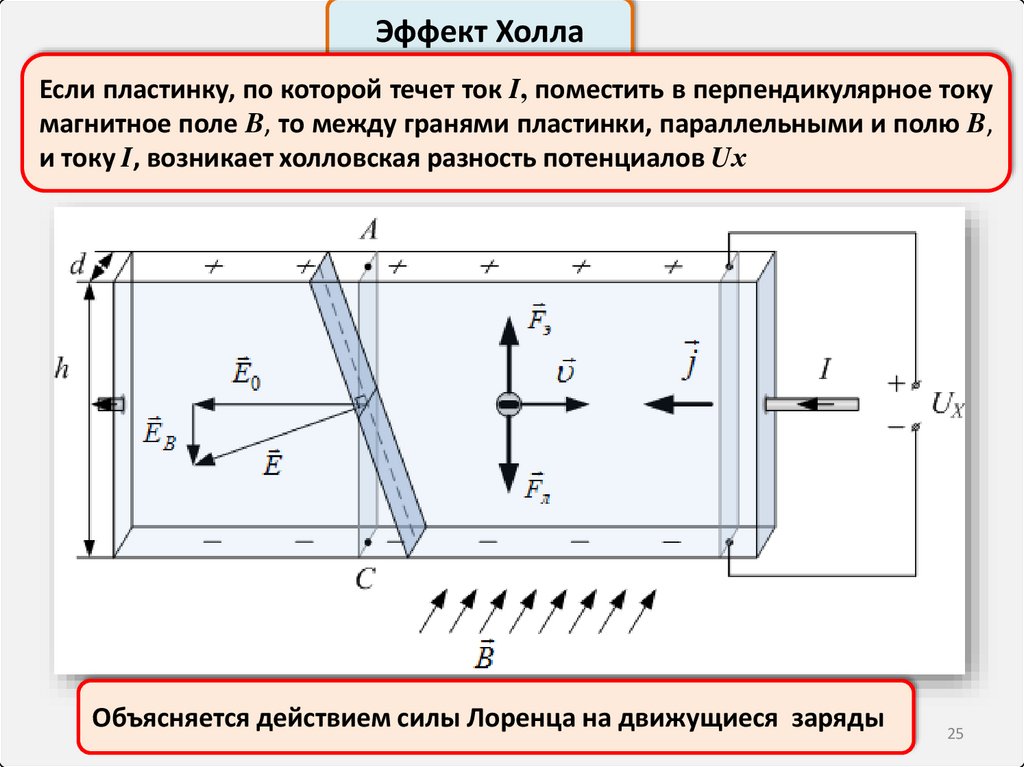
25.

Эффект Холла
Если пластинку, по которой течет ток I, поместить в перпендикулярное току
магнитное поле B, то между гранями пластинки, параллельными и полю B,
и току I, возникает холловская разность потенциалов Uх
Объясняется действием силы Лоренца на движущиеся заряды
25

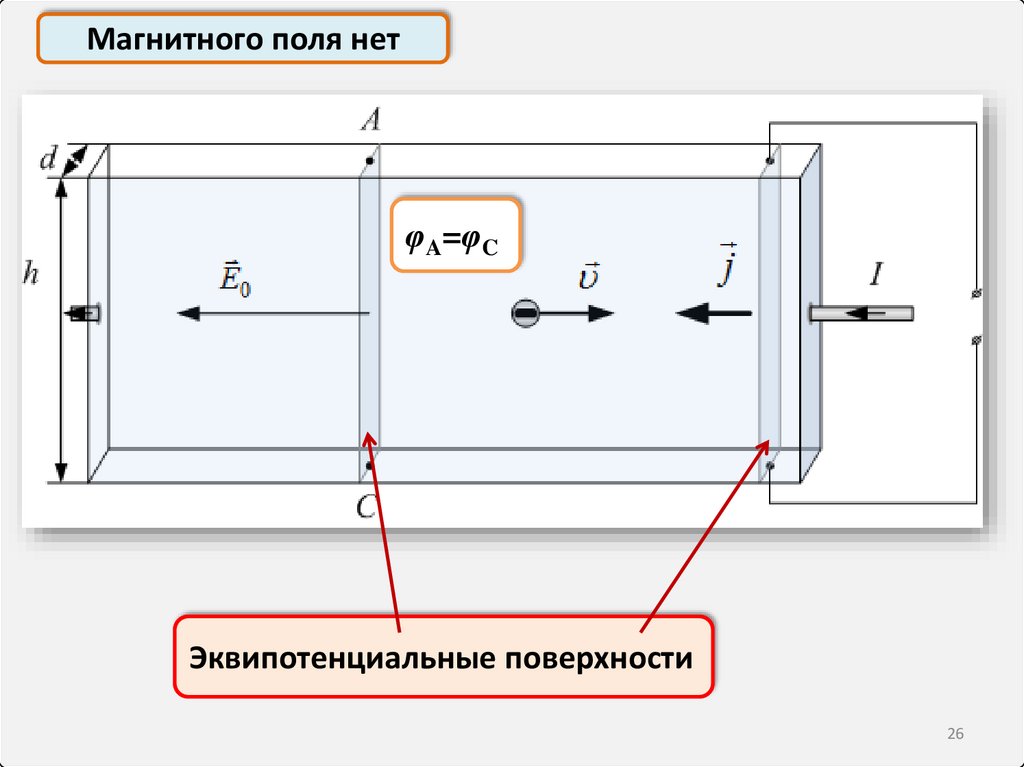
26.

Магнитного поля нет
φA=φC
Эквипотенциальные поверхности
26

27.

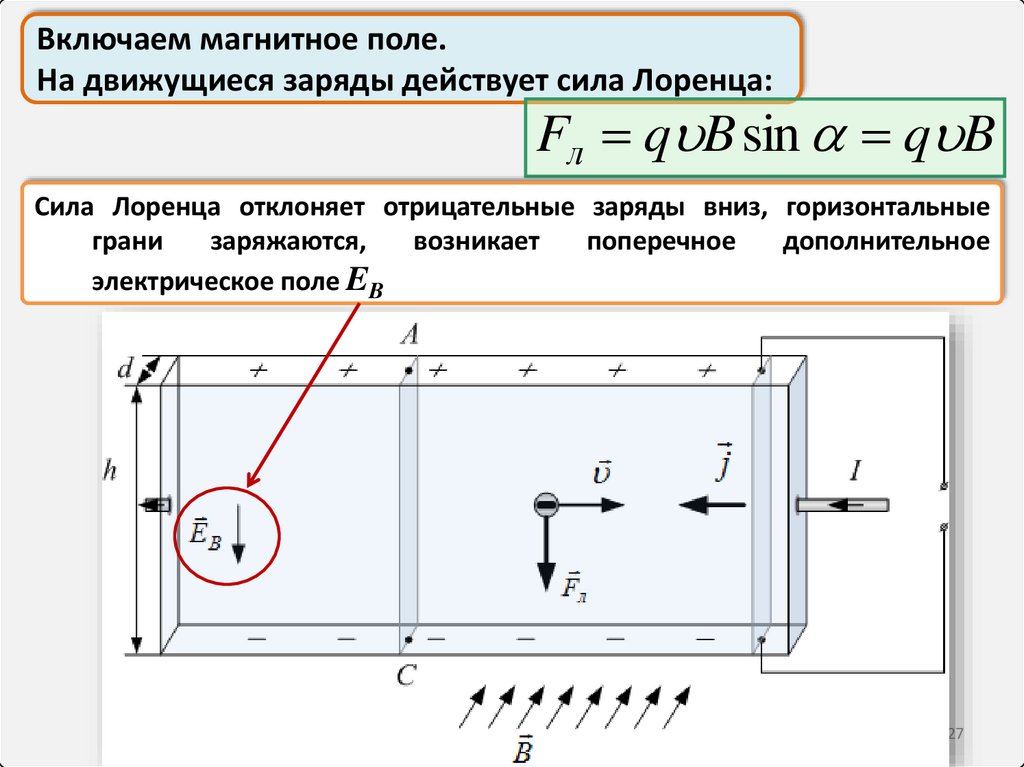
Включаем магнитное поле.
На движущиеся заряды действует сила Лоренца:
Fл q B sin q B
Сила Лоренца отклоняет отрицательные заряды вниз, горизонтальные
грани
заряжаются,
возникает
поперечное
дополнительное
электрическое поле EB
27

28.

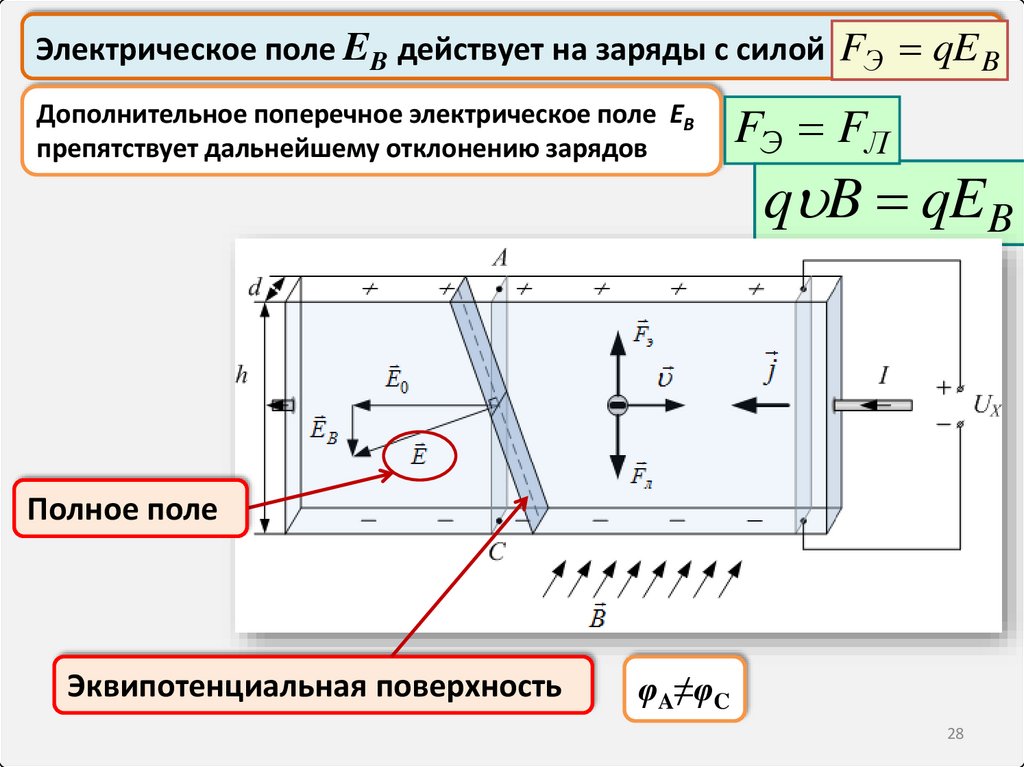
Электрическое поле EB действует на заряды с силой FЭ qE B
Дополнительное поперечное электрическое поле EB
препятствует дальнейшему отклонению зарядов
FЭ FЛ
q B qEB
Полное поле
Эквипотенциальная поверхность
φA≠φC
28

29.

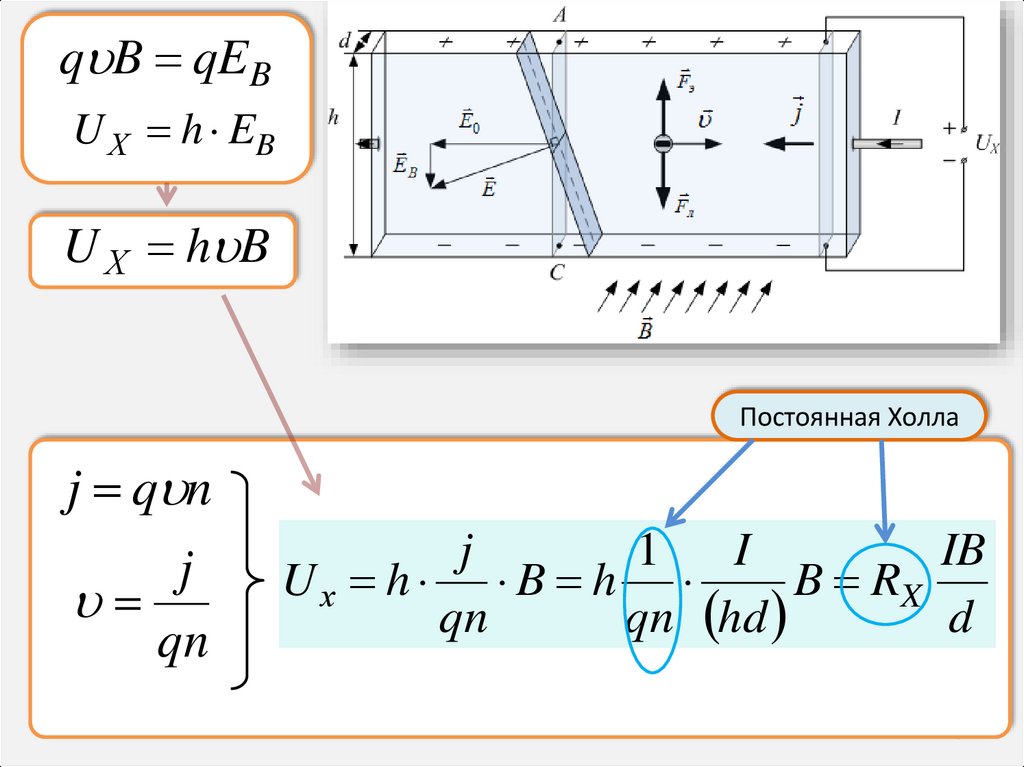
q B qEB
U Х h EB
U Х h B
Постоянная Холла
j q n
j
qn
j
1
I
IB
Uх h B h
B RX
qn
qn hd
d
29

30.

Поток вектора магнитной индукции
d B dS B dS cos Bn dS
d B dS Bn dS
S
S
S
Размерность:
Физический
смысл:
Тл м
2
Вб
Магнитный поток численно равен числу линий
магнитной индукции, пронизывающих площадку
30

31.

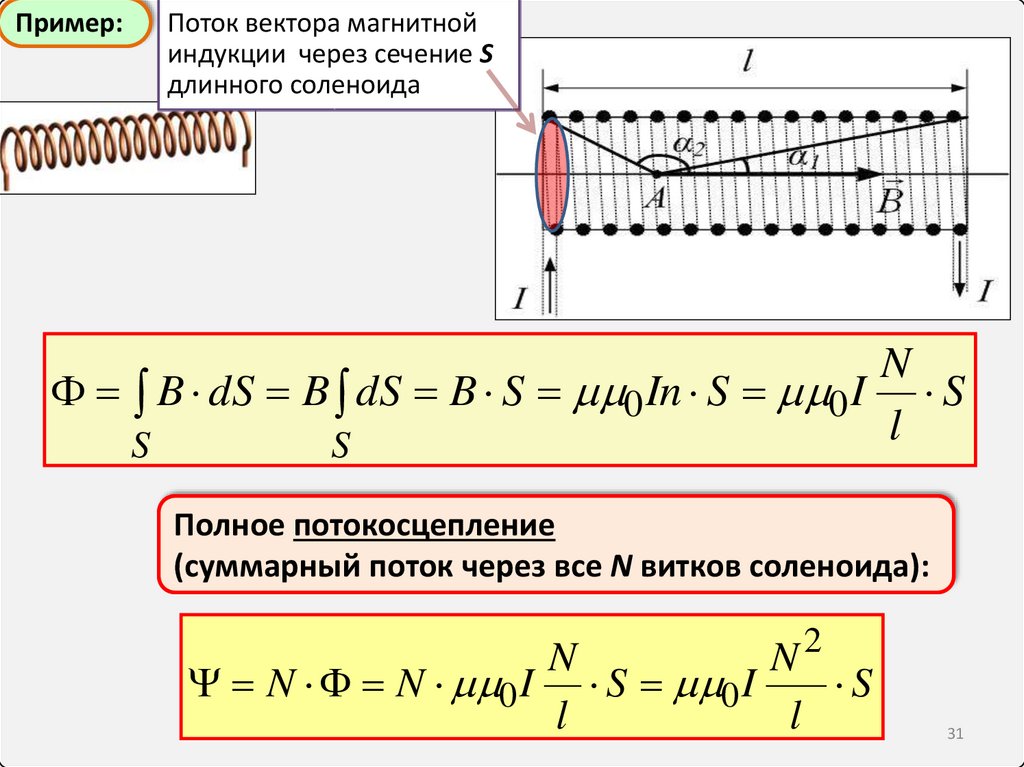
Пример:
Поток вектора магнитной
индукции через сечение S
длинного соленоида
N
B dS B dS B S 0 In S 0 I S
l
S
S
Полное потокосцепление
(суммарный поток через все N витков соленоида):
N
N2
N N 0 I S 0 I
S
l
l
31

32.

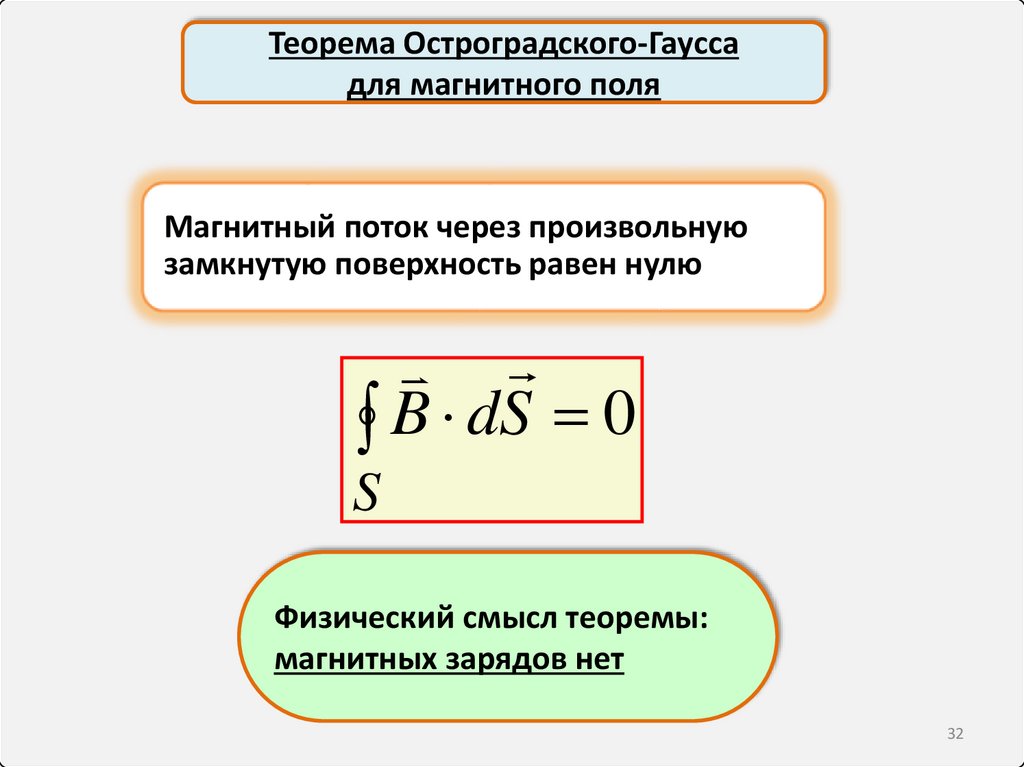
Теорема Остроградского-Гаусса
для магнитного поля
Магнитный поток через произвольную
замкнутую поверхность равен нулю
B dS 0
S
Физический смысл теоремы:
магнитных зарядов нет
32

33.

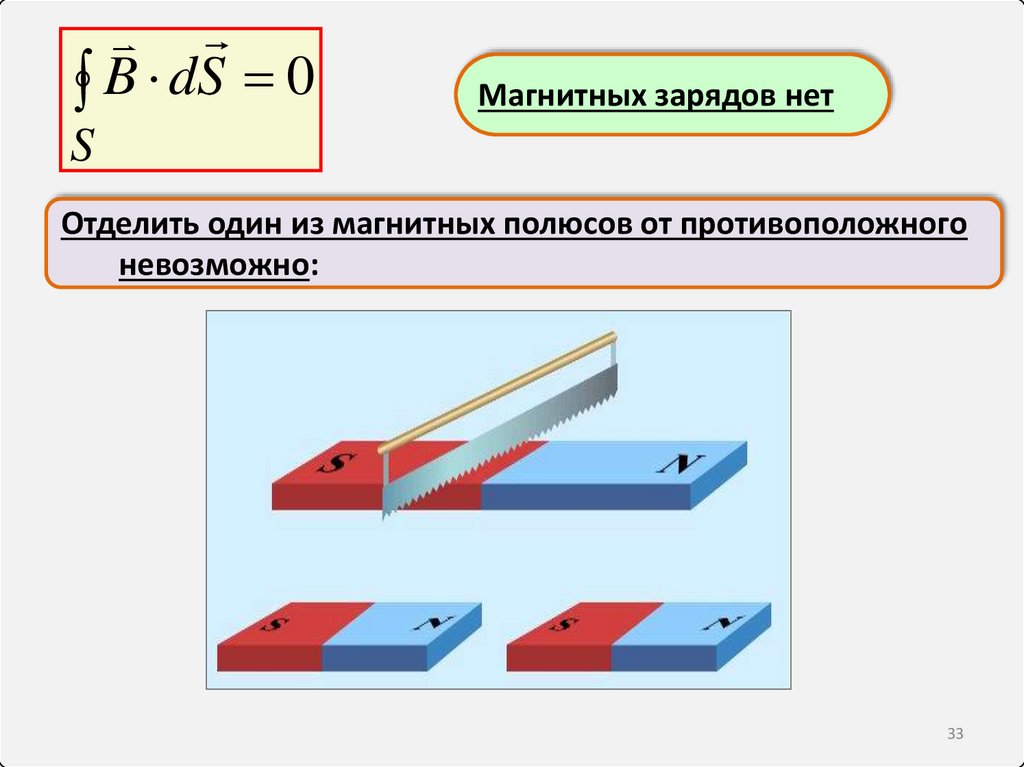
B dS 0
Магнитных зарядов нет
S
Отделить один из магнитных полюсов от противоположного
невозможно:
D dS qi
S
i
33

34.

B dS 0
Магнитных зарядов нет
S
Для сравнения теорема Гаусса для электростатического поля:
D dS qi
S
i
Отдельные тела можно зарядить либо только положительно, либо
только отрицательно,
поскольку существуют элементарные заряженные частицы – носители
электрических зарядов двух разных видов
Отсутствуют экспериментальные доказательства того, что в природе могут
существовать отдельные магнитные заряды (монополи), подобные
электрическим.
В отличие от электрических зарядов свободных магнитных “зарядов” в
природе не существует.
Нет их и в полюсах постоянных магнитов.
Поэтому линии магнитной индукции не могут обрываться на полюсах 34

35.

Работа по перемещению
проводника с током
в магнитном поле
Работа силы Ампера:
dA FA dh
dA I l B dh
l dh dS
dA I B dS
dA I d
Если ток не меняется:
A I