Similar presentations:
Высшая математика. Глава 1. Элементы линейной алгебры. Лекция 1
1. Высшая математика Глава I. Элементы линейной алгебры
ЛЕКЦИЯ 1Матрицы и
определители
2. 2. Определители
3.
Вильгельм ГотфридЛейбниц
(1646-1716) — саксонский
философ, логик, математик,
механик, физик, юрист,
историк, дипломат,
изобретатель и языковед.
Понятие «определитель»
принадлежит Г. Лейбницу
(1678).
4.
Определитель (детерминант) –числовая характеристика квадратной матрицы.
Обозначения определителя матрицы А:
|A|, det A, .
5. Невырожденная матрица
• Квадратная матрица А называетсяневырожденной, если её определитель
det А 0.
• В противном случае (det А = 0) матрица
А называется вырожденной.
6. Квадратной матрице А порядка n можно сопоставить число det A, называемое ее определителем, следующим образом: 1. n = 1. А =
(a1); det A = a12. n = 2.
| A |
a11
a12
a21 a22
a11 a22 a12 a21
• Вычисление определителя 2-го порядка
иллюстрируется схемой:
Пример.
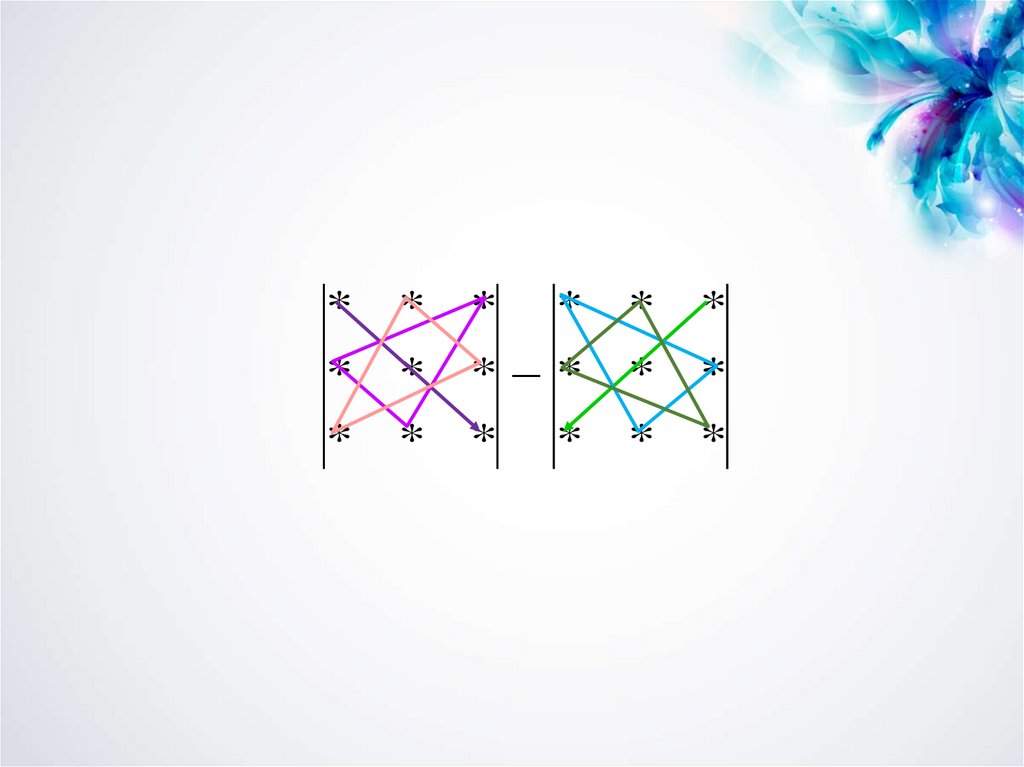
7. 3. n = 3. Для вычислении определителя 3-го порядка используют правило треугольников (Саррюса).
a11a12 a13det A a21a22 a23 a11a22 a33 a12 a23 a31
a31a32 a33
a13 a21a32 a31a22 a13 a32 a23 a11 a33 a21a12
8.
**
*
*
*
*
*
*
* *
*
*
*
*
*
*
*
*
9.
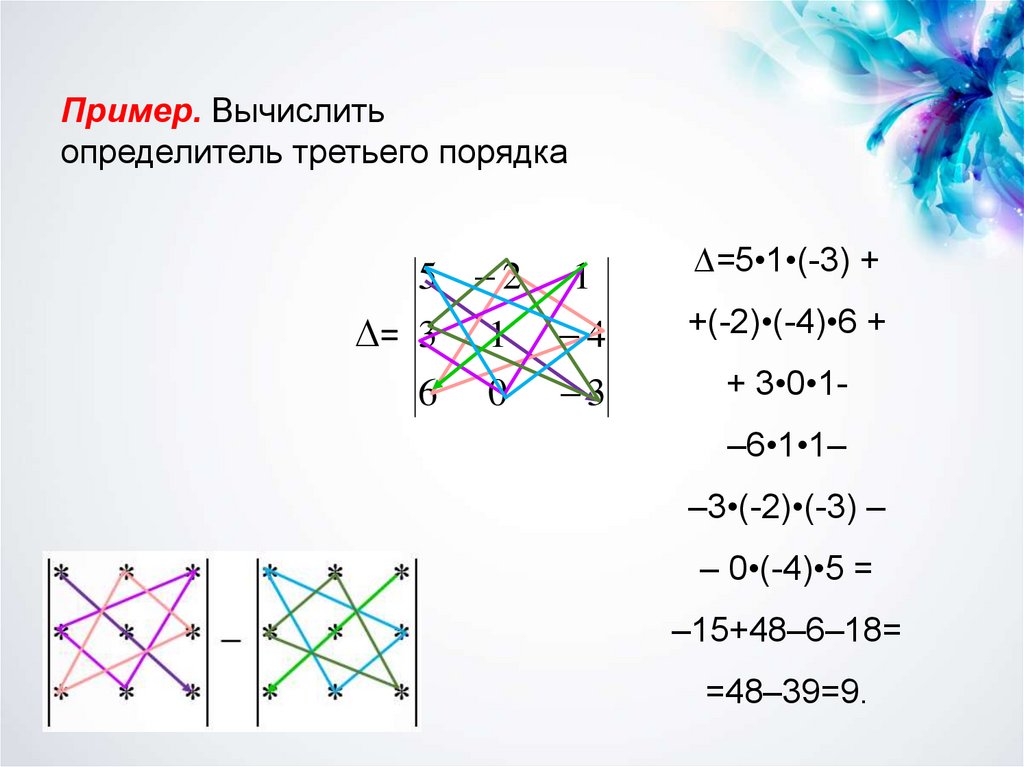
Пример. Вычислитьопределитель третьего порядка
5 2
= 3
6
1
=5•1•(-3) +
1
4
+(-2)•(-4)•6 +
0
3
+ 3•0•1–6•1•1–
–3•(-2)•(-3) –
– 0•(-4)•5 =
–15+48–6–18=
=48–39=9.
10.
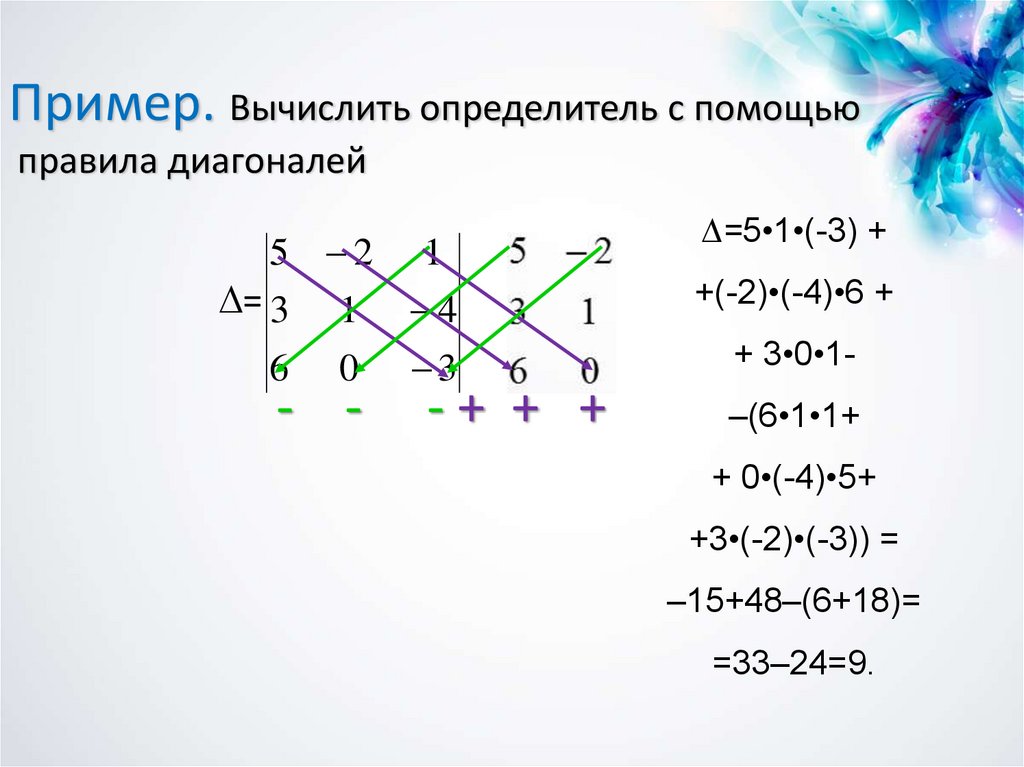
Пример. Вычислить определитель с помощьюправила диагоналей
5 2
1
=5•1•(-3) +
= 3
1
4
+(-2)•(-4)•6 +
6
0
3
+ 3•0•1-
- -
-+ + +
–(6•1•1+
+ 0•(-4)•5+
+3•(-2)•(-3)) =
–15+48–(6+18)=
=33–24=9.
11. Определитель произвольной треугольной матрицы равен произведению элементов главной диагонали
12.
Минор элемента аi j• Минором некоторого элемента aij квадратной матрицы
А n-го порядка называется определитель n –1-го
порядка матрицы, полученной из исходной путем
вычеркивания из А строки и столбца, на пересечении
которых находится выбранный элемент aij , минор
обозначается Мij.
3
7
А 0
5
2
3
5
7
5
4
6
9
a23=4
3 2 1
1
2 M23 0
2
5
4
5 2 60 20 0 250 0 42 13
7 4
M31=5
M14=11
13.
Алгебраическое дополнение Aik• Алгебраическим дополнением элемента aik
квадратной матрицы А называется число Аik :
Для предыдущего примера:
А23= –М23= –13
А31= М31= 5
А14= –М14= –11
14.
ФОРМУЛА ЛАПЛАСАТеорема. Определитель матрицы равен сумме
произведений элементов любого ее ряда на
соответствующие им алгебраические a11 a12 a13
дополнения.
a21 a22 a23
a
Разложение определителя по 31
a32
a33
элементам первой строки:
det A a 11 A11 a 12 A12 a 13 A13.
Пьер-Симо́н, маркиз де
Лапла́с (1749 - 1827) —
французский математик,
механик, физик и астроном
15.
21
2
4
3 2
11 17
11
1
12
1
1
4
3
3
4
17 12
2
1
1
17
12
2( 48 51) 2(12 17 ) 11(3 4)
6 10 11 5.
4
1
0
3
4
1
3
4 1
1 3
2 2 3 1 2 5
5
2 3 0 1
3
1
2
3
5 0 5
5 0 0 5
3
5
2
4
2(5 10 5 ( 14)) 2(50 70) 2 120 240
16. ПРАВИЛО ЧУЖИХ ДОПОЛНЕНИЙ
• Сумма произведений элементов любогоряда кв. матрицы на алгебраические
дополнения соответствующих элементов
другого ее параллельного ряда равна нулю.
17.
СВОЙСТВА ОПРЕДЕЛИТЕЛЕЙ1. Транспонирование матрицы не меняет значения ее
определителя.
det A det A
T
3 5 6
3 4 5
4 2 1 5 2 3
5 3 2
6 1 2
18.
Свойства определителей2. При перестановке двух параллельных рядов определитель
меняет знак.
3. Если соответствующие элементы двух параллельных рядов
равны или пропорциональны, то определитель равен 0.
4. Общий множитель элементов какого-либо ряда можно
вынести за знак определителя.
5. Определитель не изменится, если к элементам одного ряда
прибавить соответствующие элементы параллельного ряда,
умноженные на одно и то же число.
6. Определитель матрицы, содержащей целый ряд из нулей,
равен нулю.
7. det Е 1
8. det( A B) det A det B
19.
9. Если элементы какой-либо ряда квадратной матрицыА состоят из двух слагаемых, то определитель А равен
сумме определителей двух матриц, различающихся
между собой только элементами этого ряда, бывшими
ранее отдельными слагаемыми.
а11
а11
а 21
а 21
а31
а31
а12
а13
а 22
а 23
а32
а33
а11
а 21
а31
а12
а13
а 22
а 23
а32
а33
а11
а 21
а31
а12
а13
а 22
а 23 .
а32
а33
20.
«А математику уже затем учитьследует, что она ум в порядок
приводит».
М. В. Ломоносов
Спасибо за внимание!











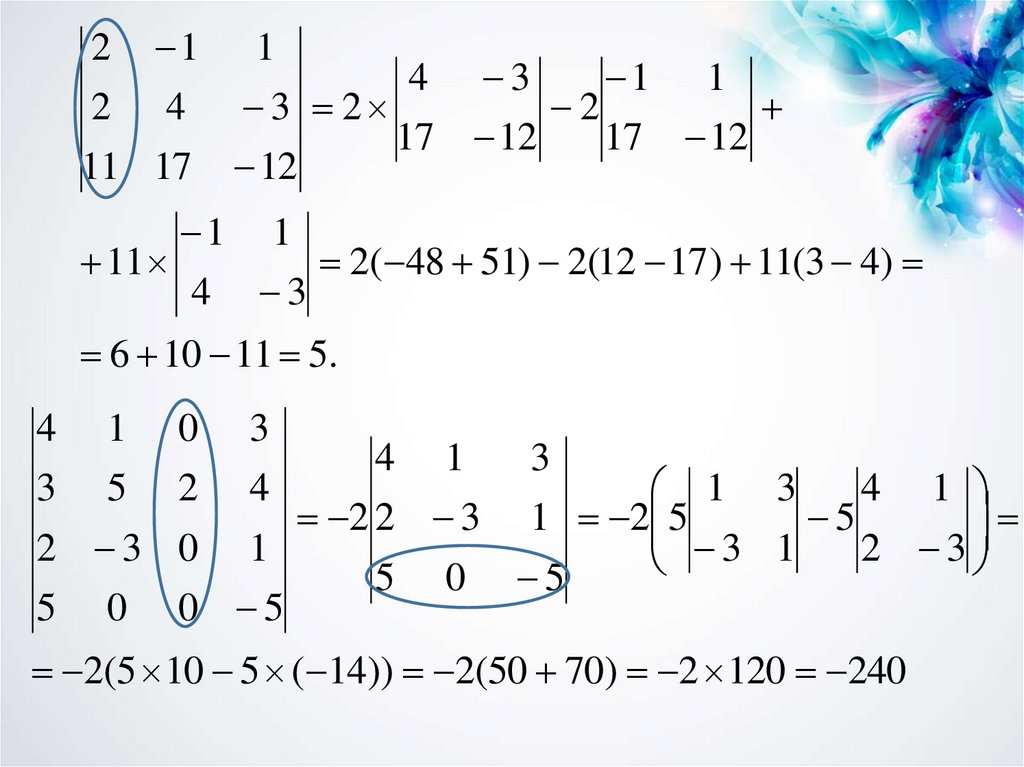





 mathematics
mathematics








