Similar presentations:
Высшая математика. Учебно-методическое пособие для подготовки к компьютерному тестированию. 1 семестр
1. Высшая математика
Лектордоцент Шинкевич Елена Алексеевна
Кафедра ВМ: ауд. 430/2
2. Литература
• Дымков М.П., Конюх А.В., МайоровскаяС.В., Петрович В.Д., Рабцевич В.А. Высшая
математика
(1
семестр):
Учебнометодическое пособие для подготовки к
компьютерному тестированию. Мн.: БГЭУ,
2011. ─ 27 с. На сайте кафедры:
http://bseu.by/hm/uchm/test/VM1.pdf
В
локальной
сети
БГЭУ:\\Arhive\UchebM\Естественнонаучные
\Высшая математика
3.
4.
5.
6. Тема 1: Элементы линейной алгебры
§1. Матрицы7. 1.1. Основные понятия
Понятие матрицы и основанный на немраздел математики – матричная алгебра
имеют важное значение для экономистов,
так как значительная часть математических
моделей экономических объектов и
процессов записывается в достаточно
простой, а главное – компактной матричной
форме.
8.
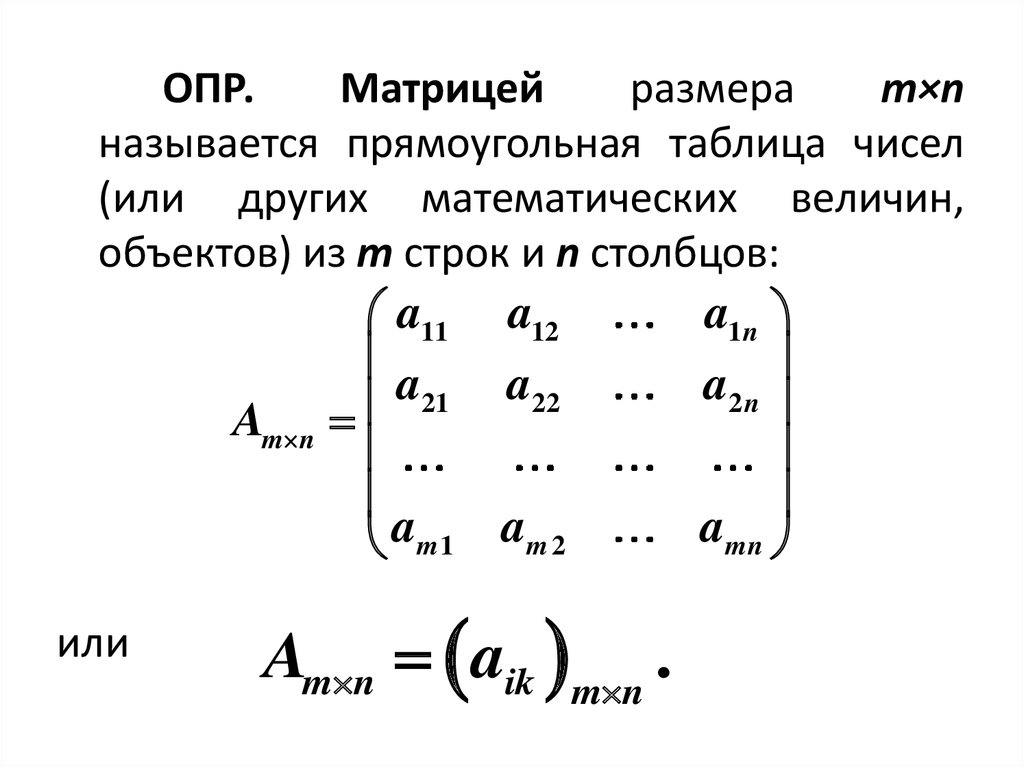
ОПР.Матрицей
размера
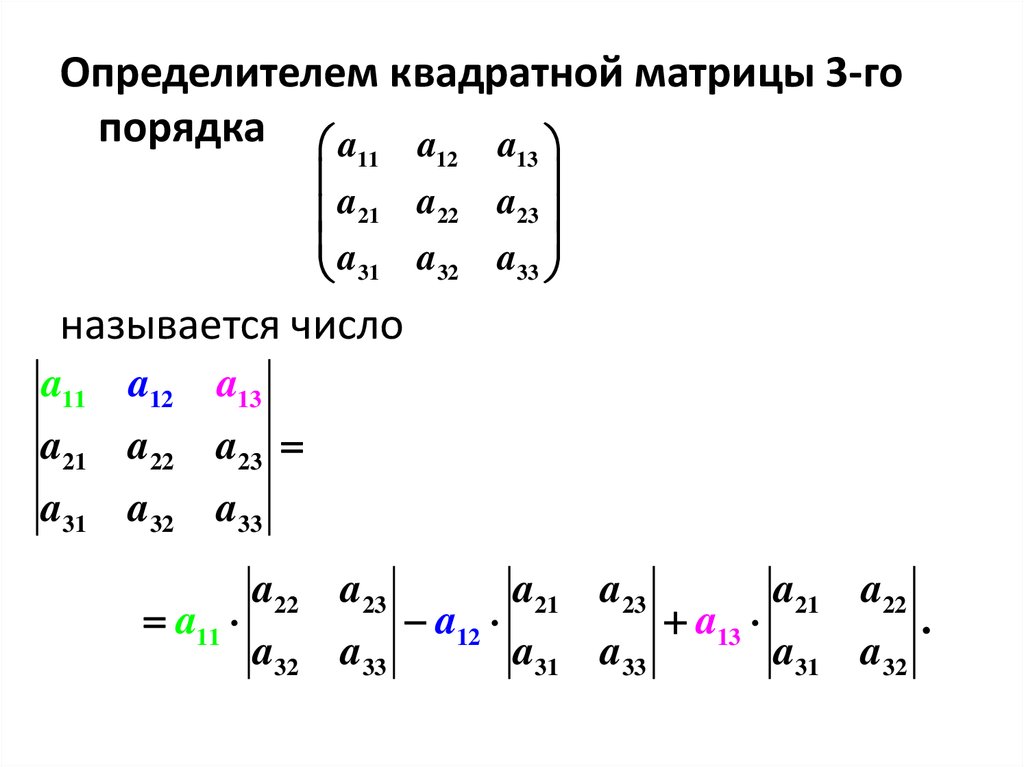
m×n
называется прямоугольная таблица чисел
(или других математических величин,
объектов) из m строк и n столбцов:
a1n
a11 a12
a
a
a
21
22
2n
Am n
amn
am 1 am 2
или
Am n aik m n .
9.
Числа,образующие
матрицу,
называются элементами матрицы: a ik –
элемент, принадлежащий i-й строке и k-му
столбцу матрицы, числа i, k называются
индексами элемента.
Матрицы обозначаются A, B, C … .
10.
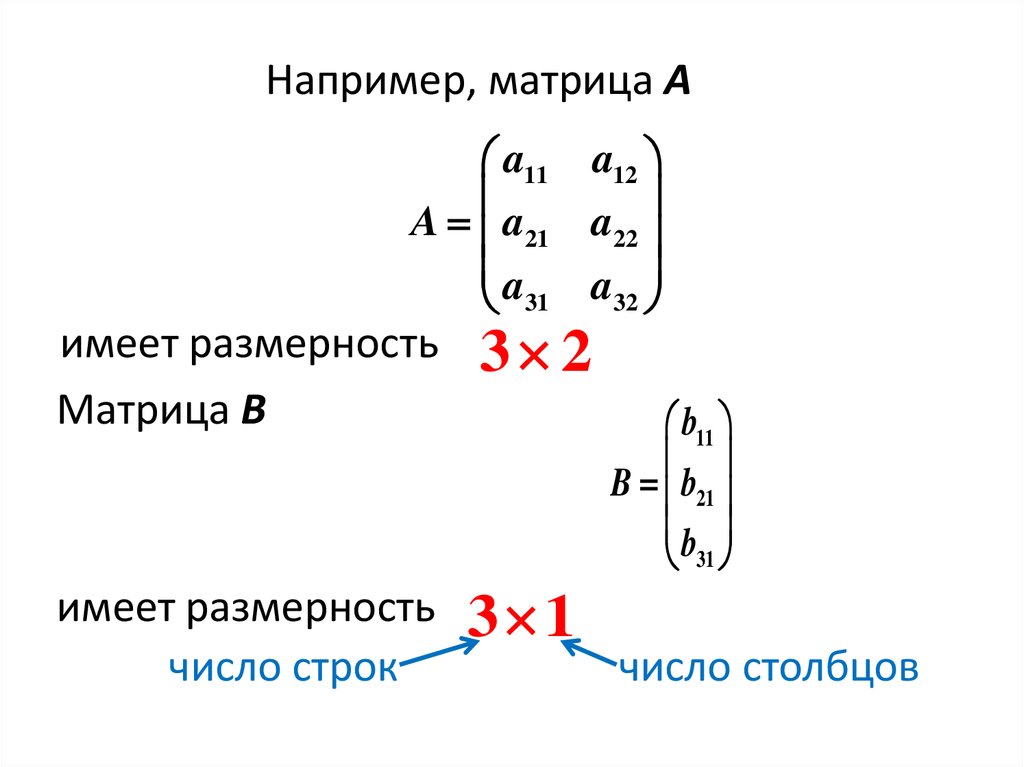
Например, матрица Aa11
A a21
a
31
a12
a22
a32
имеет размерность
Матрица B
3 2
имеет размерность
число строк
3 1
b11
B b21
b
31
число столбцов
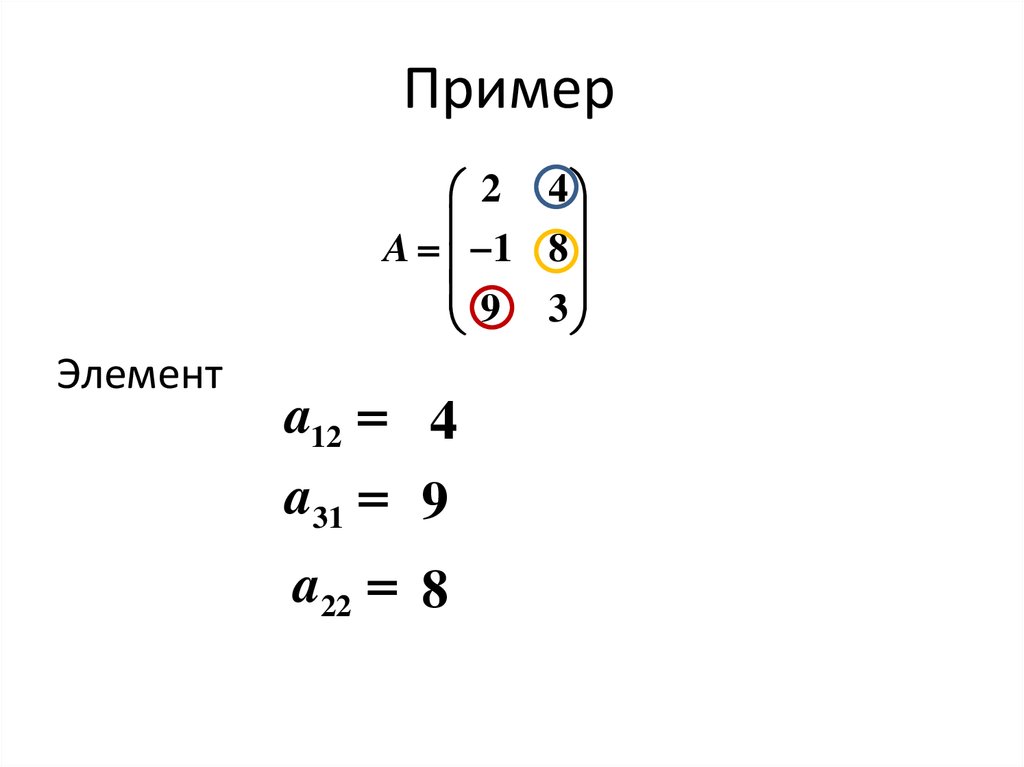
11. Пример
2 4A 1 8
9 3
Элемент
a12 4
a31 9
a22 8
12.
ОПР. Матрицы A и B одинаковыхразмеров называются равными, если
равны их соответствующие элементы:
aik bik , i 1,2,
, m, k 1,2,
,n
ОПР. Матрица, у которой все элементы
равны нулю, называется нулевой. Она
обозначается Om n .
13. Пример
Дано:Пример
2 4
2 4
C 2
A 1 8 , B 1 8 ,
1
9 3
9 3
0 0
O 0 0
0 0
4
,
8
0
0 ,
0
2 4
D 1 8 ,
9 3
Указать размерность данных матриц.
Имеются ли среди данных матриц равные?
A3 2 , B3 2 , CB2 2 , D
D3 2 , O3 3 ,
14.
ОПР. Квадратной матрицей n-го порядканазывается матрица размера
n×n.
Обозначается An .
В квадратной матрице элементы a11 , a22 , , ann
образуют главную диагональ.
15.
Матрица размерности m×1 называетсяматрицей-столбцом.
Матрица размерности 1×n называется
матрицей-строкой.
Пример.
A 2 3 1 ,
3
B 2
1
16.
ОПР. Квадратная матрица называетсядиагональной, если ее элементы на
главной диагонали не все равны нулю, а все
остальные элементы равны нулю.
ОПР. Диагональная матрица, у которой
все элементы главной диагонали равны
единице, называется единичной матрицей.
Обозначается E n .
Матрица размера 1×1, состоящая из
одного числа, отождествляется с этим
числом: A a11 a11 .
1 1
17. 1.2. Операции над матрицами
К линейным операциям над матрицамиотносятся сложение и вычитание матриц,
умножение матрицы на число.
Складывать и вычитать можно только
матрицы одинаковых размеров.
18.
ОПР. Суммой (разностью) двух матрицA aik m n и
B bik m n
называется такая матрица
C cik m n , что
cik aik bik cik aik bik ,
т. е. матрица, элементы которой равны
сумме
(разности)
соответствующих
элементов матриц A и B.
19. Пример
Найти A+B, A+C, B+C, если это возможно.1
1 2 3
A
B 3
4 0 5
2
4
7 2
C
3 4
Существует сумма B+C:
1 2 7 2
B C
3 4 3 4
1 7 2 2 8 4
3 3 4 4 0 0
20.
ОПР. Произведением матрицы A aik m n начисло (или числа на матрицу A)
называется матрица B bik m n
, для
которой
bik aik , i 1, m, k 1, n
т. е. матрица, полученная из данной
умножением всех ее элементов на число .
Обозначение A A B
21. Пример
1 2 3A
4 0 5
3 2 1
B
0 7 8
2 4 6
2A
8 0 10
5 6 5
2A B
8 7 18
22.
ОПР. ПроизведениемA B матриц
и Bn r
называется матрица C размера m r такая,
что
Am n
cij ai 1b1 j ai 2b2 j
ainbnj
т. е. элемент i-й строки и j-гo столбца
матрицы произведения cij равен сумме
произведений элементов i-й строки
матрицы A на соответствующие элементы
j-го столбца матрицы B.
23.
Операция умножения двух матрицопределяется только для случая, когда
число столбцов первой матрицы равно
числу строк второй матрицы.
Если матрицы A и B квадратные одного
размера, то произведения A B и B A
всегда существуют, но не обязательно
равны.
24. Пример
Найти произведения матриц AB и BA (еслиэто возможно):
3
1 2 3 B 5
A
1
1 0 1
3
1 2 3
A2 3 B3 1
5
1 0 1
1
1 3 2 5 3 1 16
C 2 1
1 3 0 5 1 1 2
25. Пример
Найти произведения матриц AB и BA (еслиэто возможно):
1 2 3
A
1 0 1
A2 3 B3 3
3 4 5
B 6 0 2
7 1 8
3 4 5
1 2 3
6 0 2
1 0 1
7
1
8
26.
1 я строка матрицы А прикладываетсяк первому столбцу матрицы В, соответствующие
элементы перемножаются, а произведения складываются
1 3 2 6 3 7 1 4 2 0 3 1 1 5 2 ( 2) 3 8
1 3 0 6 1 7 1 4 0 0 1 1 1 5 0 ( 2) 1 8
36 7 25
4 3 3
Произведение BA не существует, так как
число столбцов матрицы B не совпадает с
числом строк матрицы A .
27.
ОПР. Матрица, полученная из даннойзаменой каждой ее строки столбцом с тем
же номером, называется матрицей,
транспонированной относительно данной.
Матрицу,
транспонированную
относительно матрицы A, обозначают AT .
Например, если
2 2 2
A 3 3 3
5 5 5
2 3 5
T
A 2 3 5 .
2 3 5
28. Свойства
AT
A B
T
A B
T
A;
A B ;
T
T
T
B A .
T
T
29. Элементарные преобразования матриц
1. Перестановка местами двух рядовматрицы;
2. Умножение всех элементов ряда матрицы
на число, отличное от нуля;
3. Прибавление ко всем элементам ряда
матрицы соответствующих элементов
параллельного ряда, умноженных на одно
и тоже число.
Под рядом матрицы понимается строка
или столбец матрицы.
30.
ОПР. Две матрицы A и B называютсяэквивалентными, если одна из них
получается из другой с помощью
элементарных преобразований.
Записывают:
A
B.
31. §2. Определители
Любой квадратной матрице n-гопорядка A можно поставить в соответствие
число, которое называется определителем
матрицы A, и обозначается det A, A ,
A (дельта).
Определителем
1-го
порядка
квадратной матрицы A a11 называется
значение a11 : det A a .
11
32.
Определителем квадратной матрицы2-го порядка
a11 a12
A
a21
a22
называется число, равное a11 a22
обозначаемое символом
a11
a12
a21
a22
a12 a21
a11a22 a12a21 .
33. Пример
Вычислить определитель1.
2.
3
5
2 6
1 3
2
3
3 6 5 ( 2) 18 10 28.
1 3 3 2 9
34.
Определителем квадратной матрицы 3-гопорядка a a a
11
a21
a
31
12
a22
a32
13
a23
a33
называется число
a11
a21
a31
a12
a22
a32
a13
a 23
a33
a11
a22
a23
a32
a33
a12
a21
a23
a31
a33
a13
a21
a22
a31
a32
.
35. Пример
Вычислить определитель:2 1 3
4 2 5
Решение.
6
3
7
2 1 3
2 5
4 5
4 2
4 2 5 2
( 1)
3
3 7
6 7
6 3
6 3 7
2 2 7 5 3 1 4 7 5 6 3 (4 3 2 6)
2 ( 1) 1 ( 2) 3 0 2 2 4.
36.
ОПР. Минором M ij элемента aijквадратной матрицы A
n-го порядка
называется определитель (n-1)-го порядка,
полученный
из
исходного
путем
вычеркивания строки и столбца, на
пересечении
которых
находится
выбранный элемент.
ОПР. Алгебраическим дополнением Aij
элемента квадратной матрицы aij
называется произведение
i j
( 1)
Mij Aij .
37. Пример
2 1 5В матрице A 1 4 2
0 2 1
2 5
минором элемента a22 является M 22
2,
0 1
минором элемента a33 является
M 33
2
1
1 4
8 1 9.
Алгебраическое дополнение элемента a22
2 5
2 2
A22 ( 1) M 22
2.
0 1
38. §3. Обратная матрица
Пусть A — квадратная матрица n-гопорядка.
ОПР. Квадратная матрица A называется
невырожденной, если определитель detA
не равен нулю: det A 0.
В противном случае ( det A 0 ) матрица A
называется вырожденной.
39.
ОПР. Матрицей, присоединенной кматрице A aij , называется матрица
,
— алгебраическое дополнение
n n
A Aij
T
где Aij
элемента aij данной матрицы A.
1
Матрица A
называется обратной к
квадратной матрице A, если выполняется
1
1
условие A A A A E ,
где E — единичная матрица того же
порядка, что и матрица A.
40.
Матрица A 1 имеет те же размеры, чтои матрица A.
Теорема 1. Всякая невырожденная
матрица имеет обратную (и причем только
одну).
41. Алгоритм вычисления обратной матрицы
1. Находим определитель исходной матрицы.Если det A 0 , то матрица A вырожденная
и обратной матрицы не существует.
Если det A 0 , то матрица невырожденная
и обратная матрица существует.
2. Находим матрицу AT , транспонированную
к матрице А.
42.
3. Находим алгебраические дополненияэлементов транспонированной матрицы и
из них составляем присоединенную
T
матрицу A A
.
ij
4. Вычисляем обратную матрицу по
формуле:
1
1
A
det A
A.
5. Проверяем правильность вычисления
обратной матрицы
1
1
A A A A E.
43. Пример
Вычислить обратную матрицу для матрицы4 5
A
2 7
Решение. Найдем определитель:
4 5
det A
28 10 18 0
2 7
Обратная матрица существует.
44.
Присоединенная матрица имеет вид:5
7
A
2 4
Тогда обратная матрица:
1
1 7 5
A
A
det A
18 2 4
1
5
7
18
18
2
4
18
18
45.
Проверка:1
A A
4 5 1
2 7 18
7 5
2 4
1 4 7 10 20 20
18 14 14
10 28
1 18 0 1 0
18 0 18 0 1
46. §4. Матричные уравнения
Матричные уравнения простейшеговида
с
неизвестной
матрицей
X
записываются следующим образом
AX B,
XA B.
В этих уравнениях A, B, X ― матрицы
таких размеров, что все используемые
операции умножения возможны, и с обеих
сторон от знака равенства находятся
матрицы одинаковых размеров.
47.
Если в уравненияхAX B, XA B
матрица A невырожденная, то их решения
записываются следующим образом
Если AX B, то X A 1 B,
Если
XA B
то
1
X BA .
48. Пример
• Решить матричное уравнение:1 1
2 3
X
2 3
1 4
Решение. Запишем данное матричное
уравнение в виде AX B . Его решением
1
является матрица
(если
X A B
существует матрица A 1 ).
Найдем обратную матрицу.
1) Найдем определитель матрицы :
49.
det A1
1
2
3
1 0
Значит, обратная матрица существует, и
исходное уравнение имеет единственное
решение.
1
1 3 1 3 1
A
A
.
det A
1 2 1 2 1
1
Запишем решение уравнения:
3 1 2 3 5 5
X A B
.
2 1 1 4 3 2
1
50. Ранг матрицы
Рассмотрим матрицу размера m×n.Выделим в ней k строк и k столбцов,
k min{m; n}
Из элементов, стоящих на пересечении
выделенных строк и столбцов, составим
определитель k-го порядка. Все такие
определители называются минорами этой
матрицы и обозначаются M k .
51.
ОПР. Рангом матрицы A называетсянаивысший порядок отличного от нуля
минора матрицы.
Обозначают: rank ( A).
Очевидно, что 0 rank ( A) min{m; n}.
























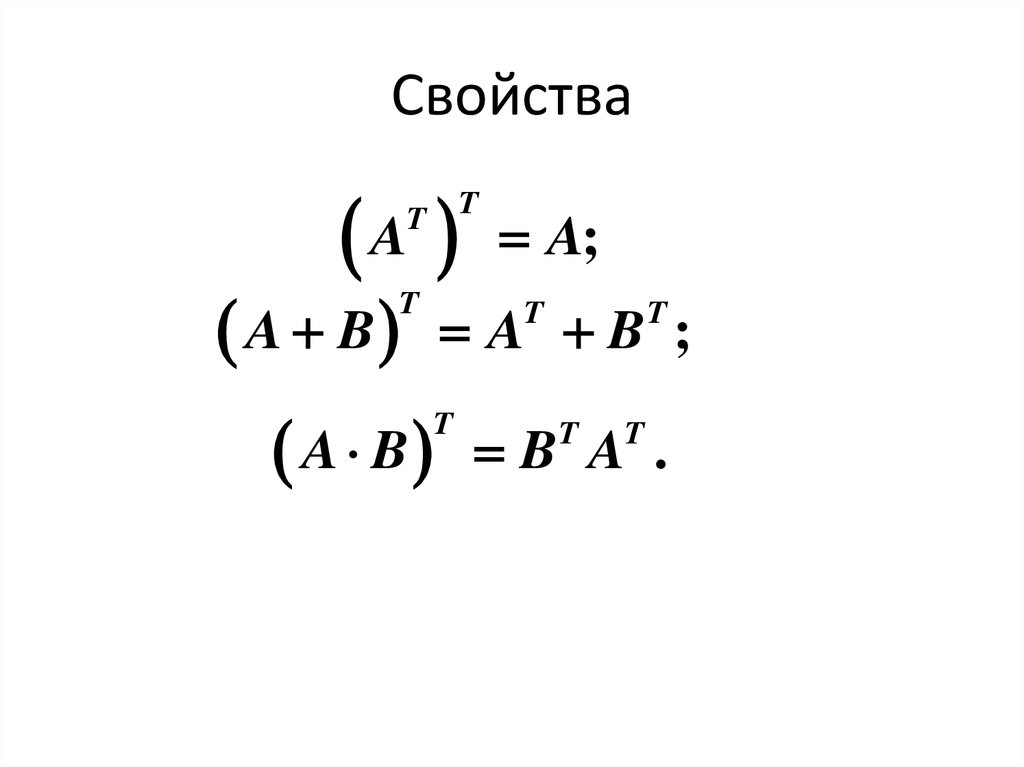















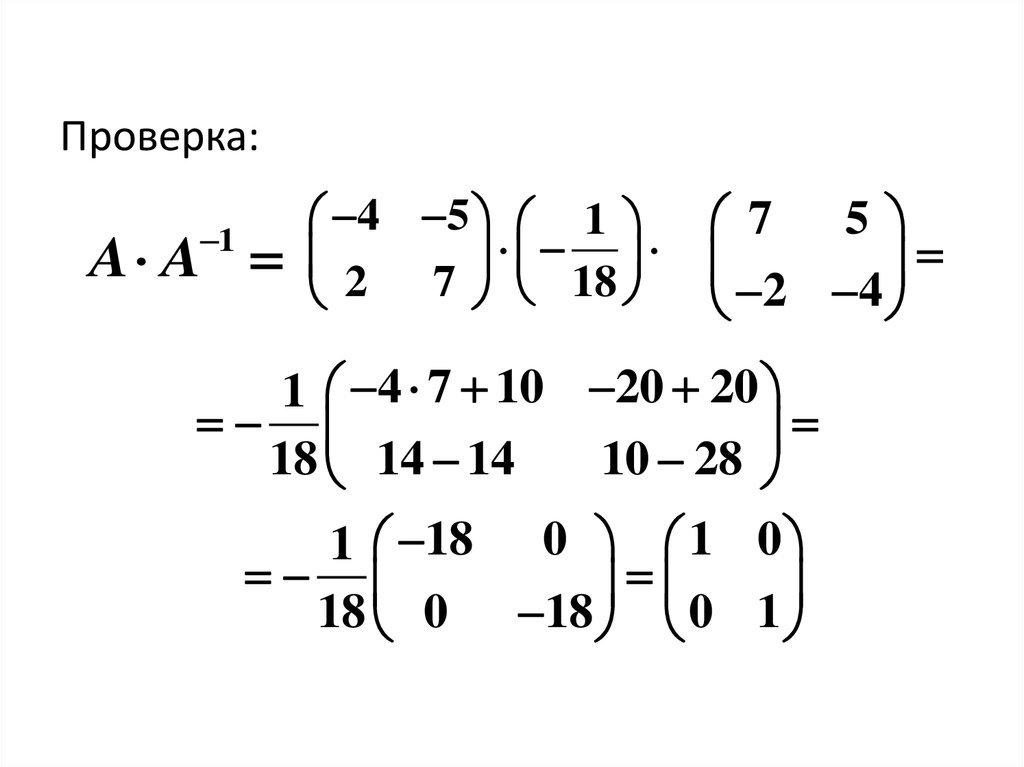






 mathematics
mathematics








