Непрерывность функции в точке и на числовом промежутке. Свойства непрерывных функций

1.

Тема 8. «Непрерывность функции в точке и на числовом промежутке.
Свойства непрерывных функций».
1.Определение непрерывности функции в точке.
2.Определение функции непрерывной в интервале, на отрезке.
3. Точки разрыва и их классификация.
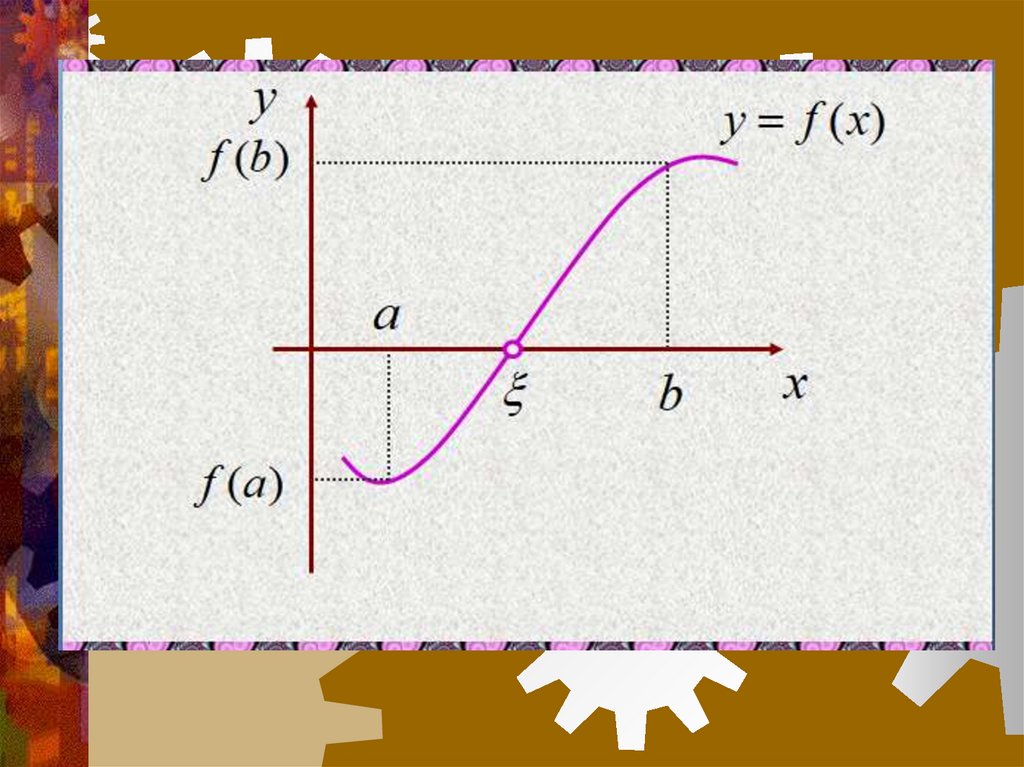
4. Свойства функций, непрерывных на отрезке.

2.

Функция f(x) называется непрерывной в
точке x0, если она определена в этой
точке (т.е. существует значение
функции в этой точке f(x0)) и имеет
конечный предел при
x x0
равный значению функции в этой точке:
lim f ( x) f ( x0 )
x x0

3.

1
Функция
1
y
x
не является непрерывной в точке х=0, т.к. не
существует значения функции в этой точке:
1
y (0)
0

4.

2
Функция
x 1, x 0
y
x 1, x 0
существует в точке х=0 , т.к. у(0)=1
Рассмотрим пределы этой функции в точке х=0 .
Предел слева:
lim ( x 1) 1
x 0 0
Предел справа:
lim ( x 1) 1
x 0 0
Эти пределы неравны, следовательно общего
предела не существует и функция не является
непрерывной в этой точке.

5.

3
Функция
y x
2
является непрерывной в точке х=0, т.к.
существует значение функции в этой точке:
y(0)=0
и существует предел
lim x 0
2
x 0

6.

Определение непрерывности функции может
быть записано в виде:
lim f ( x) f (lim x)
x x0
x x0

7.

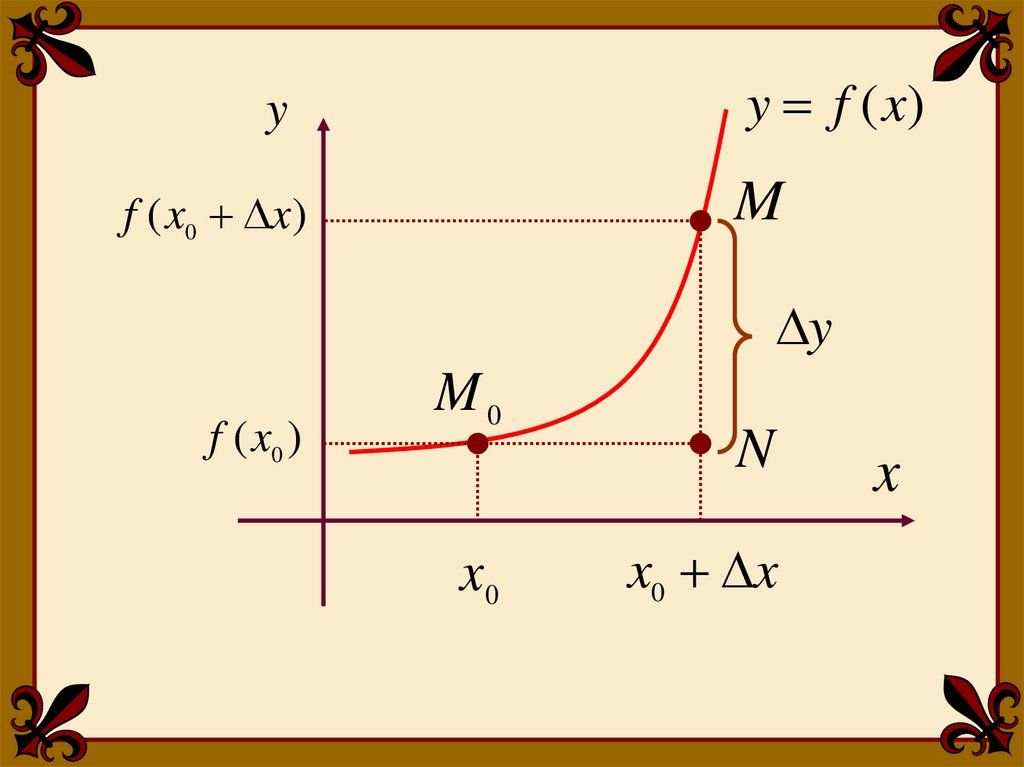
Непрерывность функции в данной точке
выражается непрерывностью графика при
прохождении этой точки.
Рассмотрим график функции y=f(x).
Дадим аргументу x0 приращение Δx. Тогда
функция получит приращение Δy:
y f ( x0 x) f ( x0 )
Графически:

8.

y f (x)
y
M
f ( x0 x)
y
f ( x0 )
M0
x0
N
x0 x
x

9.

Функция f(x) называется непрерывной в
точке x0, если она определена в точке x0
и бесконечно малому приращению
аргумента соответствует бесконечно
малое приращение функции:
lim y 0
x 0

10.

Точка x0 называется точкой разрыва
функции f(x), если в этой точке функция
не является непрерывной.

11.

Точки разрыва бывают 1 и 2 рода.
Точка x0 называется точкой разрыва первого
рода функции f(x), если существуют
односторонние пределы функции слева и
справа при x x0
Точка x0 называется точкой разрыва второго
рода функции f(x), если хотя бы один из
односторонних пределов функции равен
бесконечности или не существует.

12.

1
Функция
1
y
x
имеет точку разрыва второго рода
поскольку:
1
lim
x 0
x
х=0,

13.

2
Функция
x 1, x 0
y
x 1, x 0
имеет точку разрыва первого рода
поскольку:
lim ( x 1) 1
x 0 0
lim ( x 1) 1
x 0 0
х=0,

14.

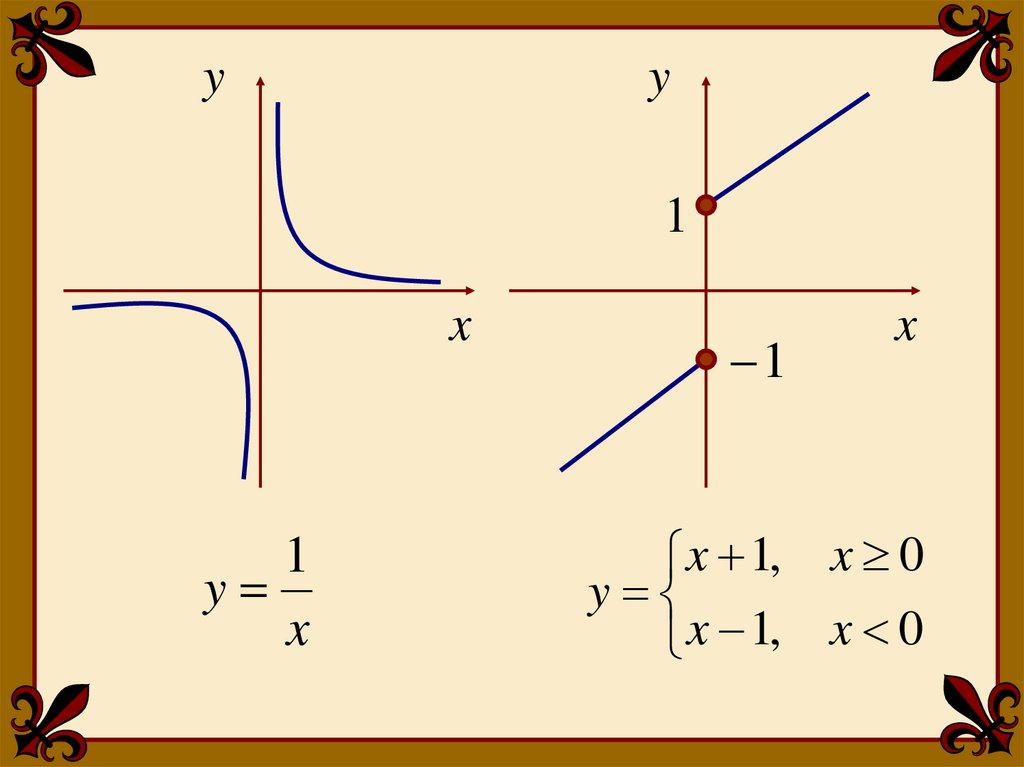
y
y
1
x
1
y
x
1
x
x 1, x 0
y
x 1, x 0

15.

1
тоже являются функциями, непрерывными в точке x0.