Similar presentations:
Решение иррациональных неравенств
1. Решение иррациональных неравенств.
2.
10 а класс (09.11.2021)Учитель: Чернова Т.В.
Тема
Решение иррациональных неравенств
Инструкция
Сегодня начнем тему «Решение иррациональных неравенств».
Скопируйте эту технологическую карту к себе на рабочий стол и выполняйте
задания, которые прописаны в алгоритме занятия.
Обучающимся (5чел), которые прислали решения трудных примеров, выставлены
пятерки в сетевой город за 08.11.21. Решения присланы оперативно. По этим
записям должны были разобрать решения обучающиеся, которые не смогли решить
уравнения самостоятельно.
Алгоритм
занятия
1.
1.
2.
3.
Комментари
й
09.11.2021
Учебное занятие на платформе «Сферум» 30 минут.
(разбор части теории по решению неравенств, используя
презентацию).
Презентация будет прикреплена в сетевом городе, так как по ней организован
следующий этап работы.
Работа с презентацией: конспект примеров, разобранных на платформе
«Сферум», и оставшихся примеров для самостоятельного изучения на уроке
09.11.21 по презентации.
Маленькое домашнее задание № 16.2 (1) 16.4 (4) 16.6(3)
Если у меня не получится связаться с вами на платформе «Сферум» или занятие
сорвется, то разберете презентацию самостоятельно. Методы решения неравенств
похожи на методы решения уравнений.
2
3.
Рассматрим решение неравенств, содержащихпеременную под знаком квадратного корня.
При решении таких неравенств необходимо помнить условие
существования квадратного корня (ОДЗ): подкоренное
выражение не может принимать отрицательные значения.
Некоторые методы решения иррациональных
неравенств.
Назад
Метод интервалов.
Использование равносильных переходов.
Введение новой переменной.
Метод рационализации (замены множителей).
Использование свойств квадратного корня.
Решение неравенств, содержащих двойные радикалы.
4.
Некоторые методы решения иррациональныхнеравенств.
Использование равносильных переходов.
5.
МетодыИспользование равносильных переходов.
Выведем схемы решения трех основных типов иррациональных
неравенств используя свойства числовых неравенств и здравый смысл.
Таким образом избежим малоэффективного механического
запоминания.
f(x) 0
ОДЗ
:
1. a ) f ( x ) g( x )
g( x ) 0
Так как левая и правая части неравенства
неотрицательны, то по свойству числовых
неравенств имеем право возвести их в квадрат
не меняя при этом знак неравенства.
То есть, необходимо f ( x ) 0
выполнение трех
g( x ) 0
f ( x ) g( x )
условий:
f ( x ) g( x )
Найди лишнее!
f(x) 0
f0( x f)( x ) gg((xx))
f ( –xлишнее
) g( x )
Очевидно, что g(x) ≥0
5
6.
Использование равносильных переходов.Методы
Самостоятельно выведи схему для решения следующего неравенства
1. б )
f ( x ) g( x )
f ( x) 0
g ( x) 0
f ( x) g ( x)
f(x) 0
ОДЗ :
g( x ) 0
f ( x ) g( x )
( x– )лишнее
0
g≥0
0 f g( (xx))
f (gx() x=>
f(x)
)
f ( x ) g( x )
Следует отметить, что данные переходы справедливы и для
нестрогих неравенств.
6
7.
• Пример №1Из учебника пример 1 страница 123,
записать решение в тетрадь
(попробовать решить самостоятельно, а
затем проверить по учебнику)
09.11.2021
7
8.
Использование равносильных переходов.2.
f ( x ) g( x )
ОДЗ : f ( x ) 0
Условие, при котором неравенство
может иметь решения: g ( x ) 0
2
Тогда: f ( x ) g ( x )
Незначительно отличается
переход для нестрогого
неравенства:
Методы
f(x) 0
f ( x ) g( x ) g( x ) 0
f ( x ) g2( x )
f(x) 0
f ( x ) g( x ) g( x ) 0
f ( x ) g2( x )
8
9.
МетодыИспользование равносильных переходов.
Переходы
Пример 2.
x( 2 x ) 0
2 x x 2 0
x 5
2 x x 2 5 x 5 x 0
2 x 2 12 x 25 0
2 x x 2 ( 5 x )2
2 x 2 12 x 25 0
x 5
x( 2 x ) 0
2 x 2 12 x 25 0
D 0 функция не имеет нулей
0
2
2 x 2 12 x 25 0
5
x R
Ответ : [ 0 ;2 ]
при любом х
10.
• Решение примера 2 из учебника стр 123• (попробовать решить самостоятельно, а
затем проверить по учебнику)
09.11.2021
10
11.
Использование равносильных переходов.3.
f ( x ) g( x )
Методы
ОДЗ : f ( x ) 0
Решения у такого неравенства могут быть при любом значении g(x)
1 случай: g ( x ) 0
f(x) 0
Тогда неравенство выполнено при любом х ϵ ОДЗ
g( x ) 0
2 случай: g ( x ) 0
f(x) 0
Тогда имеем право возвести обе части в квадрат g ( x ) 0
f ( x ) g2( x )
f ( x ) 0
g( x ) 0
f ( x ) g( x )
g( x ) 0
2
f ( x ) g ( x )
11
12.
МетодыИспользование равносильных переходов.
Переходы
Пример 3.
x 2 2 x 1 0
2 x 3 0
2
x 2x 1 2x 3
2 x 3 0
x 2 2 x 1 ( 2 x 3 )2
1 система
x 2 2 x 1 0
2 x 3 0
( x ( 1 2 ))( x ( 1 2 )) 0
x 1,5
1 2
1,5
1 2
x [ 1 2 ;1,5 )
12
13.
Использование равносильных переходов.Методы
Переходы
Пример 3.
x [ 1 2 ;1,5 )
2
x 2 x 1 2 x 3 2 x 3 0
x 2 2 x 1 ( 2 x 3 )2
2 система
2 x 3 0
2
2
x 2 x 1 ( 2 x 3 )
x 1,5
x 2 ( x 0 ,8 ) 0
Объединение решений
0 ,8
1,5
2
x [ 1,5 ;2 )
x [ 1 2 ;1,5 )
x [ 1,5 ;2 )
Ответ : [ 1 2 ;2 )
14.
• Решение примера 3 из учебника стр 124• (попробовать решить самостоятельно, а
затем проверить по учебнику)
09.11.2021
14
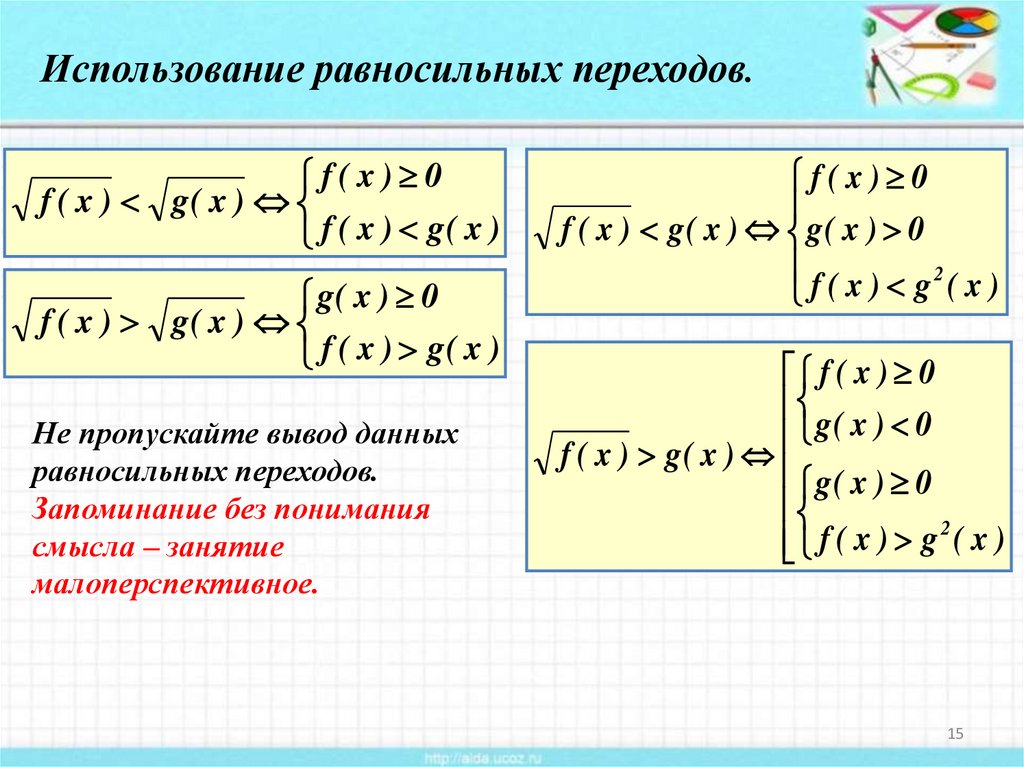
15.
Использование равносильных переходов.f(x) 0
f ( x ) g( x )
f ( x ) g( x )
g( x ) 0
f ( x ) g( x )
f ( x ) g( x )
Не пропускайте вывод данных
равносильных переходов.
Запоминание без понимания
смысла – занятие
малоперспективное.
f(x) 0
f ( x ) g( x ) g( x ) 0
f ( x ) g2( x )
f ( x ) 0
g( x ) 0
f ( x ) g( x )
g( x ) 0
2
f ( x ) g ( x )
15
16.
УРОК за 9 ноябрязакончен!!!
Домашнее задание:
Прочитать теоремы о равносильности неравенств
( учебник стр. 122-123)
Решить примеры №16.2 (1), 16.4(4), 16.6 (3)
09.11.2021
16
17.
Учебное занятиена 10 ноября
(смотрите технологическую карту
на 10 ноября в сетевом городе)
09.11.2021
17
18.
Запишите тему:Введение новой переменной.
19.
Метод введения новой переменной(явная замена).
Пример 1. 2 x 3 x 1 0
2 t 2 3t 1 0
2( t 0 ,5 )( t 1 ) 0
ОДЗ : x 0
t x x t2
0 ,5
1
1 ) x 1 - правая и левая части неравенства
x 1
неотрицательны => имеем право
x 0 ,5
возвести в квадрат x 1
1
1
1
- аналогично x . С учетом ОДЗ 0 x .
2) x
2
4
4
t 1
t 0 ,5
Ответ: объединение решений
первого и второго неравенства.
Ответ : [ 0 ;0 ,25 ] [ 1; )
20.
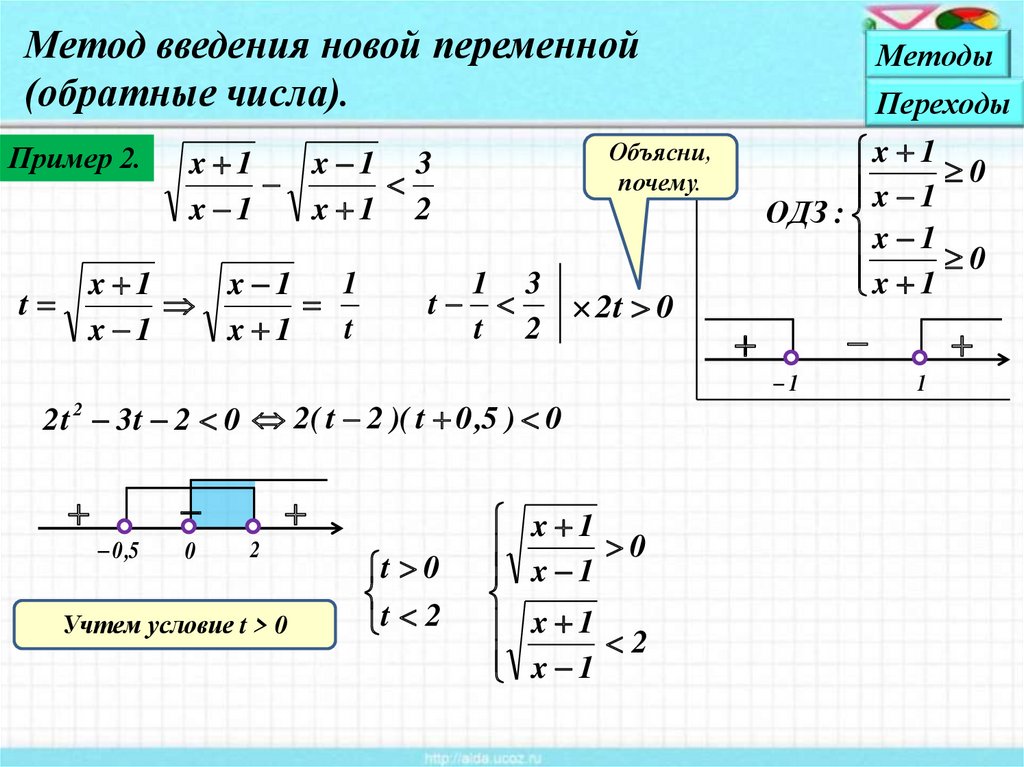
Метод введения новой переменной(обратные числа).
Пример 2.
t
1
x 1
t
x 1
Переходы
x 1
x 1 0
ОДЗ :
x 1 0
x 1
Объясни,
почему.
x 1
x 1 3
x 1
x 1 2
x 1
x 1
Методы
1 3
t
2t 0
t 2
1
2 t 2 3 t 2 0 2( t 2 )( t 0 ,5 ) 0
0 ,5
0
2
Учтем условие t > 0
t 0
t 2
x 1
0
x 1
x 1
2
x 1
1
21.
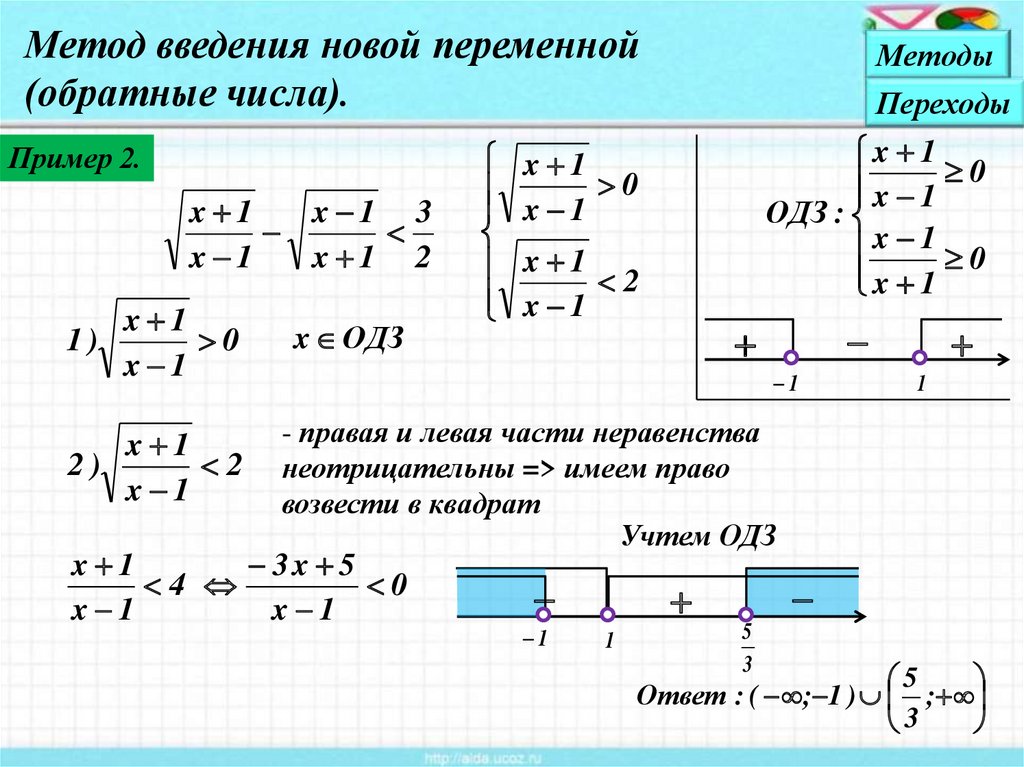
Метод введения новой переменной(обратные числа).
Пример 2.
x 1
x 1 3
x 1
x 1 2
1)
x 1
0
x 1
x 1
2)
2
x 1
x ОДЗ
Методы
Переходы
x 1
x 1 0
ОДЗ :
x 1 0
x 1
x 1
0
x 1
x 1
2
x 1
1
1
- правая и левая части неравенства
неотрицательны => имеем право
возвести в квадрат
Учтем ОДЗ
x 1
3x 5
4
0
x 1
x 1
1
1
5
3
5
Ответ : ( ; 1 ) ;
3
22.
Метод введения новой переменной.Методы
Переходы
Часто, даже если вы не видите повторяющиеся
и обратные выражения, введение новой переменной
может значительно облегчить решение неравенства.
2 x 3 0
ОДЗ :
x 2 0
3
x
2 x 2
x 2
2x 3 x 2 2
t x 2 t2 x 2 x t2 2
Пример 3.
2( t 2 ) 3 t 2
2
Объясни,
почему.
3
1
2t 2 7 2 t 2 t 2 7 ( 2 t )2 ( t 1 )( t 3 ) 0
Учтем ОДЗ
t 1
t 3
x 2 1
x 2 3
х 2 1 х 3
x 2 9 x 11
2
3
11
Ответ : [ 2 ;3 ) ( 11; )
23.
Метод введения новой переменной(полезна наблюдательность).
Методы
Переходы
Пример 4
x 2 3 2 x 2 3 x 2 1.5( x 4 ) ОДЗ : 2 x 2 3 x 2 0
D 0
a 0
2
2
2
x 3 2 x 3 x 2 1.5 x 6
x R
2 x 2 6 2 2 x 2 3 x 2 3 x 12
( 2 x2 3 x 2 ) 2 2 x2 3 x 2 8 0
t 2 2t 8 0
t 4
t 2
2
2 x2 3 x 2 4
2 x 2 3 x 2 2 Ø
t 2 x2 3 x 2
2 x2 3 x 2 t 2
Объясни,
почему.
4
2 x 2 3 x 2 4 2 x 2 3 x 2 16
2 x 2 3 x 14 0
2( x 2 )( x 3 ,5 ) 0
Ответ : ( ; 2 ] [ 3 ,5 ; )
2
3 ,5




















 mathematics
mathematics








