Similar presentations:
Показательная функция, ее свойства и график
1. Показательная функция, ее свойства и график.
2.
Рассмотрим функцию вида у = 2х,определенную на множестве всех
действительных чисел.
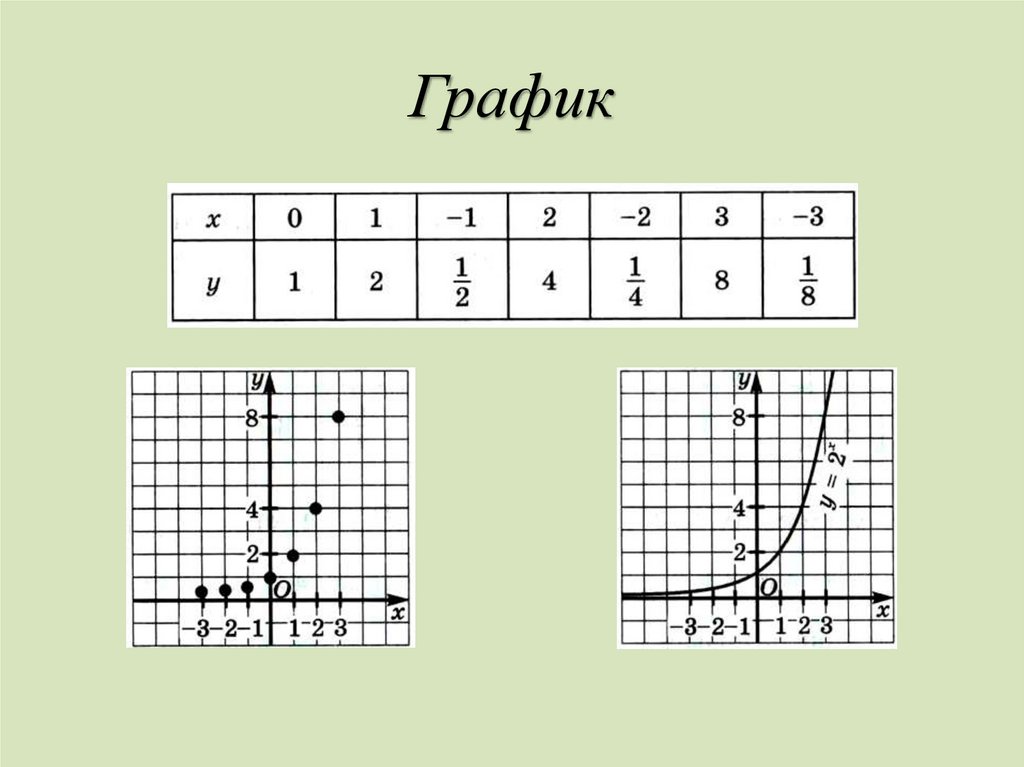
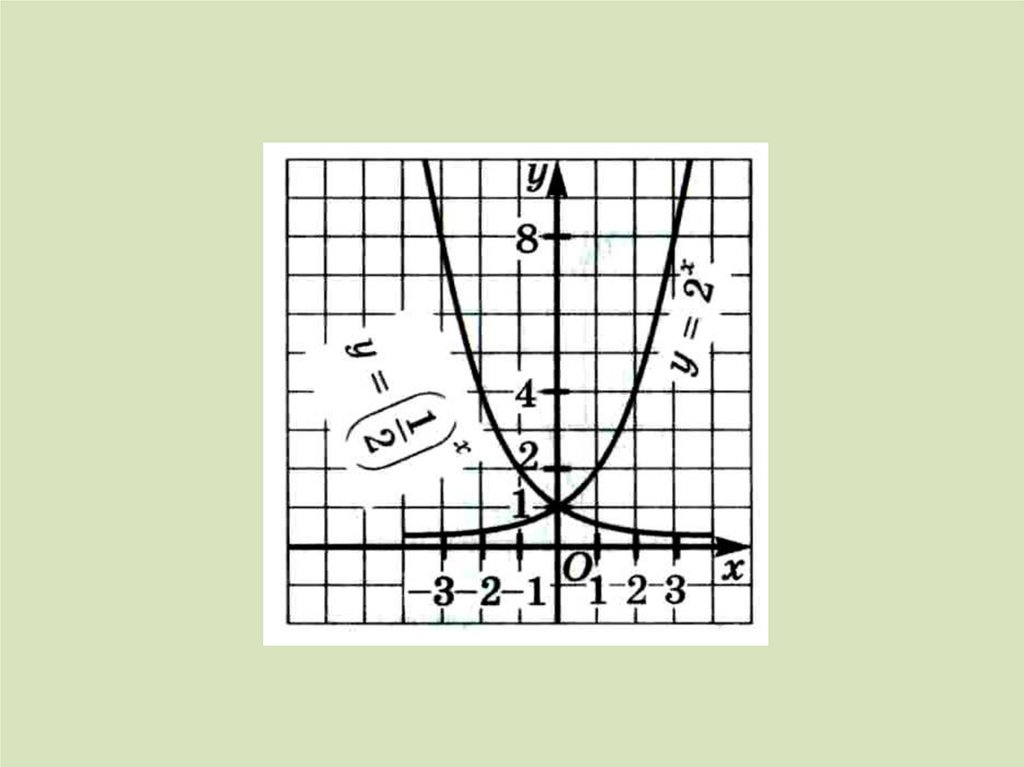
3. График
4. Свойства функции у = 2х
Свойства функции у =1.
2.
3.
4.
5.
6.
7.
8.
х
2
D(у): х (- ; + )
Функция общего вида
Возрастает
Ограничена снизу и не
ограничена сверху
Нет ни наибольшего, ни
наименьшего значений
Непрерывна
Е(у): у (0; + )
Выпукла вниз
5.
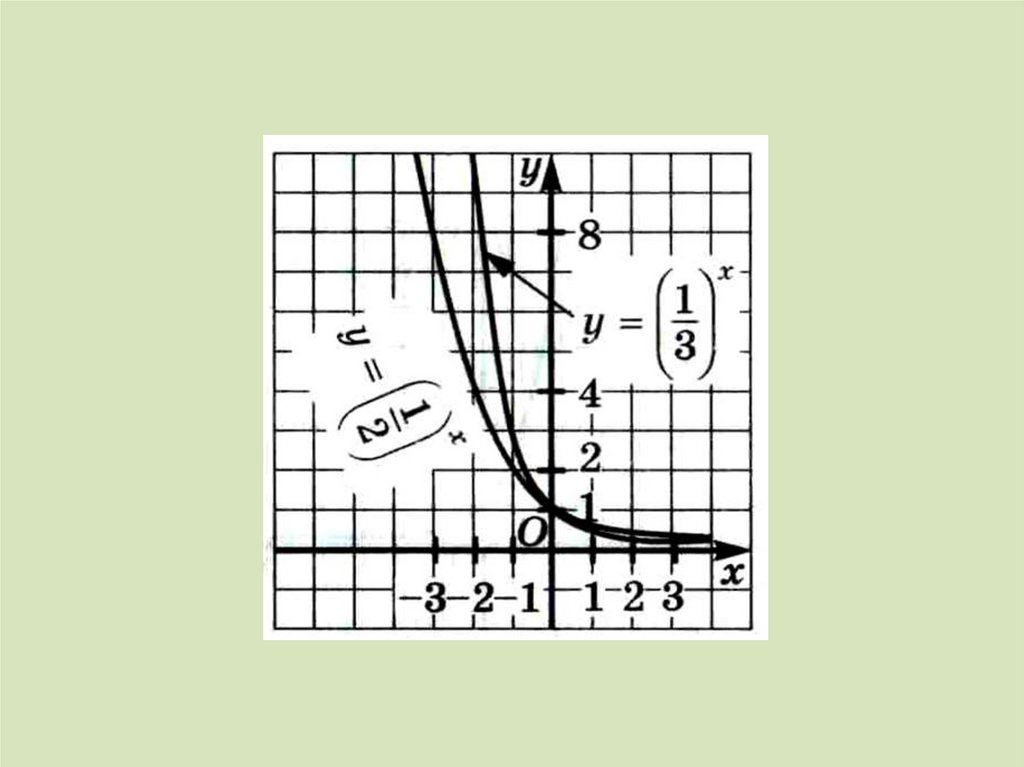
Точно такими же функциями обладаетлюбая функция вида у = ах , где а 1.
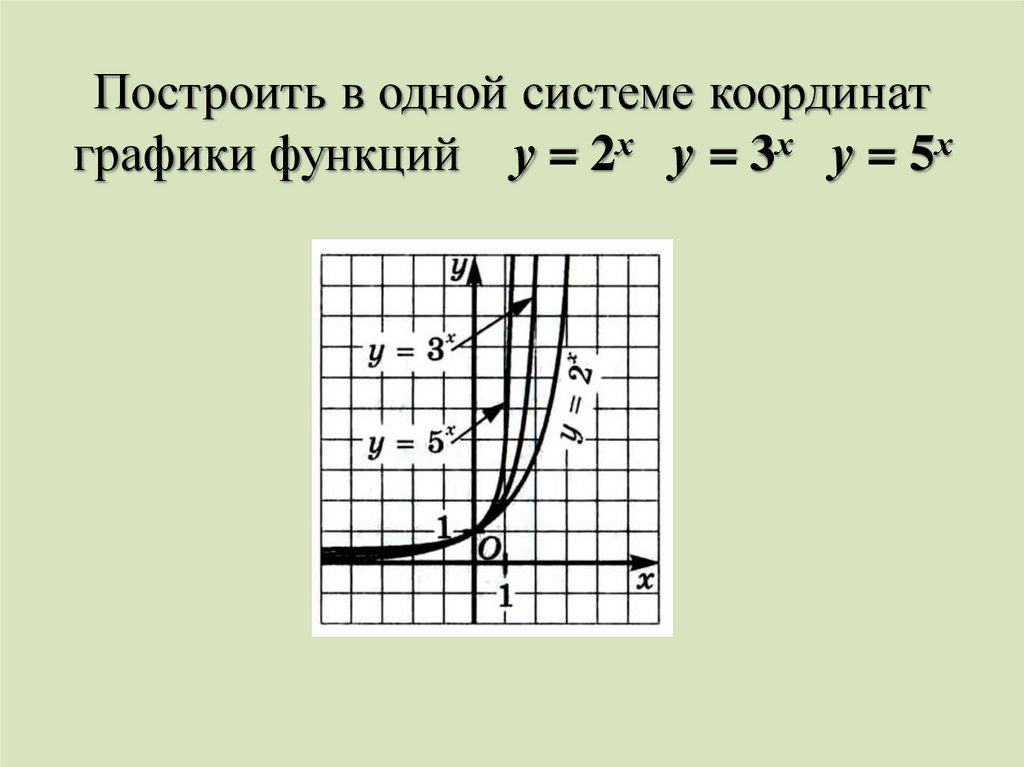
6. Построить в одной системе координат графики функций у = 2х у = 3х у = 5х
7.
у=х
8.
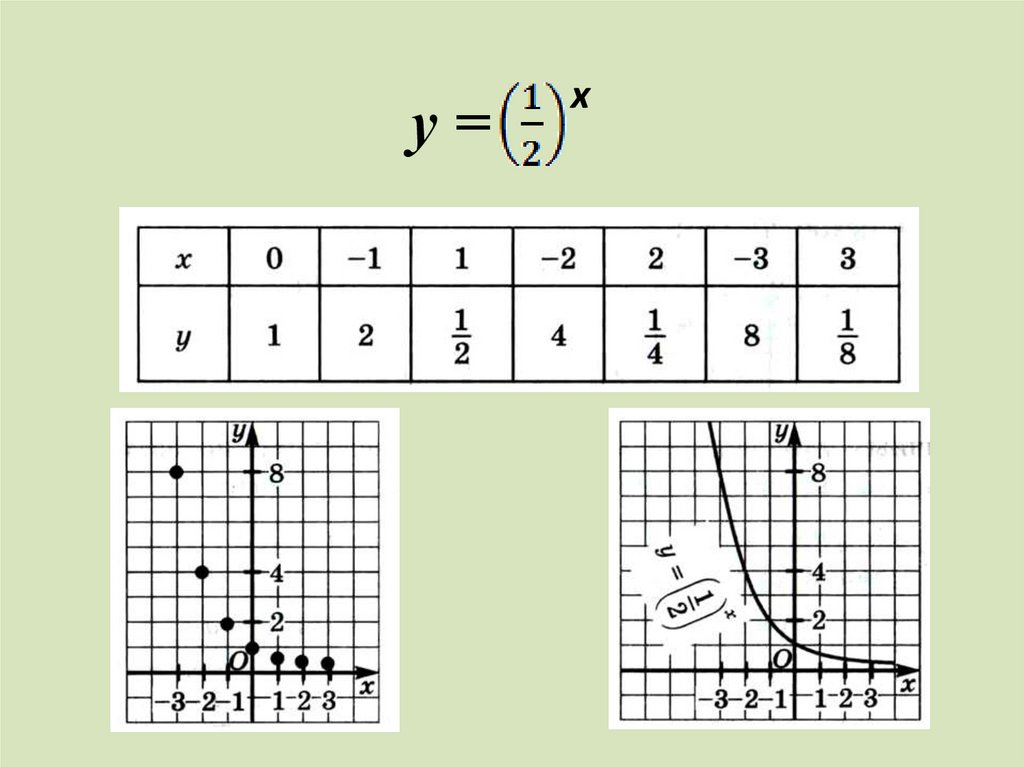
1.2.
3.
4.
5.
6.
7.
8.
D(у): х (- ; + )
Функция общего вида
Убывает
Ограничена снизу и
не ограничена сверху
Нет ни наибольшего,
ни наименьшего
значений
Непрерывна
Е(у): у (0; + )
Выпукла вниз
9.
10.
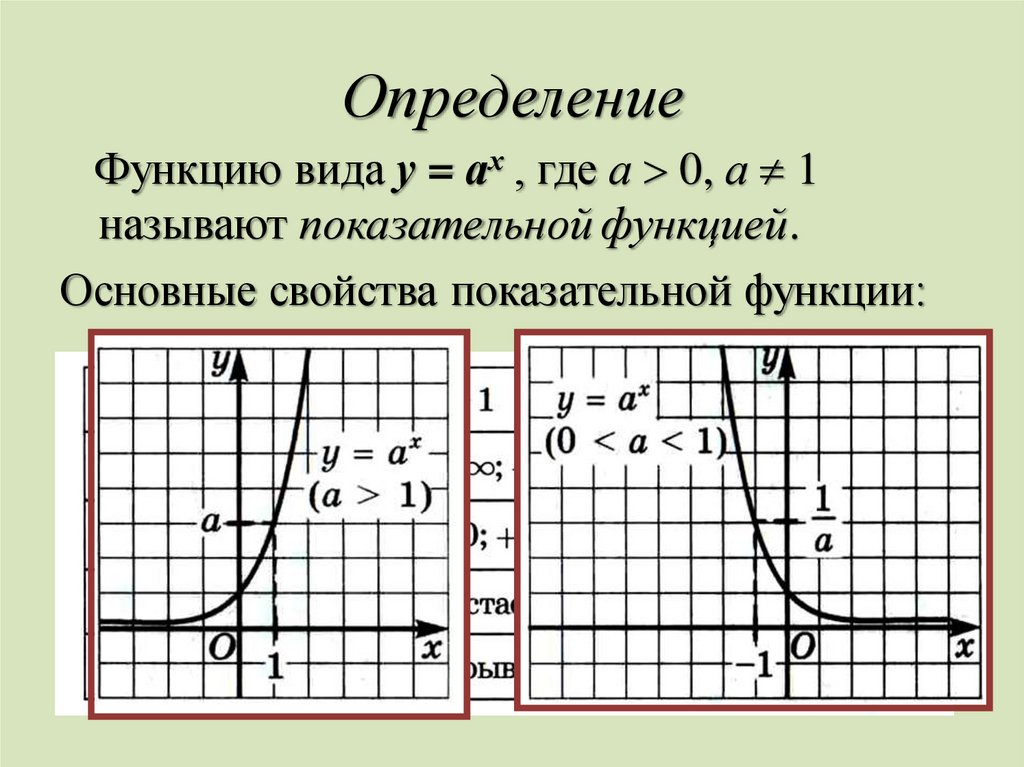
11. Определение
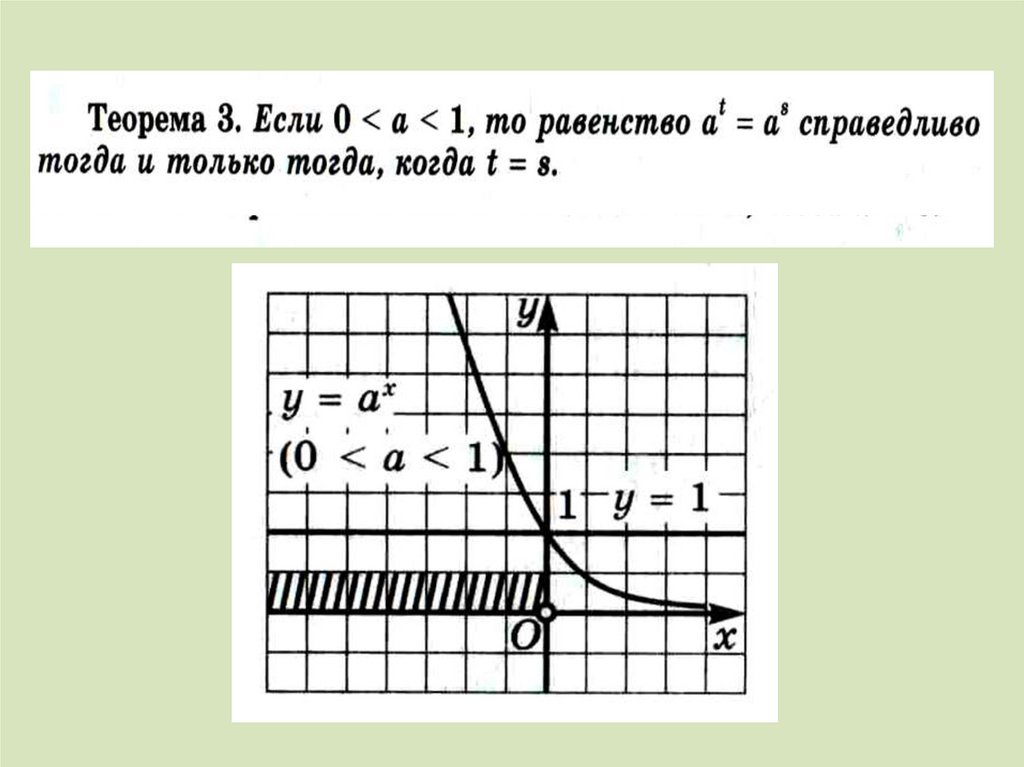
Функцию вида у = ах , где а 0, а 1называют показательной функцией.
Основные свойства показательной функции:
12.
13. Устная работа.
14.
15.
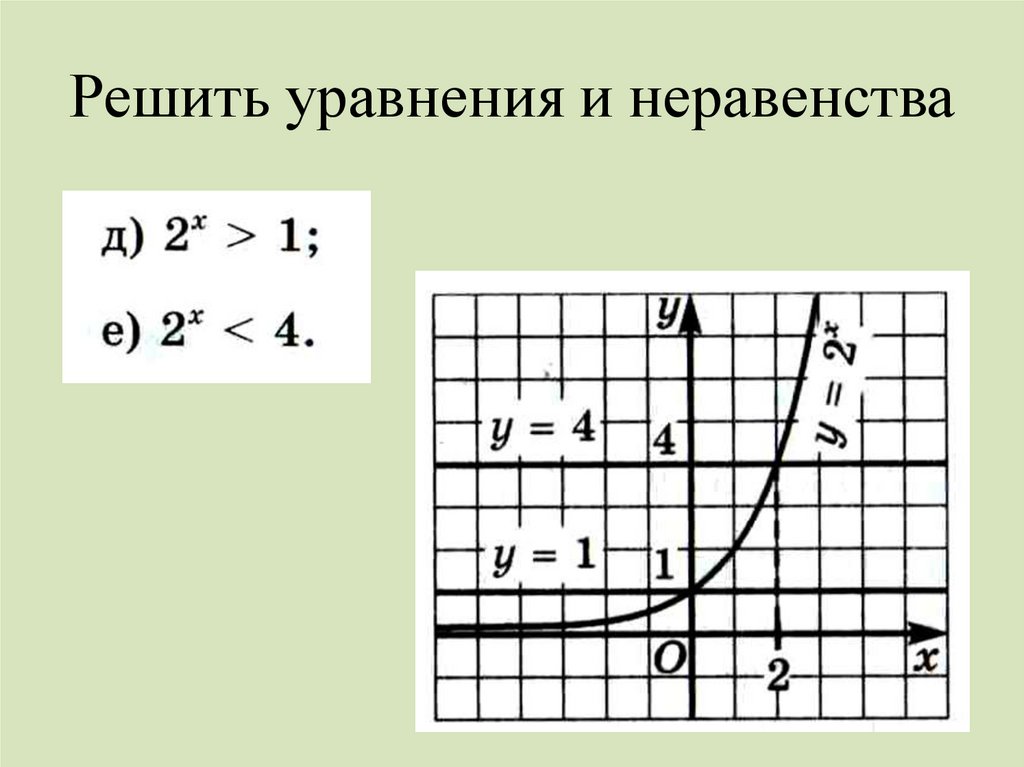
Устная работа.16. Решить уравнения и неравенства
17. Решить уравнения и неравенства
18.
19.
20. Примеры решения задач по теме
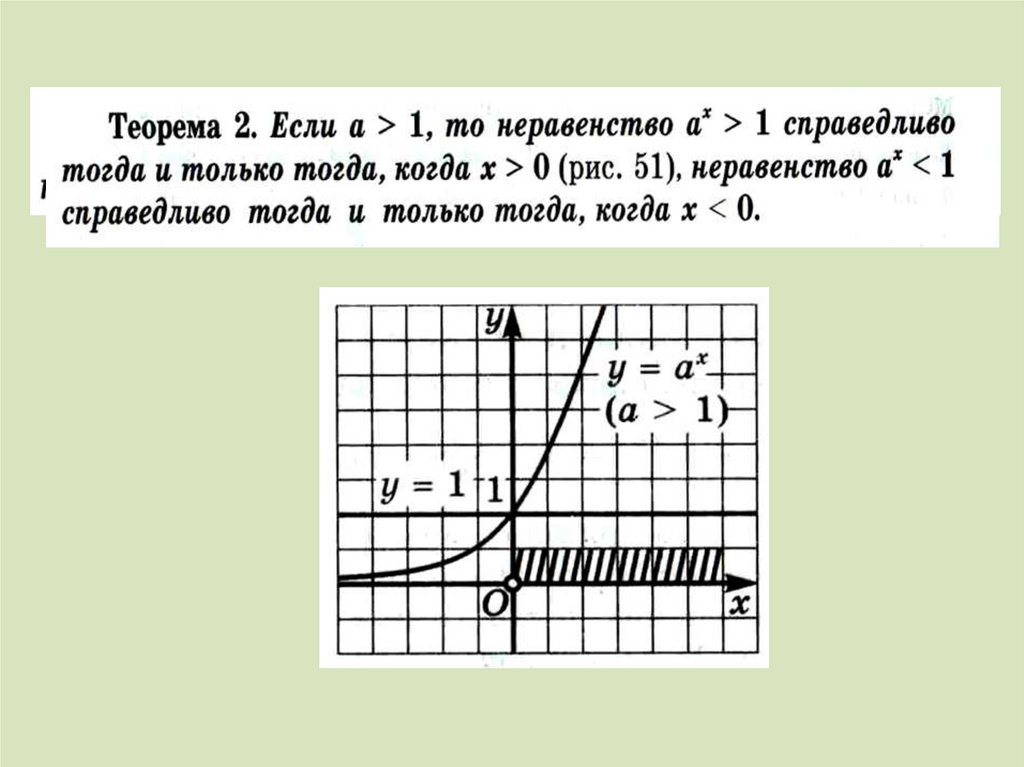
С помощью графиков функций (используясоответствующие свойства функций) можно
решать показательные уравнения и
неравенства, находить наибольшее и
наименьшее значения функции на отрезке.
21.
№ 1. Решите уравнение 23 x 1282
3x
2
7
воспользуемся тем, что
функция y = 2t монотонна
(возрастает), поэтому из равенства
следует
3x 7
1
x 2
3
22.
№ 2. Решите неравенство 8 x 648 x 82
так как функция y = 8t
возрастает при t ≥ 0, то x > 2.
23.
24.
Домашнее заданиеРешите уравнение:.
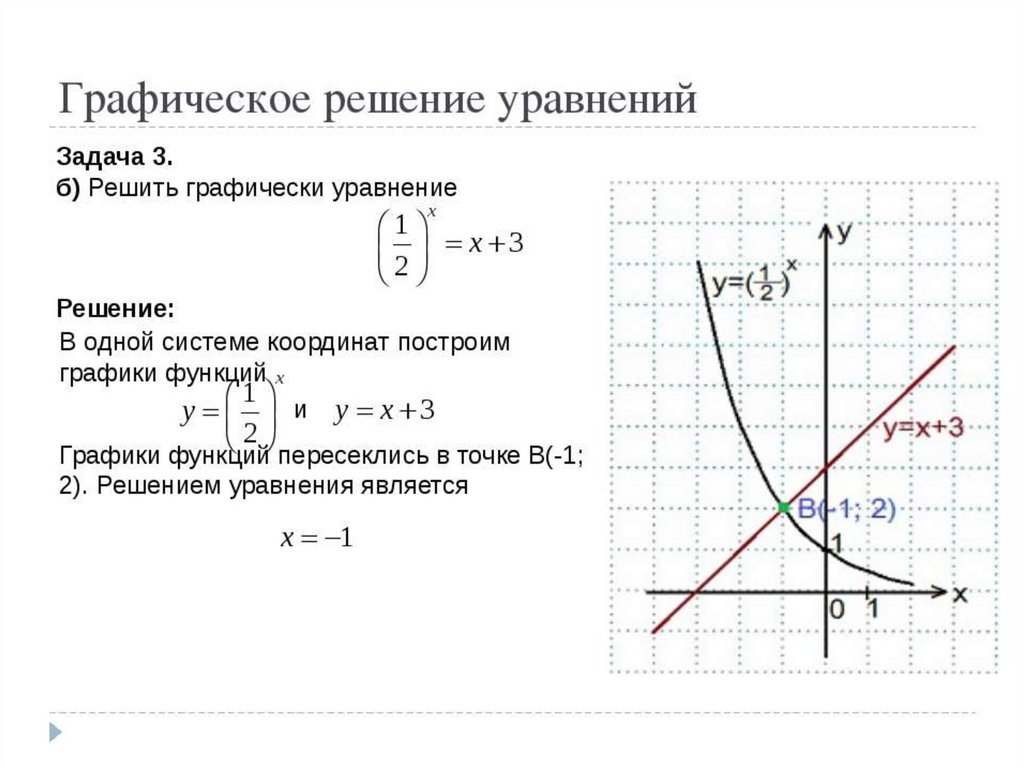
1) (0,2)x = x + 6
2) 3х= 4-х
3) 2х=х+2














 mathematics
mathematics








