Similar presentations:
Равномерное движение точки по окружности
1.
Движение материальнойточки по окружности
2.
Равномерное движениеточки по окружности.
3.
ТерминологияСкорость движения тела по окружности
носит название линейная скорость.
4.
Линейная скорость направлена покасательной к траектории и совпадает с
направлением движения.
5.
Время, за которое траектория точки опишетокружность, называется периодом
обращения точки (Т).
Т с
Число оборотов точки
за единицу времени
называется частотой
обращения (ν).
1
1
с
с
T
1
6.
Равномерное движение по окружности – этопростейший пример криволинейного движения.
Траектория движения точки (тела)- окружность.
1
1
2
2
R
r
3
2 R
2 r
1
2
T
T
1 2
1 3 1 3
При равномерном движении
тела по окружности модуль
скорости
тела
с
течением
времени не изменяется, то есть
υ = const, а изменяется только
направление вектора скорости .
7.
Центростремительное(нормальное) ускорение.
8.
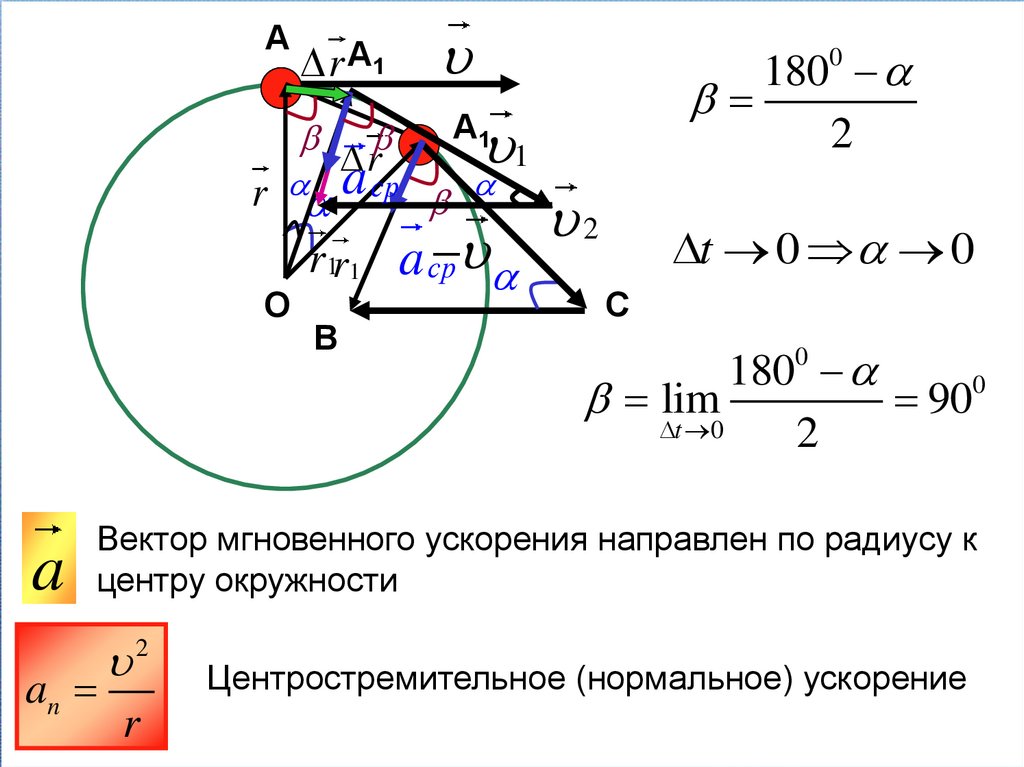
АО
AA1 r
А1
r
r
За Δt:
a ср
r1
В
AOA1
1
С
ACB
1
r
r
1
r
lim
lim
t 0 t r t 0 t
1
1
a
r
1
Центростремительное
(нормальное) ускорение —
ускорение точки,
характеризующее быстроту
изменения направления вектора
скорости.
a
2
r
9.
St
Скорость при равномерном
прямолинейном движении
За один полный оборот S=2πR, t=Т.
2 R
T
S
t
(2 R)
aц
2
T R
2
4 R
aц
2
T
2
aц 4 R
2 2
aц
T
2
R
1
10.
Аr А1
r
1
А1
r a ср
r1r1 a ср
О
a
В
180
2
0
2
t 0 0
С
1800
lim
900
t 0
2
Вектор мгновенного ускорения направлен по радиусу к
центру окружности
an
2
r
Центростремительное (нормальное) ускорение
11.
Тангенциальное(касательное),
центростремительное
(нормальное) и полное
ускорения.
12.
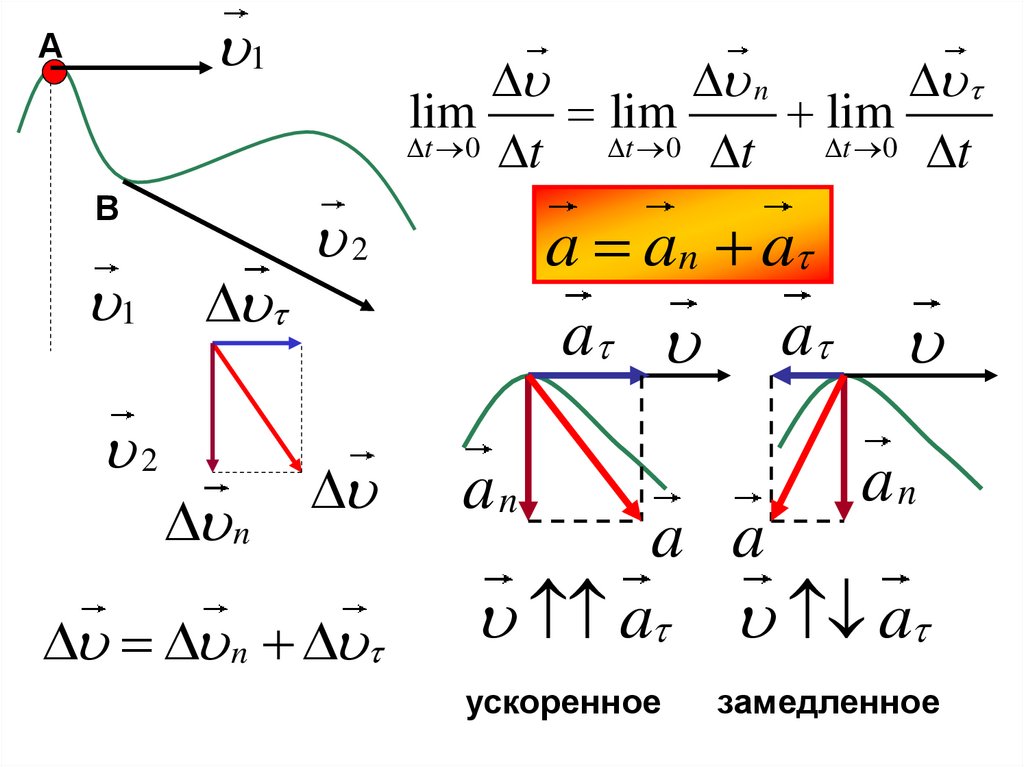
Если тело движется по окружности неравномерно,то появляется касательная (тангенциальная)
составляющая ускорения.
Касательное (тангенциальное) ускорение
характеризует быстроту изменения модуля
вектора скорости.
Полное ускорение равно векторной сумме
нормального и тангенциального ускорений.
13.
1А
В
1
2
n
n
lim
lim
lim
t 0 t
t 0 t
t 0 t
2
n
a an a
a a
an
an
a a
a a
ускоренное
замедленное
14.
Угловая скорость и угловоеускорение.
15.
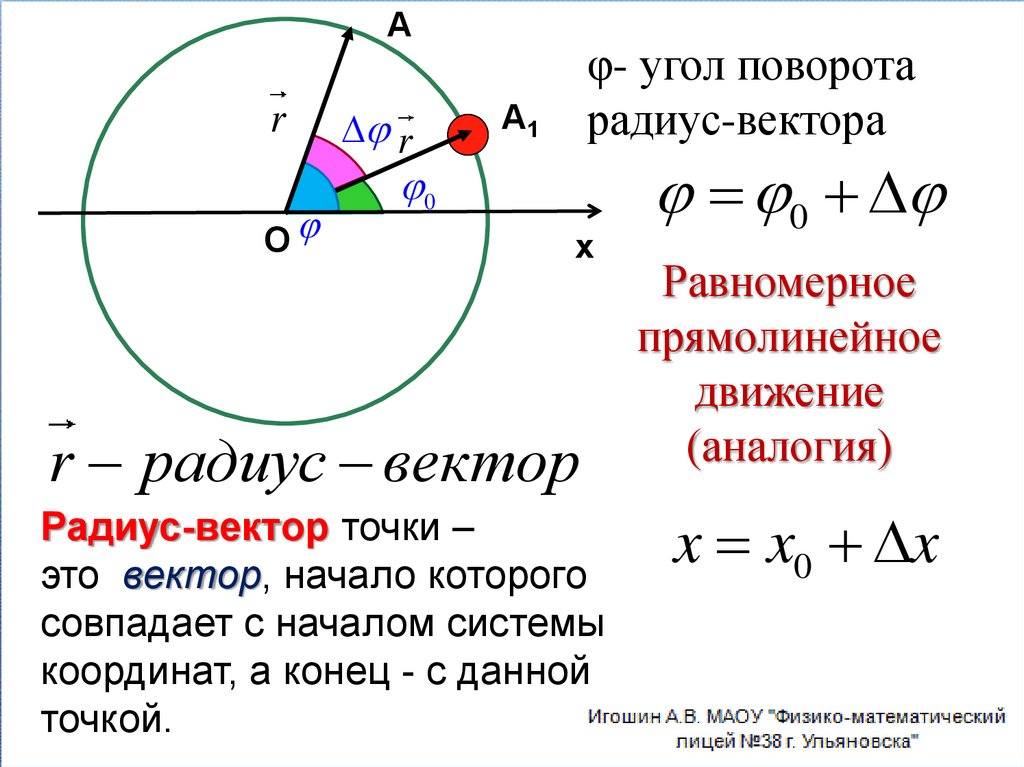
Аr
О
r
φ- угол поворота
радиус-вектора
А1
0
x
r радиус вектор
Радиус-вектор точки –
это вектор, начало которого
совпадает с началом системы
координат, а конец - с данной
точкой.
0
Равномерное
прямолинейное
движение
(аналогия)
x x0 x
16.
Угловая скорость характеризует быстротуизменения угла поворота.
Угловой скоростью при равномерном
движении по окружности называется отношение
угла поворота Δφ радиус-вектора к промежутку
времени Δt, за который этот оборот произошел.
t
рад
с
За один полный оборот Δφ=2π, Δt=Т.
2
Т
17.
tt t t0
если t0 0 то t t
t
0
Равномерное
прямолинейное
движение
(аналогия)
0 t
x x0 xt
18.
Угловое ускорение величина, характеризующаябыстроту изменения угловой скорости точки.
Угловым ускорением при равнопеременном
движении по окружности называется отношение
изменения угловой скорости Δω к промежутку
времени Δt, за которое это изменение произошло.
t
x
ax
t
рад
2
с
Равнопеременное
прямолинейное движение
(аналогия)
19.
0t
0 t
Скорость при равнопеременном
движении по окружности
ускоренное
замедленное
Равнопеременное
прямолинейное
движение
(аналогия)
x 0 x axt
20.
t2
Уравнение
равнопеременного
движения точки по
окружности
ax t
x x0 0 xt
2
Равнопеременное
прямолинейное
движение
(аналогия)
0 0t
2
ускоренное
замедленное
2
21.
Связь между линейными иугловыми величинами.
22.
АS
r
r
А1
О
Δφ- центральный угол
S R
x
S R
t t
R
aц
aц
2
R
R
R
2
R
2
aц R
2
23.
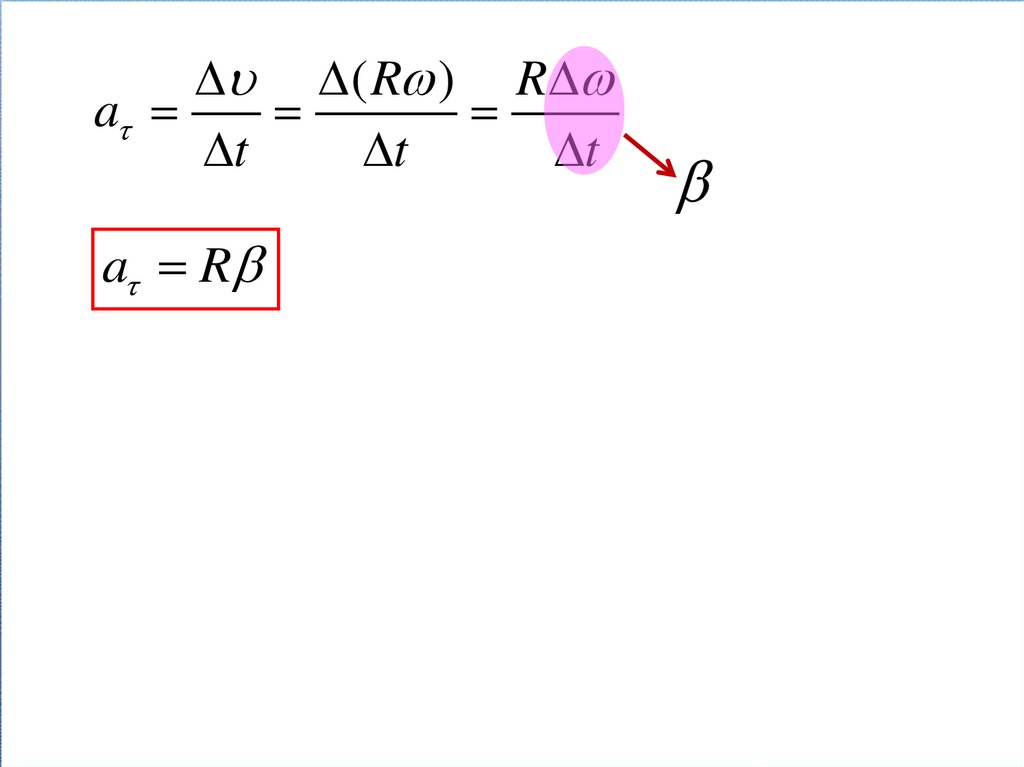
( R ) Ra
t
t
t
a R



















 physics
physics








