Логарифмическая функция

1.

x - независимая переменная, аргумент
y - зависимая переменная, функция

2.

Если функция y f (x) - обратимая, то
она является обратной.
Достаточное условие существования
обратимой функции к данной функции
и есть ее монотонность, т.е.
возрастание и убывание на всей
области определения.

3.

Если
f
и
g
- функции, и они обратные друг другу, то необходимы следующие
условия:
f
область определения функции
т.е.
D f E g ,
совпадает с областью значений функции
и наоборот область значения функции
g , т.е. E f D g .
то и функция g возрастает;
f
g,
совпадает с
областью определения функции
если функция
f
возрастает,
убывает, то и функция
g
f
убывает;
графики данной функции
относительно прямой
если функция
y x.
f
и обратной функции
g,
симметричны

4.

a 1
0 a 1

5.

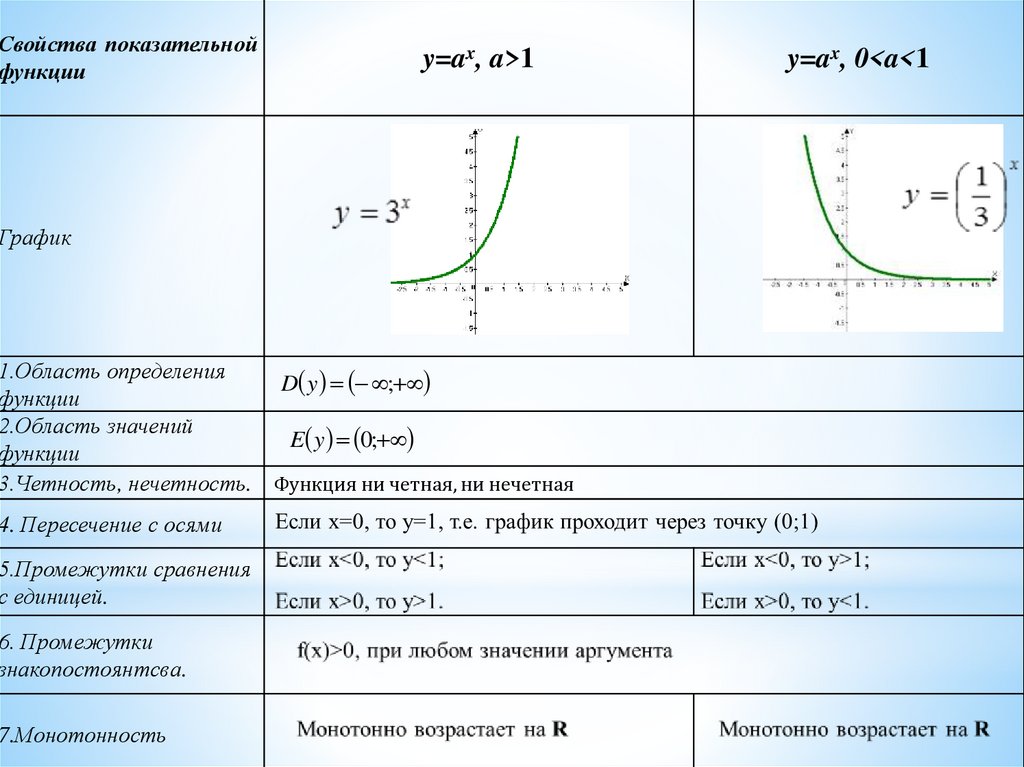
Свойства показательной
функции
y=ax, a>1
График
1.Область определения
D y ;
функции
2.Область значений
E y 0;
функции
3.Четность, нечетность. Функция ни четная, ни нечетная
4. Пересечение с осями
5.Промежутки сравнения
с единицей.
6. Промежутки
знакопостоянтсва.
7.Монотонность
y=ax, 0<a<1

6.

y log a x ,
a 0, a 1 ,
Функция
где
называется логарифмической функцией,
которая
является
обратной
к
показательной функции y a .
x

7.

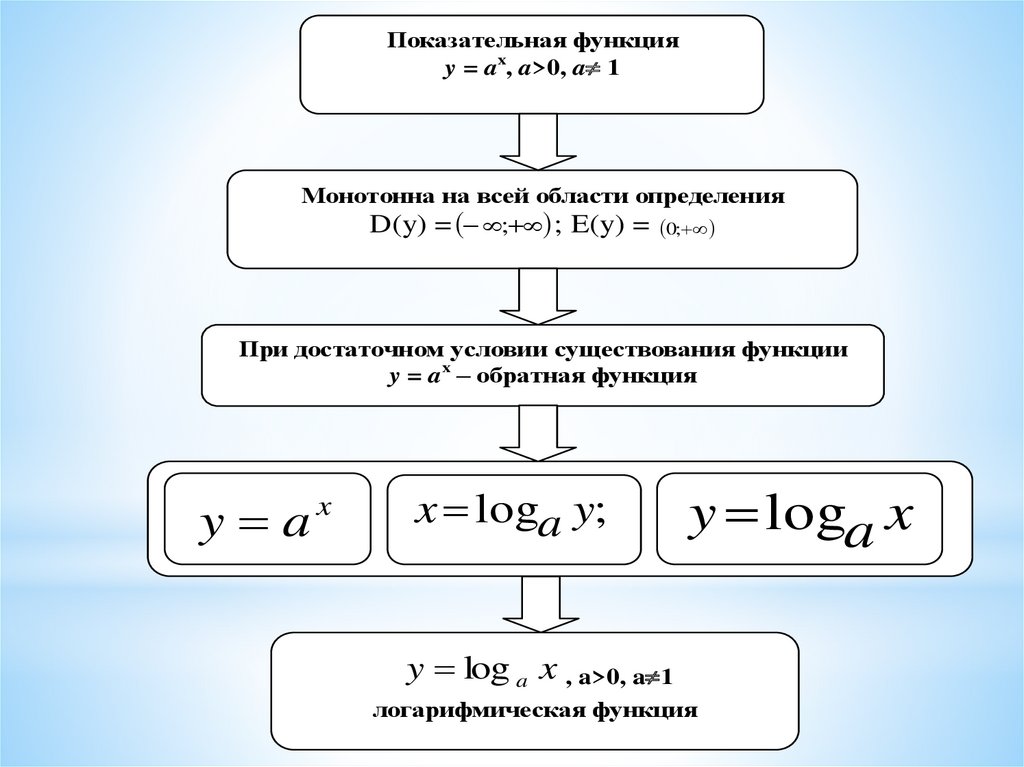
Показательная функция
y = ax, a>0, a 1
Монотонна на всей области определения
D(y) = ; ; E(y) = 0;
При достаточном условии существования функции
y = ax – обратная функция
y a
x
x loga y;
y loga x
y log a x , a>0, a 1
логарифмическая функция

8.

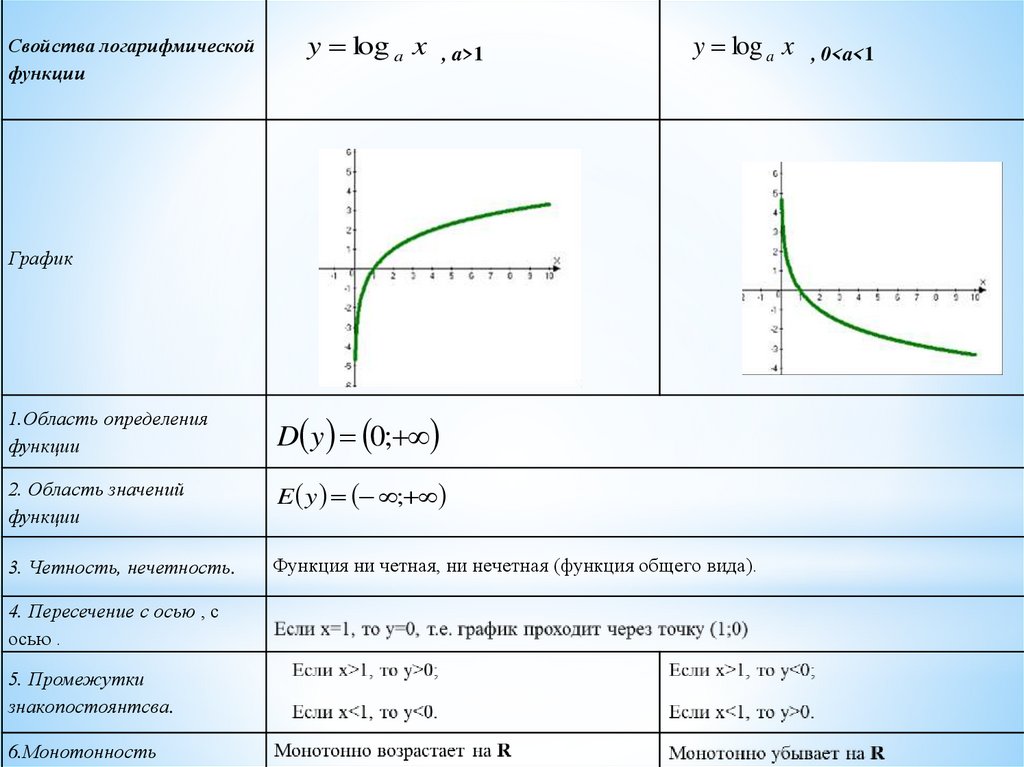
Свойства логарифмической
функции
y log a x
, a>1
y log a x
График
1.Область определения
функции
D y 0;
2. Область значений
функции
E y ;
3. Четность, нечетность.
Функция ни четная, ни нечетная (функция общего вида).
4. Пересечение с осью , с
осью .
5. Промежутки
знакопостоянтсва.
6.Монотонность
, 0<a<1

9.

Какой вывод можно сделать
относительно этих логарифмов?
log 5 4 log 5 2;
log 2 5 log 2 3;
log 4 6 log 4 4.
log 1 5 log 1 3;
2
2
log 1 6 log 1 4;
3
3
log 1 7 log 1 5.
4
4

10.

Сделайте вывод в общем виде, когда при основании
a 1, log a N1 log a N 2 и 0 a 1, log a N1 log a N 2 ?
Вывод:
Логарифм чисел при основании a 1 , если N1 N 2 , то и
log a N1 log a N 2 , т.е. большее число имеет больший логарифм.
Логарифм чисел при основании 0 a 1 , если N1 N 2 , то
log a N1 log a N 2 , т.е. большее число имеет меньший логарифм.

11.

Определить знак неравенства,
используя свойства логарифма.
1) log 2 2 и log 5 5 ;
2) log 2 1 и log 3 1
log 2 2 log 5 5 1 , т.к. любой log a a 1
log 2 1 log 3 1 0 , т.к. логарифм 1 при любом основании равен нулю.

12.

13.

Логарифмическая линейка

14.

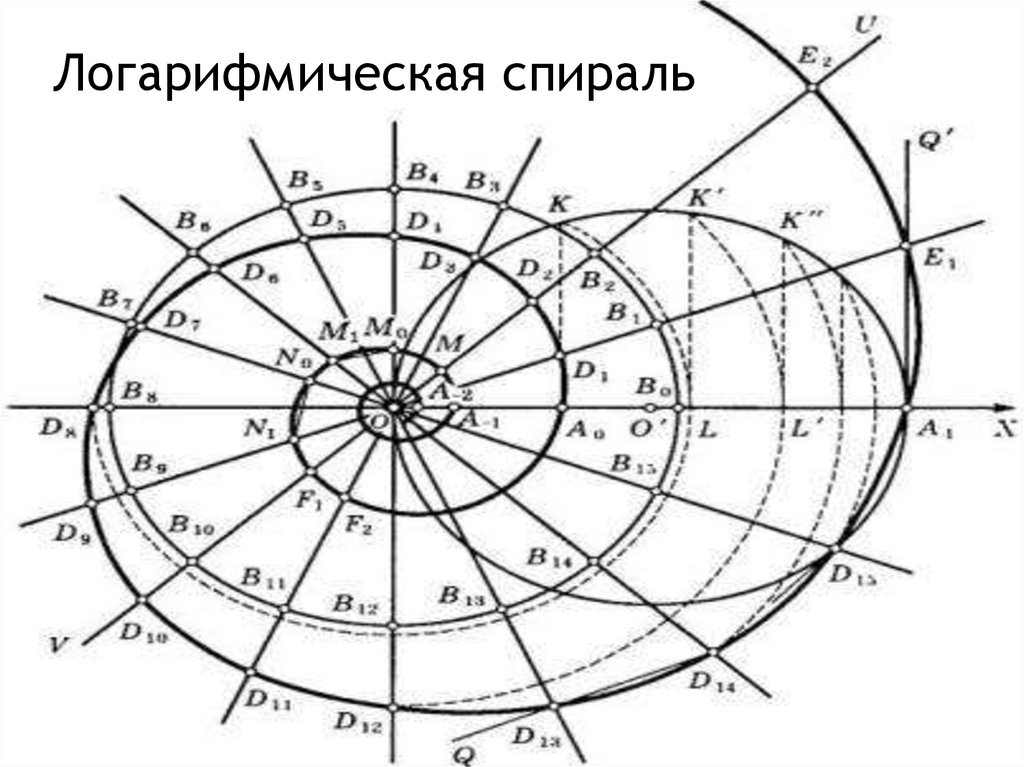
Логарифмическая спираль

15.

Логарифмическая спираль

16.

17.

Работа, которую выполняет газ
при изометрическом процессе:
V1 m
P1
A RT ln
RT
V2
P2
m
Ёмкость цилиндрического
конденсатора:
2l 0
С
R
ln
r

18.

19.

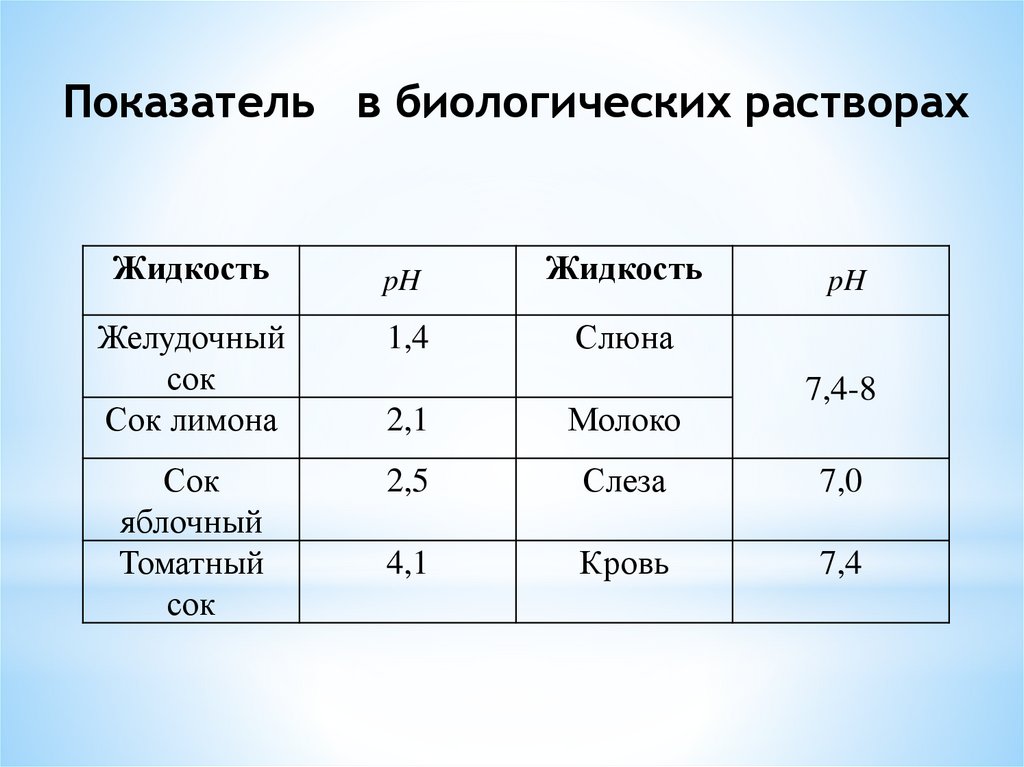
Показатель в биологических растворах
Жидкость
pH
Жидкость
Желудочный
сок
Сок лимона
1,4
Слюна
2,1
Молоко
Сок
яблочный
Томатный
сок
2,5
Слеза
7,0
4,1
Кровь
7,4
pH
7,4-8