Построение сбалансированного дерева поиска

1. ПОСТРОЕНИЕ СБАЛАНСИРОВАННОГО ДЕРЕВА ПОИСКА

Идеальное сбалансированное дерево поиска – это
двоичное дерево, в котором число вершин в левых
и правых поддеревьях отличается не более чем на 1.
Сбалансированное дерево поиска – это двоичное
дерево, в котором высоты левых и правых
поддеревьев каждой из его вершин отличаются не
более чем на 1.

2.

АЛГОРИТМ ПОСТРОЕНИЯ
СБАЛАНСИРОВАННОГО ДЕРЕВА ПОИСКА
При добавлении узла считаем баланс его «отца» (p) и
«деда» (gp) и всех остальных «предков»
Баланс узла определяется как разность высот его
правого и левого поддерева:
h=R–L
Если для какого-то узла (u) h(gp) = 2 или –2 то делаем
однократный или двукратный поворот.

3.

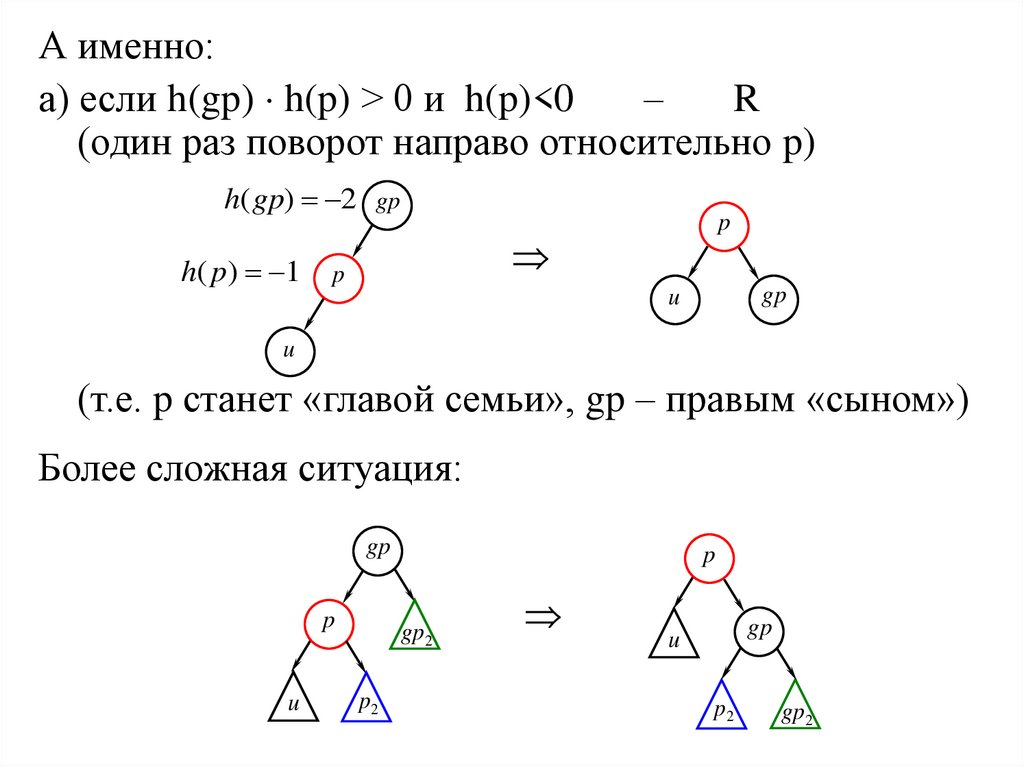
А именно:
а) если h(gp) h(p) > 0 и h(p)<0
–
R
(один раз поворот направо относительно p)
h( gp) 2
h( p) 1
gp
p
p
gp
u
u
(т.е. p станет «главой семьи», gp – правым «сыном»)
Более сложная ситуация:
gp
p
u
p
gp 2
p2
gp
u
p2
gp 2

4.

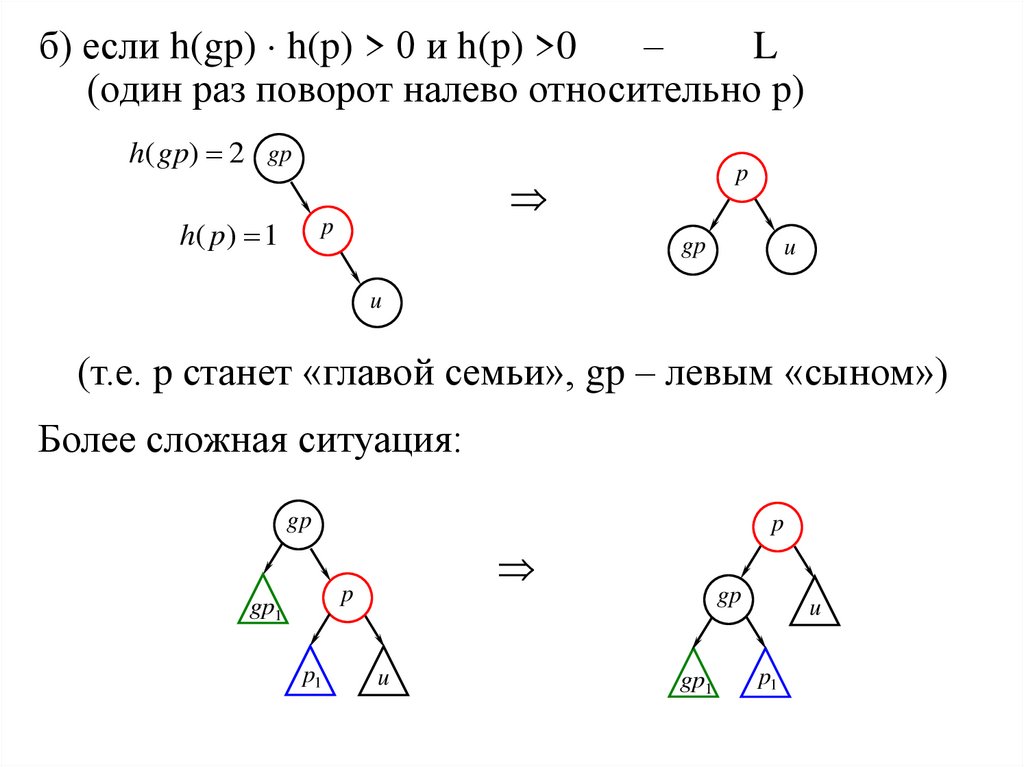
б) если h(gp) h(p) > 0 и h(p) >0
–
L
(один раз поворот налево относительно p)
h( gp) 2
gp
h( p ) 1
p
p
gp
u
u
(т.е. p станет «главой семьи», gp – левым «сыном»)
Более сложная ситуация:
gp
p
p
gp1
p1
u
gp
gp1
u
p1

5.

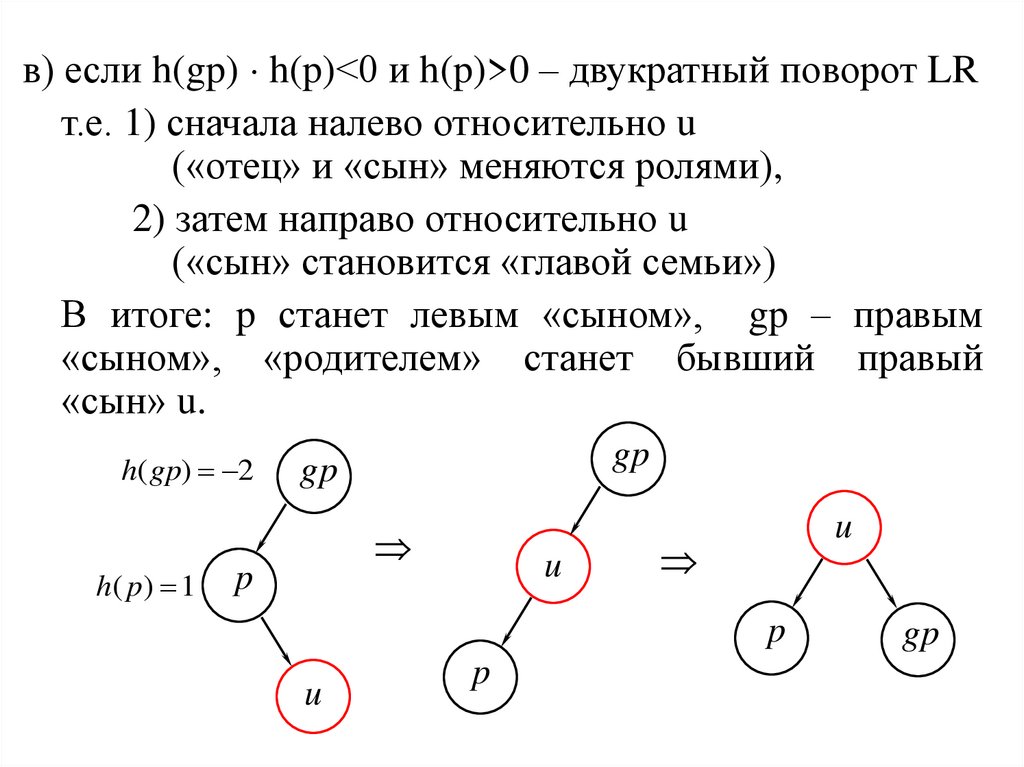
в) если h(gp) h(p)<0 и h(p)>0 – двукратный поворот LR
т.е. 1) сначала налево относительно u
(«отец» и «сын» меняются ролями),
2) затем направо относительно u
(«сын» становится «главой семьи»)
В итоге: p станет левым «сыном», gp – правым
«сыном», «родителем» станет бывший правый
«сын» u.
h( gp) 2
h( p ) 1
gp
gp
p
u
u
p
u
p
gp

6.

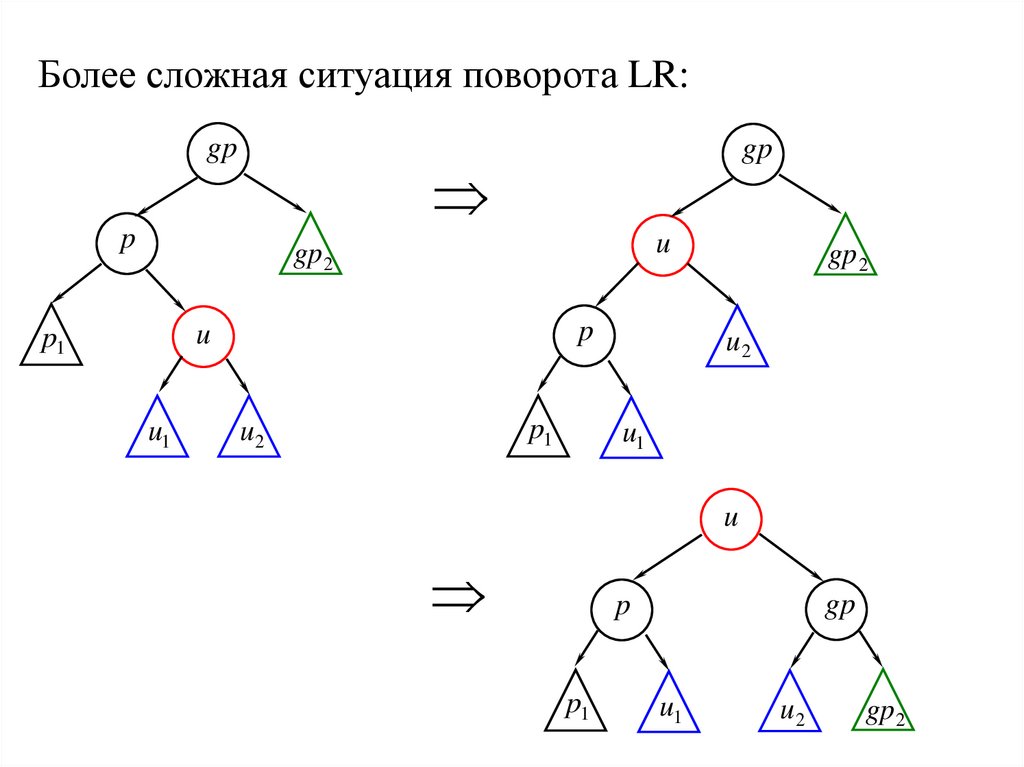
Более сложная ситуация поворота LR:
gp
gp
p
u
gp 2
p
u
p1
u1
p1
u2
gp 2
u2
u1
u
gp
p
p1
u1
u2
gp 2

7.

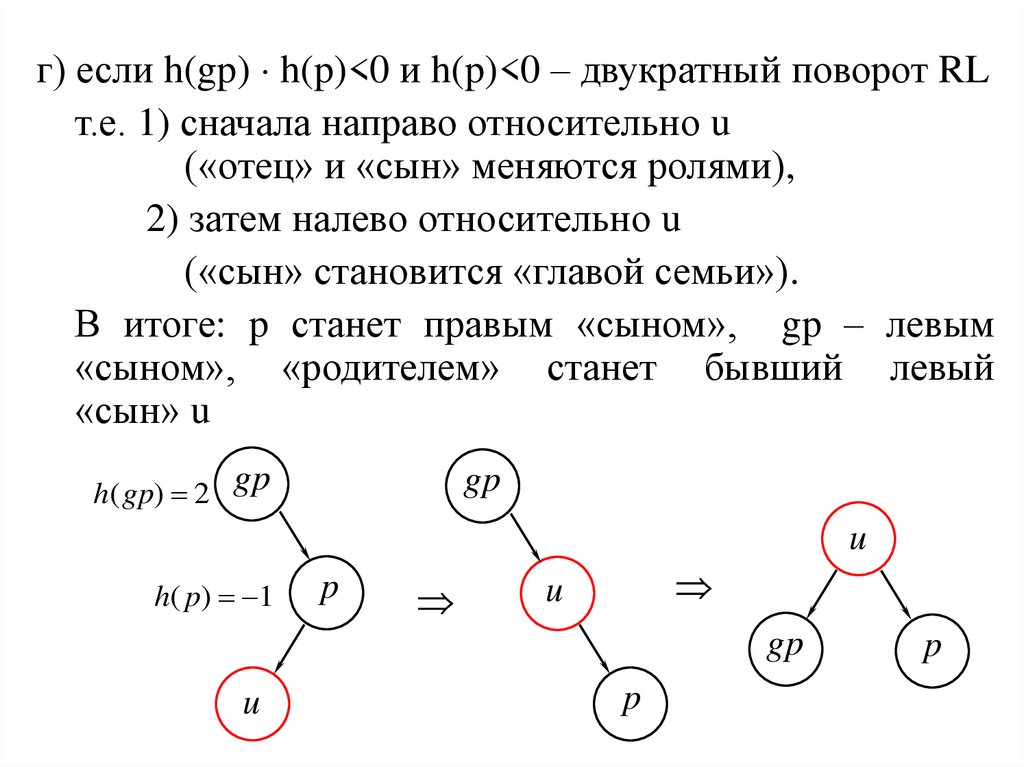
г) если h(gp) h(p)<0 и h(p)<0 – двукратный поворот RL
т.е. 1) сначала направо относительно u
(«отец» и «сын» меняются ролями),
2) затем налево относительно u
(«сын» становится «главой семьи»).
В итоге: p станет правым «сыном», gp – левым
«сыном», «родителем» станет бывший левый
«сын» u
h( gp) 2 gp
gp
u
h( p) 1
p
u
gp
u
p
p

8.

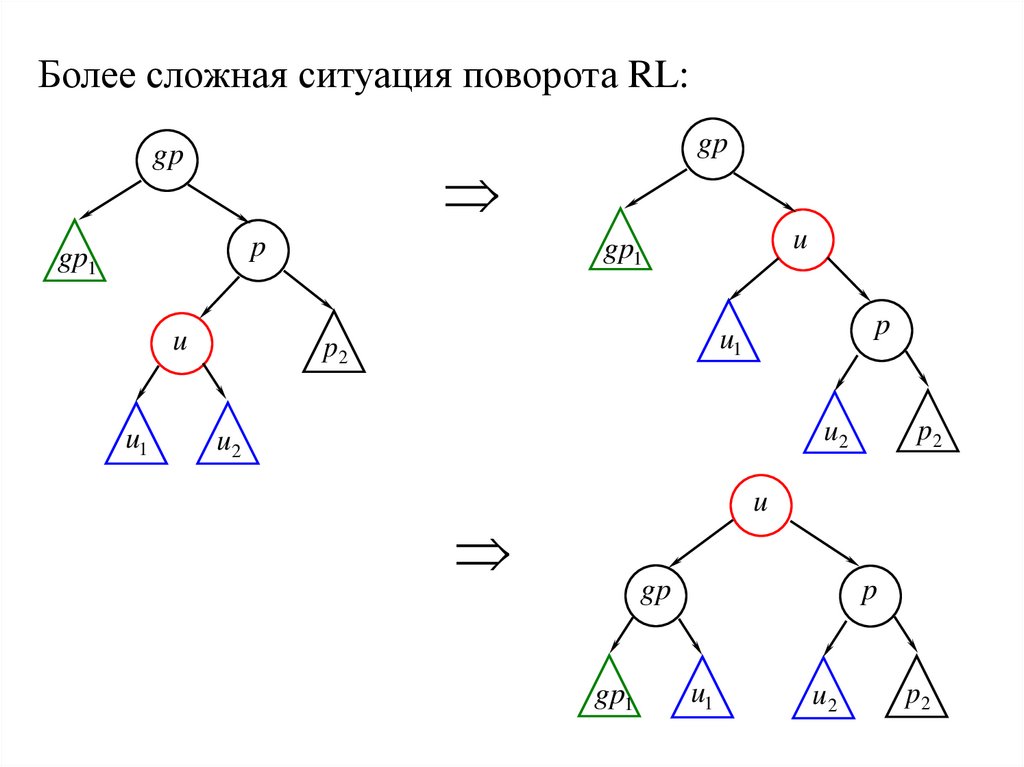
Более сложная ситуация поворота RL:
gp
p
gp1
u
u1
gp
u
gp1
p
u1
p2
p2
u2
u2
u
p
gp
gp1
u1
u2
p2

9.

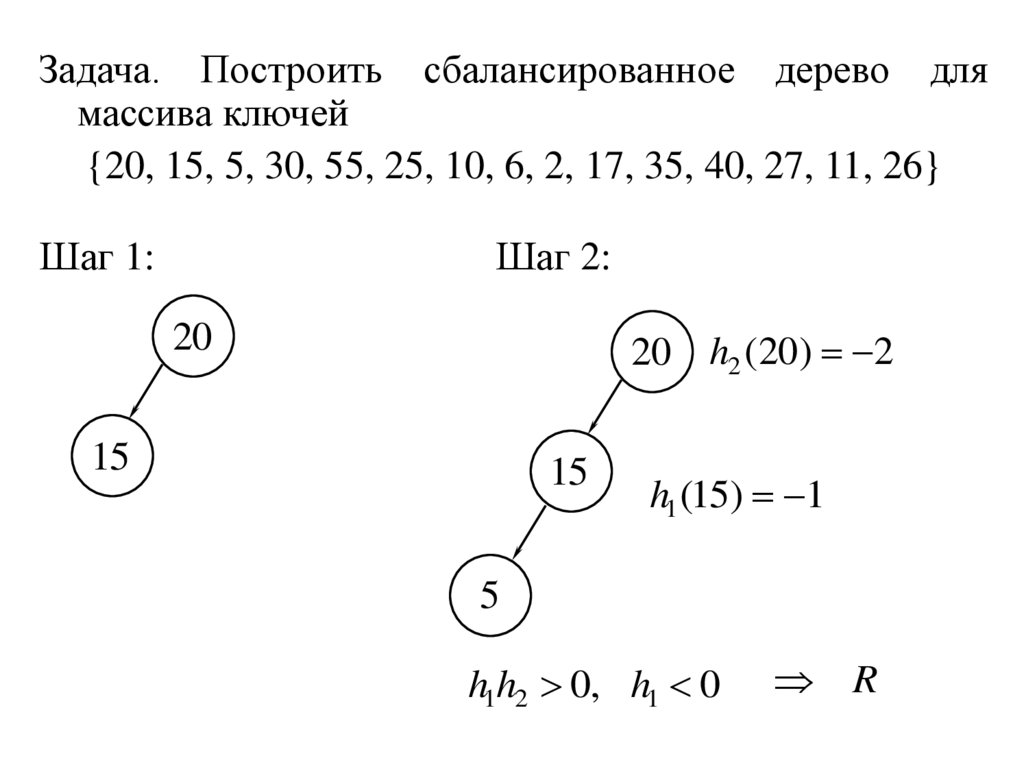
Задача. Построить сбалансированное дерево для
массива ключей
{20, 15, 5, 30, 55, 25, 10, 6, 2, 17, 35, 40, 27, 11, 26}
Шаг 1:
Шаг 2:
20
20 h2 (20) 2
15
15
h1 (15) 1
5
h1h2 0, h1 0
R

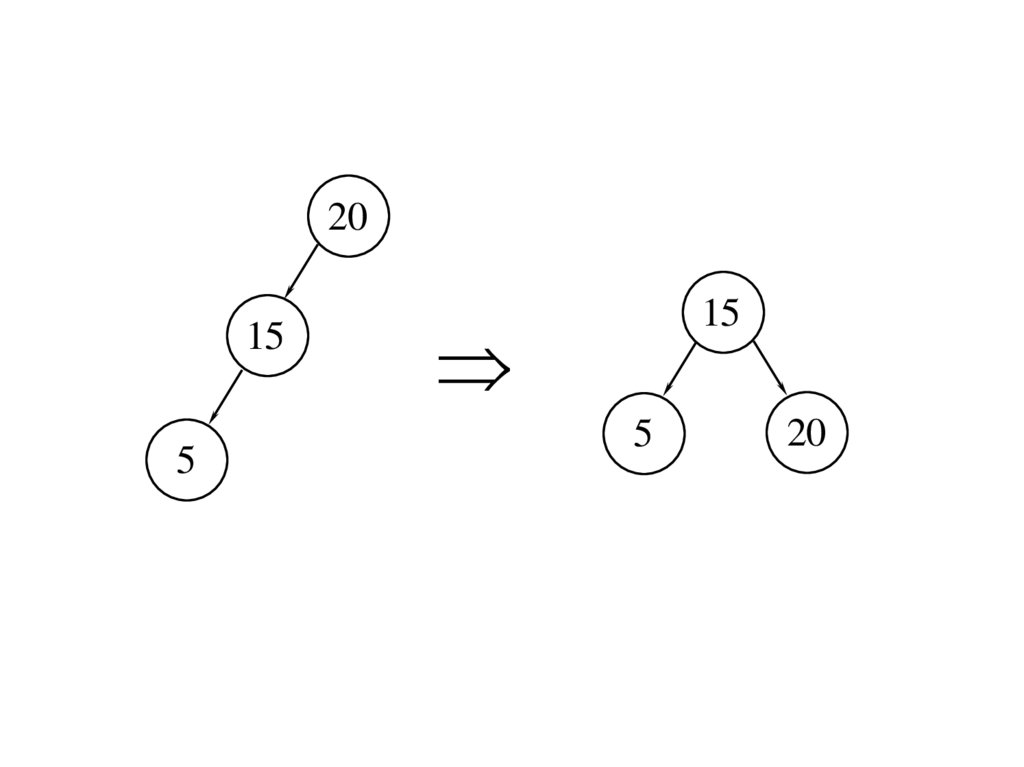
10.

20
15
5
15
5
20

11.

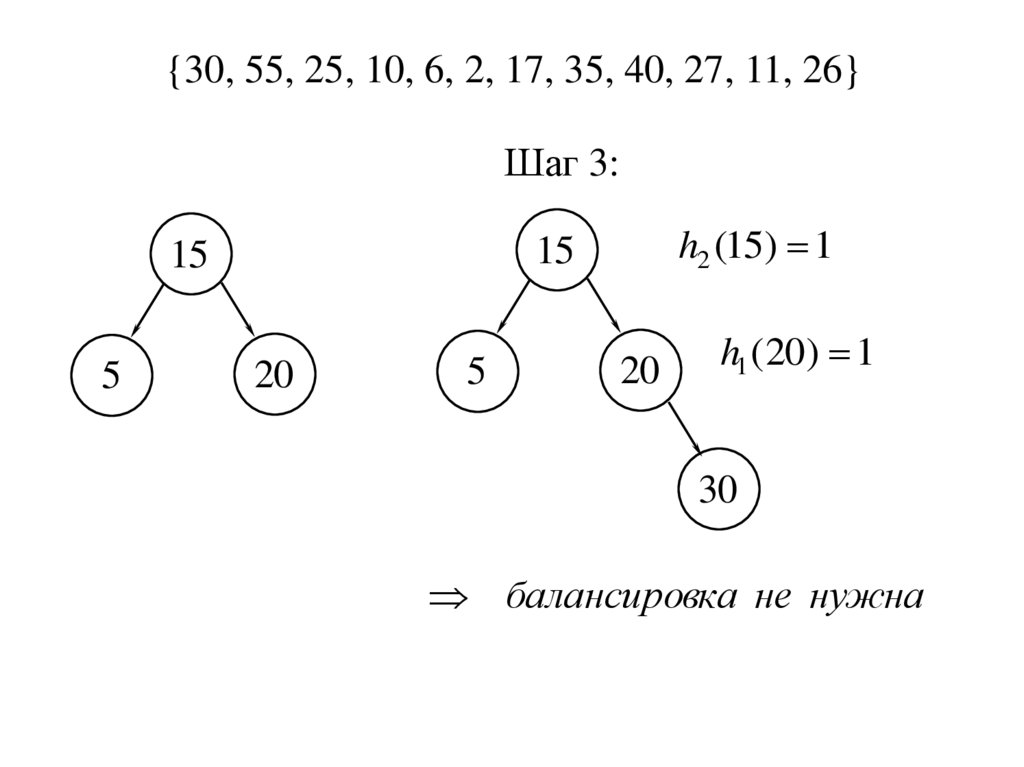
{30, 55, 25, 10, 6, 2, 17, 35, 40, 27, 11, 26}
Шаг 3:
5
h2 (15) 1
15
15
20
5
20
h1 (20) 1
30
балансировка не нужна

12.

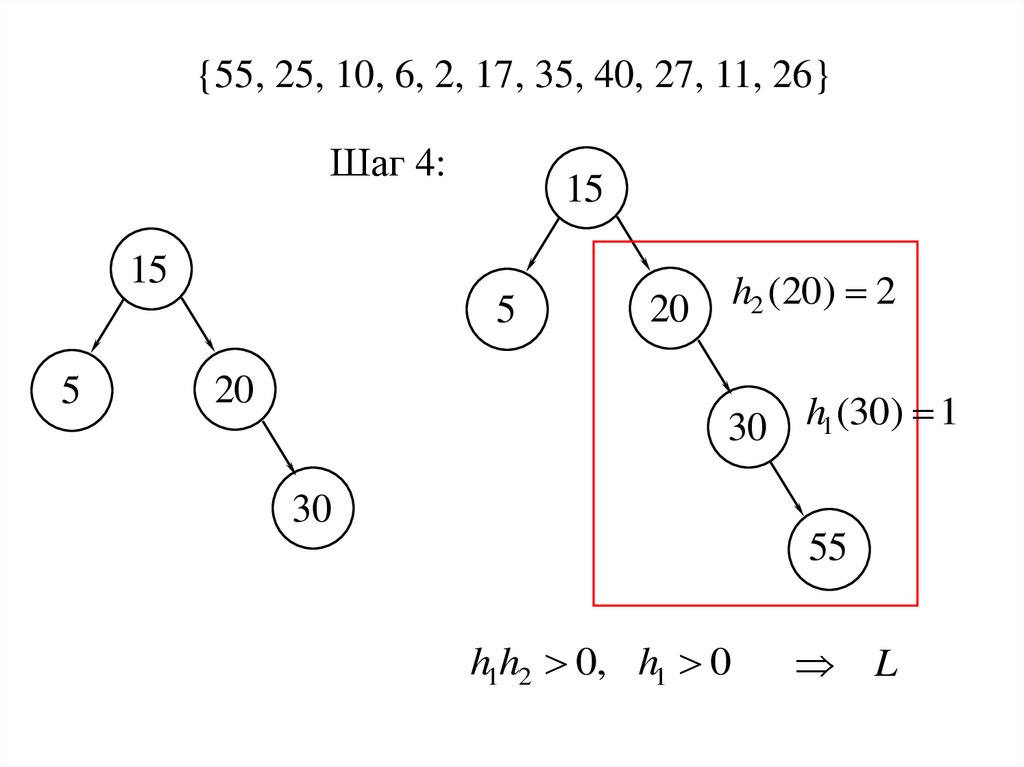
{55, 25, 10, 6, 2, 17, 35, 40, 27, 11, 26}
Шаг 4:
15
15
5
5
20
h2 (20) 2
20
30 h1 (30) 1
30
55
h1h2 0, h1 0
L

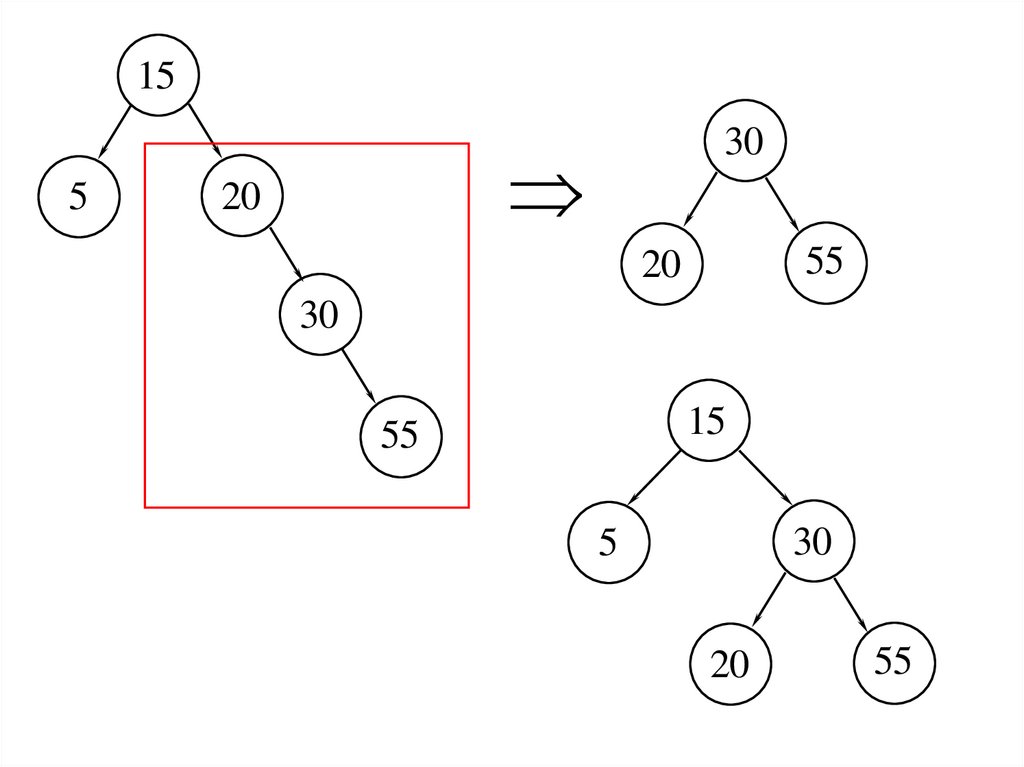
13.

15
5
30
20
55
20
30
15
55
30
5
20
55

14.

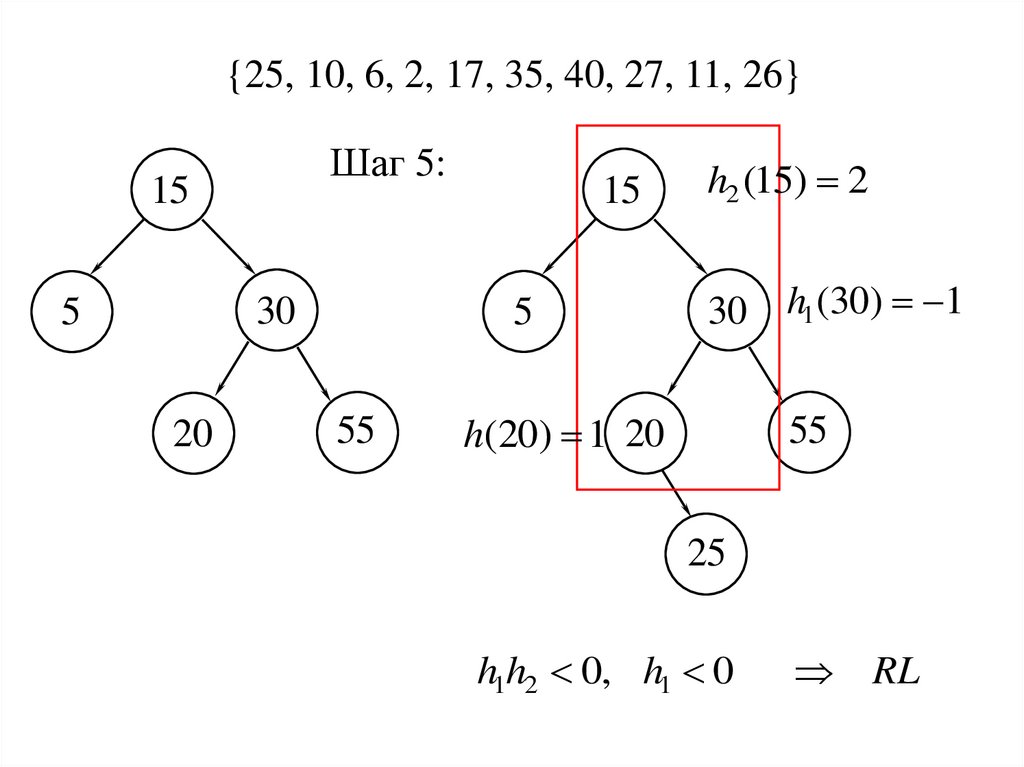
{25, 10, 6, 2, 17, 35, 40, 27, 11, 26}
Шаг 5:
15
30
5
20
15
5
55
h2 (15) 2
30 h1 (30) 1
h(20) 1 20
55
25
h1h2 0, h1 0
RL

15.

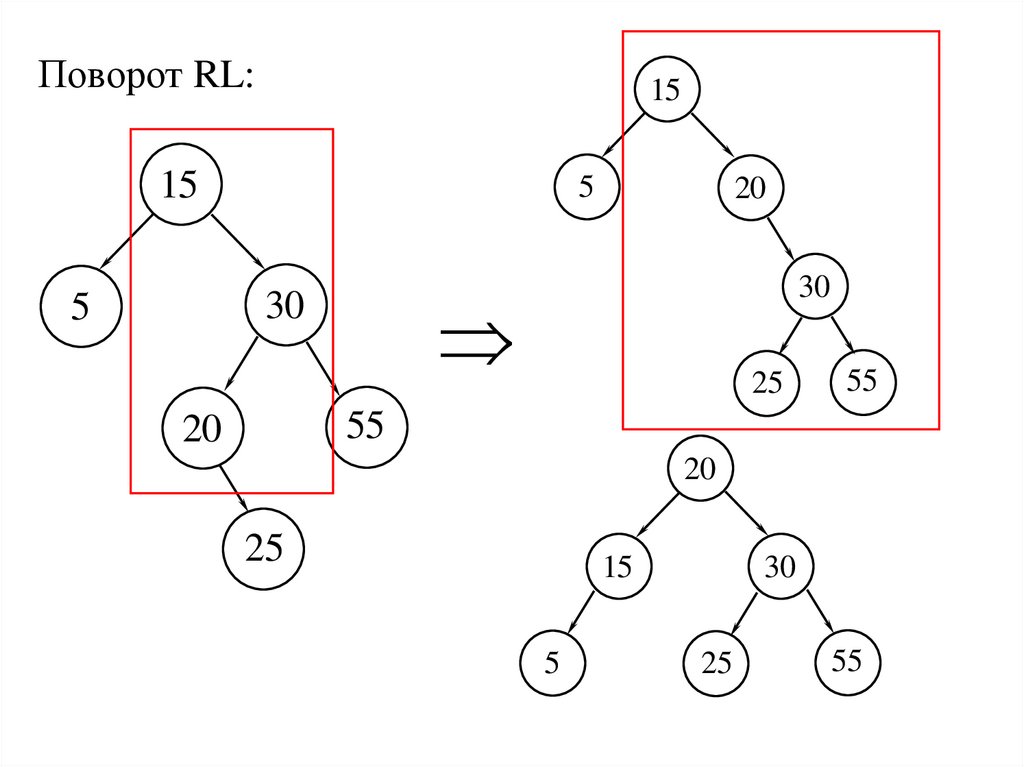
Поворот RL:
15
15
5
30
30
5
20
25
55
55
20
20
25
30
15
5
25
55

16.

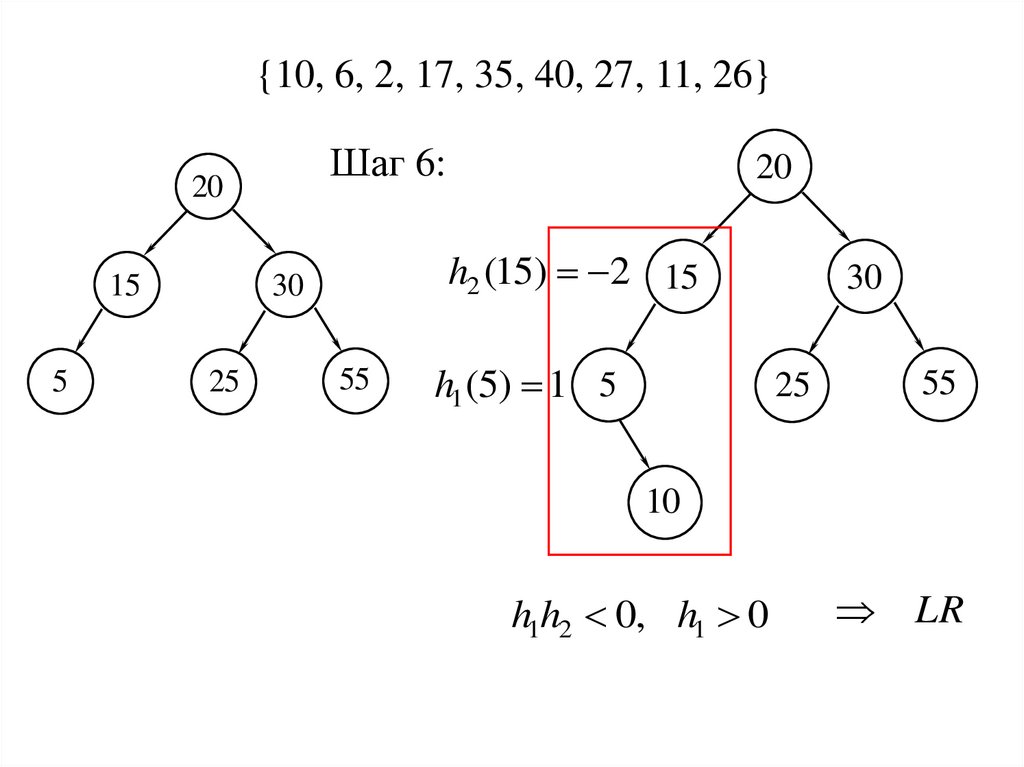
{10, 6, 2, 17, 35, 40, 27, 11, 26}
Шаг 6:
20
5
h2 (15) 2 15
30
15
25
20
55
h1 (5) 1 5
30
25
55
10
h1h2 0, h1 0
LR

17.

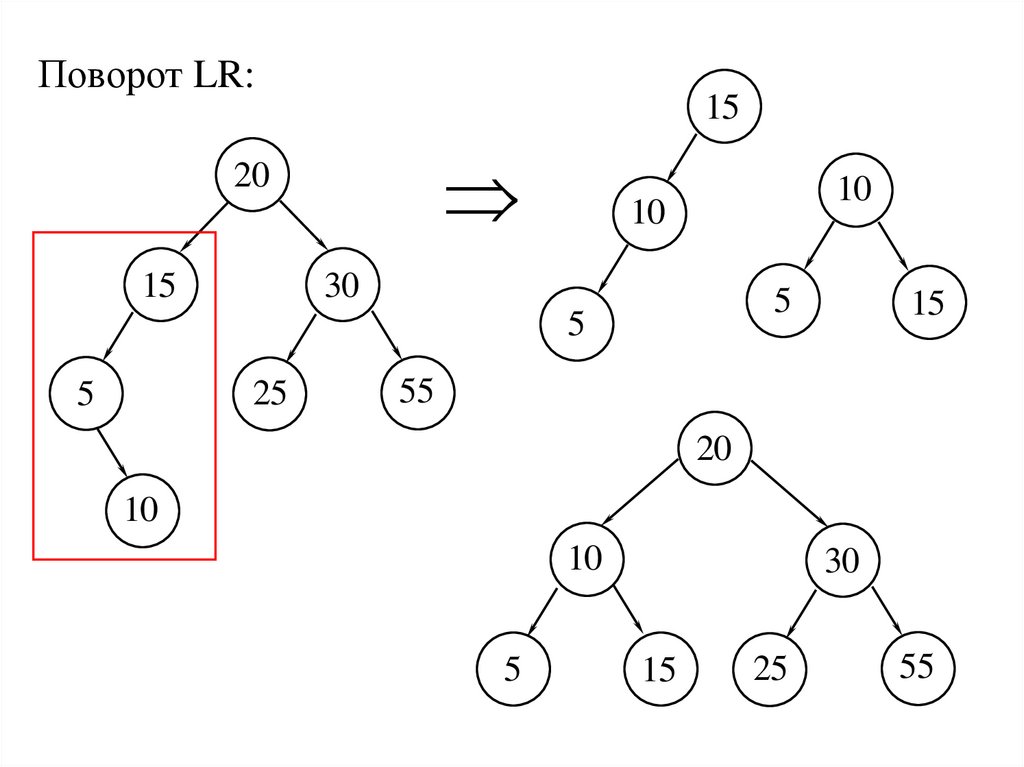
Поворот LR:
15
20
10
10
30
15
5
5
25
5
15
55
20
10
10
5
30
15
25
55

18.

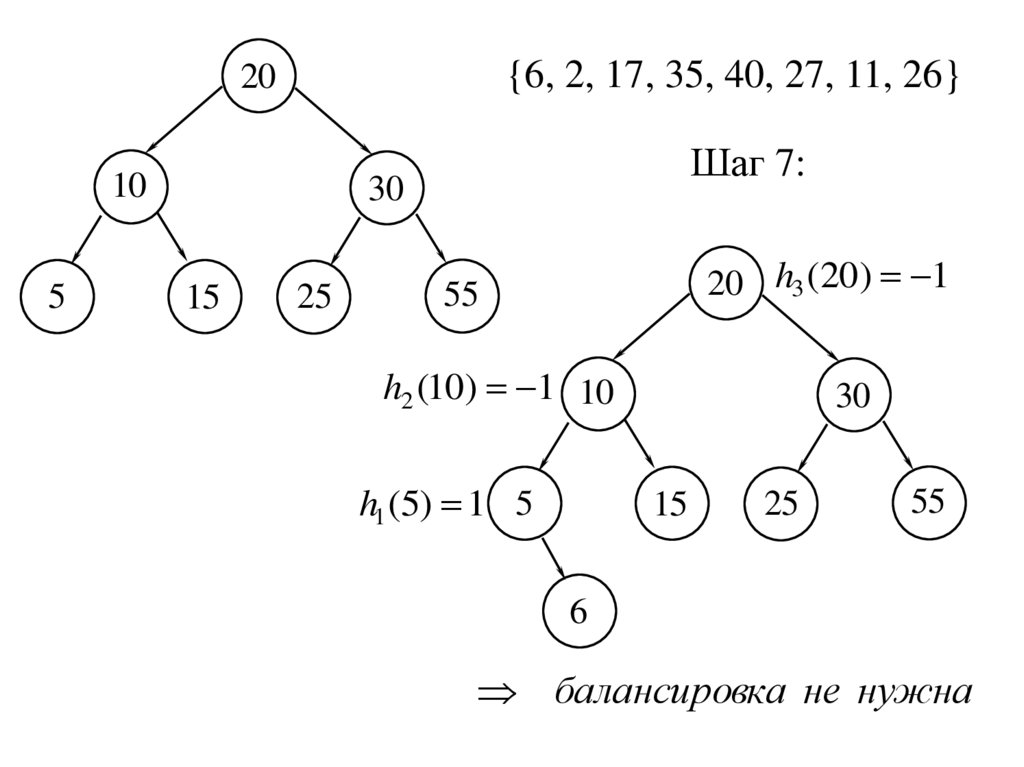
{6, 2, 17, 35, 40, 27, 11, 26}
20
10
5
Шаг 7:
30
15
25
20 h3 (20) 1
55
h2 (10) 1 10
h1 (5) 1 5
30
15
25
55
6
балансировка не нужна

19.

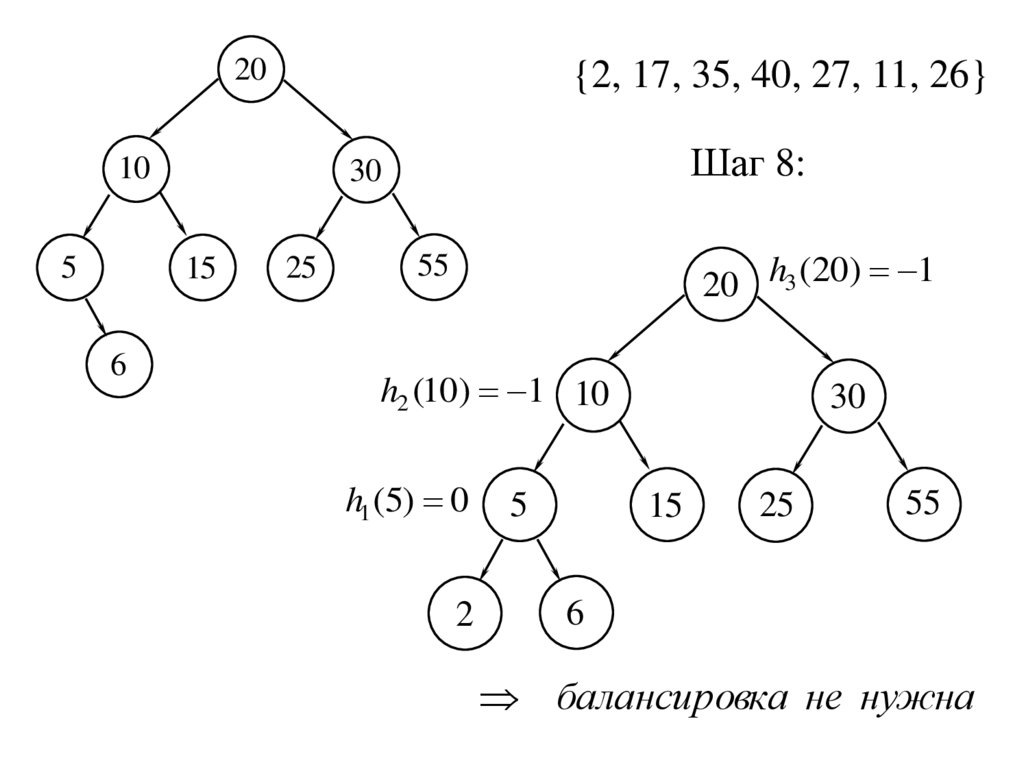
20
{2, 17, 35, 40, 27, 11, 26}
10
5
15
6
Шаг 8:
30
25
20 h3 (20) 1
55
h2 (10) 1 10
h1 (5) 0
2
5
30
15
25
55
6
балансировка не нужна

20.

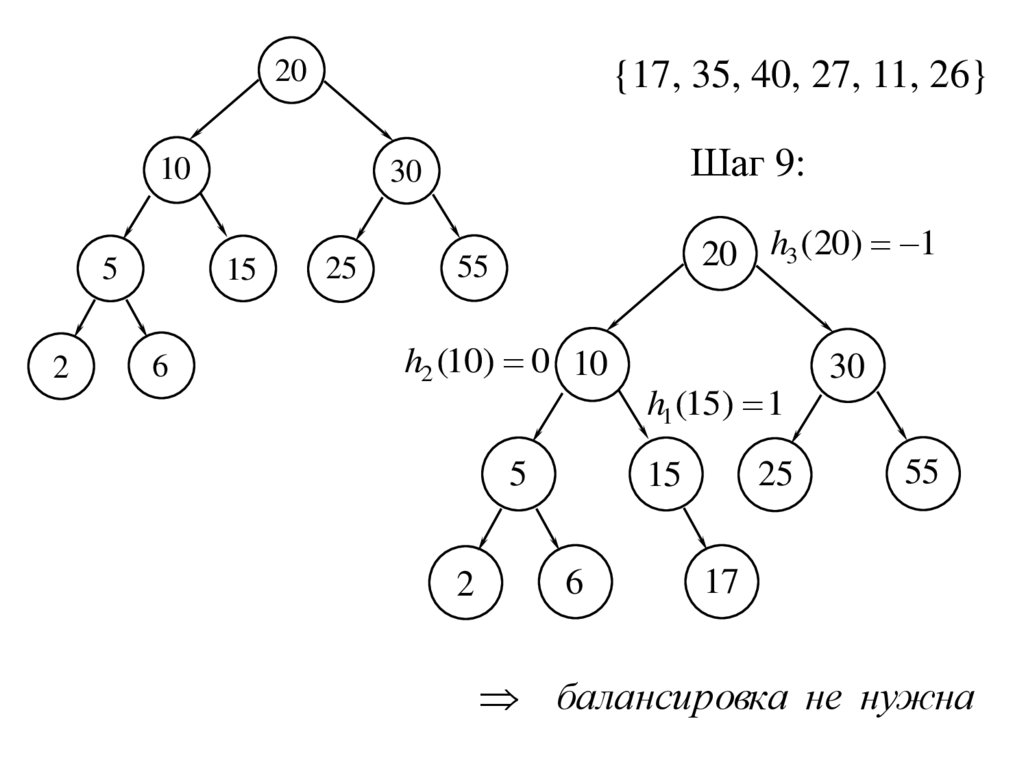
20
{17, 35, 40, 27, 11, 26}
10
5
2
15
6
Шаг 9:
30
25
20 h3 (20) 1
55
h2 (10) 0 10
5
2
h1 (15) 1
25
15
6
30
55
17
балансировка не нужна

21.

20
{35, 40, 27, 11, 26}
10
5
Шаг 10:
30
55
25
15
20
2
6
h3 (20) 0
17
h2 (30) 1
10
30
h1 (55) 1
5
2
6
55
25
15
17
35
балансировка не нужна

22.

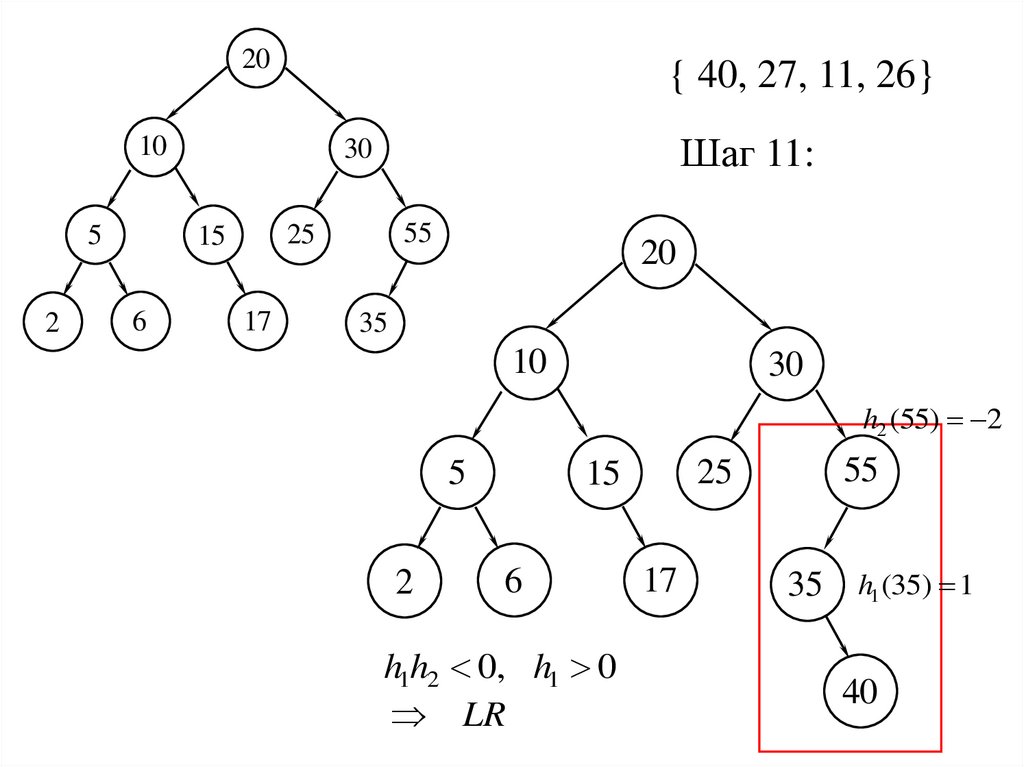
20
{ 40, 27, 11, 26}
10
5
2
55
25
15
6
Шаг 11:
30
17
20
35
10
30
h2 (55) 2
5
2
25
15
6
h1h2 0, h1 0
LR
17
55
35 h1 (35) 1
40

23.

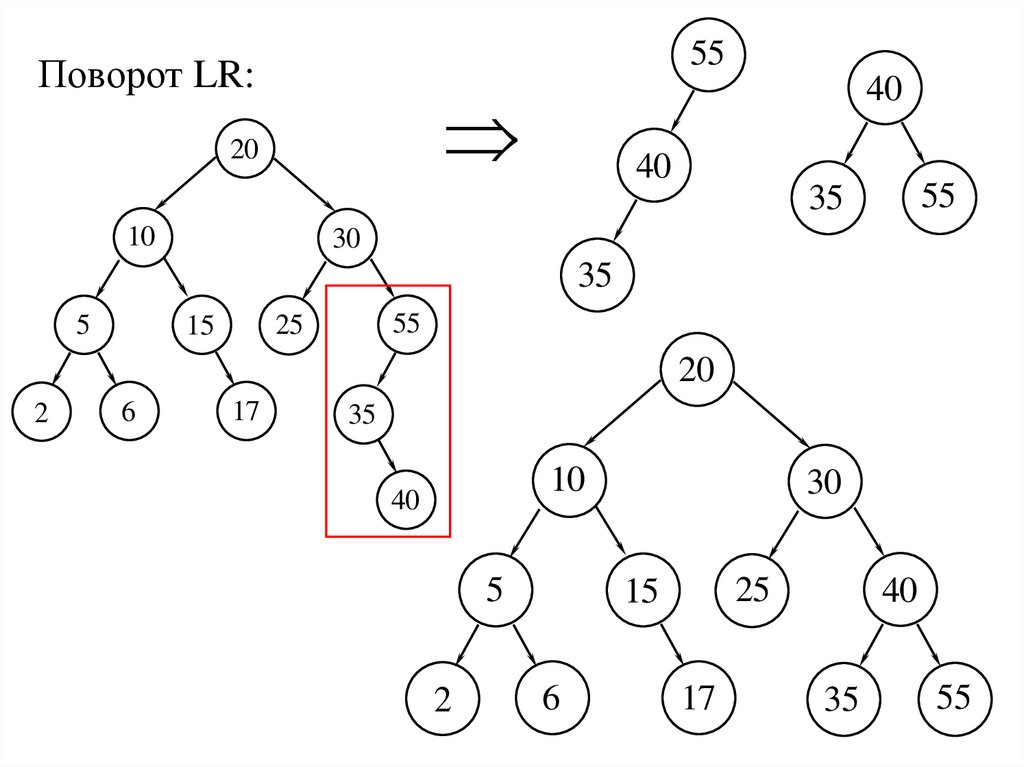
55
Поворот LR:
40
20
10
40
55
35
30
35
5
55
25
15
20
2
6
17
35
10
40
5
2
30
25
15
6
17
40
35
55

24.

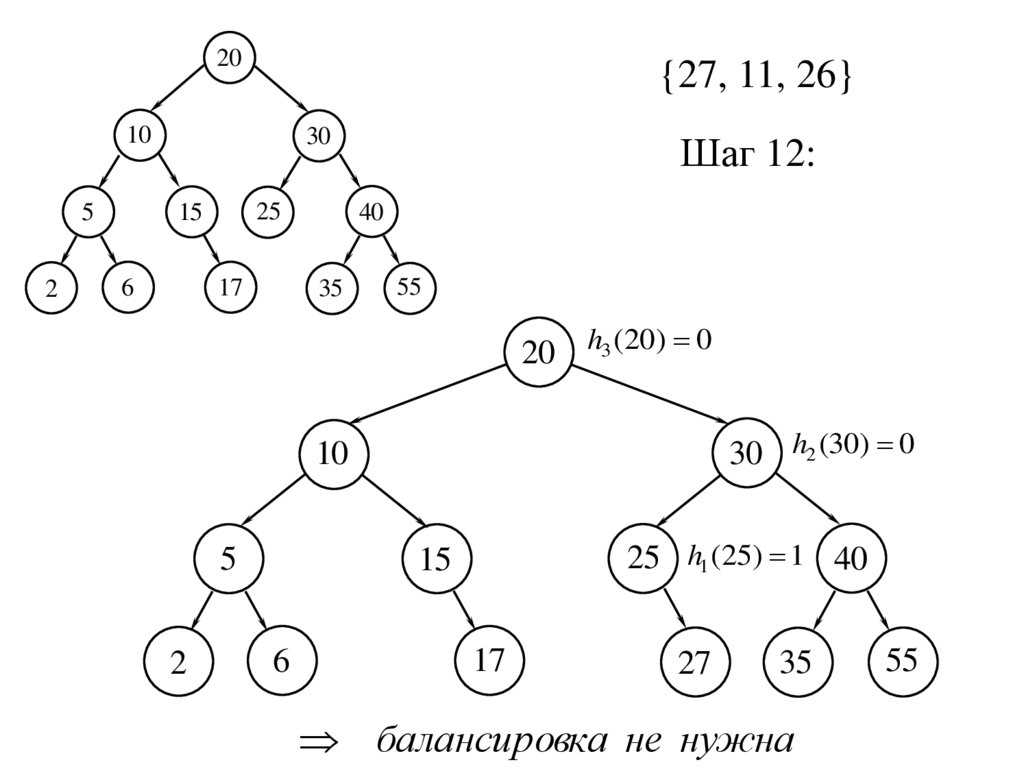
20
{27, 11, 26}
10
5
2
30
25
15
17
6
Шаг 12:
40
35
55
20 h3 (20) 0
30 h2 (30) 0
10
5
2
25 h1 (25) 1 40
15
6
17
27
35
балансировка не нужна
55

25.

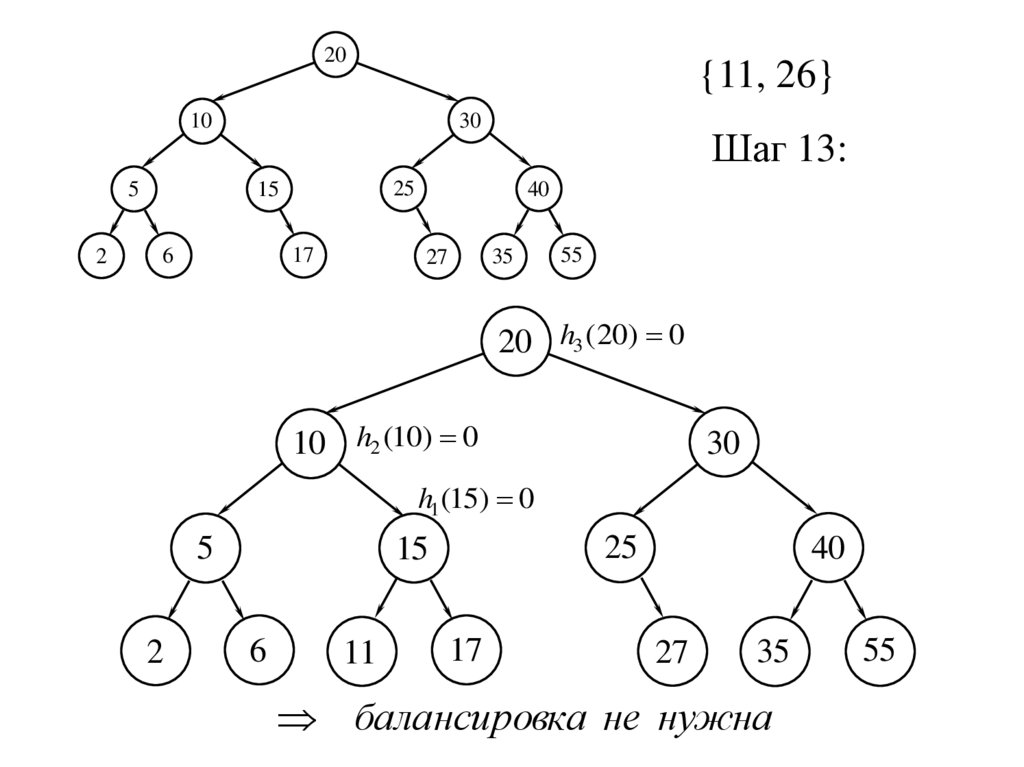
20
{11, 26}
10
5
2
30
25
15
17
6
Шаг 13:
40
35
27
55
20 h3 (20) 0
10 h2 (10) 0
30
h1 (15) 0
5
2
25
15
6
11
17
40
27
35
балансировка не нужна
55

26.

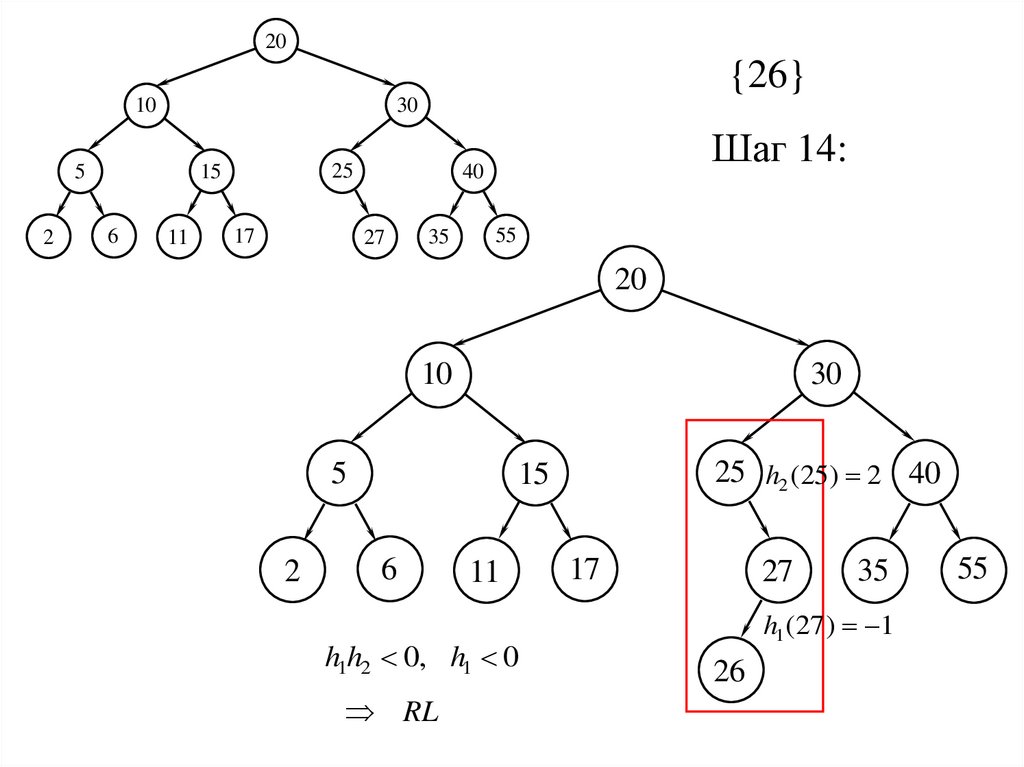
20
{26}
10
30
5
2
25
15
6
11
17
Шаг 14:
40
27
35
55
20
10
30
5
2
25 h2 (25) 2 40
15
6
11
h1h2 0, h1 0
RL
17
27
35
h1 (27 ) 1
26
55

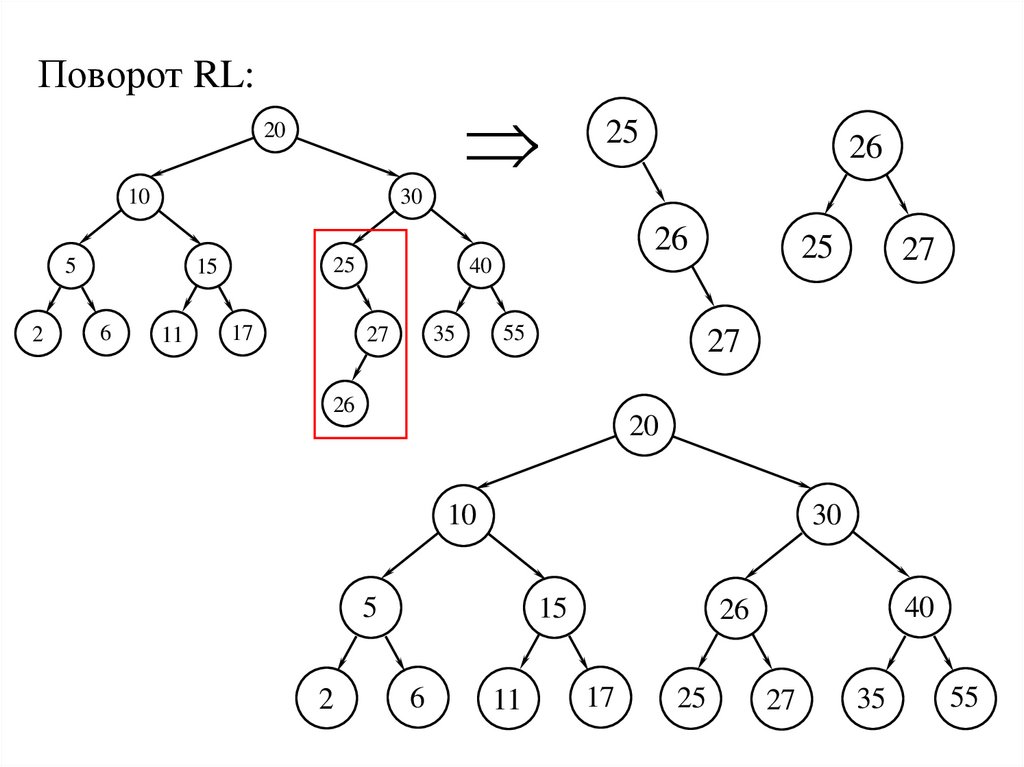
27.

Поворот RL:
20
10
11
26
25
15
6
26
30
5
2
25
17
25
40
35
27
55
27
26
20
10
30
5
2
27
15
6
11
40
26
17
25
27
35
55

28.

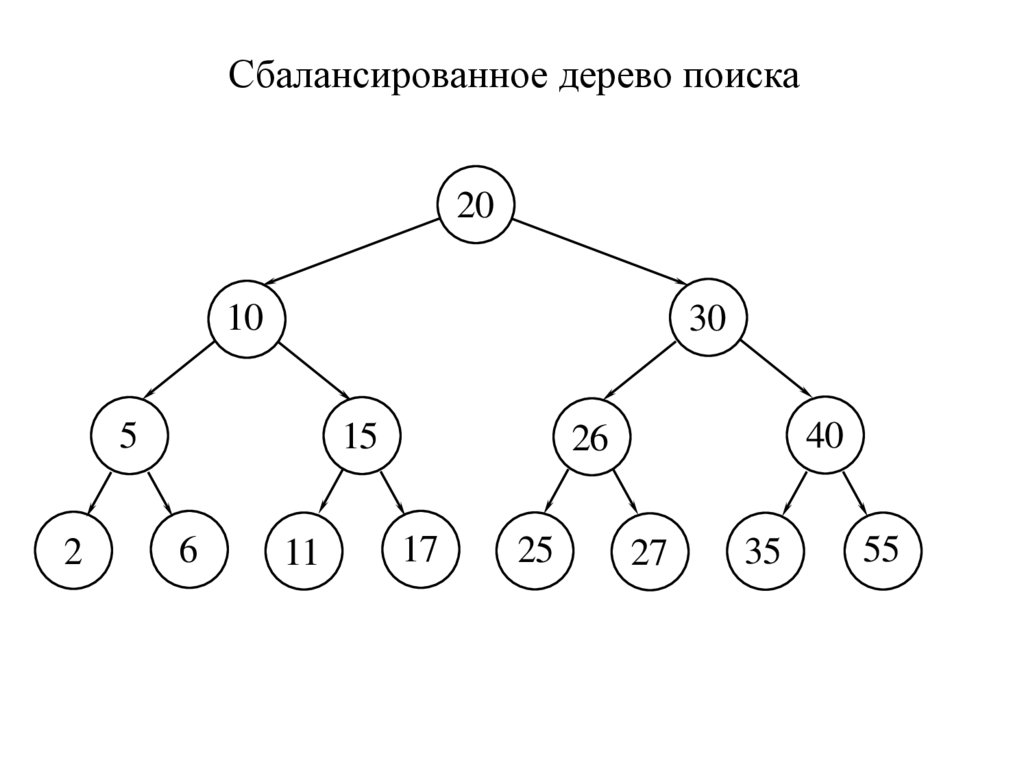
Сбалансированное дерево поиска
20
10
30
5
2
15
6
11
40
26
17
25
27
35
55