Глава 2. Деревья. Тема 2. Двоичное дерево поиска

1.

Глава 2. Деревья
п2. Двоичное дерево поиска

2.

Определение двоичного дерева поиска
Двоичное дерево называется деревом поиска, если
для каждого узла дерева выполняется условие:
значение ключа в узле
больше значений ключей в левом поддереве и
меньше значений ключей в правом поддереве
2

3.

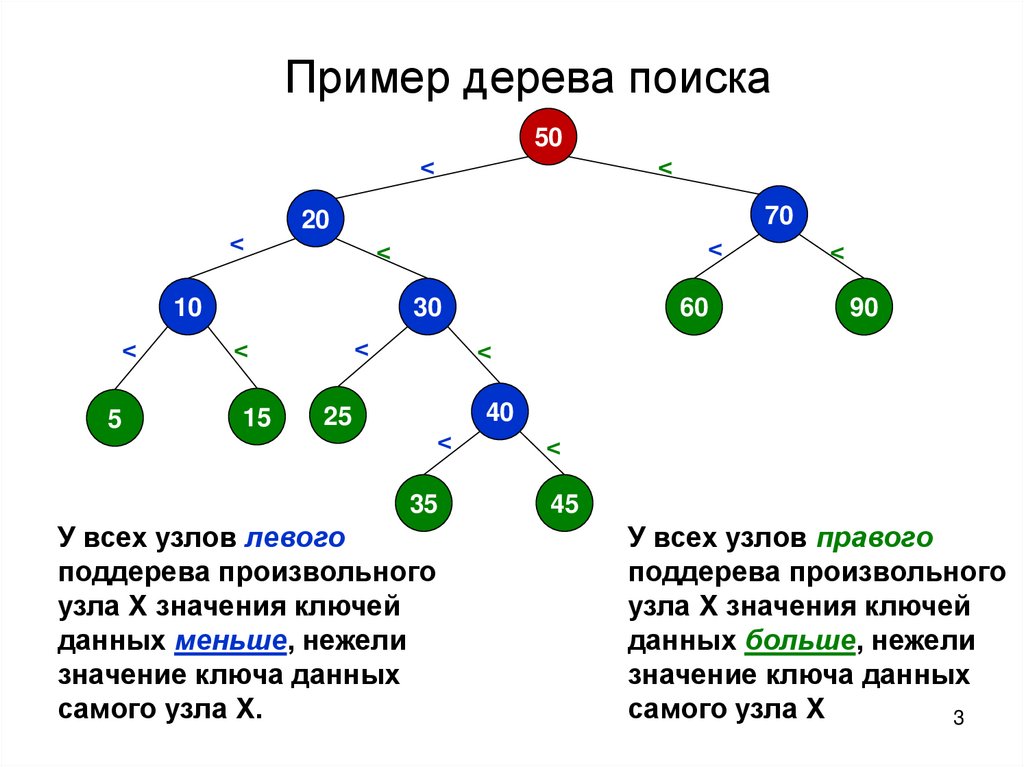
Пример дерева поиска
50
<
<
<
70
20
<
<
10
30
<
<
5
15
<
60
<
90
<
40
25
<
<
35
45
У всех узлов левого
поддерева произвольного
узла X значения ключей
данных меньше, нежели
значение ключа данных
самого узла X.
У всех узлов правого
поддерева произвольного
узла X значения ключей
данных больше, нежели
значение ключа данных
самого узла X
3

4.

Операции над деревьями поиска
Основные операции при работе с деревьями поиска не
отличаются от обычного двоичного дерева:
- Добавление узла
- Удаление узла
- Поиск узла
- Обход узлов
Главное требование при выполнении этих операций –
сохранение указанного выше свойства двоичного
дерева поиска:
значение ключа в узле
больше значений ключей в левом поддереве и
меньше значений ключей в правом поддереве
4

5.

Добавление узла в дерево поиска
1. Если корень поддерева пуст, поместить в
него заданный ключ; закончить алгоритм.
2. Если новый ключ меньше ключа корня:
перейти в левое поддерево и повторить с п.1.
3. Иначе, перейти в правое поддерево и
повторить с п.1.
Замечание:
при
равенстве
ключей
в
зависимости от конкретной задачи можно либо
выйти и не помещать такое же значение, либо
поместить, переходя, например, вправо (как
будет далее).
5

6.

Добавление узла в дерево поиска
//ToDo: сделать метод родителя виртуальным
Node *addNode(Node *root, int key) override
{
if (!root) {
root = new Node(key);
} else if (key < root->key()) {
root->setLeftChild(addNode(root->leftChild(), key));
} else {
root->setRightChild(addNode(root->rightChild(), key));
}
return root;
}
6

7.

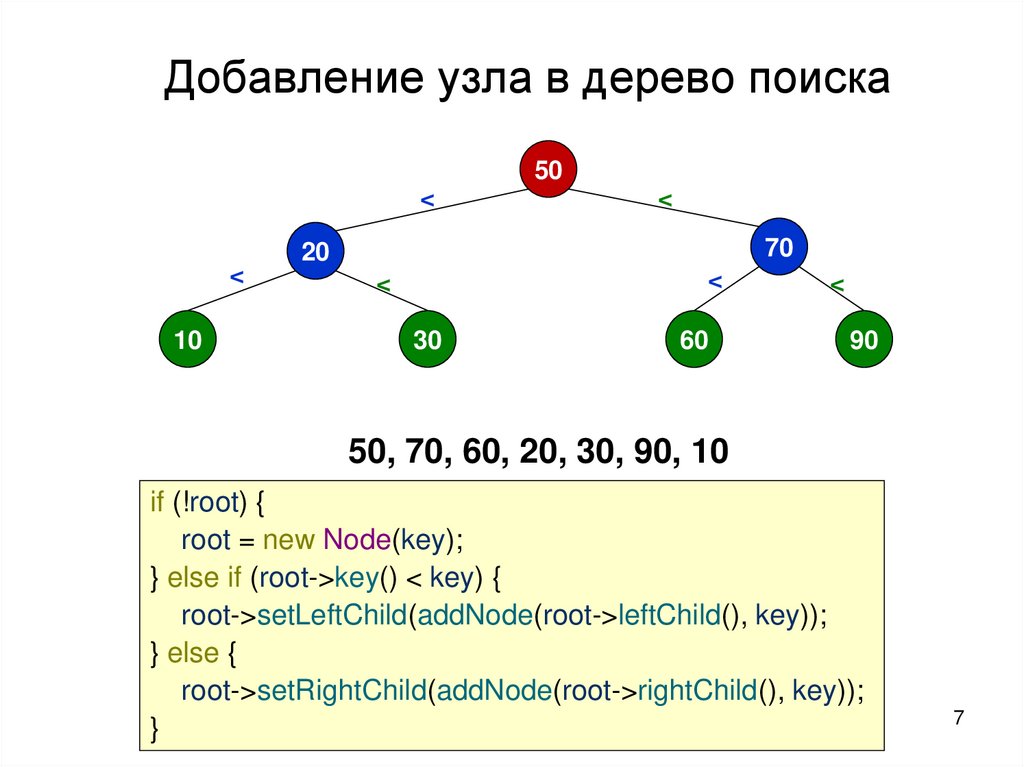
Добавление узла в дерево поиска
50
<
<
10
<
70
20
<
<
30
60
<
90
50, 70, 60, 20, 30, 90, 10
if (!root) {
root = new Node(key);
} else if (root->key() < key) {
root->setLeftChild(addNode(root->leftChild(), key));
} else {
root->setRightChild(addNode(root->rightChild(), key));
}
7

8.

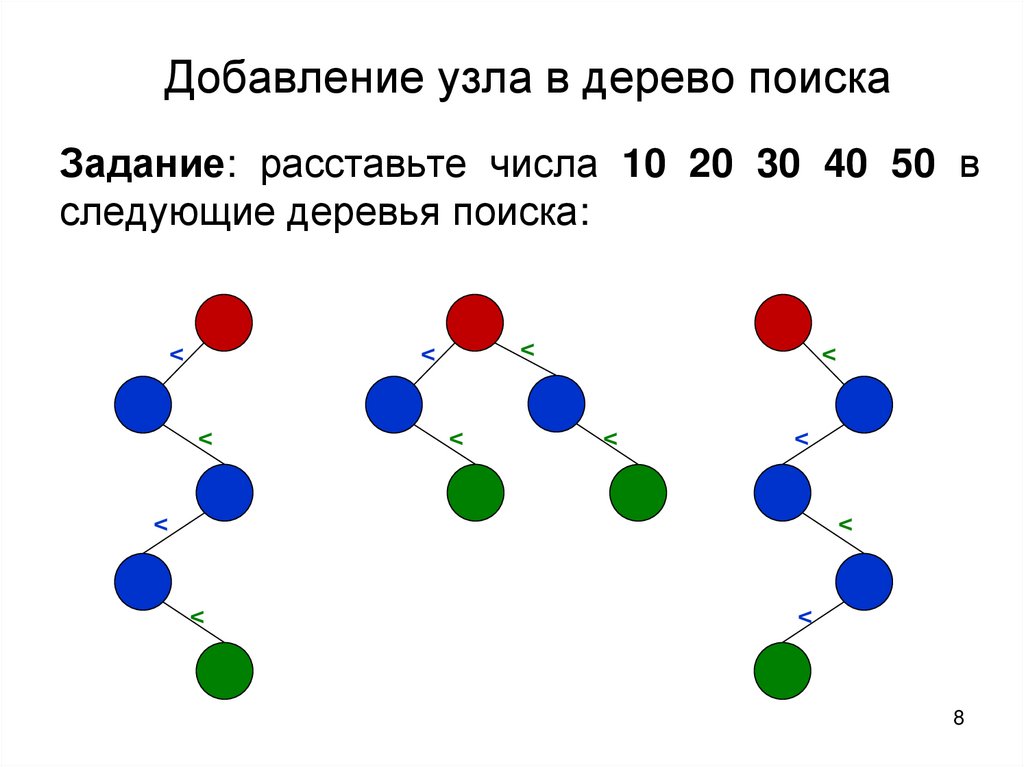
Добавление узла в дерево поиска
Задание: расставьте числа 10 20 30 40 50 в
следующие деревья поиска:
30
50
<
<
10
10
<
<
40
10
<
<
40
20
50
<
<
50
20
<
<
20
40
<
<
30
30
8

9.

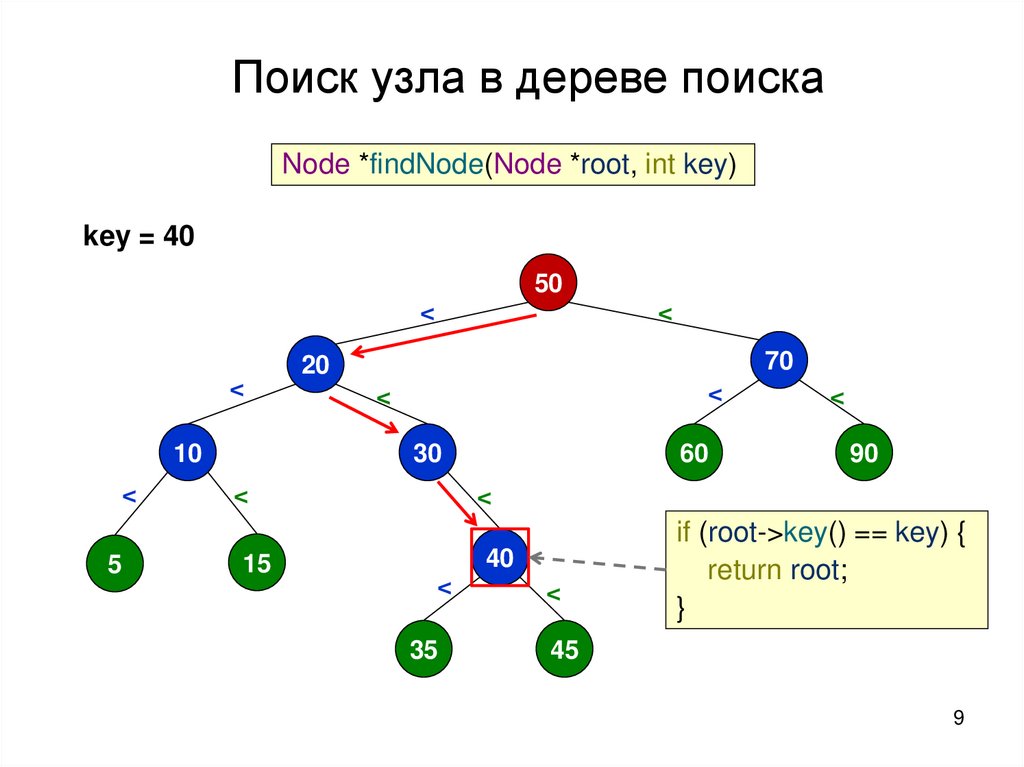
Поиск узла в дереве поиска
Node *findNode(Node *root, int key)
key = 40
50
<
<
10
<
5
<
70
20
<
<
30
<
15
60
<
90
<
40
<
<
35
45
if (root->key() == key) {
return root;
}
9

10.

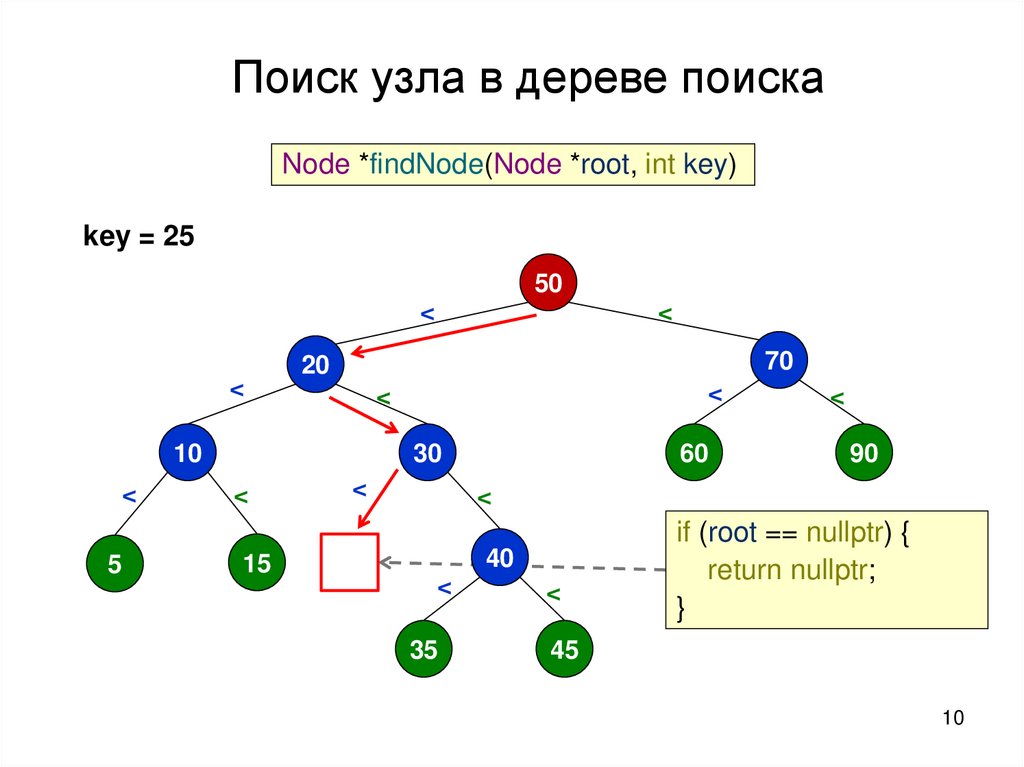
Поиск узла в дереве поиска
Node *findNode(Node *root, int key)
key = 25
50
<
<
70
20
5
<
<
10
<
<
30
<
15
<
60
<
90
<
40
<
<
35
45
if (root == nullptr) {
return nullptr;
}
10

11.

Удаление узла из дерева поиска
Аналогично двоичному дереву, при удалении узла из
дерева поиска возможны три случая:
1. Удаляемый узел не имеет поддеревьев (лист);
2. Удаляемый узел имеет одно поддерево;
3. Удаляемый узел имеет оба поддерева.
Первые два случая по реализации ничем не отличаются
от рассмотренных в прошлый раз для обычного
двоичного дерева, т.к. правило дерева поиска не
нарушается.
Если удаляемый узел имеет оба поддерева,
рекомендуется заменить его узлом, ключ в котором
наиболее близок по значению (т.е. либо больше любого
ключа в левом поддереве, либо меньше любого в
11
правом)

12.

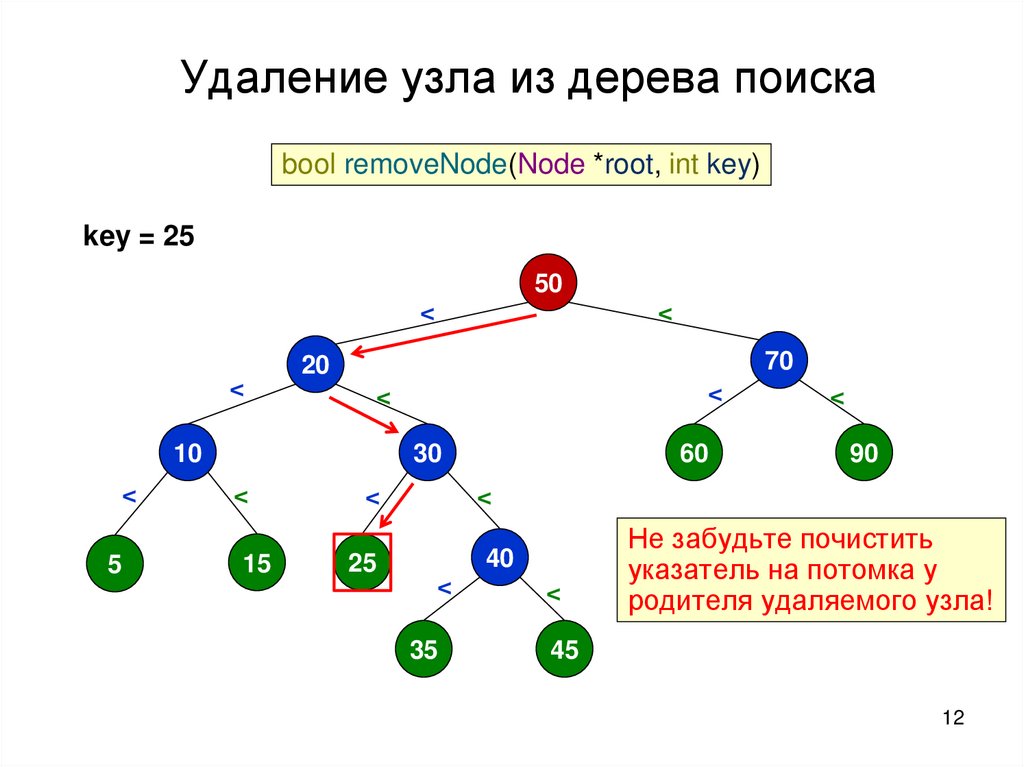
Удаление узла из дерева поиска
bool removeNode(Node *root, int key)
key = 25
50
<
<
70
20
5
<
<
10
<
<
30
<
15
60
<
<
25
40
<
<
35
45
<
90
Не забудьте почистить
указатель на потомка у
родителя удаляемого узла!
12

13.

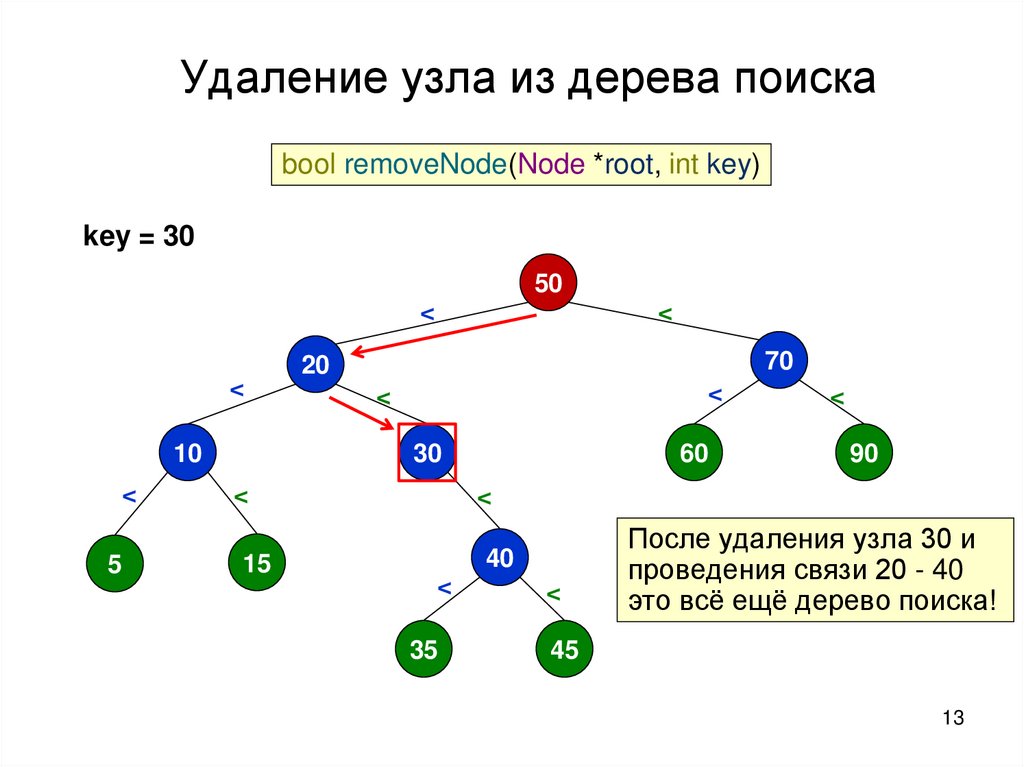
Удаление узла из дерева поиска
bool removeNode(Node *root, int key)
key = 30
50
<
<
10
<
5
<
70
20
<
<
30
60
<
<
15
40
<
<
35
45
<
90
После удаления узла 30 и
проведения связи 20 - 40
это всё ещё дерево поиска!
13

14.

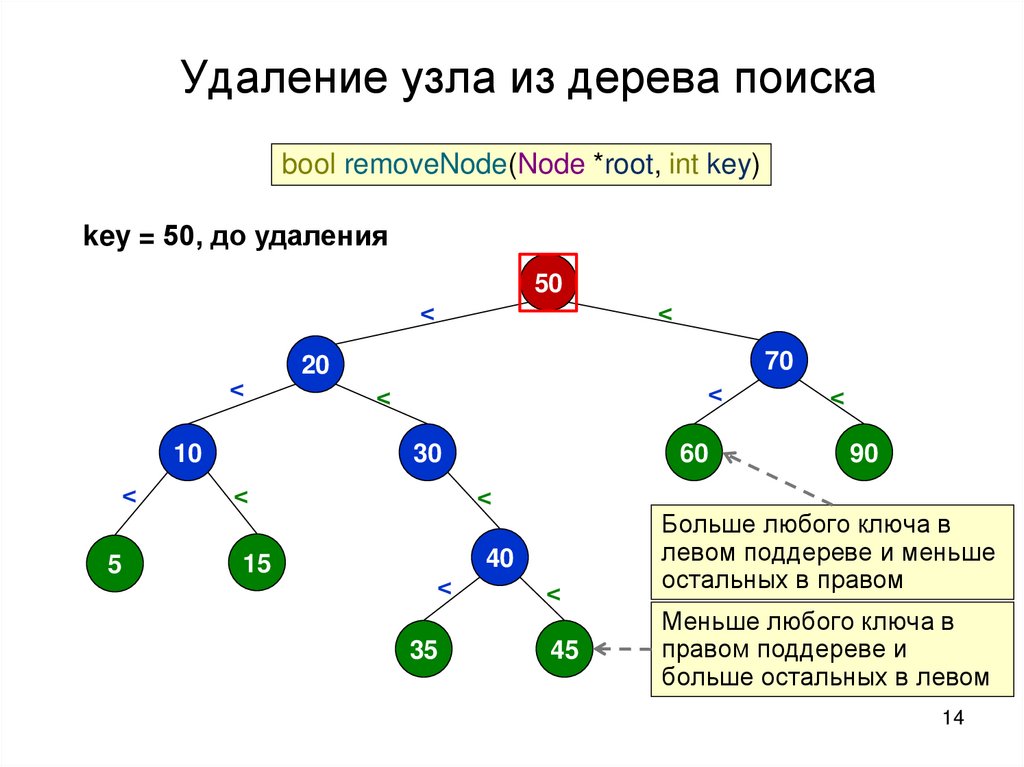
Удаление узла из дерева поиска
bool removeNode(Node *root, int key)
key = 50, до удаления
50
<
<
10
<
5
<
70
20
<
<
30
<
15
60
<
40
<
35
<
45
<
90
Больше любого ключа в
левом поддереве и меньше
остальных в правом
Меньше любого ключа в
правом поддереве и
больше остальных в левом
14

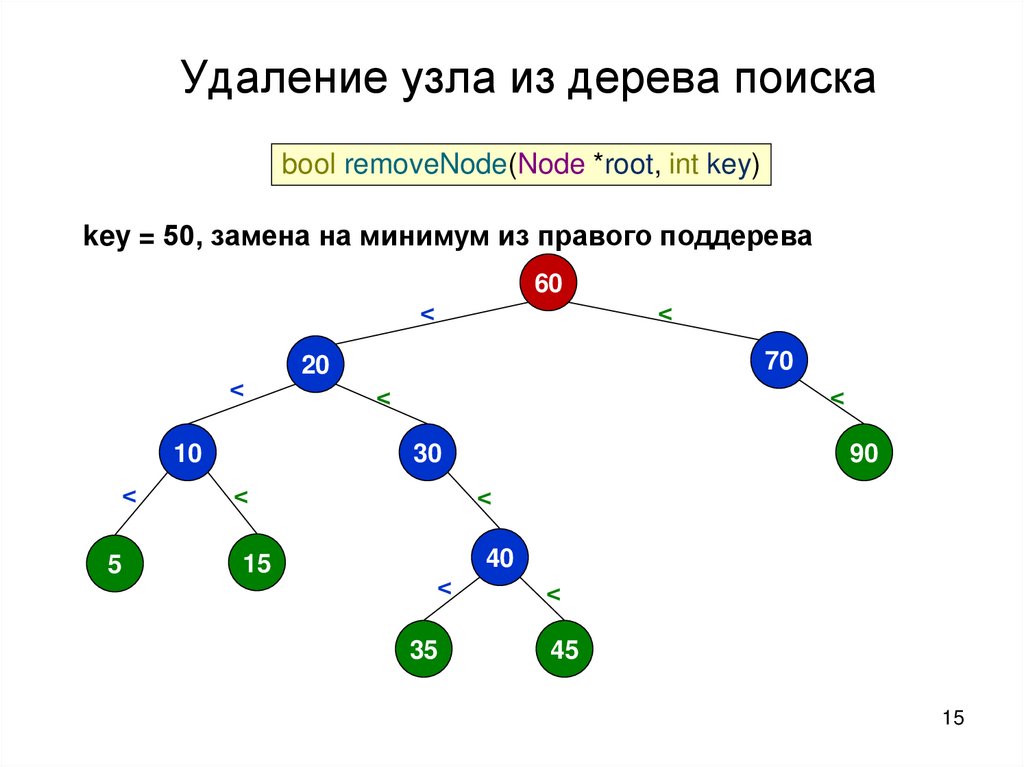
15.

Удаление узла из дерева поиска
bool removeNode(Node *root, int key)
key = 50, замена на минимум из правого поддерева
60
<
<
10
<
70
20
<
<
30
90
<
<
<
5
15
40
<
<
35
45
15

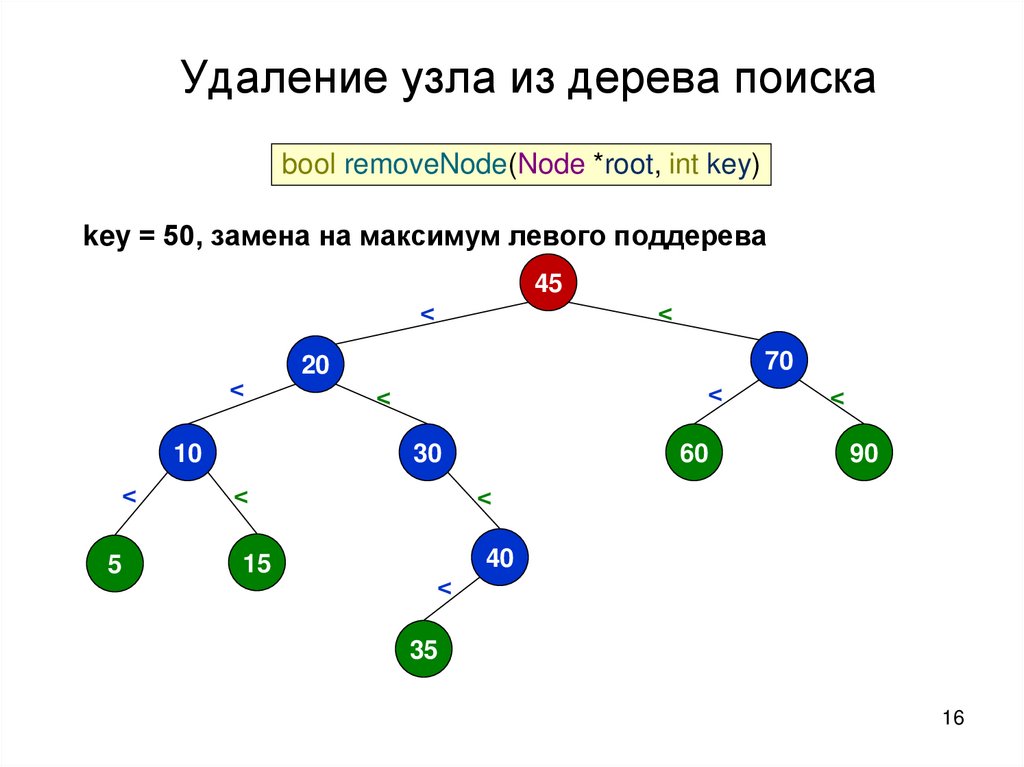
16.

Удаление узла из дерева поиска
bool removeNode(Node *root, int key)
key = 50, замена на максимум левого поддерева
45
<
<
10
<
70
20
<
<
30
60
<
<
<
5
15
40
<
90
<
35
16

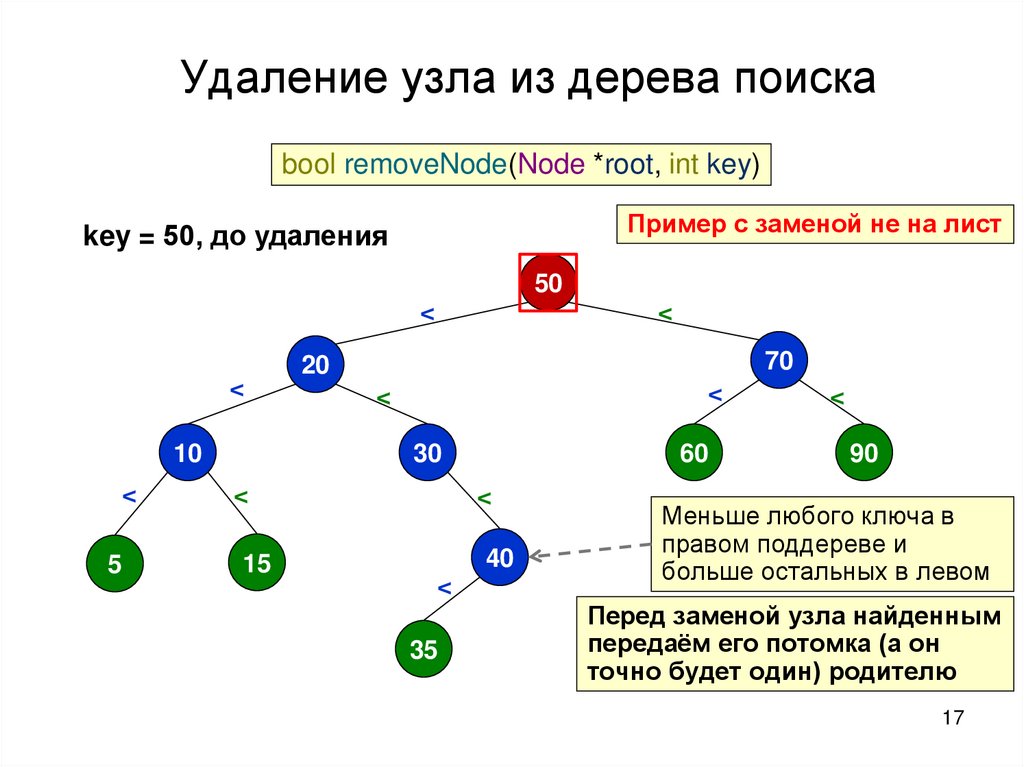
17.

Удаление узла из дерева поиска
bool removeNode(Node *root, int key)
Пример с заменой не на лист
key = 50, до удаления
50
<
<
10
<
70
20
<
<
30
60
<
<
<
5
15
40
<
35
<
90
Меньше любого ключа в
правом поддереве и
больше остальных в левом
Перед заменой узла найденным
передаём его потомка (а он
точно будет один) родителю
17

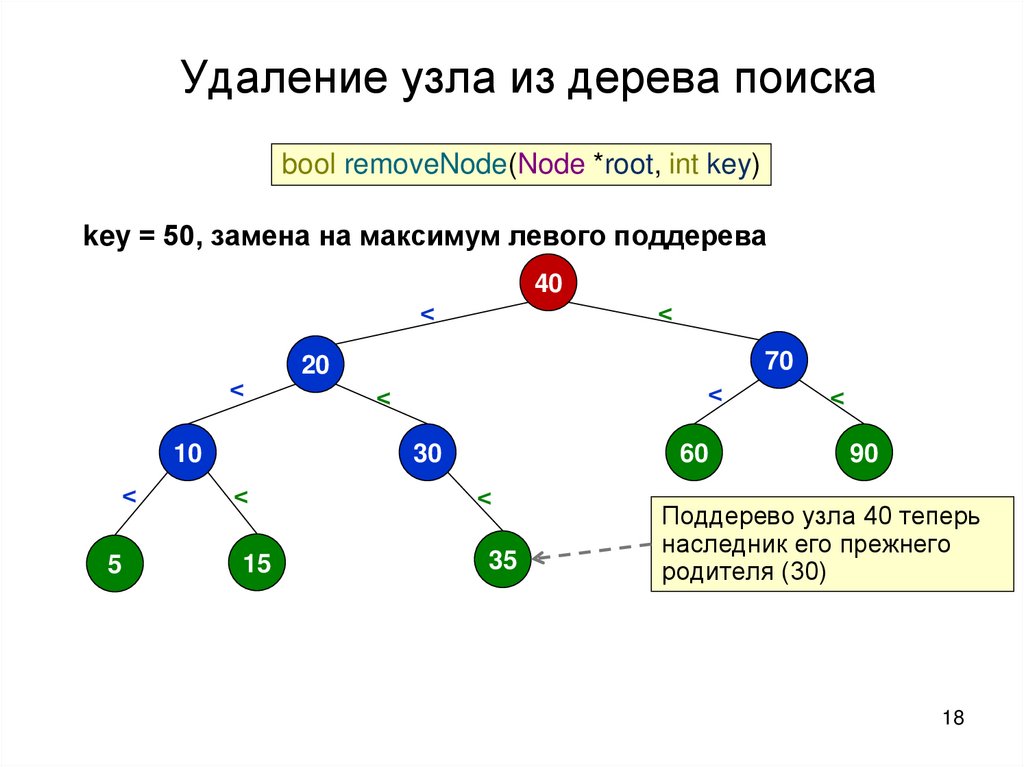
18.

Удаление узла из дерева поиска
bool removeNode(Node *root, int key)
key = 50, замена на максимум левого поддерева
40
<
<
10
<
70
20
<
<
30
60
<
<
<
5
15
35
<
90
Поддерево узла 40 теперь
наследник его прежнего
родителя (30)
18

19.

Удаление узла из дерева поиска
Алгоритм определения узла r, который заменит
удаляемый узел n:
1. Тривиальные случаи: у n есть только один потомок.
Тогда r равен этому потомку. Алгоритм окончен,
дополнительных действий не требуется.
2. Спуск по правой ветви: r = n->rightChild().
3. Если r->leftChild() == nullptr, замена найдена.
Установить левого потомка n в качестве левого
потомка r. Алгоритм окончен.
4. Поиск в поддереве с корнем r->leftChild() узла, у
которого нет левого потомка (далее r указывает на
найденный узел, rp указывает на его родителя).
5. Передаём правое поддерево узла r его родителю:
rp->setLeftChild(r->rightChild());
6. Передаём потомков узла n узлу r. Алгоритм окончен.
Всё, что останется для завершения удаления – заменить n на r в
родителе n и очистить память n.
19

20.

Удаление узла из дерева поиска
Замечание: аналогично можно выполнить
удаление ключа, спускаясь по левой ветви от n
и найдя самый правый узел (с пустым правым
потомком), т.е. поиск наиболее близкого ключа с
меньшим значением, чем n->key(). Далее
выполнить симметричные действия.
Замечание 2: т.к. при поиске потомка спуск
всегда происходит только по одной ветви
(левой/правой), он легко реализуется обычным
циклом.
20

21.

Использование функции удаления
Пусть функция удаления узла имеет сигнатуру:
Node *removeNode(Node *node)
И удаляет переданный узел, возвращая
указатель на узел, который его заменил.
Как применить эту функцию для удаления всех
узлов с чётными ключами из поддерева?
21

22.

Использование функции удаления
Node *removeEvenNodes(Node *root)
{
if (root == nullptr) {
return nullptr;
}
root->setLeftChild(removeEvenNodes(root->leftChild()));
root->setRightChild(removeEvenNodes(root->rightChild()));
if (root->key() % 2 == 0) {
return removeNode(root);
}
return root;
}
22

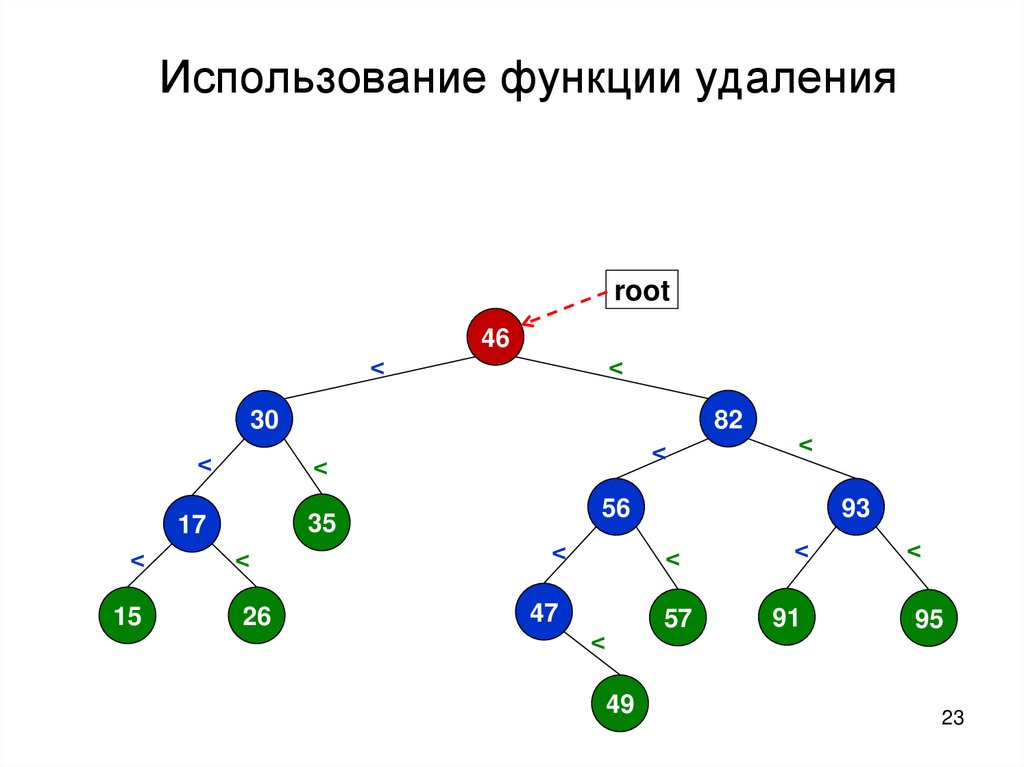
23.

Использование функции удаления
root
46
<
<
82
30
<
<
17
35
<
<
56
<
<
<
15
26
47
<
49
93
<
<
<
57
91
95
23

24.

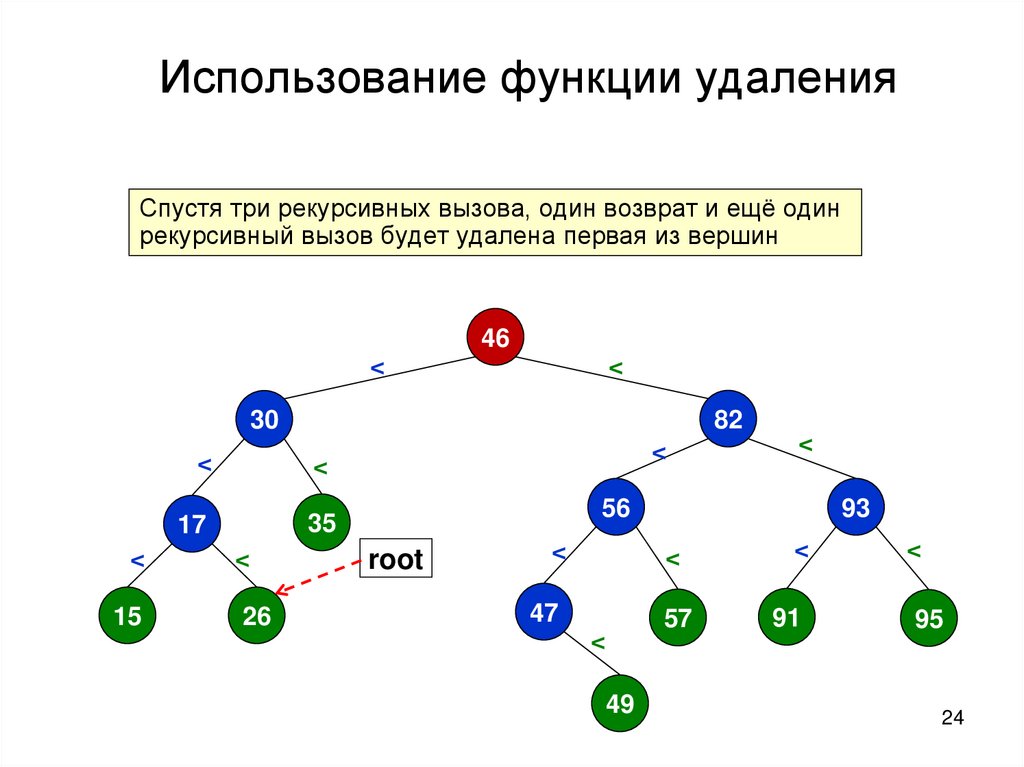
Использование функции удаления
Спустя три рекурсивных вызова, один возврат и ещё один
рекурсивный вызов будет удалена первая из вершин
46
<
<
82
30
<
<
17
35
<
<
15
26
<
<
56
root
<
47
<
49
93
<
<
<
57
91
95
24

25.

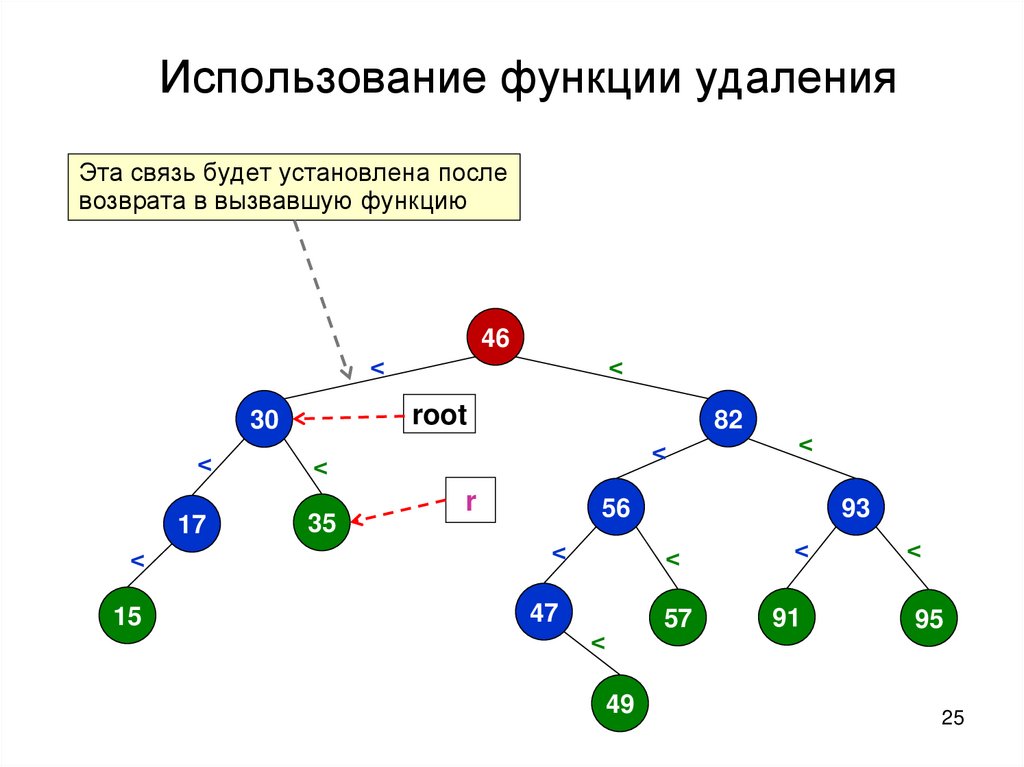
Использование функции удаления
Эта связь будет установлена после
возврата в вызвавшую функцию
46
<
<
root
30
<
17
82
<
<
35
r
<
56
<
<
15
47
<
49
93
<
<
<
57
91
95
25

26.

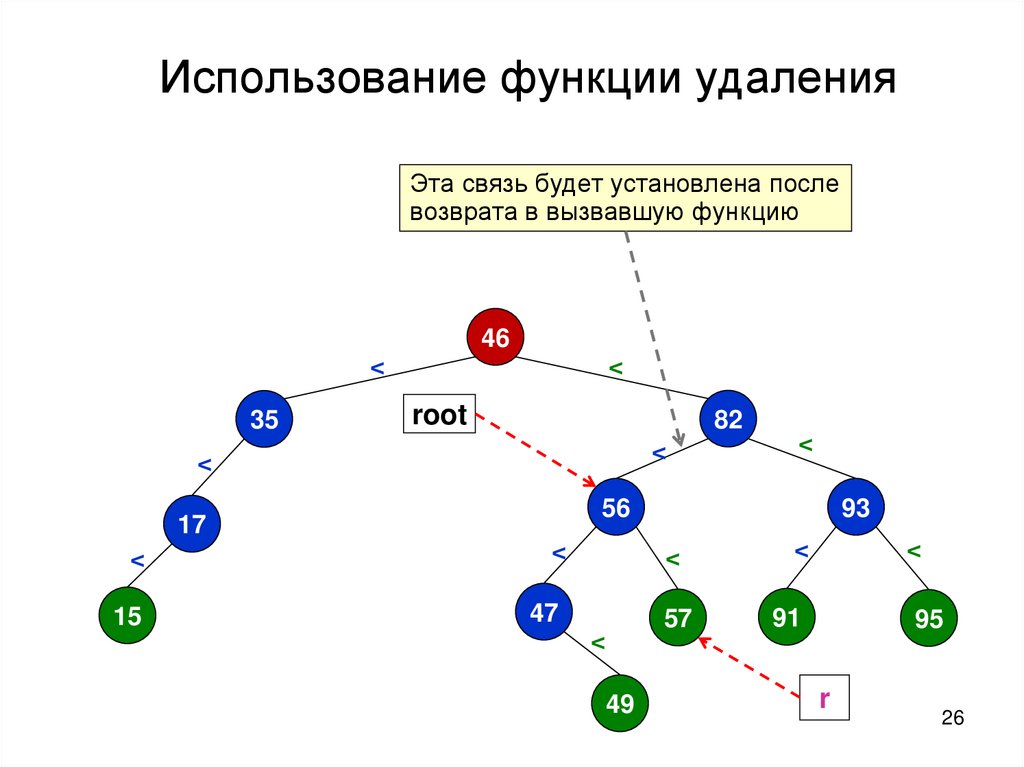
Использование функции удаления
Эта связь будет установлена после
возврата в вызвавшую функцию
46
<
<
35
root
82
<
<
<
56
17
<
<
15
47
<
49
93
<
<
<
57
91
95
r
26

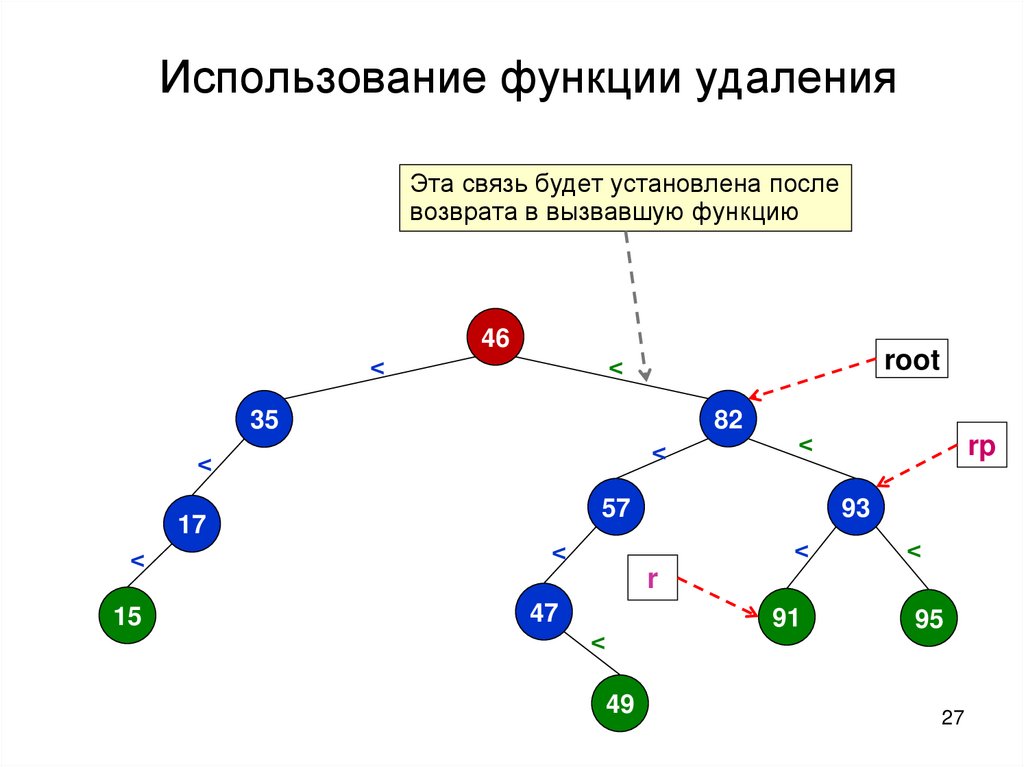
27.

Использование функции удаления
Эта связь будет установлена после
возврата в вызвавшую функцию
46
root
<
<
82
35
<
<
<
57
17
<
<
15
47
rp
93
<
<
91
95
r
<
49
27

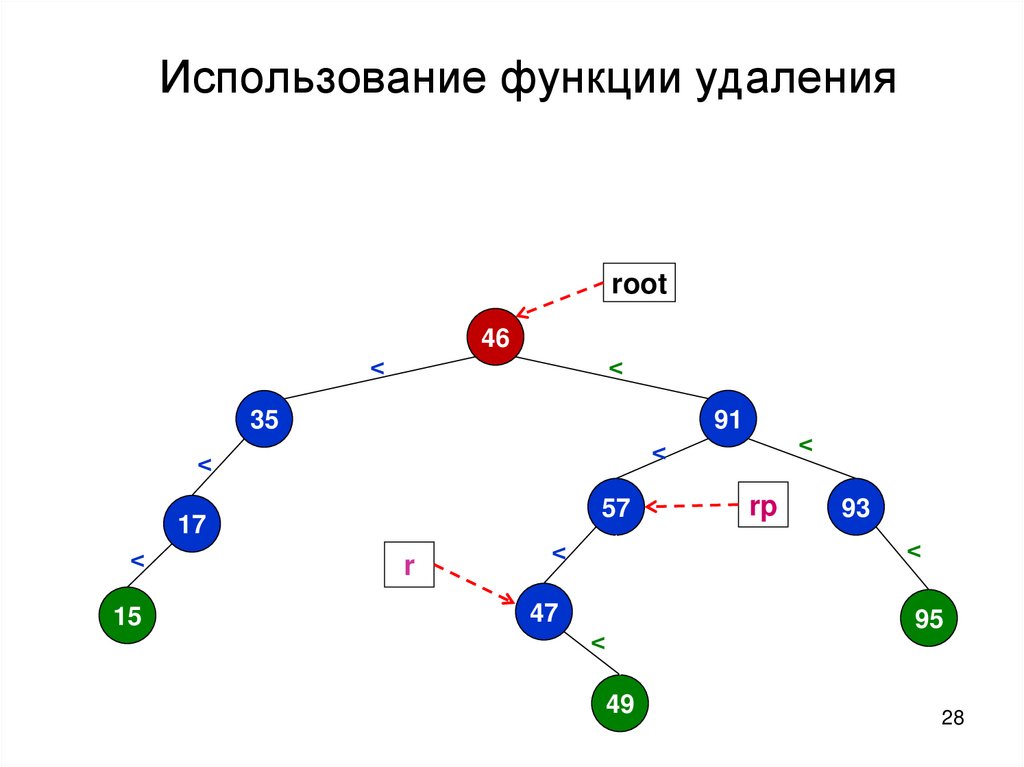
28.

Использование функции удаления
root
46
<
<
91
35
57
17
<
15
<
<
<
r
93
<
<
47
rp
<
<
49
95
28

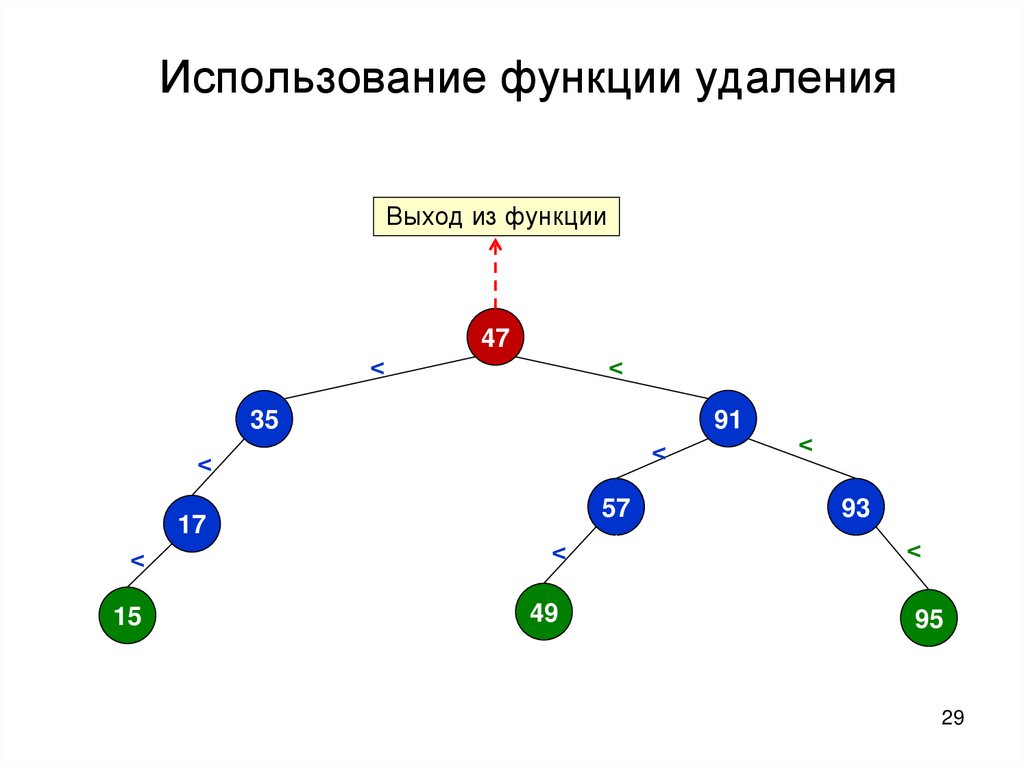
29.

Использование функции удаления
Выход из функции
47
<
<
91
35
<
<
57
17
<
<
15
49
<
93
<
<
95
29

30.

Обход дерева поиска
Обход дерева поиска может выполняться по тем
же правилам, что и обход любого двоичного
дерева:
К-Л-П, К-П-Л, Л-К-П, П-К-Л, Л-П-К, по уровням.
Рассмотрим обход Л-К-П для дерева поиска.
30

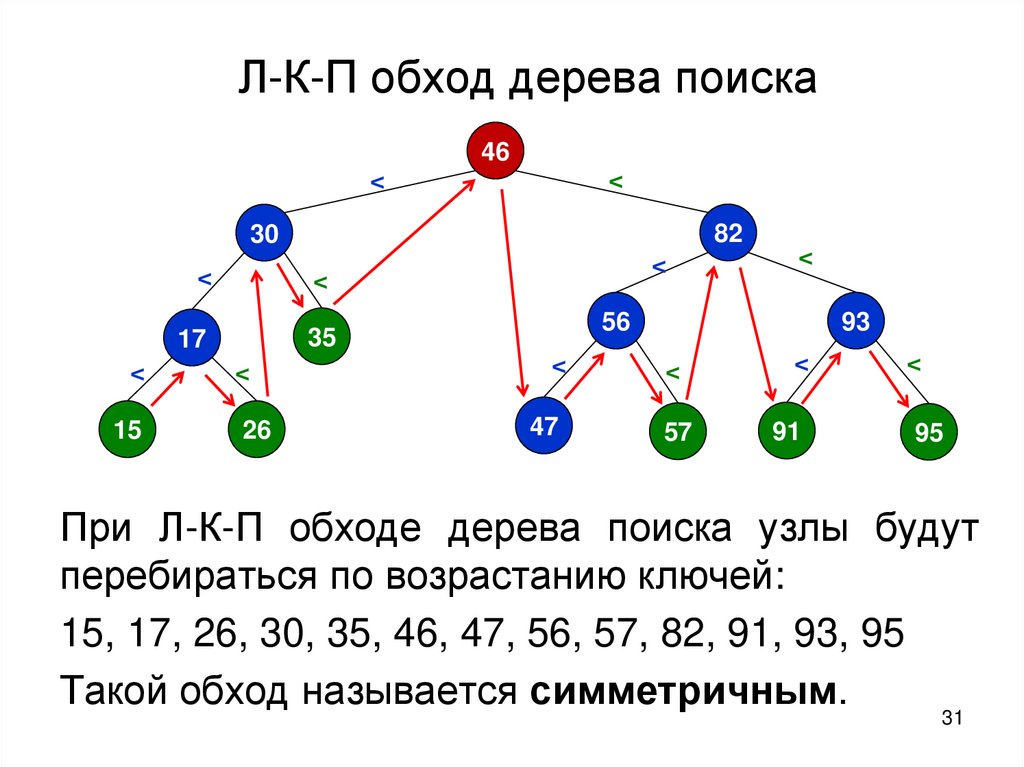
31.

Л-К-П обход дерева поиска
46
<
<
82
30
<
<
17
35
<
<
56
93
<
<
<
<
<
<
15
26
47
57
91
95
При Л-К-П обходе дерева поиска узлы будут
перебираться по возрастанию ключей:
15, 17, 26, 30, 35, 46, 47, 56, 57, 82, 91, 93, 95
Такой обход называется симметричным.
31

32.

Л-К-П обход дерева поиска
//Пример реализации обхода
//Вместо вывода в этот раз складываем ключи узлов в вектор
void SearchTree::lnrKeys(Node *root, std::vector<int> &keys) const
{
if (!root) {
return;
}
lnrPrint(root->leftChild());
keys->push_back(root->key());
lnrPrint(root->rightChild());
}
32

33.

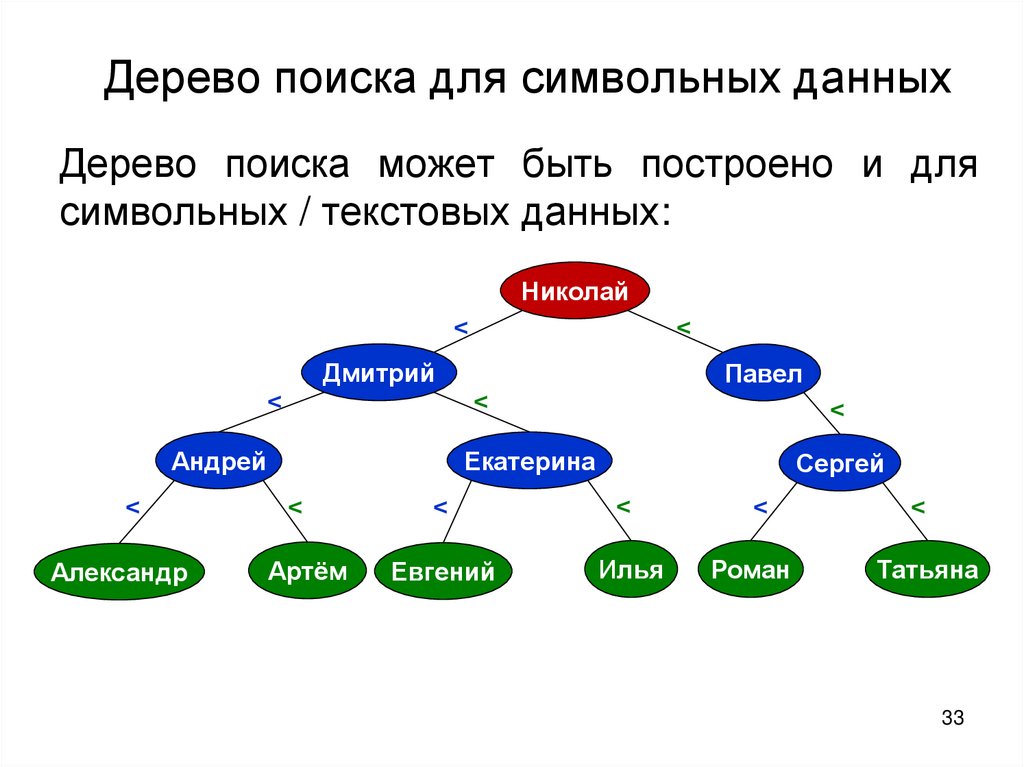
Дерево поиска для символьных данных
Дерево поиска может быть построено и для
символьных / текстовых данных:
Николай
<
<
Дмитрий
<
Павел
<
Андрей
<
Екатерина
Сергей
<
<
<
<
<
<
Александр
Артём
Евгений
Илья
Роман
Татьяна
33

34.

Заключение
Двоичное дерево поиска может быть использовано как
способ такой организации данных, при котором поиск
выполняется по достаточно простому алгоритму.
Причём число сравнений при поиске равно номеру
уровня, на котором находится искомый элемент. Чем
меньше высота дерева, тем меньше уровней. В
идеальном дереве уровней O(log2n) и, следовательно,
поиск в нём сравним с бинарным поиском. В следующих
темах
будет
рассмотрен
метод
построения
сбалансированного
дерева,
которое
близко
к
идеальному.
При необходимости обход дерева может быть
использован для получения упорядоченного массива
34
данных, как было показано выше.